重庆西南师大附中2009届高三数学2月月考试题(文).doc

西南师大附中高2018级上期第二次月考数学试题（文）（2018年11月）（满分：150分 时间：120分钟）第I 卷 （共74分）一、选择题（每小题5分，共50分）1． 已知集合2{|4}M x x =<，2{|230}N x x x =--<，则集合M N =I （ ） A ．{|2}x x <- B ．{|3}x x >C ．{|12}x x -<<D ．{|23}x x <<2． 函数1(5)5y x x =≠-+的反函数是（ ） A ．15(0)y x x =-≠ B ．5()y x x R =+∈C ．15(0)y x x=+≠ D ．5()y x x R =-∈3． 已知函数y = tan ( 2x +ϕ)的图象过点（12π，0），则ϕ的值可以是（ ） A ．6π-B ．6π C ．12π-D ．12π4． 若函数()sin ()f x x ωϕ=+的图象如图，则ωϕ和的取值是（ ）A ．1ω=，3πϕ=B ．1ω=，3πϕ=-C ．12ω=，6πϕ= D ．12ω=，6πϕ=-5． 函数122log (2log )y x =-的值域是（-∞，0），则它的定义域是（ ）A ．（-∞，2）B ．（0，2）C ．（0，4）D ．（2，4）6． 已知4cos 5α=，(,0)2πα∈-，则tan 2α的值是（ ）A ．247-B ．247C ．2425D ．724-7． 将函数sin ()3y x π=-的图象上所有点的横坐标伸长为原来的2倍，纵坐标不变，再将所得图象向左平移3π个单位，得到的图象的解析式为（ ） A ．1sin 2y x = B ．1sin ()22y x π=-C ．1sin ()26y x π=-D ．sin (2)6y x π=-8． 已知数列{a n }，如121321,,,,n n a a a a a a a ----L 是首项为1，公比为2的等比数列，那么a n 等于（ ）A ．121n +-B ．21n -C ．12n -D ．21n +9． 定义在R 上的函数f (x )既是偶函数，又是周期函数，若f (x )的最小正周期为π，且当[0,]2x π∈时，f (x ) = sin x ，则5()3f π的值为（ ）A ．12-B ．12C．D10． 函数2()2sin sin 21f x x x =-++，给出下列四个命题：（1）在区间5[,]88ππ上是减函数；（2）直线8x π=是其图象的一条对称轴；（3）函数f (x )的图象可由函数2y x 的图象向左平移4π而得到； （4）若[0,]2x π∈，则f (x )的值域是[0,其中正确命题是（ ） A ．（1）（3）B ．（1）（2）C ．（3）（4）D ．（1）（4）二、填空题（每小题4分，共24分）11． 求值sin315sin(480)cos(330)︒︒︒--+-=_________________．12．已知tan θ=，则22sin sin cos 2cos θθθθ-+=_________________． 13．函数()cos )cos f x x x x =-的值域是_________________．14． 在等差数列{a n }中，满足3a 4 = 7a 7，且a 1 > 0，S n 是数列{a n }的前n 项和，若S n 取最大值，则n = _________________． 15． 数列{a n }中，a 1 = 1，214a =，且1(1)n n nn a a n a +-=-（n ≥2），归纳前四项特点，写出它的一个通项公式a n = _________________．16． 关于x 的方程22210x x a a +++=g 有实根，则实数a 的取值范围是_________________．西南师大附中高2018级上期第二次月考数学试题参考答案（文）一、选择题（每小题5分，共50分）1．C 2．A 3．A 4．C 5．B 6．A 7．C 8．B 9．D 10．B 二、填空题（每小题4分，共24分） 111213．[31,22-]14．15．132n - 16．(,2⎤-∞-⎦三、解答题（共76分）17．解：原式2(sin cos )(sin cos )222sin cos 2cos 2cos (sin cos )αααααααααα++==++ ∵ α为第二象限角且sin α=∴ 1sin cos 0cos 4ααα+≠=-且∴原式== 18．解：（1）由题意：11195,4421a d a d a d +=⎧⇒==⎨+=⎩ ∴ 41n a n =+（2）由41n a n =+，得412n n b +=∴ 51{}2n b b =是，公比42q =的等比数列∴ 54442(21)32(21)2115n n n S --==-19．解：（1）由312001111x x x x x x +--≥⇔≥⇔<-≥++或 即[)(,1)1,A =-∞-+∞（2）(1)(2)0(1)(2)0x a a x x a x a --->⇔---<∵ a < 1∴ a + 1 > 2a∴ B =（2a ，a + 1） ∵ B A ⊆∴ 2111a a ≥+≤-或即122a a ≥≤-或而a < 1 ∴1122a a ≤<≤-或 故当B A ⊆时，a 的取值范围是1(,2),12⎡⎫-∞-⎪⎢⎣⎭20．解：（1）由111111(1)(1)33S a a a =-⇒=-∴ 112a =-又121222111(1)(1)334S a a a a a =-⇒+=-⇒=（2）当2n ≥时111111(1)(1)311233n n n n n n n n n n a S S a a a a a a a ----=-=---⇒=--+⇒=-∴112n n a a -=- ∴ {}n a 是首项为12-，公比为12-的等比数列且1111()()222nn n a -=--=-21．解：()cos2212sin (2)16f x x x a x a π=++=+++（1）∵ 02x π≤≤∴72666x πππ≤+≤∴ 12sin (2)26x π-≤+≤∴ f (x )最大值、最小值分别为a + 3和a（2）要|()|2f x <，只需232a a >-⎧⎨+<⎩解得21a -<<-22．解：由3cos ()45πα-=3(cos sin )5αα+=cos sin αα+=①①2：1812cos sin 25αα+=7sin 22cos sin 25ααα==- ∴ 2732(cos sin )1()2525αα-=--= 由732cos sin 02522ππααα=-<-<<-及 知32παπ-<<- ∴ cos 0α<，sin 0α>∴ cos sin αα-= ② ①×②得：24cos225α=-cos (2)(cos 2sin 2)4πααα-=+=。

重庆市西南师大附中高2009级第一次月考数 学 试 题（文）2008年9月本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．卷面共150分，考试时间120分钟．第Ⅰ卷 （选择题 共60分）一、选择题：本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设f x x →：是集合A 到集合B 的映射．若{}2,0,2A =-，则A B =A ．{0}B ．{2}C ．{0，2}D ．{2-，0}2．设221(2)()11()2x f f x x f -==+，则A ．– 1B ．1C ．35-D ．353．已知函数1()13(10)x f x f --=+=，则A ．2B ．– 2C ．3D ．– 14．奇函数()[37]f x 在，上是增函数，在[3，6]上的最大值为8，最小值为– 1，则2(6)(3)f f -+-等于A ．5B ．– 5C ．–13D ．– 155．若一系列函数的解析式相同，值域相同，但定义域不同，称这些函数为——同族函数．那么，函数的解析式为2x y =，值域为{4，9}的同族函数共有A ．7个B ．8个C ．9个D ．10个6．命题p ：若a b R ∈，，则1a b +>是1a b +>的充分不必要条件；命题q：函数y =的定义域是(][),13,-∞-+∞ ，则A ．―p 或q ‖为假B ．―p 且q ‖为真C ．p 真q 假D ．p 假q 真7．函数()f x =A ．[]24， B．[0，C．[2， D ．[48]，8．关于x 的函数y =log 21（a 2－ax +2a ）在［1，+∞)上为减函数，则实数a 的取值范围是A ．（-∞，0）B ．（1-，0）C ．（0，2]D ．（－∞，－1）9．若f （x ）是偶函数，且当x ∈［0，+∞)时，f （x ） = x – 1，则不等式f （x －1） >1的解集是A ．{x |1-< x < 3}B ．{x | x <1-，或x >3}C ．{x | x > 2}D ．{x | x > 3}10．已知函数()y f x =是偶函数，()y g x =是奇函数，它们的定义域为[]ππ-，，且它们在[0]x π∈，上的图象如下图所示，则不等式()()f xg x ＞0的解集为 A ．(0)()33πππ- ，，B ．()(0)33πππ-- ，，C ．(0)()44πππ- ，，D ．()()33ππππ--，， 11．已知()f x 是定义在R 上的偶函数，并且满足1(2)()f x f x +=-，当23x ≤≤时，()21f x x =-，则(5.5)f 等于A ．10B ．– 4C ．3D ．412．若关于x 的方程21(1)10(01)x xa a a a m+++=>≠，有解，则m 的取值范围是A ．1[0)3-，B ．1[0)(01]3- ，，C ．1(]3-∞-，D ．[1)+∞，第II 卷 （共90分）二、填空题：本大题共4小题，每题4分，共16分．13．设函数2()log (3)f x x =+的图像为C 1，函数()y g x =的图像为C 2，若C 1与C 2关于直线y x =对称，则(1)(1)f g +的值为 ．14．设函数1, 0()0, 01, 0x f x x x >⎧⎪==⎨⎪-<⎩，则方程()1(21)f x x x +=-的解集为____________．15．已知命题p ：1122k ->；命题q ：函数22log (2)y x kx k =-+的值域为R ，则p 是q 的___________________条件．16．奇函数()()f x x R ∈满足：(4)0f -=，且在区间[03]，与[)3+∞，上分别递减和递增，则不等式2(4)()0x f x -<的解集为_________________．三、解答题：本题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分12分）已知函数5()3x f x x =-，[()]4f g x x =-．（1）求()g x 的解析式； （2）求1(5)g -的值．18．（本小题满分13分）解下列不等式： （1）|3|2||x x +> （2）22132x x x +≥-+已知()y f x =是定义在R 上的奇函数，当0x ≥时，2()2f x x x =-． （1）求()y f x =的解析式；（2）画出函数()y f x =的图象，并指出()f x 的单调区间及在每个区间上的增减性； （3）若函数()y f x =的定义域为[a ，b ]，值域为11[](1)a b ba ≤<，，求实数a 、b 的值．20．（本小题满分12分）函数()f x 对一切实数x ，y 均有()()(21)f x y f y x y x +-=++成立，且(1)0f =． （1）求(0)f 的值；（2）当()32f x x a +<+在1(0)2，上恒成立时，求a 的取值范围．已知二次函数2()f x ax bx c =++和一次函数()g x bx =-，其中实数a 、b 、c 满足a b c a b c >>++=，．（1）求证：两函数的图象交于不同的两点A 、B ； （2）求线段AB 在x 轴上的射影A 1B 1的长的取值范围．22．（本小题满分12分）已知()f x 是定义在［－1，1］上的奇函数，且(1)1f =，若[11]a b ∈-，，，0a b +≠时，有()()0f a f b a b+>+．（1）判断函数()f x 在［－1，1］上是增函数，还是减函数，并证明你的结论； （2）解不等式：11()()21f x f x +<-；（3）若2()21f x m pm ≤-+对所有[11]x ∈-，，[11]p ∈-，（p 是常数）恒成立，求实数m 的取值范围．西南师大附中高2009级第一次月考数学试题参考答案（文）一、选择题：本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．C 2．A 3．B 4．D 5．C 6．D 7．C 8．D 9．B 10．B 11．D 12．A 二、填空题：本大题共4小题，每题4分，共16分． 13．114．{0，2，4}15．充分不必要16．(4)(20)(24)-∞-- ，，，三、解答题：本题共6小题，共74分． 17．解：（1）∵5()3x f x x =-，∴[()]f g x 5()()3g x g x =- 3分又[()]4f g x x =-，∴5()4()3g x xg x =--，解得312()1x g x x -=+ 6分（2）∵反函数的自变量就是原函数的函数值 9分∴在312()1x g x x -=+中有31251x x -=+，解得172x =-，∴117(5)2g -=-12分18．解：（1）原不等式等价于 22(3)4x x +> 2分即 2230x x --< 4分 解得 13x -<< 5分∴ 原不等式的解集为{|13}x x -<< 6分 （2）原不等式等价于221032x x x +-≥-+224032x x x x -⇔≤-+ 2分(4)0(1)(2)x x x x -⇔≤-- 4分解得 0124x x ≤<<≤或∴ 原不等式的解集为{|0124}x x x ≤<<≤或 7分19．解：（1）当x < 0时，– x > 0，∴ 22()()[2()()]2f x f x x x x x =--=----=+2分∴ ()f x 的解析式为 222(0)()2(0)x x x f x x x x ⎧-≥⎪=⎨+<⎪⎩ 4分蓝天家教网 伴你快乐成长（3）∵ ()f x 在[1)+∞，上是减函数，且1a b ≤<，∴()f x 在[a ，b ]上是减函数 ∴ 1()1()f a a f b b⎧=⎪⎪⎨⎪=⎪⎩10分即221212a a a b b b ⎧-=⎪⎪⎨⎪-=⎪⎩12分22(1)(1)0(1)(1)0a a ab b b ⎧---=⎪⇔⎨---=⎪⎩，解得 1212a ab b ⎧==⎪⎪⎨⎪==⎪⎩或或∵ 1a b ≤<，∴ 12a b =⎧⎪⎨=⎪⎩13分20．解：（1）令x = 1，y = 0得(1)(0)2f f -= 2分∵ (1)0f =，∴ (0)2f =- 4分（2）在()()(21)f x y f y x y x +-=++中，令y = 0 得()(0)(1)f x f x x -=+∴ 2()2f x x x =+-6分∴ 不等式1()32(0)2f x x a +<+在，上恒成立21a x x ⇔>-+在（0，12）上恒成立设21()1(0)2g x x x x =-+∈，，，则只需max ()a g x ≥ 10分∵213()()24g x x =-+在（0，12）上是减函数，∴max ()(0)1g x g ==∴ a 的取值范围是1a ≥12分21．（1）证明：联立2y ax bx cy bx ⎧=++⎨=-⎩消去y 得220ax bx c ++= （*） 2分∵ 22444()b ac b ac ∆=-=-，由000a b c a b c a c >>++=><，知，，∴0ac <蓝天家教网 伴你快乐成长∴0∆>，从而方程（*）有两个不等实根， 即两函数的图象交于不同的两点6分（2）设方程（*）的两根为x 1，x 2，则12122b c x x x x aa+=-=，∴ 222221112121222444||()()4()b c b acA B x x x x x x aaa-=-=+-=--=22224()4134[()()1]4[()]24a c acc c c aa a a ---==++=++∵a b a c c >=-->，∴ 22a c a c >-->，，∴ 122c a -<<-，∴ 31022a c-<+<∴2190()24ca<+<，∴2113||12A B <<11A B <<即AB 在x 轴上的射影A 1B 112分22．解：（1）函数()f x 在［– 1，1］上是增函数设1211x x -≤<≤∵()f x 是定义在［–1，1］上的奇函数，∴ f （x 2）－f （x 1 ）= f （x 2 ）+ f （– x 1）． 又x 1 < x 2，∴ x 2 +（– x 1）≠0，由题设有2121()()()f x f x x x +-+-＞0，∵ x 2 +（– x 1）= x 2－x 1>0，∴ f （x 2 ）+ f （– x 1）>0，即f （x 1 ）< f （x 2 ）， 所以函数f （x ） 在［– 1，1］上是增函数． 4分（2）不等式11()()21f x f x +<-1311122211120131111221x x x x x x x x x ⎧-≤+≤⎧⎪-≤≤⎪⎪⎪⎪⎪⇔-≤≤⇔≥≤⎨⎨-⎪⎪⎪⎪<-<<+<⎪⎪⎩-⎩或或312x -≤<-解得 8分（3）由（1）知max ()(1)1f x f ==，∴ 2()21[11]f x m pm x ≤-+∈-对任意，恒成立只需2121[11]m pm p ≤-+∈-对，恒成立，即 220[11]m pm p -≥∈-对，恒成立设222(1)020()2220(1)020g m m g p m m p m m m g m m ⎧-≥+≥⎧⎪=-≤-≥=⎨⎨≥-≥⎪⎩⎩，则解得或或 ∴ m 的取值范围是(2][2){0}-∞-+∞ ，， 12分。

2009届重庆市西南师大附中高三第三次月考数学试卷（理）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．共150分，考试时间120分钟．第Ⅰ卷（选择题共50分）一、选择题：本大题共10小题，每题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知向量(82)(1)a b x==，，，，若//a b，则x的值为（）A．14B．14-C．4 D．– 42.两圆32cos3cos42sin3sinx xy yθθθθ=-+=⎧⎧⎨⎨=+=⎩⎩与的位置关系是（）A．内切B．外切C．相离D．内含3.“a = 3”是“直线210ax y--=与直线640x y c-+=平行”的（）条件A．充要B．充分而不必要C．必要而不充分D．既不充分也不必要4.已知直线l1：122y x=+，l2过点P（– 3，1），且l1到l2的角为45︒，则l2的方程为（）A．3100x y++=B．3100x y-+=C．20x y++=D．30x y+=5.已知23()1xf xx+=-，函数()y g x=的图象与函数1(1)y f x-=+的图象关于直线y x=对称，则(11)g等于（）A．32B．52C．2711D．2396.已知点P（x，y）是直线kx + y + 4 = 0（k > 0）上一动点，P A、PB是圆C：2220x y y+-=的两条切线，A、B是切点，若四边形P ACB的最小面积是2，则k的值为（）A．3 B C．D．27.已知4a b ab+=，a、b均为正数，则使a b m+>恒成立的m的取值范围是（）A．m < 9 B．9m≤C．m < 8 D．8m≤8.已知{}n a为等差数列，若11101a a <-，且它的前n项和nS有最大值，那么当nS取得最小正值时，n =（ ）A ．11B ．20C ．19D ．219.已知O 是△ABC 内一点，230OA OB OC ++=，则△AOC 与△BOC 的面积的比值为（ ）A ．32B ．53C ．2D ．310.把数列{21n +}依次按第一个括号一个数，第二个括号两个数，第三个括号三个数，第四个括号四个数，第五个括号一个数，第六个括号两个数，…循环分别为（3），（5，7），（9，11，13），（15，17，19，21），（23），（25，27），（29，31，33），（35，37，39，41），（43） （45，47）…则第104个括号内各数之和为（ ）A ．2036B ．2048C ．2060D ．2072第II 卷 （共100分）二、填空题：本大题共6小题，每题4分，共24分．11.若cos 2sin 4απα=⎛⎫- ⎪⎝⎭，则cos sin αα+的值为____________． 12.等差数列{}n a 的前n 项和为n S ，若31815618S S S =--=，，则18S =____________．13.如图，某地一天从6时到14时的温度变化曲线近似满足函数sin()(02)y A x B ωϕϕπ=++≤<，则温度变化曲线的函数解析式为____________．14.已知函数2|1|(0)()1(0)x x f x x x -+≤⎧=⎨->⎩．那么不等式()0f x <的解集为_______________． 15.x 、y 满足约束条件：225040y x y x y ≥⎧⎪+-≥⎨⎪+-≤⎩，则|5|z x y =+-的最小值是______________．16对于函数f ( x ) = x | x | + px + q ，现给出四个命题：① q = 0时，f ( x )为奇函数② y = f ( x )的图象关于（0，q ）对称③ p = 0，q > 0时，方程f ( x ) = 0有且只有一个实数根④方程f ( x ) = 0至多有两个实数根其中正确命题的序号为_____________________．三、解答题：本题共6小题，共76分，解答应写出文字说明、证明过程或演算步骤．17.(本小题满分12分) 已知2)(),cos 2,(sin ),cos ,cos 35(b b a x f x x b x x a +===记函数(1) 求函数f ( x )的最小正周期；(2) 当62x ππ≤≤时，求函数f ( x )的值域．18.(本小题满分12分) 已知2(1)()(0)2x p x p f x p x p+++=>+ （1）若p > 1时，解关于x 的不等式()0f x ≥；（2）若()2f x >对24x ≤≤时恒成立，求p 的范围．19.(本小题满分12分) 数列{a n }中，a 1 = 1，当2n ≥时，其前n 项和满足21()2n n n S a S =- （1）求S n 的表达式；（2）设21n n S b n =+，数列{b n }的前n 项和为T n ，求T n ． 20.(本小题满分14分) 已知圆C 经过P （4，– 2），Q （– 1，3）两点，且在y 轴上截得的线段长为，半径小于5．（1）求直线PQ 与圆C 的方程．（2）若直线l ∥PQ ，且l 与圆C 交于点A 、B ，90AOB ∠=︒，求直线l 的方程．21.(本小题满分12分) 已知函数1()|1|(0)f x x x=->， . （1）当0 < a < b ，且f ( a ) = f ( b )时，求证：ab >1；（2）若存在实数a ，b （a < b ），使得函数()y f x =的定义域为 [a ，b ]时，值域为[]ma mb ，(0m ≠)，求m 的取值范围．22.(本小题满分14分) 数轴上有一列点P 1，P 2，P 3，…，P n ，…，已知当2n ≥时，点P n 是把线段P n – 1 P n +1作n 等分的分点中最靠近P n+1的点，设线段P 1P 2，P 2P 3，…，P n P n + 1的长度分别为a 1，a 2，a 3，…，a n ，其中a 1 = 1．（1）写出a 2，a 3和a n （2n ≥，*n N ∈）的表达式；（2）证明a 1 + a 2 + a 3 +…+a n < 3（*n N ∈）；（3）设点M n ( n ，a n )（n > 2，*n N ∈），在这些点中是否存在两个点同时在函数2(0)(1)k y k x =>-的图像上，如果存在，请求出点的坐标；如果不存在，请说明理由．。

重庆市西南师大附中高2009级第四次月考语文试题第Ⅰ卷（共30分）一．（12分，每小题3分）1．选出下列加点字读音全对的一项A．气馁（lěi）寥落（liáo）阴谋秘计（bì）殒身不恤（yǔn）B．憋闷（biē）摒除（bǐng）吊民伐罪（fǎ）溘然长逝（hé）C．靛蓝（dìng）玷辱（diàn）摧山坼地（tuó）封妻荫子（yìn）D．敧侧（qī）翎毛（líng）重蹈覆辙（fù）甘之如饴（yí）2．选出有两个错别字的一项A．坦护规距不堪忍受无耻澜言B．眩耀熟练题纲挈领风尘仆仆C．防碍姑息优柔寡断侥幸过关D．污告掩饰杳无音信同仇敌忾3．下列各句中加线的熟语．成语使用不恰当的一句是A．这个人很讲义气，与朋友交往总是言必信，行必果，大家都非常佩服他。

B．干事情要讲求效率，如果一不做，二不休，整天熬天混日，是很难创出佳绩来的。

C．我现在决定不再办理工作调动手续了，俗话说，一动不如一静，还是留在这里吧。

D．赵教授在这次研究院学术会议上的发言精彩之极，真所谓不刊之论。

4．下列各句中，没有语病的一句是A．年轻人一定要从中华民族伟大复兴的历史高度，充分认识学习社会科学．提高民族素质的重要意义很有必要。

B．“楼船夜雪瓜洲渡，铁马秋风大散关”这两句诗虽然只选取了几个名词，但并不影响意义的完整表达，语言凝炼，意境开阔。

C．近年来，国外教育机构不仅在寻求与我国包括民办高校在内的各类学校合作，而且许多人也开始将注意力投向民办教育。

D．四月份以来，娄底和郴州接连发生了两起矿山安全事故，省委．省政府及时成立了调查组，调查事故发生的原因并寻求防止类似事故不再发生的办法。

二．（9分，每小题3分）阅读下面的文字，完成7—10题。

绿色建筑回顾人类建筑发展的历史，从远古时代到工业革命之前，其外部．内部的装饰及造型，反映了人类的艺术甚至是哲学思想的历程，但就其内部的居住环境而言，它仅仅是遮风避雨的“掩蔽所”。

西南师大附中高2010级第四次月考数 学 试 题（文）2009年12月（满分：150分 时间：120分钟）一、选择题（每小题5分，共50分）1． 设A ={(x ,y )|x –y =6}，B ={(x ,y )|3x +2y =7}，满足C A B ⊆的集合C 的个数为（ ）A ．0B ．1C ．2D ．42． 已知a =（– 2，1），b =（– 1，2），而（λa +b ）⊥（a –λb ），则λ等于（ ）A ．1或2B ．2或21-C ．1或 – 1D ．– 1或2 3． 直线260ax y ++=与直线2(1)(1)0x a y a +-+-=平行，则a 等于（ ）A ．－1或2B ．2C ．－1D ．234． 若110a b<<，则下列结论不正确的是（ ） A ．22a b <B ．2ab b <C ．2b aa b+>D ．||||||a b a b +>+ 5． 不等式2821()33x x -->的解集是（ ）A ．（–2，4）B ．（-∞，– 2）C ．（4，+∞）D ．（-∞，– 2）（4，+∞）6． 可行域A ：10400,0x y x y x y -+≥⎧⎪+-≤⎨⎪≥≥⎩与可行域B ：04502x y ≤≤⎧⎪⎨≤≤⎪⎩的关系是（ ）A ．A ⊆B B ．B ⊆AC ．B AD ．A B7． 直线l 在x 轴与y 轴上的截距相等，且点P （3，4）到直线l 的距离恰好为4，则满足条件的直线有（ ）A ．1条B ．4条C ．2条D ．3条 8． 已知当R x ∈时，函数()y f x =满足1(2.5)(1.5)3f x f x +=++，且4(1)3f =，则(2010)f 的值为（ ） A ．20103B ．20143C ．671D ．2689． 三个实数x 、y 、z 成等比数列，若x+y+z=1成立，则y 取值X 围是（ ）A ．[31，+∞) (-∞，– 1 ] B ．[–1，0) ( 0，31] C ．[–31，0] D ．[–31，0) ( 0，1]10． 设S 是ABC ∆的面积，角A 、B 、C 的对边分别为a 、b 、c ，且2sin ()sin S A BA BC B <，则（ ）A ．ABC ∆是钝角三角形B ．ABC ∆是锐角三角形C ．ABC ∆可能为钝角三角形，也可能为锐角三角形D ．无法判断二、填空题（每小题5分，共25分）11．不等式(0x -的解集为______________． 12． 已知函数2())2sin ()()612f x x x x R ππ-+-∈，则函数()f x 的最小正周期为________________．13． ABC ∆的三内角A 、B 、C 所对边的长分别为a 、b 、c ，设向量(,)p a c b =+，(,)q b a c a =--,若//p q ，则角C 的大小为．14． 设x ，y ，z 满足约束条件组1010232x y z x y x z ++=⎧⎪⎪≤≤⎪⎨≤≤⎪⎪⎪+≤⎩则t= 5x +6y +4z 的最大值为．15． 过△ABO 的重心G 的直线与OA 、OB 两边分别交于P 、Q 两点，且此直线不与AB 边平行，设OP =m OA ，OQ =n OB ，求11m n +的值．三、解答题（共75分）16． (12分) 在△ABC 中，｜AB ｜＝｜AC ｜，∠A ＝120°，A （0，2），BC 所在直线方程为3 x －y －1＝0，求边AB 、AC 所在直线方程．17． (12分) 已知向量a 与b 的夹角为30°，且|a ||b |＝1，(1) 求|a －2b |的值；(2) 设向量p ＝a ＋2b ，q ＝a －2b ，求向量p 在q 方向上的投影．18． (12分) 已知m R ∈，2 (1, )a x m =-+，1 (1, )b m x =+， (, )x c m x m=-+．(1) 当1m =-时，求使不等式 1a c ⋅<成立的x 的取值X 围； (2) 当m ≥1时，求使不等式 0a b ⋅>成立的x 的取值X 围．19． (13分)已知函数x x f =)(，a x x g +=)(（a > 0）(1) 求a 的值，使点M （)(x f , )(x g ）到直线01=-+y x 的最短距离为2； (2) 若不等式1)()()(≤-x f x ag x f 在x ∈[1，4]恒成立，求a 的取值X 围．20． (13分) 已知点A ，B 的坐标分别是（0，–1），（0，1），直线AM ，BM 相交于点M ，且它们的斜率之积为12-．(1) 求点M 的轨迹C 的方程；(2) 过D （2，0）的直线l 与轨迹C 有两个不同的交点时，求l 的斜率的取值X 围；(3) 若过D （2，0）的直线l 与(1)中的轨迹C 交于不同的E 、F （E 在D 、F 之间），求ODE ∆与ODF ∆的面积之比．21． (13分) 已知曲线C ：2()n f x x A A =上的点、的横坐标分别为1和(123)n a n =，，，，且a 1=5，数列{x n }满足x n +1=tf (x n –1) +1（t>0且112t t ≠≠,）．设区间[1,](1)n n n D a a =>，当n nx D ∈时，曲线C 上存在点(())n n n P x f x ，使得x n 的值与直线AA n 的斜率之半相等．(1) 证明：{1log (1)}t n x +-是等比数列；(2) 当1n D +n D 对一切*n N ∈恒成立时，求t 的取值X 围；(3) 记数列{a n }的前n 项和为S n ，当14t =时，试比较S n 与n +7的大小，并证明你的结论． 西南师大附中高2010级第四次月考数学试题参考答案（文）2009年12月一、选择题（每小题5分，共50分）1．C 2．C 3．C 4．D 5．A 6．D 7．B 8．C 9．B 10．A 二、填空题（每小题5分，共25分） 11．{5}[3,)-+∞ 12．π 13．3π14．9 15．3 三、解答题（共75分）16．解：由题意得∠B ＝∠C ＝30°，设AB 边斜率的夹角公式得＝ 33从而得k = 33 ·········································································································· 10分 又AB 斜率不存在时也适合题意∴AB 边所在直线方程为y ＝ 33 x+2和x ＝0. ····················································· 12分17、解：(1) ∵|a －2b ==233443⨯⨯-+=1 ···· 6分 (2) 法一：由（1）可知21q a b =-=；2(2)13p a b =+=2241p q a b ⋅=-=- ∴><q p ,cos =p q p q⋅⋅=1313-从而在方向上的投影为cos ,1p p q <>=- ······················································· 12分 （法二）：∵由（1）可知21q a b =-=；cos ,p p q <>=p q p p q⋅⋅⋅=1p q ⋅=-18．解：(1) 当1m =-时，2(1, 1)a x =--， (1, )1x c x =-.2(1) 11x x a c x -⋅=-+-21x x =+-. ∵ 2 11a c x x ⋅=+-<,∴ 2211,1 1.x x x x ⎧+->-⎪⎨+-<⎪⎩ 解得 21x -<<-或01x <<.∴ 当1m =-时，使不等式 1a c ⋅<成立的x 的取值X 围是{}2101x x x -<<-<<或. ···················································································· 6分(2) 当m ＝1时，(0, 1 )(1, )x ∈+∞当m >1时，(0, 1 )(, )x m ∈+∞. ····················································································· 12分19．解：(1) 由题意得M 到直线01=-+y x 的距离2|1|-++=a x x d ，令0≥=x t则2|45)21(|2|1|22-++==++=a t a t t d ∵0≥t∴1≥a215|()|t a ++-≥即t = 0时，221min =-=a d ∴a = 3 10<<a 时，0min =d ，不合题意综上3=a ·········································································································· 6分 （2）由2)()(01)()()(11)()()(≤≤⇔≤-≤-⇔≤-x f x ag x f x ag x f x f x ag x f即]4,1[22在≤+xa ax 上恒成立也就是x a ax 22≤+在 [1，4] 上恒成立 令0≥=t x ，且2t x =，]2,1[∈t 由题意0222≤+-a t at 在]2,1[∈t 上恒成立 设222)(a t at t +-=ϕ，则要使上述条件成立，只需)12(20044)2(02)1(22-≤<⇒⎪⎩⎪⎨⎧≤-+=≤+-=a a a a a ϕϕ 即满足条件的a 的取值X 围是]222,0(- ················································ 13分20．解：(1) 设点M 的坐标为(,)x y ，∵12AM BM k k ⋅=-，∴0x ≠），这就是动点M 的轨迹方程．······················4分 (2) 由题意知直线l 的斜率存在，设l 的方程为()2y k x =-（12k ≠±）① 将①代入1222=+y x ，得0)28(8)12(2222=-+⋅-+k x k x k （*） 由0∆>，解得11112()(,)(,)222222k ∈---． ······································8分(3) 设11(,)E x y ，22(,)F x y ，由222)12y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩，消x 得：281450x x -+=∴112x =，254x = 令||||ODE ODF S DE S DF λ∆∆==DE DF λ= ∴122122x x λλ-==-= 1∶2 ·········································································· 13分21．解：(1) ∵由已知得∴2112, 1.12n n n n n a a x x a -+==>-即 由211)1(1,1)1(-=-+-=++n n n n x t x x tf x 得∴),1(log 21)1(log 1-+=-+n t n t x x 即].1)1([log 21)1(log 1+-=+-+n t n t x x ∴}1)1({log +-n t x 是首项为t log 2+1为首项，公比为2的等比数列. ······ 4分(2) 由(1)得1)1(log +-n t x =（t log 2+1）·2n-1，∴1211(2)n n x t t-=+从而a n =2x n －1=1+12)2(2-n t t ，由D n+1D n ，得a n+1<a n ，即122(2)(2)n n t t -<. ∴0<2t <1，即0<t <.219分(3) 当41=t 时，12118()2n n a -=+∴])21()21()21(21[81242-+++++=n n S n不难证明：当n≤3时，2n-1≤n+1；当n≥4时，2n-1>n+1.∴当n≤3时，;7213])21()21(21[842+<+=+++≤n n n S n 当n≥4时，])21()21()21()21()21(21[816542+++++++<n n n S.7)21(72+<-+=-n n n综上所述，对任意的.7*,+<∈n S N n n 都有13分。

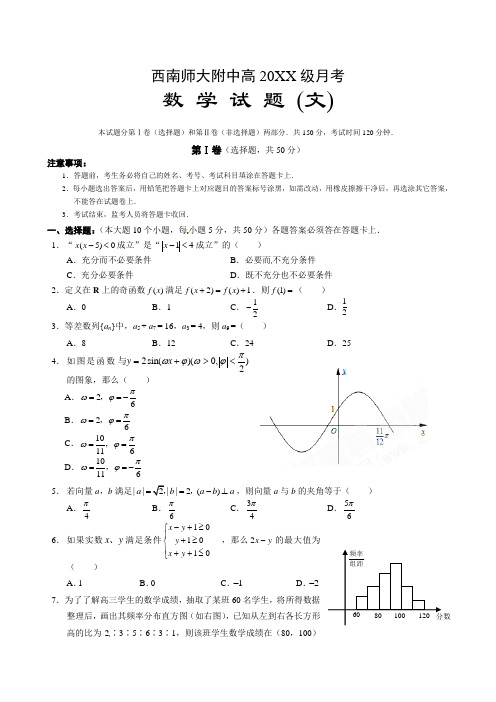
西南师大附中高20XX 级月考数 学 试 题 (文)本试题分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．共150分，考试时间120分钟．第Ⅰ卷（选择题，共50分）注意事项：1．答题前，考生务必将自己的姓名、考号、考试科目填涂在答题卡上．2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案，不能答在试题卷上．3．考试结束，监考人员将答题卡收回．一、选择题：（本大题10个小题，每小题5分，共50分）各题答案必须答在答题卡上．1．“(5)0x x -<成立”是“14x -<成立”的（ ） A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件2．定义在R 上的奇函数()f x 满足(2)()1f x f x +=+．则(1)f =（ ）A ．0B ．1C ．12- D ．12 3．等差数列{a n }中，a 5 + a 7 = 16，a 3 = 4，则a 9 =（ ）A ．8B ．12C ．24D ．254． 如图是函数)2,0)(sin(2πϕωϕω<>+=x y 与的图象，那么（ ）A ．26πωϕ==-，B ．26πωϕ==，C ．10116πωϕ==，D ．10116πωϕ==-， 5． 若向量a ，b 满足||2||2()a b a b a ==-⊥，，，则向量a 与b 的夹角等于（ ）A ．4πB ．6πC ．34πD ．56π 6． 如果实数x y 、满足条件101010x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩，那么2x y -的最大值为（ ）A ．1B ．0C ．1-D ．2-7．为了了解高三学生的数学成绩，抽取了某班60名学生，将所得数据整理后，画出其频率分布直方图（如右图），已知从左到右各长方形高的比为2∶3∶5∶6∶3∶1，则该班学生数学成绩在（80，100） 100 120 60 80 分数 组距频率之间的学生人数是（ ）A ．32人B ．27人C ．24人D ．33人8．已知函数)0(18),20(cos 4cos ),0(42321>+=<<+=≠+=x x x y x x x y x x x y π )20)(tan 221)(cot 1(4π<<++=x x x y ，其中以4为最小值的函数个数是（ ） A ．0 B ．1 C ．2 D ．3 9．在半径为10cm 的球面上有A ，B ，C 三点，且AB =38cm ，∠ACB =60°，则球心O 到平面ABC 的距离为（ ）A ．2cmB ．4cmC ．6cmD ．8cm10．已知函数()()f x x R ∈满足(1)1f =，且()f x 的导函数1()2f x '<，则1()22x f x <+的解集为（ ） A ．{}11x x -<< B ．{}1x x <- C ．{}11x x x <->或D ．{}1x x >第Ⅱ卷（非选择题，共100分）二、填空题：（本大题5个小题，每小题5分，共25分）各题答案必须填写在答题卡上（只填结果，不要过程）11．设U ={2，3，4，5，6}，2{|680}A x x x =-+=，B ={2，5，6}，则()U C B B =___________．12．在261()x x-的展开式中，常数项为 ． 13．已知21tan()tan()544παββ+=-=，，则cos sin cos sin αααα+-的值为 ． 14．某旅馆有三人间、两人间、单人间三种房间各一间可用，有三个成人带两个小孩来投宿，小孩不宜单住一间(必须有成人陪同)．若三间房都住有人，则不同的安排住宿方法有___________种．15．已知双曲线22221(00)x y a b a b-=>>，的右焦点为F ，若过点F 且倾斜角为60︒的直线与双曲线的右支有且只有一个交点，则此双曲线离心率的取值范围是___________．三、解答题：（本大题6个小题，共75分）各题解答必须答在答题卡上（必须写出必要的文字说明、演算步骤或推理过程）16．(本小题满分13分)已知函数2313()sin cos 2g x x x x =-的图象按向量1()42m π=-，平移得到函数 2()cos ()3f x a x b π=++的图象． (1) 求实数a 、b 的值；(2) 设函数()()3()[0]2x g x x x πϕ=∈，，，求函数()x ϕ的单调递增区间和最值． 17．(本小题满分13分)有A 、B 、C 、D 、E 共5个口袋，每个口袋装有大小和质量均相同的4个红球和2个黑球，现每次从其中一个口袋中摸出3个球，规定：若摸出的3个球恰为2个红球和1个黑球，则称为最佳摸球组合．(1) 求从口袋A 中摸出的3个球为最佳摸球组合的概率；(2) 现从每个口袋中摸出3个球，求恰有3个口袋中摸出的球是最佳摸球组合的概率．18．(本小题满分13分)已知函数()f x 的导数2'()33(0)f x x ax f b =-=，．a ，b 为实数，12a <<．(1) 若()f x 在区间[11]-，上的最小值、最大值分别为2-、1，求a 、b 的值； (2) 在 (1) 的条件下，求曲线在点P （2，1）处的切线方程．19．(本小题满分12分)如图，在四棱锥P —ABC D 中，底面ABCD 是矩形，已知AB = 3，AD =2，P A = 2，22PD =，60PAB ∠=︒．(1) 证明：AD ⊥平面P AB ；(2) 求异面直线PC 与AD 所成的角的大小；(3) 求二面角P —BD —A 的大小．20．(本小题满分12分)设F 是椭圆C ：22221(0)x y a b a b+=>>的左焦点，直线l 为其左准线，直线l 与x 轴交于点P ，线段MN 为椭圆的长轴，已知||8||2||MN PM MF ==，且．(1) 求椭圆C 的标准方程；(2) 若过点P 的直线与椭圆相交于不同两点A 、B 求证：∠AFM =∠BFN ．21．(本小题满分12分)数列{}n a ：满足2112,66().n n n a a a a n N *+==++∈(1) 设5log (3)n n C a =+，求证{}n C 是等比数列；(2) 求数列{}n a 的通项公式；(3) 设21166n n n nb a a a =--+,数列{}n b 的前n 项和为n T ，求证：51.164n T -≤<-西南师大附中高20XX 级月考 数学试题参考答案 (文)审核人：张浩 校对：陈亮20XX 年5月17．解：(1) 从口袋A 中摸出的3个球为最佳摸球组合即为从口袋A 中摸出2个红球和1个黑球，其概率为2142363.5C C P C ⋅== ··············································································· 6分 (2) 由题意知：每个口袋中摸球为最佳组合的概率相同，从5个口袋中摸球可以看成5 次独立重复试验，故所求概率为332532216()()55625P C =⋅⋅= ································································· 13分 18．解：(1) 由已知得，323()2f x x ax b =-+， 由()0f x '=，得10x =，2x a =． ∵[1, 1]x ∈-，12a <<，∴ 当[1, 0)x ∈-时，()0f x '>，()f x 递增；当(0, 1]x ∈时，()0f x '<，()f x 递减．∴ ()f x 在区间[1, 1]-上的最大值为(0)f b =，∴1b =． 又33(1)11222f a a =-+=-，33(1)1122f a a -=--+=-，∴ (1)(1)f f -<．由题意得(1)2f -=-，即322a -=-，得43a =． 故43a =，1b =为所求． (2) 由 (1) 得32()21f x x x =-+，2()34f x x x '=-，点(2, 1)P 在曲线()f x 上．20．解：(1) ∵ ||8MN = ∴ a = 4又∵ | PM | = 2 | MF |得212()23101()32a a a c e e e e -=--+=⇒==即或舍去 122)(1210132)(2||2||22222=-==∴==⇒=+--==c a b c e c e e c a a ca MF PM 舍去或即得又1121622=+∴y x 椭圆的标准方程为 ········································································· 6分 (2) 当AB 的斜率为0时，显然.0=∠=∠BFN AFM 满足题意当AB 的斜率不为0时，设),(),,(2211y x B y x A ，AB 方程为,8-=my x代入椭圆方程整理得 014448)43(22=+-+my y m 则 431444348),43(1444)48(22122122+=⋅+=++⨯-=∆m y y m m y y m m 662222112211-+-=+++=+∴my y my y x y x y k k BF AF 0)6)(6()(62212121=--+-=my my y y y my .,0BFN AFM k k BF AF ∠=∠=+∴从而 综上可知：恒有BFN AFM ∠=∠ ························································· 12分又221110,591659n <≤=--51.164n T ∴-≤<- ···························· 12分。

西南师大附中高2009级第二次月考西南师大附中高2009级第二次月考语文试题（总分：150分考试时间：150分钟）2009年6月第卷（共30分）一、（每小题3分，共12分）1．下列各组词语中加点的字的读音，全都正确的一组是（）A．伫（zh）立伉（kng）俪慰藉（j）溘（k）然长逝B．窘（jing）迫诅（z）咒熨（y）帖络（1o）腮胡子C．追溯（s）干瘪（bi）蹊（x）跷蹉（cu）跎岁月D．隽（jun）永偌（ru）大确凿（zo）游目骋（chng）怀2．下列各组词语中，没有错别字的一组是（）A．症候坐右铭目不遐接反腐倡廉飞机上开研讨会——高谈阔论B．觉解化妆品质疑思辨融会贯通棒槌里插绣花针——粗中有细C．福祉发烧碟连篇累椟革故鼎新天文台的望远镜——好高骛远D．篇幅渡假村曲高和寡妍媸必露吊扇下面拉家常——讲风凉话3．下列各项中，加点的成语使用恰当的一项是A．在新课改的背景下，这所学校针对学生良莠不齐的现状，在各年级采取分层教育的办法。

实现学生在不同层面的提高。

B．如今图书音像类出版物的热销让出版物的质量再度成为人们的焦点。

但仍有一些出版社对出现的质量问题不置可否，听不进上级部门及广大读者的批评意见。

C．即使恶习已经到了根深蒂固的程度，也还是可以矫正的。

D．刚刚参观了城市远景规划展览的政协委员们在座谈会上高谈阔论，畅所欲言。

表现出参政议政的极大热情。

4．下列各句中没有语病的一句是（）A．对如何以前所未有的全球性行动来帮助受灾地区政府应对灾难的问题，任何国家都会作出积极而肯定的回答。

B．国家发政委建议取消每周休息两天的双休制，改设月末连休四天的小黄金周，但此建议要被采纳尚需有关部门达成共识。

C．针对部分社会成员之间收入悬殊很大的问题，政府部门要及时采取政策措施，保护合法收入，取缔非法收入，调节过高收人。

D．当今世界，自主知识产权所占比重是衡量一个国家科学发展水平的标志，而科学技术能不能进步是国家富强的标志。

重庆西南师大附中2009届高三2月月考数学文科2009年2月本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．共150分，考试时间120分钟．第Ⅰ卷 （选择题 共60分）一、选择题：本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.直线x +1=0的倾斜角是（ ）A ．30°B ．60°C ．120°D ．150°2.若集合A = {1，m 2}，B = {2，4}，则“m = 2”是“A ∩B = {4}”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3.已知向量a b ，是非零向量，且(2)(2)a b a b a b -⊥-⊥，，则a b 与的夹角为（ ） A ．6πB ．3π C ．23π D ．54π 4.定义在R 上的函数()f x 是奇函数又是以2为周期的周期函数，那么(1)(2)(3)(4)(5)(6)(7)f f f f f f f ++++++=（ ）A ．6B ．5C ．7D ．05.设函数()cos sin ()f x x x f x =-，把的图象按向量(0)(0)a m m =>，平移后，图象恰好为函数sin cos y x x =+的图象，则m 的值可以为（ ） A ．4πB ．34πC ．πD ．2π 6.已知双曲线22221(00)x y a b a b-=>>，的左、右焦点为F 1、F 2，设P 是双曲线右支上一点，121F F F P 在上的投影的长度恰为1F P ，且它们的夹角为6π，则双曲线的离心率e 为（ ）A 1B 1C D7.已知a > 0，b > 0，a ，b 的等差中项是12，且1a a α=+，1b bβ=+，则αβ+的最小值是（ ）A ．3B ．4C ．5D ．68.函数2log (2)2xy x x =>-的反函数的定义域为（ ） A ．(0，+∞)B ．RC ． (－∞，0)D ．（0，1）9.设a =cos 2511221log tan 70log sin 25()2b c ︒︒=︒=，，，那么a 、b 、c 的大小顺序是（ ）A ．a < b < cB ．b < c < aC ．a < c < bD ．c < a < b10.已知抛物线y 2＝8x ，O 是坐标原点，F 是焦点，P 是抛物线上的点，使得△POF 是直角三角形，则这样的P 点共有（ ） A ．0个B ．2个C ．4个D ．6个11.双曲线22221x y a b-=的虚轴端点与一个焦点连线的中点在与此焦点对应的准线上，PQ 是双曲线的一条垂直于实轴的弦，O 为坐标原点．则OP OQ 等于（ ）A ．0B ．2aC ．2a - D ．22a12.如图，设P 、Q 为△ABC 内的两点，且2155AP AB AC =+，AQ =23AB +14AC ，则△ABP 的面积与△ABQ 的面积之比为（ ）A ．15B ．45C ．14D ．13第II 卷 （共90分）二、填空题：本大题共4小题，每题4分，共16分． 13.设α是第三象限角，tan α=512，则cos()πα-=__________． 14.已知数列{}n a 是等比数列，其前n 项和n S ，若3S =1，公比q =2，则6S =_______． 15.已知函数()y f x =是定义在R 的奇函数，当x > 0时，()2f x x =-，那么不等式1()2f x <的解集是_________________．16.如果点P 在平面区域101020x x y y -≤⎧⎪+-≥⎨⎪-≤⎩上，点Q 在曲线22(21x y ++=）上，那么||PQ 的最小值为______________．17.解答题：本题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤． (13分) 已知向量(sin cos )m A A →=，，1)n →=-，1m n →→=，且A 为锐角．(Ⅰ) 求角A 的大小；(Ⅱ) 求函数()cos24cos sin ()f x x A x x =+∈R 的值域．18.(13分) 已知等差数列{}n a 的公差d 大于0，且25a a ，是方程212270x x -+=的两根，数列{}n b 的前n 项和为11(*)2n n n T T b n N =-∈，且．(1) 求数列{}n a 、{}n b 的通项公式； (2) 记{}n n n n c a b c =，求数列的前n 项和S n ．19.(12分) 已知函数()(0)f x a >的图象与直线20x y +-=相切．(1) 求a 的值；(2) 求函数y x =20.(12分) 已知函数21()log 1mx f x x-=-是奇函数． (1) 求m 的值；(2) 解关于x 的不等式1()(1)f x b b R b b ->∈<-，是常数，．21.(12分) 平面直角坐标系中，O 为坐标原点，给定两点A （1，0）、B （0，– 2），点C 满足： O C O A O B αβα=+，其中、21R βαβ∈-=，且 (1) 设点C 的轨迹与椭圆22221(0)x y a b a b +=>>交于两点M 、N ，且以MN 为直径的圆过原点，求证：2211a b+为定值；(2) 在 (1) ，求椭圆实轴长的取值范围．22.(12分) 已知数列{a n }为等差数列．若a 1 = 3，公差d = 1，且212348m a a a a ++++≤，求m 的最大值；对于给定的正整数m ，若221112211m m m m a a S a a a +++++==++，求的最大值．数学试题参考答案（文）一、选择题：本大题共12小题，每题5分，共60分． （2009年2月） 1．D 2．A 3．B 4．D 5．D 6．B 7．C 8．A 9．C 10．B 11．B12．B二、填空题：本大题共4小题，每题4分，共16分． 11．1213 12．9 13． 53|022x x x ⎧⎫≤<<-⎨⎬⎩⎭或 141- 三、解答题：本题共6小题，共74分．17．解：(Ⅰ)由题意得13sin cos 1,2sin()1sin()662m n A A A A ππ=-=∴-=∴-=，由A 为锐角得66A ππ-=，3A π=(Ⅱ)由(Ⅰ)知1cos 2A =,所以2()cos22sin 12sin 2sin f x x x x x =+=-+2132(sin )22x =--+因为x R ∈,所以[]sin 11x ∈-，,因此，当1sin 2x =时,()f x 有最大值32,当sin 1x =-时,()f x 有最小值 – 3，所以所求函数()f x 的值域是332⎡⎤-⎢⎥⎣⎦，18．解：(1) 由25251227.a a a a +==， 且d > 0，所以2539a a ==，，从而521213a a d a -===，，21(*)n a n n N ∴=-∈ 在已知11211.23n n T b n b =-==中，令，得当1212n n n T b ≥=-时，，1111111222n n n n n T b b b b ---=-=-，两式相减得，，11(2)3n n b n b -∴=≥ 1212()(*)333n n n b n N -∴==∈ (2) nn n n n c 32432)12(-=⋅-= 23135212()3333n n n S -∴=++++23n S =231132321()3333n n n n +--++++223n S ∴=231111121[2()]33333n n n +-++++-11112(1)121932[]13313n n n -+--=+--11111214442()333333n n n n n ++-+=+--=- 2223n n n S +∴=-19．解：(1)由220)0y a x y a y ⎧=->⎨≥⎩得即220x y ay ⎧+=⎨≥⎩∴ ()y f x =的图象为圆22x y a +=的上半部分 ∵ 它与直线20x y +-=相切 ∴∴ a = 2(2)令()22x ππαα-≤≤，则2sin()4y πααα==+∵ 22ππα-≤≤∴ 3444πππα-≤+≤∴sin()14πα≤+≤ ∴值域为[2]20．解：(1)()()0f x f x -+=由恒成立22222222211111()log log 0log ()log 11111111()111()log (1)1mx mx mx mx mx x x x x x mx x m m f x m -------⇒+=⇒⋅=⇒=+-+--⇒-=-⇒=±==-∴=-当时，无意义，(2) 可求得，121()21x x f x -+=-11212(1)2(1)()021(1)(1)2(0),0(1)[(1)(1)]0 ,111,. 1111210,0,101111 221, 1x x x x x b b f x b b t b t t t b t b t b t t b b b b b t t b b b b b ---+>⇔<---+=><⇔---+<-+==-∴<-++--<>-=-=>---+∴<>- 令则① 两根当时，或21log 01b x x b +∴<>-或21．解：(1) 222211x y x y ab +=⎧⎪⎨+=⎪⎩由 得：(a 2 + b 2)x 2 – 2a 2x + a 2 – a 2b 2 = 0设M （x 1，y 1），N （x 2，y 2），则x 1 + x 2 =2222a a b +， x 1x 2 =22222a a b a b -+因为以MN 为直径的圆过原点为，所以OM ON =0，即x 1x 2 + y 1y 2 = 0∴ x 1x 2 + (1 – x 1)(1 – x 2) = 1 – (x 1+ x 2) + 2x 1x 2 = 1 –2222a a b ++222222a a b a b -+= 0即a 2 + b 2 – 2a 2b 2 = 0，∴22112a b +=为定值．(3) 2222222223311,2,421a b a e e b a a b a -≤∴=≤+=∴=-22131214002214a a a a ∴-≤-≤∴<≤<≤-，即，∴椭圆实轴长的取值范围是（]．22．解：(1) 由212348m a a a a ++++≤，可得21112348m a a a a a a -+++++≤，又a 1 = 3，d = 1，即(1)63482m m m -++≤ 解得127m -≤≤，又1m ≥， ∴ 17m ≤≤，即m 的最大值为7 (2) 1211221(1)()2m m m m m m a a S a a a +++++++=+++=设121121*********m m m m m m m a a A A a a a a a a a a a ++++++++==++-=+-=-，则，则113m A a a ++=由22221111()1102903A a a a Aa A ++=++-=，得，22440(9)0A A ∆=--≥解得A ≤∴ (1)2m A S +=≤即S。

西南师大附中高2009级第八次月考数学试题（理）本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分．共150分，考试时间120分钟． 参考公式：如果事件A 、B 互斥，那么()()()P A B P A P B +=+ 如果事件A 、B 相互独立，那么()()()P A B P A P B =如果事件A 在一次实验中发生的概率是P ，那么它在n 次独立重复实验中恰好发生k 次的概率()(1)k k n k n n P k C P P -=-球的表面积公式24S R π=，其中R 表示球的半径球的体积公式343V R π=，其中R 表示球的半径 注意事项：1．答题前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上． 2．选择题每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题上．3．填空题的答案和解答题的解答过程直接写在答题卡Ⅱ上． 4．考试结束，监考人将本试题和答题卡一并收回．第I 卷（选择题，共50分）一、选择题：（本大题10个小题，每小题5分，共50分）各题答案必须答在答题卡上． 1． 若全集I = {1，2，3，4，5}，B = {3，4} 满足条件：{34}AB =，的集合A 有n 个，则n 的值为（ ） A ．6B ．7C ．8D ．92．复数式12i ⎛⎫÷ ⎪ ⎪⎝⎭的值为（ ）A ．12i + B ．12i +C ．12i D ．123． 要从其中有50个红球的1000个形状相同的球中，采用按颜色分层抽样的方法抽取100个进行分析，则应抽取红球的个数为（ ） A ．5个B ．10个C ．20个D ．45个4． 函数()f x 1x ≤-）的反函数1()fx -的解析式为（ ）A ．1()f x -=0x ≥）B ．1()f x -=（0x ≤）C ．1()fx -0x ≤）D ．1()fx -=（0x ≥）5． 数列{}n x 中，若11x =，1111n n x x +=-+，则2009x 的值为（ ）A ．12-B ．1C ．12D ．– 16． 已知28(x 的展开式的第7项等于56，则2111lim ()nn x xx →∞+++等于（ ） A ．0B ．1C ．2D ．– 17． 点P 为双曲线2212524x y -=右支上的动点，F 1为双曲线的左焦点，M 为线段PF 1的中点，O 为坐标原点，则 | OM | 的取值范围为（ ） A ．[0,)+∞B ．[2,)+∞C ．1[,)2+∞D ．[1,)+∞8． △ABC 内角A 、B 、C 的对边分别a 、b 、c ，其中a 、b 、c 成等比数列，A 、B 、C 成等差数列．若△ABC 外接圆半径R 为1，则a 的值为（ ）A ．B C ．32 D ．39． ACBA1B1C1三棱柱ABC－A1B1C1中，AA1 = 3，∠A1AB =∠A1AC = 45°，AB = BC = CA，则此三棱柱的高为（）A BC D10．正方体ABCD－A1B1C1D1的上底面A1B1C1D1所在平面内一动点P，它到D点的距离为它到直线B1C1的距离的2倍，则P点的轨迹是（）A．圆B．椭圆C．双曲线D．抛物线第II 卷（非选择题，共100分）二、填空题：（本大题5个小题，每小题5分，共25分）各题答案必须填写在答题卡II 上（只填结果，不要过程） 11． 不等式12x x->的解集为__________________．12． 在3次独立实验中，事件A 出现的概率相同，若事件A 至少发生1次的概率为6364，则事件A在1次实验中发生的概率为___________________．13． 已知实数x 、y 满足不等式组3510830326x y x y y x +≤⎧⎪++≥⎨⎪-≤⎩，则z x y=+的最大值为_________________．14． 若OA a =，OB b =，且1a b a b =-=，则△OAB 的面积的最大值等于__________．15． 将编号为1，2，3，4，5的5封信，分别放入编有1，2，3，4，5号的信箱，每个信箱只能放一封信，要求k 号信不能放在k 号信箱中（k = 1，2，3，4，5），则不同的放法种数为___________________．三、解答题：（本大题6个小题，共75分）各题解答必须答在答题卡II 上（必须写出必要的文字说明、演算步骤或推理过程）．16． （13分）已知函数()2sin()184f x x ππ=++(1) 在所给的坐标纸上作出函数(),[2,14]y f xx =∈-的图象（不要求写出作图过程）．(2)令)()()(x f x f x g -+=，x R ∈.求函数()g x 的最小值以及取得最小值时所对应的x 的集合．17． (13分) 某射手A 第n 次射击时击中靶心的概率为1()1P n n =+（n = 1，2，…）．(1) 求A 射击5次，第5次才击中靶心的概率P ； (2) 若A 共射击3次，求A 击中次数ξ的分布列和期望．18． (13分) 已知函数21()ln 2f x x a x =-，()y f x =的图象在点P （2，(2)f ）处的切线方程为l ：y x b =+．(1) 求出函数()y f x =的表达式和切线l 方程；(2) 当1[,]x e e ∈时（其中e = 2.71828 …），不等式()f x k <恒成立，求实数k 的取值范围．19．AEB S F D(12分) 如图已知：三棱锥S －ABD 中，E 、F 分别为AB 、SD 的中点，若∠SAB =∠SAD =∠BAD = 60°，AB = 2，SA = AD = 1．(1) 求：异面直线SA 与EF 的所成角的大小； (2) 求A 到平面SDB 的距离．20． (12分) 如图，设F 是椭圆2222:1x y C a b +=（a > b > 0）的左焦点，直线l 为其左准线，直线l与x 轴交于点P ，线段MN 为椭圆的长轴，已知||8MN =，且||2||PM MF =．(1) A B F N O M P l x y求椭圆C 的标准方程；(2) 若过点P 的直线与椭圆相交于不同两点A 、B ．求证：∠AFM =∠BFN ； (3) 求△ABF 面积的最大值．21． (12分) 已知函数()1x xb ax ax e f x e ++=+（x R ∈），且1(0)2f =， (1) 若()f x 是减函数，求实数a 的最大值；(2) 若()y f x =在x = 1处的切线与y 轴交于点B ，且A （1，(1)f ），求2()||d a AB =（a > 0）的最小值； (3) 设(1)(2)()n M f f f n =+++，当a = 2时，求证：256n M n n <++（n N +∈）．西南师大附中高2009级第八次月考数学试题参考答案（理）一、选择题1．C 2．A 3．A 4．D 5．B 6．B 7．D 8．B 9．C 10．C 二、填空题11．1{|}3x x < 12．3413．414．15．44三、解答题 16． (1) 列表：描点作图，得图象如下：(2)1)48sin(21)48sin(2)()()(++-+++=-+=ππππx x x f x f x g28cos222)48sin(2)48sin(2+=+--+=x x x πππππ∴当πππk x 28+=，即},168{Z k k x x x ∈+=∈时函数)(x g 取得最小值222- 17．解：(1)11141123411(1)(1)(1)(1)234562345630P =---⨯-⨯=⨯⨯⨯⨯=(2) 设击中ξ次的概率为P 1（ξ），则ξ= 0，1，2，3故11111231(0)(1)(1)(1)2342344P =-⨯--=⨯⨯=⊗ 111111111111(1)(1)(1)(1)(1)(1)(1)23423423424P =⨯--+-⨯⨯-+--⨯= 11111111111111(2)(1)(1)(1)234234234812244P =⨯-+-⨯+-⨯⨯=++=11111(3)23424P =⨯⨯=期望：111111131301234244242422412E ξ=⨯+⨯+⨯+⨯=++=18．解：(1) ∵'()a f x x x =-∴'(2)212a f =-=，a = 2，21()2ln 2f x x x =-∵ 点P （2，(2)f ）满足21()2ln 2f x x x =-∴ (2)22ln 2f =-∵ 点P （2，(2)f ）在直线y = x + b 上 ∴ 2ln 2b =-，直线l ：2ln 2y x =-(2) 由(1)知21()2ln 2f x x x=-，2'()f x x x =-=当'()0f x =，∴ x =随x 的变化，()f x 、'()f x 的变化如下表：由表可知当[,]x e e ∈时，函数()y f x =的最大值为222e + ∴2122k e >+19．解：(1) 取AD 的中点M ，连ME 、MF ，由已知//MF SA ，1122MF SA ==AE B SF D M∵ AD = 1，AB = 2，∠DAB = 60°，∠ADB = 90°∴ BD =ME 且SA 与EF 的所成角为MF 与EF 的所成角连结SE 、ED ，则112ED AB == ∵ ∠SAB = 60°，则∠ASB = 90°∴ 112SE AB == 又∵∠SAD = 60° ∴ SD = AD = SA = 1A EB S F D M NO在等边△SDE 中，∴EF =∴133cos MFE +-∠===即SA 与EF所成角大小为arc(2) 作SO ⊥面ABD 于O ，连AO ，由∠SAB = ∠SAD =∠BAD = 60°∴ AO 是∠BAD 的平分线，∠OAB = 30°则cos cos cos SAO OAB SAB ∠∠=∠，得1cos SAO ∠==∴sin SO SA SAO =∠==121sin 602ABD S ∆=⨯⨯⨯︒=由SD = 1，在Rt △ASB中可得SB =，又在Rt △ADB中BD可得SDB S ∆=设A 到面SBD 的距离为h ，则1133SDB A SDB S ABDABDh S V V SO S--∆⨯===即x ==，即A 到平面SBD 的距离为解法二：(1) 设AB a =，AD b =，AS c =，由已知||2a =，||||1b c ==，2cos601a b =︒=，1a c =，12b c =111()222EF ED DF EA AD DS AB AD DA AS =+=++=-+++ 11()()22AS AD AB c b a =+-=+-1111[()](11)2224EF AS c c b a =⨯+-=+-=22113||()(114122)424EF c b a =+-=+++--=∴3||EF =，||1AS =∴14cos ,EF AS<>===故异面直线EF 与AS 所成角为(2) 设A 到面SBD 的射影为H ，由于H 、S 、D 、B 四点共面∴ AH x AB y AD z AS xa yb zc =++=++，且1x y z ++= 由0()()06AH BD xa yb zc b a z x =⇒++-=⇒=- 又由0()()06AHSD xa yb zc c a y x =⇒++-=⇒=-∴111x =-，611y z ==，即1(66)11AH b c a =++1||(66)11AH b c a =++=，即A 到面SBD 20．解：(1) ∵ ||8MN =，故a = 4又||2||PM MF =得22()a a a c c -=-，即2123102e e e -+=⇒=或e = 1（舍去）∴ c = 2，22212b a c =-=∴ 椭圆的标准方程为2211612x y +=(2) ①当AB 的斜率为0时，显然0AFM BFN ∠=∠=满足题意②当AB 的斜率不为0时，设A （x 1，y 1），B （x 2，y 2）， AB 方程为x = my – 8，代入椭圆方程整理得22(34)481440m y my +-+=由△> 0，则222(48)4144(34)04m m m -⨯+>⇒>又1224834m y y m +=+，12214434y y m =+ ∴121212122266AF BF y y y y k k x x my my +=+=+++--12121226()(6)(6)my y y y my my -+==--∴0AF BF k k +=，从而AFM BFN ∠=∠ 综上可知：恒有AFM BFN ∠=∠(3)211||||2ABF PBF PAFS S S PF y y ∆∆∆=-=-=72==≤=当且仅当2283m =（此时适合△> 0的条件）取得等号∴ △ABF面积的最大值是21．解：(1) 由1(0)2f =，即1122b b =⇒=，则1()1x f x ax e =++，2'()(1)x x e f x a e =-+∵ ()f x 递减 ∴ '()0f x <恒成立，即2(1)xx e a e <+恒成立设2()(1)xx e g x e =+，令xt e =，则(0,)t ∈+∞21()(1)2t g x t t t ==+++其值域1(0,]4 ∴ 0a ≤，即a 的最大值为0(2) 由(1)1(1)1f a e =++，即A （1，11a e ++），2'(1)(1)ef a e=-+∴ ()y f x =在x = 1处的切线方程为21()()(1)1(1)e y a a x e e -+=--++当x = 0时，212(1)ey e +=+，即B （0，212(1)e e ++）故222()||1()(1)ed a AB ae ==+-+∵ a > 0，2(1)ee >+故2(1)e a e =+时，min 1d = (3) 由a = 2，∴2111()222211 1.62()5x x x f x x x x xe =+<+≤+=+++⨯∴21555(1)(2)()[()()]2(12)2888n n M f f f n n =+++<+++++++255(1())155588[](1)[1()](1)5268618n n n n n n n n -=++=-++<++-。

西南师大附中高2009级第七次月考数学试题（文）2009年4月本试卷分第I 卷（选择题）和第n 卷（非选择题）两部分.共 分钟.、选择题：本大题共10小题，每题5分，共50分•在每小题给出的四个选项中，只有 一项是符合题目要求的.1.甲校有3600名学生，乙校有5400名学生，丙校有1800名学生，为统计三校学生某方面的情况，计划采用分层抽样法，抽取一个容量为90的样本，应在这三校分别抽取学A . {x|x ：：:1}B . {x|0 ：：x ：：:2}C . {x|0 ：：x ：：:1}D .^2x , x [0, 1]14.已知函数f(x)二x ，则f (x)的最大值是( )2 , x€(1, 3]3A . 8B . 6C . 3D .-25.函数y =cos(4x •—)的图象的两条相邻对称轴间的距离为()3JinJiA .B . —C .D . ■:8426. 设等比数列｛a n ｝中，前n 项和为S ，已知S 3 =8, S 6 = 7,则a 7+ a 8 + a 9等于（ ）A . 30人，30人， 30人B . 30人，45人， 15人 C.20人，30人， 10人 D.30人，50人， 10人 2. “x > 0, y > 0” 是 2 2xy 2的( )2的（ xyA. 充分不必要条件B . 必要不充分条件C.充要条件D.既不充分也不必要条件 生（ ）3. 已知 M 二｛x|x ：：:1｝,N ={x |log 2x ：：：1}，则 M D N =()150分，考试时间 1207. 平面上的向量 B .C .PB 满足PA PB = 4,且57 8II PA L PB =0,D .55 8若向量 PA , PC则|PC|的最大值为（）9.反复抛掷一个骰子，依次记录下每一次抛掷落地时向上的点数，当记有三个不同点数 时即停止抛掷，若抛掷五次恰好停止，则记有这五次点数的所有不同记录结果的种数 有（ ） C . 600 种 D . 1680 种F 1、F 2是该椭圆的两个焦点，若△ PF 1F 2的内切圆）9C .D . 04二、填空题：本大题共5小题，每题5分，共25分.211. __________________________________________________________________________ 已知双曲线x 2 - — =1的一条渐近线与直线 x-2y ，3 = 0垂直，则a = ________________________ .a 12. 在（x —a ）10的展开式中，x 7的系数是15,则实数a = __________________ .x _0 I13.若A 为不等式组 y _0表示的平面区域，则当 a 从-2连续变化到1时，动直线y —x 兰2x+y=a 扫过 A 中的那部分区域的面积为 ___________________ .14. 已知三棱锥 S — ABC 的各顶点都在一个半径为r 的球面上，球心 0在AB 上，SO 丄底面ABC, AC = J2r ，则三棱锥的体积与球的体积之比是 _____________________ . 15. 以下四个命题：① 厶ABC 中，A > B 的充要条件是si nA ・s in B ; ② 等比数列｛a n ｝中，a 1 = 1, a 5 = 16,则a 3 = 4 ；③ 把函数y =sin （2 -2x ）的图像向右平移2个单位后得到的图像对应的解析式为y =si n （4 —2x ）其中正确的命题的序号是 _________________ .B .C . 4D .-2 28已知方程组 X y a有两组不同的解，则实数22x 亠y 亠6x-8y-11=0a 的取值范围是（A . (1, 121) D . (0, 121)A . 360 种B . 840 种 2 210.已知P 是椭圆— - 1上的一点,4 3 1半径为一，则PF 丄PF 2的值为（2B .三、解答题：本题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤.16. (本小题满分13分)已知A、B、C 是厶ABC 的三个内角，向量m =(_1, 3) , n =(cosA, si nA)，且m • n = 1.(1) 求角A;(2) 若一\ sin 2B23，求tanC 的值.cos B -sin B17. (本小题满分13分)甲、乙两支篮球队进行比赛，已知每一场甲队获胜的概率为0.6，乙队获胜的概率为0.4, 每场比赛均要分出胜负，比赛时采用三场两胜制，即先取得两场胜利的球队胜出.(1) 求甲队以二比一获胜的概率；(2) 求乙队获胜的概率.18. (本小题满分13分)设函数f(x) =ax3 bx c是定义在R上的奇函数，且函数f(x)的图像在x = 1处的切线方程为y =3x • 2 .(1) 求a、b、c的值；k(2) 若对任意(0, 1］都有f(x)^—成立，求实数k的取值范围.x19. (本小题满分12分)TT 如图，在四棱锥P—ABCD中，底面ABCD是直角梯形，ZDAB /ABC二一，且220. (本小题满分12分)设正数数列｛a n｝的前n项和为S n,且对任意的N*, S是a2和a n的等差中项.(1) 求数列｛a n｝的通项公式；(2) 在集合M =｛m|m =2k, k z,且1000 _k :: 1500｝中，是否存在正整数m,使得不2等式S _1005 ,an 对一切满足n > m 的正整数n 都成立？若存在，则这样的正整2数m 共有多少个？并求出满足条件的最小正整数 m 的值；若不存在，请说明理由.21. (本小题满分12分)设A 、B 是椭圆3x 2 • y 2上的两点，点N(1 , 3)是线段AB 的中点，线段 AB 的垂直平分线与椭圆相交于 C 、D 两点.(1) 确定，的取值范围，并求直线 AB 的方程；(2) 求以线段CD 的中点M 为圆心且与直线 AB 相切的圆的方程.西南师大附中高2009级第七次月考数学试题参考答案(文)2009年4月兀 1二 sin(A — —)二一6 2二 二 5 二••• A (，-)6 6 6A - ■ 6 6A 二一3 2 2sin B 2sinBcosB cos B--------------------------------------- =-3 (cosB -sin B)(cos B sin B)sin B cosB 3cosB -sin B tan B 1 1 -ta nAtanB =2、选择题： 本大题共 10小题，每题5分，共50 分.C 4. C6. A7.9. B 10. B二、填空题： 本大题共 5小题，每题 5分，共 25 分. 11. 4 12. 13.-414.-4 二三、解答题： 15.①本题共6小题，共75分.16•解:(1)m U n - cos A -tan A tan B 3 2 8 5 3tanC = -tan(A B):1 -ta nA［ta nB 1-^3 1117•解：(1)甲队以二比一获胜，即前两场中甲胜1场，第三场甲获胜，其概率为1R =C2 X0.6X0.4X0.6=0.288.(2)乙队以2 : 0获胜的概率为P2 =0.4 0.4 =0.16 ；乙队以2 ：1获胜的概率为p2丄C；0.4 0.6 0.4 =0.192.•••乙队获胜的概率为P2=Pk+ P ”2=0.16+0.192=0.352.318.解：(1) ■/函数f(x)二ax bx c是定义在R上的奇函数，••• f(」)-_f(x)3 3a( _x) b( _x) c _ -(ax bx c) •- c = 0 •又f (x)在x =1处的切线方程为y =3x • 2 ,由 f '(x) =3ax2 bf'(1±,且f ⑴=5 , • 3a b=3 得a —［a+b=5 'p=63(2) f(x) - -x 亠6x依题意_x3・6x乞对任意x・(0,1］恒成立，x4 2 2 2二-x 6x _k对任意x = (0,1］恒成立，即k_-(x -3) 9对任意x=(0,1］恒成…k _5 •19•解法一：(1)证明：取AB中点为O，连结PO、OC ,•••△ PAB是等边三角形，• PO — AB又•••侧面PAB _底面ABCD ,•PO _ 底面ABCD ,•OC为PC在底面ABCD上的射影，又T AB =BC =2AD =2 ,ZABC /DAB ,2•DAB = OBC , • BCO = DBA,•BD — OC , • BD — PC .(2)取PC中点E，连结BE、DE ,2•/ PB 二BC . • BE — PC .又••• BD _ PC , BE BD 二B ,•PC _ 平面BDE , • PC _ DE ,•BED是二面角B - PC - D的平面角.••• AB 二BC =2AD =2 , . ABC 二,2• BE =PE J P C =$2,PD =BD =匸5 •220.解:2x2+ y2= 0K 一y2+ V3z2= 0令x2=1, y2= -2，则Z2 - . 3 ,•①二(1,一2,- .. 3)_ n「n? _ .3 1 0 (-2) 1 (- •. 3)n j|“2171 • n1,匕二?，2(1)由题意得，2S^ ~ a n a n当n = 1 时，2a1 = a-|2■ a1•- DC =(2,1,0),DP =(1,-1,3) , •• cos n 1,n2•二面角2 2.2B - PC - D的大小为，解得a1a n42 2①式减去②式得，2a n二a n -a nj2 2当n 一2时，有2S n』=a；/=1 ,于是，a n - a n 4 _ a n a n」,(a n a n 4)(a n - a n」) 因为a n ■ an j - 0，所以a n -a n 4^1 , 所以数列£n ［是首项为1，公差为1的等差数列，所以，a n匚的通项公式为a n二n ( n • N * ).⑵设存在满足条件的正整数m，则四-1005=a nn-1005，n 2010 ,2 2又M 二{ 2000, 2002 ,…，2008, 2010, 2012,…，2998}, 所以m=2010, 2012，…，2998均满足条件，••• DE = . 3 ,••• BE2 DE2二BD2 BED 二二2•二面角B_PC _D的大小为二2证明：⑴取AB中点为O, CD中点为M，连结OM ,•••△ PAB是等边三角形，• PO丄AB ,又•••侧面PAB _底面ABCD，• PO _底面ABCD ,•••以O为坐标原点，建立空间直角坐标系如图，•/ AB =BC -2AD =2 , △ PAB 是等边三角形，•OP = , 3 ,•O(0,0,0), B(1,0,0),C(1,2,0), D( —1,1,0), P(0,0, .. 3).•BD =(-2,1,0),PC 二(1,2, - ...3).•/ BD PC = -2 2 = 0 • BD _ PC .⑵设平面PBC的法向量为n 1 =(洛，力，乙)••• PB =(1,0,-. 3), BC = (0,2,0)令z1=1，则x1 -、3, y1= 0 ,• m = ( 一3,0,1)设平面PCD的法向量为n2= (x2, y2, z2),解法X1 —J3z1 =02y1 =02它们组成首项为2010，公差为2的等差数列.……(8分) 设共有k 个满足条件的正整数，则2010 - 2(k _1) =2998，解得k = 495 . ( 10分)所以，M 中满足条件的正整数 m 存在，共有495个，m 的最小值为2010 .分)21 . (I)法1 :依题意，显然AB 的斜率存在，可设直线 AB 的方程为y =k(x -1)3,代入 3x 2 y 2 二，，整理得 (k 2 3)x 2 _2k(k _3)x (k_3)2 - • =0 . ① 设A (X 1, yJ,B(X 2,y 2),则X 1,X 2是方程①的两个不同的根, ••• & =4[，(k 2 3) -3(k -3)2] 0 , ② 且x1 +x 2=2k(2k 一3)，由N(1,3)是线段AB 的中点，得 k 32=1,二 k(k —3) =k 3 .2解得k = -1，代入② 得，扎＞12,即人的取值范围是(12, +8).于是，直线 AB 的方程为y _3二_(x_1)，即x • y _4=0 法 2：设 A(X 1,yJ ,BXy)，则有丁3x 1 - y f 二22：(人—X 2)(X 1 X 2)卜 1 一丫2)卜 1 丫2)=0・J3X 2 y 2依题意，论=x 2 , • kAB =3(X 1 X 2)T N(1,3)是 AB 的中点，二 X「X2=2 , y 1 y^6，从而 k AB=-1. 又由N(1,3)在椭圆内，•■ 3 12 32 =12 ,• ■的取值范围是(12,；).直线AB 的方程为y-3--(x-1)，即x 亠y-4=0 .(2) T CD 垂直平分AB ，•直线CD 的方程为y-3 = x-1，即x-y ，2 = 0, 代入椭圆方程，整理得 4x 2 • 4x • 4 - ■ = 0 .③又设C(X 3, y 3), D(X 4, y 4) , CD 的中点为M (x °, y °)，则X 3, X 4是方程③的两根, 113 1 3二 X 3 x 4 - -1，且X 0(X 3 X 4) , y 0 = X0 2 ，即M (-一，).2 22 2 2_! +2 _42 22(X 丄)2 (y 一3)2 .2 2 2(12X 1 X 2 y 1 y 23、2= ---------- ?2M (3)到直线AB 的距离d 二 ______________2‘2 .12 1故所求的以线段 CD 的中点M 为圆心且与直线 AB 相切的圆的方程为:。