等腰三角形练习题

等腰三角形的判定练习题等腰三角形是指具有两边长度相等的三角形。

判定一个三角形是否是等腰三角形有多种方法，下面将介绍几个常用的练习题，帮助读者加深对等腰三角形的判定方法的理解。

练习题1：判定三角形的三边是否相等判定一个三角形是否是等腰三角形的最基本方法就是判断三边是否相等。

请读者根据给定的三条边，判断哪些是等腰三角形。

请注意，给定的三条边是任意长度的实数。

练习题2：判定三角形的两个角是否相等判定一个三角形是否是等腰三角形的另一种方法是判断两个角是否相等。

在等腰三角形中，两个底边的对角是相等的。

给定一个三角形的三个角度，请读者判断哪些是等腰三角形。

请注意，给定的角度是任意度数的实数。

练习题3：结合两种判定方法练习题1和练习题2是等腰三角形判定的两种基本方法，但单独使用一个方法可能不够准确。

在实际应用中，结合两种方法可以提高判定的准确性。

给定一个三角形的三边长度和三个角度，请读者结合两种方法并判断哪些是等腰三角形。

练习题4：拓展思考亲自画出不同形状的等腰三角形，并对这些三角形进行判定。

观察不同等腰三角形的性质，思考如何通过形状或者角度的特点更准确地判定一个三角形是否是等腰三角形。

补充练习题：1. 给定一个三角形的边长分别为a、b、c，判断是否为等腰三角形。

2. 给定一个三角形的内角度数分别为α、β、γ，判断是否为等腰三角形。

3. 给定一个三角形的两条底边分别为a、b，判断是否为等腰三角形。

4. 通过观察等腰三角形的形状特点，提供一种更准确的判定方法。

答案及解析：1. 三角形abc是等腰三角形的条件是a=b或者b=c或者a=c。

只要满足这三个条件中的任意一个，那么该三角形就是等腰三角形。

2. 三角形的内角都是180度。

给定的三角形的内角度数为α、β、γ，那么如果α=β或者β=γ或者α=γ，那么该三角形就是等腰三角形。

3. 在等腰三角形中，两条底边对应的顶角相等。

给定的三角形的两条底边为a、b，那么如果a与b对应的顶角相等，那么该三角形就是等腰三角形。

等腰三角形与直角三角形练习题一、等腰三角形练习题（一）基础练习1、已知等腰三角形的一个内角为 70°，则它的另外两个内角的度数分别是（）A 55°，55°B 70°，40°C 55°，55°或 70°，40°D 以上都不对解析：当 70°的角为顶角时，底角的度数为：（180° 70°）÷ 2 ＝55°；当 70°的角为底角时，另一个底角也是 70°，顶角的度数为 180°70°× 2 ＝ 40°。

所以答案选择 C。

2、等腰三角形的两边长分别为 3 和 6，则这个等腰三角形的周长为（）A 12B 15C 12 或 15D 18解析：当腰长为 3 时，3 ＋ 3 ＝ 6，不能构成三角形；当腰长为 6 时，周长为 6 ＋ 6 ＋ 3 ＝ 15。

所以答案选择 B。

（二）提高练习1、如图，在△ABC 中，AB ＝ AC，AD 是∠BAC 的平分线，点 E 在 AD 上。

求证：△EBC 是等腰三角形。

证明：因为 AB ＝ AC，AD 是∠BAC 的平分线，所以 AD⊥BC，BD ＝ CD。

又因为点 E 在 AD 上，所以 EB ＝ EC，即△EBC 是等腰三角形。

2、已知等腰三角形一腰上的中线将其周长分成 9 和 15 两部分，求这个等腰三角形的腰长和底边长。

设腰长为 2x，底边长为 y，则有两种情况：情况一：＼（＼begin{cases}2x ＋ x ＝ 9 ＼＼ x ＋ y ＝ 15\end{cases}＼），解得\（＼begin{cases}x ＝ 3 ＼＼ y ＝ 12\end{cases}＼），此时腰长为 6，底边长为 12，因为 6 ＋ 6 ＝ 12，不符合三角形三边关系，舍去。

情况二：＼（＼begin{cases}2x ＋ x ＝ 15 ＼＼ x ＋ y ＝ 9\end{cases}＼），解得\（＼begin{cases}x ＝ 5 ＼＼ y ＝ 4\end{cases}＼），此时腰长为 10，底边长为 4，符合三角形三边关系。

等腰三角形与直角三角形练习题一、等腰三角形练习题（一）基础巩固1、已知等腰三角形的一个内角为 80°，则它的另外两个内角分别是多少度？解：当 80°的角为顶角时，底角的度数为：（180° 80°）÷ 2 ＝ 50°，所以另外两个内角分别是 50°，50°。

当 80°的角为底角时，顶角的度数为：180° 80°× 2 ＝ 20°，所以另外两个内角分别是 80°，20°。

2、等腰三角形的两边长分别为 6 和 8，则其周长是多少？解：当腰长为 6 时，三边长分别为 6，6，8，因为 6 ＋ 6＞8，所以能组成三角形，此时周长为 6 ＋ 6 ＋ 8 ＝ 20。

当腰长为 8 时，三边长分别为 8，8，6，因为 8 ＋ 6＞8，所以能组成三角形，此时周长为 8 ＋ 8 ＋ 6 ＝ 22。

综上，其周长为 20 或 22。

3、一个等腰三角形的周长为 20，其中一边长为 8，求另外两边的长。

解：当 8 为腰长时，底边长为 20 8× 2 ＝ 4，因为 8 ＋ 4＞8，所以能组成三角形，此时另外两边长分别为 8，4。

当 8 为底边时，腰长为(20 8)÷ 2 ＝ 6，因为 6 ＋ 6＞8，所以能组成三角形，此时另外两边长分别为 6，6。

（二）能力提升1、等腰三角形一腰上的高与另一腰的夹角为 30°，则顶角的度数为多少？解：当等腰三角形为锐角三角形时，腰上的高与另一腰的夹角为30°，则顶角为 60°。

当等腰三角形为钝角三角形时，腰上的高与另一腰的夹角为 30°，则顶角的外角为 60°，所以顶角为 120°。

综上，顶角的度数为 60°或 120°。

2、如图，在△ABC 中，AB ＝ AC，D 是 BC 边上的中点，∠B ＝30°，求∠1 和∠ADC 的度数。

等腰三角形练习题等腰三角形练习题等腰三角形是初中数学中的一个重要概念，也是几何学中常见的一种形状。

它具有特殊的性质和特点，因此在数学教学中，经常会出现与等腰三角形相关的练习题。

下面我将为大家介绍几道关于等腰三角形的练习题，希望能帮助大家更好地理解和掌握这一概念。

练习题一：已知等腰三角形ABC中，AB = AC，角A = 40°，求角B和角C的度数。

解析：由于等腰三角形的定义，我们知道AB = AC，因此角B和角C的两边也相等。

又已知角A = 40°，所以角B和角C的度数相等，设为x。

根据三角形内角和定理，我们可以得到40° + x + x = 180°，化简得2x = 140°，解方程可得x = 70°。

所以角B和角C的度数均为70°。

练习题二：已知等腰三角形ABC中，AB = AC = 8cm，角B = 50°，求三角形的周长和面积。

解析：由于等腰三角形的定义，我们知道AB = AC = 8cm，角B = 50°。

首先，我们可以通过余弦定理求得三角形的底边BC的长度。

根据余弦定理，我们有cosB = (AB^2 + AC^2 - BC^2) / (2AB * AC)，代入已知条件，可以得到cos50° = (8^2 + 8^2 - BC^2) / (2 * 8 * 8)，化简可得BC^2 = 128 - 128 * cos50°，计算可得BC ≈ 9.62cm。

接下来，我们可以求三角形的周长。

由于等腰三角形的两边相等，所以周长等于AB + AC + BC = 8 + 8 + 9.62 ≈ 25.62cm。

最后，我们可以求三角形的面积。

由于等腰三角形的高线可以通过顶角的平分线构造出来，所以我们可以通过高线计算面积。

设高线的长度为h，根据三角形面积公式，我们有面积S = (1/2) * AB * h。

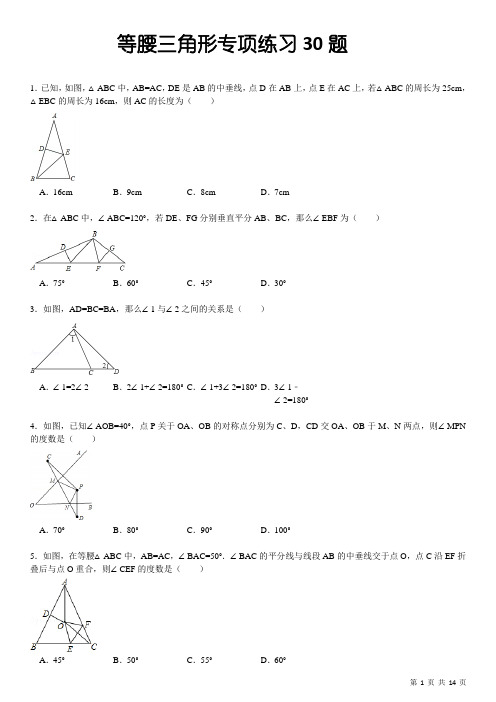
等腰三角形专项练习30题1．已知，如图，△ABC中，AB=AC，DE是AB的中垂线，点D在AB上，点E在AC上，若△ABC的周长为25cm，△EBC的周长为16cm，则AC的长度为（）A．16cm B．9cm C．8cm D．7cm2．在△ABC中，∠ABC=120°，若DE、FG分别垂直平分AB、BC，那么∠EBF为（）A．75°B．60°C．45°D．30°3．如图，AD=BC=BA，那么∠1与∠2之间的关系是（）A．∠1=2∠2 B．2∠1+∠2=180°C．∠1+3∠2=180°D．3∠1﹣∠2=180°4．如图，已知∠AOB=40°，点P关于OA、OB的对称点分别为C、D，CD交OA、OB于M、N两点，则∠MPN的度数是（）A．70°B．80°C．90°D．100°5．如图，在等腰△ABC中，AB=AC，∠BAC=50°．∠BAC的平分线与线段AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是（）A．45°B．50°C．55°D．60°6．如图所示，△ABC为正三角形，P是BC上的一点，PM⊥AB，PN⊥AC，设四边形AMPN，△ABC的周长分别为m、n，则有（）A．B．C．D．7．如图所示，AB=AD，∠ABC=∠ADC=90°，则①AC平分∠BAD；②CA平分∠BCD；③AC垂直平分BD；④BD平分∠ABC，其中正确的结论有（）A．①②B．①②③C．①②③④D．②③8．下列说法正确的是（）A．两个能重合的图形一定关于某条直线对称B．若两个图形关于某直线对称，则它们的对应点一定位于对称轴的两侧C．到角两边距离相等的点在这个角的平分线上D．如果三角形一边的垂直平分线经过它的一个顶点，那么这个三角形一定是等腰三角形9．用一根长为a米的线围成一个等边三角形，测知这个等边三角形的面积为b平方米．现在这个等边三角形内任取一点P，则点P到等边三角形三边距离之和为（）米．A．B．C．D．10．在等腰直角△ABC（AB=AC≠BC）所在的三角形边上有一点P，使得△PAB，△PAC都是等腰三角形，则满足此条件的点有（）A．1个B．3个C．6个D．7个11．如图所示，在△ABC中，AB=AC，腰AB的垂直平分线交另一腰AC于点D，BD+CD=10cm，则AB的长为_________．12．如图，若等腰△ABC的腰长AB=10cm，AB的垂直平分线交另一腰AC于D，△BCD的周长为16cm，则底边BC是_________cm．13．已知实数x，y满足|x﹣4|+（y﹣8）2=0，则以x，y的值为两边长的等腰三角形的周长是_________．14．如图所示，将两个全等的有一个角为30°的直角三角形拼在一起，其中两条较长直角边在同一条直线上，则图中等腰三角形有_________个．15．如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=8，BC=5，则BD的长为_________．16．等腰△ABC的底边上高AD与底角平分线CE交于点P，EF⊥AD，F为垂足，则线段EB与线段EF的数量关系为_________．17．如图，在等腰在△ABC中，AB=27，AB的垂直平分线交AB于点D，交AC于点E，若在△BCE的周长为50，则底边BC的长为_________．18．等腰△ABC中，AB=AC，一腰上的中线BD将这个等腰三角形的周长分成15和6两部分，则这个三角形的腰长为_________．19．如图，已知D为等边三角形纸片ABC的边AB上的点，过点D作DG∥BC交AC于点G，DE⊥BC于点E，过点G作GF⊥BC于点F．把三角形纸片ABC分别沿DG，DE，GF按图示方式折叠，则图中阴影部分是_________三角形．20．如图，△ABC中，D、E分别是AC、AB上的点，BD与CE交于点O．给出下列三个条件：①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD．上述三个条件中，哪两个条件可判定△ABC是等腰三角形（用序号写出一种情形）：_________．21．如图，已知等边△ABC边长为1，D是△ABC外一点且∠BDC=120°，BD=CD，∠MDN=60°．求证：△AMN的周长等于2．22．如图所示，在△ABC中，∠C=90°，BD平分∠ABC交AC于点D，过点D作DE∥BC交AB于点E，过点D作DF⊥AB于点F，说明：BC=DE+EF成立的理由．23．如图，在等腰Rt△ABC中，∠ACB=90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，连接CF．（1）求证：AD⊥CF；（2）连接AF，试判断△ACF的形状，并说明理由．24．已知：如图，P、Q是△ABC边BC上两点，且BP=PQ=QC=AP=AQ，求∠BAC的度数．25．如图，∠1=∠2，AB=AD，∠B=∠D=90°，请判断△AEC的形状，并说明理由．26．如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于H，①求证：△BCE≌△ACD；②求证：CF=CH；③判断△CFH的形状并说明理由．27．如图：△ABC是等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD于Q，PQ=3，PE=1，求AD的长．28．如图，在等腰△ABC中，CH是底边上的高线，点P是线段CH上不与端点重合的任意一点，连接AP交BC于点E，连接BP交AC于点F．（1）证明：∠CAE=∠CBF；（2）证明：AE=BF．29．如图，在△ABC中，已知AB=BC=CA，AE=CD，AD与BE交于点P，BQ⊥AD于点Q，求证：BP=2PQ．30．如图，△ABE和△BCD都是等边三角形，且每个角是60°，那么线段AD与EC有何数量关系？请说明理由．参考答案：1．解：∵DE是AB的垂直平分线，∴AE=BE，∵△ABC的周长为25cm，△EBC的周长为16cm，AC=AB，∴2AC+BC=25cm，BE+CE+BC=AE+EC+BC=AC+BC=16cm，即，解得：AC=9cm，故选B2．解：∵DE、FG分别垂直平分AB、BC，∴AE=BE，BF=CF，∴∠A=∠ABE，∠C=∠CBF，∵∠A+∠C+∠ABC=180°，∠ABC=120°，∴∠A+∠C=60°，∴∠ABE+∠CBF=60°，∴∠EBF=120°﹣60°=60°，故选B3．解：∵AB=BC，∴∠1=∠BCA，∵AB=AD，∴∠B=∠2，∵∠1+∠B+∠ACB=180°，∴2∠1+∠2=180°．故选B4．解：∵P关于OA、OB的对称∴OA垂直平分PC，OB垂直平分PD∴CM=PM，PN=DN∴∠PMN=2∠C，∠PNM=2∠D，∵∠PRM=∠PTN=90°，∴在四边形OTPR中，∴∠CPD+∠O=180°，∴∠CPD=180°﹣40°=140°∴∠C+∠D=40°∴∠MPN=180°﹣40°×2=100°故选D．5．解：如图，延长AO交BC于点M，连接BO，∵等腰△ABC中，AB=AC，∠BAC=50°，∴∠ABC=∠ACB=（180°﹣50°）÷2=65°，∵AO是∠BAC的平分线，∴∠BAO=25°，又∵OD是AB的中垂线，∴∠OBA=∠OAB=25°，∴∠OBM=∠OCM=60°﹣25°=40°，∴∠BOM=∠COM=90°﹣40°=50°，由折叠性可知，∠OCM=∠COE，∴∠MOE=∠COM﹣∠COE=50°﹣40°=10°，∴∠OEM=90°﹣10°=80°，∵由折叠性可知，∠OEF=∠CEF，∴∠CEF=（180°﹣80°）÷2=50°．故选：B6．解：设BM=x，CN=y则BP=2x，PC=2y，PM=x，PN=yAM+AN=2BC﹣（BM+CN）=3（x+y），故==≈0.7887．故选D7．解：在Rt△ABC和Rt△ADC中，AB=AD，AC=AC，所以Rt△ABC≌Rt△ADC（HL）．所以∠ACB=∠ACD，∠BAC=∠DAC，即AC平分∠BAD，CA平分∠BCD．故①②正确；在△ABD中，AB=AD，∠BAO=∠DAO，所以BO=DO，AO⊥BD，即AC垂直平分BD．故③正确；不能推出∠ABO=∠CBO，故④不正确．故选B8．解：A、两个能重合的图形不一定关于某条直线对称，故错误；B、两个图形关于某条直线对称，它们的对应点有可能位于对称轴上，故错误；C、同一平面内，到角的两边距离相等的点在角的平分线上，故错误；D，正确，故选D9．解：等边三角形周长为a，则边长为，设P到等边三角形的三边分别为x、y、z，则等边三角形的面积为b=××（x+y+z）解得x+y+z=，故选C10．解：∵△ABC是等腰直角三角形，（AB=AC≠BC）所在的三角形边上有一点P，使得△PAB，△PAC都是等腰三角形，∴有一个满足条件的点﹣斜边中点，∴符合条件的点有1个．故选A．11．解：∵ED是边AB边上的中垂线，∴AD=BD；又∵BD+CD=10cm，AB=AC，∴BD+CD=AD+DC=AC=AB=10cm，即AB=10cm．故答案是：10cm12．解：∵DE是线段AB的垂直平分线，∴AD=BD，∴BD+CD=AC，∵AB=AC=10cm，BD+CD+BC=AB+BC=16cm，∴BC=16﹣AB=16﹣10=6cm．故答案为：6cm13．解：根据题意得，x﹣4=0，y﹣8=0，解得x=4，y=8，①4是腰长时，三角形的三边分别为4、4、8，∵4+4=8，∴不能组成三角形，②4是底边时，三角形的三边分别为4、8、8，能组成三角形，周长=4+8+8=20，所以，三角形的周长为20．故答案为：2014．解：∵将两个全等的有一个角为30°的直角三角形拼在一起，其中两条较长直角边在同一条直线上．∴EF∥DG，∠E=∠D=60°，∴∠ENM=∠D=60°，∠MGD=∠E=60°，∴EM=NM=EN，DM=GM=DG，∴△MEN，△MDG是等边三角形．∵∠A=∠B=30°，∴MA=MB，∴△ABM是等腰三角形．∴图中等腰三角形有3个15．解：延长BD与AC交于点E，∵∠A=∠ABD，∴BE=AE，∵BD⊥CD，∴BE⊥CD，∵CD平分∠ACB，∴∠BCD=∠ECD，∴∠EBC=∠BEC，∴△BEC为等腰三角形，∴BC=CE，∵BE⊥CD，∴2BD=BE，∵AC=8，BC=5，∴CE=5，∴AE=AC﹣EC=8﹣5=3，∴BE=3，∴BD=1.5．故选A．16．解：延长EF交AC于点Q，∵EF⊥AD，AD⊥BC∴EQ∥BC∴∠QEC=∠ECB∵CE平分∠ACB∴∠ECB=QCE∴∠QEC=∠QCE∴QE=QC∵QE∥BC，且△ABC为等腰三角形∴△AQE为等腰三角形∴AQ=AE，QE=2EF∴BE=CQ=2EF．故答案为：BE=2EF．17．解：∵DE垂直且平分AB，∴BE=AE．由BE+CE=AC=AB=27，∴BC=50﹣27=2318．解：设AB=AC=2X，BC=Y，则AD=CD=X，∵AC上的中线BD将这个三角形的周长分成15和6两部分，∴有两种情况：1、当3X=15，且X+Y=6，解得，X=5，Y=1，∴三边长分别为10，10，1；2、当X+Y=15且3X=6时，解得，X=2，Y=13，此时腰为4，根据三角形三边关系，任意两边之和大于第三边，而4+4=8＜13，故这种情况不存在．∴腰长只能是10．故答案为1019．解：∵三角形ABC为等边三角形，∴∠A=∠B=∠C=60°，∵根据题意知道点B和点C经过折叠后分别落在了点I和点H处，∴∠DIH=∠B=60°，∠GHI=∠C=60°，∴∠HJI=60°，∴∠DIH=∠GHI=∠HJI=60°，∴阴影部分是等边三角形，故答案为：等边．20．答：由①③条件可判定△ABC是等腰三角形．证明：∵∠EBO=∠DCO，∠EOB=∠DOC，（对顶角相等）BE=CD，∴△EBO≌△DCO，∴OB=OC，∴∠OBC=∠OCB，∴∠ABC=∠ACB，∴△ABC是等腰三角形21．解：延长AC到E，使CE=BM，连接DE，（如图）∵BD=DC，∠BDC=120°，∴∠CBD=∠BCD=30°，∵∠ABC=∠ACB=60°，∴∠ABD=∠ACD=∠DCE=90°，∴△BMD≌△CDE，∴∠BDM=∠CDE，DM=DE，又∵∠MDN=60°，∴∠BDM+∠NDC=60°，∴∠EDC+∠NDC=∠NDE=60°=∠NDM，又∵DN=DN，∴△MDN≌△EDN（SAS），∴MN=NE=NC+CE=NC+BM，所以△AMN周长=AM+AN+MN=AM+AN+NC+BM=AB+AC=2．22．解：∵BD平分∠ABC，DF⊥AB，∠C是直角，∴CD=DF，∠DBC=∠DBE，∠DFB=∠C，∴△BCD≌△BFD，∴BC=BF，∵DE∥BC，∴∠DBC=∠EDB，即∠DBC=∠DBE，∴△BDE是等腰三角形，∴BE=DE，∴BF=BC=DE+EF23．（1）证明：在等腰直角三角形ABC中，∵∠ACB=90°，∴∠CBA=∠CAB=45°．又∵DE⊥AB，∴∠DEB=90°．∴∠BDE=45°．又∵BF∥AC，∴∠CBF=90°．∴∠BFD=45°=∠BDE．∴BF=DB．又∵D为BC的中点，∴CD=DB．即BF=CD．在△CBF和△ACD中，，∴△CBF≌△ACD（SAS）．∴∠BCF=∠CAD．又∵∠BCF+∠GCA=90°，∴∠CAD+∠GCA=90°．即AD⊥CF．（2）△ACF是等腰三角形，理由为：连接AF，如图所示，由（1）知：CF=AD，△DBF是等腰直角三角形，且BE是∠DBF的平分线，∴BE垂直平分DF，∴AF=AD，∵CF=AD，∴CF=AF，∴△ACF是等腰三角形．24．解：∵BP=PQ=QC=AP=AQ，∴∠PAQ=∠APQ=∠AQP=60°，∠B=∠BAP，∠C=∠CAQ．又∵∠BAP+∠ABP=∠APQ，∠C+∠CAQ=∠AQP，∴∠BAP=∠CAQ=30°．∴∠BAC=120°．故∠BAC的度数是120°25．解：△AEC是等腰三角形．理由如下：∵∠1=∠2，∴∠1+∠3=∠2+∠3，即∠BAC=∠DAE，又∵AB=AD，∠B=∠D，∴△ABC≌△ADE（ASA），∴AC=AE．即△AEC是等腰三角形26．①证明：∵∠BCA=∠DCE=60°，∴∠BCE=∠ACD，在△BCE和△ACD中，，∴△BCE≌△ACD（SAS）；②∵△BCE≌△ACD，∴∠CBF=∠CAH．∵∠ACB=∠DCE=60°，∴∠ACH=60°．∴∠BCF=∠ACH，在△BCF和△ACH中，，∴△BCF≌△ACH（ASA），∴CF=CH；③∵CF=CH，∠ACH=60°，∴△CFH是等边三角形27．解：∵△ABC为等边三角形，∴AB=CA，∠BAE=∠ACD=60°；又∵AE=CD，在△ABE和△CAD中，∴△ABE≌△CAD；∴BE=AD，∠CAD=∠ABE；∴∠BPQ=∠ABE+∠BAD=∠BAD+∠CAD=∠BAE=60°；∵BQ⊥AD，∴∠AQB=90°，则∠PBQ=90°﹣60°=30°；∵PQ=3，∴在Rt△BPQ中，BP=2PQ=6；又∵PE=1，∴AD=BE=BP+PE=728．（1）证明：在等腰△ABC中，∵CH是底边上的高线，∴∠ACH=∠BCH，在△ACP和△BCP中，，∴△ACP≌△BCP（SAS），∴∠CAE=∠CBF（全等三角形对应角相等）；（2）在△AEC和△BFC中，∴△AEC≌△BFC（ASA），∴AE=BF（全等三角形对应边相等）．29．证明：∵AB=BC=CA，∴△ABC为等边三角形，∴∠BAC=∠C=60°，在△ABE和△CAD中∴△ABE≌△CAD（SAS），∴∠ABE=∠CAD，∵∠BPQ=∠ABE+∠BAP，∴∠BPQ=∠CAD+∠BAP=∠CAB=60°，∵BQ⊥AD∴∠BQP=90°，∴∠PBQ=30°，∴BP=2PQ．30．解：AD=EC．证明如下：∵△ABC和△BCD都是等边三角形，每个角是60°∴AB=EB，DB=BC，∠ABE=∠DBC=60°，∴∠ABE+∠EBC=∠DBC+∠EBC即∠ABD=∠EBC在△ABD和△EBC中∴△ABD≌△EBC（SAS）∴AD=EC。

等腰三角形中线练习题一、选择题1. 在等腰三角形ABC中，AB=AC，若AD是BC的中线，则下列结论正确的是：A. ∠BAD=∠CADB. ∠BAD=∠BACC. ∠CAD=∠BACD. ∠BAD=∠B2. 在等腰三角形ABC中，AB=AC，若AD是BC的中线，则下列结论正确的是：A. AD垂直于BCB. AD平行于BCC. AD=BCD. AD=AB3. 在等腰三角形ABC中，AB=AC，若AD是BC的中线，则下列结论正确的是：A. ∠BAD=∠CADB. ∠BAD=∠BACC. ∠CAD=∠BACD. ∠BAD=∠B4. 在等腰三角形ABC中，AB=AC，若AD是BC的中线，则下列结论正确的是：A. AD垂直于BCB. AD平行于BCC. AD=BCD. AD=AB5. 在等腰三角形ABC中，AB=AC，若AD是BC的中线，则下列结论正确的是：A. ∠BAD=∠CADB. ∠BAD=∠BACC. ∠CAD=∠BACD. ∠BAD=∠B二、填空题1. 在等腰三角形ABC中，AB=AC，若AD是BC的中线，则∠BAD=__________。

2. 在等腰三角形ABC中，AB=AC，若AD是BC的中线，则AD=__________。

3. 在等腰三角形ABC中，AB=AC，若AD是BC的中线，则∠BAC=__________。

4. 在等腰三角形ABC中，AB=AC，若AD是BC的中线，则∠BAD=__________。

5. 在等腰三角形ABC中，AB=AC，若AD是BC的中线，则AD=__________。

三、解答题1. 已知等腰三角形ABC中，AB=AC，AD是BC的中线，求证：∠BAD=∠CAD。

2. 已知等腰三角形ABC中，AB=AC，AD是BC的中线，求证：AD垂直于BC。

3. 已知等腰三角形ABC中，AB=AC，AD是BC的中线，求证：AD=AB。

4. 已知等腰三角形ABC中，AB=AC，AD是BC的中线，求证：∠BAD=∠BAC。

等腰三角形的练习题一、选择题1. 等腰三角形的两边相等，这个性质称为（）A. 对称性B. 等边性C. 等腰性D. 等角性2. 在等腰三角形中，底角相等的原因是（）A. 三角形内角和定理B. 等腰三角形的性质C. 相似三角形的判定D. 直角三角形的性质3. 等腰三角形的底边高等于腰上的高，这是因为（）A. 直角三角形的斜边中线性质B. 等腰三角形的三线合一性质C. 勾股定理D. 相似三角形的性质4. 已知等腰三角形的顶角为60°，那么这个三角形是（）A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定5. 如果等腰三角形的底边长为10厘米，腰长为13厘米，那么其面积是（）A. 30平方厘米B. 65平方厘米C. 100平方厘米D. 无法计算二、填空题6. 等腰三角形的两个底角相等，其大小为______。

7. 如果等腰三角形的顶角为120°，那么底角的大小为______。

8. 在等腰三角形ABC中，AB=AC，如果AB边上的高为h，那么AC边上的高也是______。

9. 等腰三角形的三线合一性质指的是______、______和______在同一直线上。

10. 如果等腰三角形的腰长为x，底边长为y，且x>y，那么面积公式为S=______。

三、解答题11. 已知等腰三角形的顶角为40°，求其底角的大小。

12. 一个等腰三角形的底边长为8厘米，腰长为10厘米，求其面积。

13. 证明：等腰三角形的底边上的中线、高线和角平分线重合。

14. 如果一个三角形的两边相等，且这两边所夹的角为70°，求这个三角形的另外两个内角的大小。

15. 已知等腰三角形的周长为32厘米，底边长为10厘米，求其腰长。

四、应用题16. 一个等腰三角形的花园，其底边长为20米，腰长为13米。

如果需要在花园的周围铺设一圈围栏，问需要多少米的围栏？17. 在一个等腰三角形ABC中，AB=AC，AB边上的高为h，求证：AC边上的高也是h。

等腰三角形练习题一、计算题：A1.如图，△ ABC中，AB=AC,BC=BD,AD=DE=EB求∠ A 的度数DE2. 如图， CA=CB,DF=DB,AE=AD B C F求∠ A 的度数CEA BD3、AB于⊥ AB于 E，DF⊥BC交 AC于点 F，若∠ EDF=70°，求∠ AFD的度数AFEB D C4. 如图，△ ABC 中， AB=AC,BC=BD=ED=EAA求∠ A 的度数EDBC5. 如图，△ ABC 中， AB=AC ，D 在 BC 上,A∠ B AD=30°, 在 AC 上取点 E ，使 AE=AD,求∠ EDC 的度数30°EBDC6. 如图，△ ABC 中，∠ C=90°， D 为 AB 上一点，作 DE ⊥BC 于 E ，若1BE=AC,BD=2,DE+BC=1,求∠ ABC 的度数ADCB7.如图，△ ABC中，AD均分∠ BAC，若AC=AB+BD求∠ B：∠ C的值AB D C二、证明题：8.如图，△ DEF中，∠ EDF=2∠E，FA⊥DE于点A，问：DF、AD、AE间有什么样的大小关系DAE F9.如图，△ ABC中，∠ B=60°，角均分线 AD、CE交于点 O求证： AE+CD=AC BE DA C12. 如图 , △ABC 中,AB=AC,D 为△ ABC 外一点，且∠ ABD=∠ACD =60°A求证： CD=AB-BDBDC13. 已知：如图， AB=AC=BE ，CD 为△ ABC 中 AB 边上的中线1A求证： CD=2CEDBCE14. 如图，△ ABC 中，∠ 1=∠2，∠ EDC=∠BACA求证： BD=ED1 2EBCD15. 如图，△ ABC中， AB=AC,BE=CF,EF交 BC于点 GA求证： EG=FGECBG F16. 如图，△ABC中，∠ABC=2∠C，AD是 BC边上的高， B 到点 E，使 BE=BD 求证： AF=FCAFBDCE17. 如图，△ ABC中， AB=AC,AD和 BE两条高，交于点 H，且 AE=BE求证： AH=2BD AEHB D C18. 如图，△ ABC中， AB=AC, ∠BAC=90°,BD=AB, ∠ABD=30°求证： AD=DCADB C19.如图，等边△ ABC中，分别延伸 BA至点 E，延伸 BC至点 D，使 AE=BD 求证： EC=ED EABC D20.如图，四边形 ABCD中，∠ BAD+∠BCD=180°，AD、BC的延伸线交于点F，DC、 AB的延伸线交于点E，∠ E、∠ F 的均分线交于点H求证： EH⊥FHFDCHABE一、计算题：1. 如图，△ ABC中，AB=AC,BC=BD,AD=DE=EB求∠ A 的度数A设∠ ABD为 x, 则∠ A 为 2x2x由 8x=180°D 得∠ A=2x=45°E 2xx3xx2. 如图， CA=CB,DF=DB,AE=ADB 2x3xC 求∠ A 的度数F设∠ A 为 x, XC由 5x=180°E得∠ A=36°2xxA x2x BD3.如图，△ ABC中，AB=AC，D在BC上，DE⊥AB于E，DF⊥BC交AC于点F，若∠ EDF=70°，求∠ AFD的度数∠A FD=160°AFEB D C4. 如图，△ ABC 中， AB=AC,BC=BD=ED=EAA求∠ A 的度数x设∠ A 为 x180E∠A=72xx2xD3x x3x BC5. 如图，△ ABC 中， AB=AC ，D 在 BC 上,∠ B AD=30°, 在 AC 上取点 E ，使 AE=AD,求∠ EDC 的度数设∠ ADE 为 xA∠EDC=∠AED －∠ C=15°180°－2x30°x －15°x Ex BDCx －15°6. 如图，△ ABC 中，∠ C=90°， D 为 AB 上一点，作 DE ⊥BC 于 E ，若1BE=AC,BD=2,DE+BC=1,求∠ ABC 的度数延伸 DE 到点 F, 使 EF=BC可证得 : △ABC ≌△ BFE所以∠ 1=∠F由∠ 2+∠F=90°,得∠ 1+∠F=90°1ADC E12B在 Rt △DBF 中, BD= 2,DF=1F所以∠ F = ∠1=30°7. 如图，△ ABC 中， AD 均分∠ BAC ，若 AC=AB+BD求∠ B ：∠ C 的值在 AC 上取一点 E, 使 AE=AB A可证△ ABD ≌△ ADE所以∠ B=∠AEDEB D C由AC=AB+BD,得 DE=EC,所以∠ AED=2∠C 故∠ B：∠ C=2:1二、证明题：8.如图，△ ABC中，∠ ABC,∠CAB的均分线交于点P，过点 P 作 DE∥AB，分别交 BC、AC于点 D、E求证： DE=BD+AEC证明△ PBD和△ PEA是等腰三角形 D P EB A9.如图，△ DEF中，∠ EDF=2∠E，FA⊥DE于点A，问：DF、AD、AE间有什么样的大小关系DDF+AD=AE A在 AE上取点 B, 使 AB=ADBE F10.如图，△ ABC中，∠ B=60°，角均分线 AD、CE交于点 O求证： AE+CD=AC B在 AC上取点 F, 使 AF=AE易证明△ AOE≌△ AOF, E DO得∠ AOE=∠AOF由∠ B=60°，角均分线 AD、CE,A F C得∠ AOC=120°所以∠ AOE=∠AOF=∠COF=∠COD=60°故△ COD≌△ COF,得 CF=CD所以 AE+CD=AC11. 如图，△ ABC中， AB=AC, ∠A=100°， BD均分∠ ABC,求证： BC=BD+AD延伸 BD到点 E, 使 BE=BC,连接 CE A在 BC上取点 F, 使 BF=BA D E 易证△ ABD≌△ FBD,得 AD=DF再证△ CDE≌△ CDF,得 DE=DF BF CA故 BE=BC=BD+ADD也可 : 在 BC上取点 E, 使 BF=BD,连接 DF在 BF 上取点 E, 使 BF=BA,连接 DEB先证 DE=DC,再由△ ABD≌△ EBD,得 AD=DE,最后证明 DE=DF即可 E FC 12. 如图 , △ABC中,AB=AC,D为△ ABC外一点，且∠ ABD=∠ACD =60°求证： CD=AB-BD AE在 AB上取点 E，使 BE=BD，在 AC上取点 F，使 CF=CDF得△ BDE与△ CDF均为等边三角形，DB只要证△ ADF≌△ AEDC13. 已知：如图， AB=AC=BE ，CD 为△ ABC 中 AB 边上的中线1A求证： CD=2CEE延伸 CD 到点 E, 使 DE=CD 连.结 AED证明△ ACE ≌△ BCEBC14. 如图，△ ABC 中，∠ 1=∠2，∠ EDC=∠BAC E求证： BD=EDA 1 2在 CE 上取点 F, 使 AB=AFEF易证△ ABD ≌△ ADF,得 BD=DF,∠B=∠AFDBCD由∠ B+∠BAC+∠C=∠DEC+∠EDC+∠C=180°所以∠ B=∠DEC所以∠ DEC=∠AFD所以 DE=DF,故 BD=ED15. 如图，△ ABC 中， AB=AC,BE=CF,EF 交 BC 于点 GA求证： EG=FGECBGF16. 如图，△ABC中，∠ABC=2∠C，AD是 BC边上的高， B 到点 E，使 BE=BD 求证： AF=FC AFB17.如图，△ ABC中， AB=AC,AD和 BE两条高，交E于点求证： AH=2BD由△ AHE≌△ BCE,得 BC=AH18. 如图，△ ABC中， AB=AC, ∠BAC=90°,BD=AB,∠ABD=30°求证： AD=DC作AF⊥BD于 F,DE⊥AC于 E可证得∠ DAF=DAE=15°,所以△ ADE≌△ ADF B得AF=AE,由AB=2AF=2AE=AC,DH，且 AE=BEAHB DAEFDCCEC所以 AE=EC,所以 DE是 AC的中垂线 , 所以 AD=DC19. 如图，等边△ ABC 中，分别延伸 BA 至点 E ，延伸 BC 至点 D ，使 AE=BD求证： EC=EDE延伸 BD 到点 F, 使 DF=BC,A可得等边△ BEF,BCD F只要证明△ BCE ≌△ FDE 即可20. 如图，四边形 ABCD 中，∠ BAD+∠BCD=180°，AD 、BC 的延伸线交于点F ，DC 、 AB 的延伸线交于点 E ，∠ E 、∠ F 的均分线交于点 H求证： EH ⊥FHF延伸 EH 交 AF 于点 G由∠ BAD+∠BCD=180° ,∠DCF+∠BCD=180° D得∠ BAD=∠DCF,CG1由外角定理 , 得∠ ∠2 MH1= 2,故△ FGM 是等腰三角形ABE由三线合一 , 得 EH ⊥。

中考数学总复习《等腰三角形》专项提升练习题(附答案) 学校:___________班级：___________姓名：___________考号：___________一、选择题1.若一个等腰三角形的两边长分别是2和5，则它的周长为( )A.12B.9C.12或9D.9或72.若等腰三角形的顶角为40°，则它的底角度数为( )A.40°B.50°C.60°D.70°3.如图，在等腰三角形ABC中，AB＝AC，BD平分∠ABC，∠A＝36°，则∠1的度数为( )A.36°B.60°C.72°D.108°4.如图，在△ABC中，D为BC的中点，AD⊥BC，E为AD上一点，∠ABC＝60°，∠ECD＝40°，则∠ABE＝( )A.10°B.15°C.20°D.25°5.如图，在△ABC中，AB＝AC，点D、E在BC上，连接AD、AE，如果只添加一个条件使∠DAB＝∠EAC，则添加的条件不能为( )A.BD＝CEB.AD＝AEC.DA＝DED.BE＝CD6.等腰三角形补充下列条件后，仍不一定成为等边三角形的是( )A.有一个内角是60°B.有一个外角是120°C.有两个角相等D.腰与底边相等7.等边△ABC的两条角平分线BD和CE相交所夹锐角的度数为( )A.60°B.90°C.120°D.150°8.如图，等边△OAB的边长为2，则点B的坐标为( )A.(1，1)B.(3，1)C.(3，3)D.(1，3)9.如图，△ABC中∠A=30°，E是AC边上的点，先将△ABE沿着BE翻折，翻折后△ABE的AB边交AC于点D，又将△BCD沿着BD翻折，C点恰好落在BE上，此时∠CDB=82°，则原三角形的∠B为( )A.75°B.76°C.77°D.78°10.如图，在△ABC中，AB＝AC，D、E是△ABC内的两点，AD平分∠BAC，∠EBC＝∠E＝60°，若BE＝6 cm，DE＝2 cm，则BC的长为( )A.4 cmB.6 cmC.8 cmD.12 cm二、填空题11.等腰三角形的一个内角为100°，则顶角的度数是________．12.如图，已知△ABC的角平分线CD交AB于D，DE∥BC交AC于E，若DE＝3，AE＝4，则AC＝.13.如图，l∥m，等边△ABC的顶点B在直线m上，∠1＝20°，则∠2的度数为.14.如图所示，△ABC为等边三角形，AD⊥BC，AE＝AD，则∠ADE＝________.15.已知一张三角形纸片ABC(如图甲)，其中AB＝AC．将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为BD(如图乙)．再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为EF(如图丙)．原三角形纸片ABC中，∠ABC的大小为．16.《蝶几图》是明朝人戈汕所作的一部组合家具的设计图(蜨，同“蝶”)，如图为某蝶几设计图，其中△ABD和△CBD为“大三斜”组件(大三斜组件为两个全等的等腰直角三角形)，已知某人位于点P处，点P与点A关于直线DQ对称，连接CP、DP.若∠ADQ＝25°，则∠DCP的度数为.三、解答题17.如图，在△ABC中，AC＝DC＝DB，∠ACD＝100°，求∠B的度数.18.如图，△ABC中，AC＝BC，点D在BC上，作∠ADF＝∠B，DF交外角∠ACE的平分线CF于点F.（1）求证：CF∥AB；（2）若∠CAD＝20°，求∠CFD的度数.19.如图，等边△ABC中，AD是∠BAC的角平分线，E为AD上一点，以BE为一边且在BE下方作等边△BEF，连接CF.(1)求证：AE＝CF；(2)求∠ACF的度数.20.如图，△ABC是等边三角形，D、E、F分别是AB、BC、AC上一点，且∠DEF＝60°.(1)若∠1＝50°，求∠2；(2)连接DF，若DF∥BC，求证：∠1＝∠3.21.如图，在△ABC中，AB＝BC，CD⊥AB于点D，CD＝BD，BE平分∠ABC，点H是BC 边的中点，连接DH，交BE于点G，连接CG．(1)求证：△ADC≌△FDB；(2)求证：CE＝12BF；(3)判断△ECG的形状，并证明你的结论；22.如图，已知在等边三角形ABC中，点D、E分别在直线AB、直线AC上，且AE＝BD．(1)当点D、E分别在边AC、边AB上时，如图1所示，EB与CD相交于点G，求∠CGE 的度数；(2)当点D、E分别在边CA、边AB的延长线上时，如图2所示，∠CGE的度数是否变化？如不变，请说明理由．如变化，请求出∠CGE的度数．答案1.A2.D3.C4.C.5.C6.C7.A8.D9.D10.C.11.答案为：100°.12.答案为：7.13.答案为：40°.14.答案为：75°15.答案为：72°.16.答案为：20°.17.解：∵AC＝DC＝DB，∠ACD＝100°∴∠CAD＝(180°﹣100°)÷2＝40°∵∠CDB是△ACD的外角∴∠CDB＝∠A＋∠ACD＝100°＝40°＋100°＝140°∵DC＝DB∴∠B＝(180°﹣140°)÷2＝20°.18.（1）证明：∵AC＝BC∴∠B＝∠BAC∵∠ACE＝∠B+∠BAC∴∠BAC＝12∠ACE∵CF平分∠ACE∴∠ACF＝∠ECF＝12∠ACE∴∠BAC ＝∠ACF∴CF ∥AB ；（2）解：∵∠BAC ＝∠ACF ，∠B ＝∠BAC ，∠ADF ＝∠B ∴∠ACF ＝∠ADF∵∠ADF+∠CAD+∠AGD ＝180°，∠ACF+∠F+∠CGF ＝180° 又∵∠AGD ＝∠CGF∴∠F ＝∠CAD ＝20°.19.证明：(1)∵△ABC 是等边三角形∴AB ＝BC ，∠ABE ＋∠EBC ＝60°.∵△BEF 是等边三角形∴EB ＝BF ，∠CBF ＋∠EBC ＝60°.∴∠ABE ＝∠CBF.在△ABE 和△CBF 中⎩⎨⎧AB ＝BC ，∠ABE ＝∠CBF EB ＝BF ，∴△ABE ≌△CBF(SAS).∴AE ＝CF.(2)∵等边△ABC 中，AD 是∠BAC 的角平分线∴∠BAE ＝30°，∠ACB ＝60°.∵△ABE ≌△CBF∴∠BCF ＝∠BAE ＝30°.∴∠ACF ＝∠BCF ＋∠ACB ＝30°＋60°＝90°.20.解：(1)∵△ABC 是等边三角形∴∠B ＝∠A ＝∠C ＝60°∵∠B ＋∠1＋∠DEB ＝180°∠DEB ＋∠DEF ＋∠2＝180°∵∠DEF ＝60°∴∠1＋∠DEB ＝∠2＋∠DEB∴∠2＝∠1＝50°；(2)连接DF∵DF∥BC∴∠FDE＝∠DEB∵∠B＋∠1＋∠DEB＝180°，∠FDE＋∠3＋∠DEF＝180°∵∠B＝60°，∠DEF＝60°∴∠1＝∠3.21.证明：(1)∵AB＝BC，BE平分∠ABC∴BE⊥AC，CE＝AE∵CD⊥AB∴∠ACD＝∠DBF在△ADC和△FDB中∴△ADC≌△FDB(ASA)；(2)∵△ADC≌△FDB∴AC＝BF又∵CE＝AE∴CE＝12BF；(3)△ECG为等腰直角三角形．∵点H是BC边的中点∴GH垂直平分BC∴GC＝GB∵∠DBF＝∠GBC＝∠GCB＝∠ECF，得∠ECG＝45°又∵BE⊥AC∴△ECG为等腰直角三角形.22.(1)证明：∵△ABC为等边三角形∴AB＝BC，∠A＝∠ABC＝60°在△ABE和△BCD中AE＝BD,∠A＝∠DBC,AB＝BC∴△ABE≌△BCD∴∠ABE＝∠BCD∵∠ABE＋∠CBG＝60°∴∠BDG＋∠CBG＝60°∵∠CGE＝∠BCG＋∠CBG∴∠CGE＝60°；(2)证明：∵△ABC为等边三角形∴AB＝BC，∠CAB＝∠ABC＝60°∴∠EAB＝∠CBD＝120°在△ABE和△BCD中AB＝BC,∠EAB＝∠CBD,AE＝BD∴△ABE≌△BCD(SAS)∴∠D＝∠E∵∠ABE＝∠DBG，∠CAB＝∠E＋ABE＝60°∴∠CGE＝∠D＋∠DBG＝60°．。

练习一一、选择题1．等腰三角形的周长为26㎝，一边长为6㎝，那么腰长为（）Ａ．6㎝Ｂ．10㎝Ｃ．6㎝或10㎝Ｄ．14㎝2．已知△ABC，AB =AC，∠B=65°，∠C度数是( )A．50°B．65°C．70°D．75°3．等腰三角形是轴对称图形，它的对称轴是（）A．过顶点的直线B．底边的垂线C．顶角的平分线所在的直线D．腰上的高所在的直线二、填空题4．等腰三角形的两个_______相等（简写成“____________”）．5．已知△ABC，AB =AC，∠A=80°，∠B度数是_________．6．等腰三角形的两个内角的比是1：2，则这个等腰三角形的顶角的度数是_______________．7．等腰三角形的腰长是6，则底边长5，周长为__________．三、解答题8．如图AB=AD，AD∥BC，求证：BD平分∠ABC．（写出每步证明的重要依据）9．如图，在△ABC中，AB=AC，D、E分别在AC、AB边上，且BC=BD，AD=DE=EB，求∠A的度数一、选择题1．B2．B3．C二、填空题4．底角，等边对等角5．50°6．36°或90°7．16或17三、解答题8．如图AB=AD，AD∥BC，求证：BD平分∠ABC．证明：∵AB=AD（已知）∴∠ABD=∠ADB（等边对等角）∵AD∥BC（已知）∴∠ADB=∠CBD（两直线平行，内错角相等）∴∠ABD=∠CBD（等量代换）∴BD平分∠ABC．（角平分线定义）9．45练习2一、选择题1．△ABC是等边三角形，D、E、F为各边中点，则图中共．有正三角形( )A．2个B．3个C．4个D．5个2．△ABC中，∠A：∠B：∠C=1：2：3，则BC：AB等于( )A．2：1 B．1：2 C．1：3 D．2 ：3二、填空题3．等边三角形的周长为6㎝，则它的边长为________．4．等边三角形的两条高线相交所成钝角的度数是__________．5．在△ABC中，∠A=∠B=∠C，则△ABC是_____三角形．6．△ABC中，∠AC B=90°∠B=60°，BC=3㎝，则AB=_______．三、解答题7．△ABC是等边三角形，点D在边BC上，DE∥AC，△BDE是等边三角形吗？试说明理由．8．已知：如图，P，Q是△ABC边上BC上的两点，且BP=PQ=QC=AP=AQ，求∠BAC的度数．9．已知：△ABC中，∠ACB=90°，AD=BD，∠A=30°，求证：△BDC是等边三角形．一、选择题1．D2．B二、填空题3．2㎝4．120°5．等边6．6㎝三、解答题7．△ABC是等边三角形．理由是∵△ABC是等边三角形AQ CPB∴∠A =∠B =∠C=60° ∵DE ∥AC ，∴∠BED =∠A=60°，∠BDE =∠C =60° ∴∠B =∠BED =∠BDE ∴△ABC 是等边三角形 8．∠BAC=120°9．证明：∵△ABC 中，∠ACB=90°，∠A=30°（已知）∴∠A +∠B=90°（直角三角形两锐角互余） ∴∠B= 90°－∠A= 90°－30°=60° ∵△ABC 中，∠ACB=90°，∠A=30°（已知） ∴BC=（在直角三角形中，一个锐角等于30，那么它所对的直角边等于斜边的一半）∴△BDC 是等边三角形（有一个角是60°角的等腰三角形是等边三角形）。