3.2推导长正方体的体积计算方法

人教版五年级数学下册同步重难点知识点第三单元长方体和正方体的体积温馨提示：图片放大更清晰！1.掌握长方体、正方体的特征，认识各个部分的名称。

2.掌握长方体和正方体的表面积的计算方法。

3.理解体积的概念，掌握体积单位及体积单位之间的进率，能正确进行单位的换算。

4.掌握长方体和正方体体积的计算方法。

5.掌握容积的意义、容积单位间的进率及容积单位与体积单位的换算。

6.会计算不规则物体的体积。

重点：1.长方体、正方体的特征。

2.长方体、正方体表面积和体积的计算方法。

难点：用公式解决生活中的实际问题。

知识点一：认识长方体长方体是由六个长方形（特殊情况下有两个相对的面是正方形）围成的立体图形。

一个长方体有6个面，相对的面完全相同；有12条棱，相对的棱长度相等；有8个顶点。

知识点二：认识正方体正方体是（也叫立方体）是由六个完全相同的正方形围成的立体图形。

一个正方体有6个面，每个面完全相同；有12条棱，每条棱长度相等；有8个顶点。

知识点三：长方体、正方体的展开图长方体和正方体的展开图都有多种。

利用长方体和正方体的展开图可以探究各个面之间的关系。

知识点四：长方体、正方体表面积的计算长方体或正方体6个面的总面积，叫做它的表面积。

长方体的表面积：（长×宽+长×高+宽×高）×2正方体的表面积：棱长×棱长×6知识点五：体积和体积单位物体所占空间的大小叫做物体的体积。

计量体积要用体积单位，常用的体积单位有立方厘米、立方分米和立方米，可以分别写成cm³、dm³和m³。

知识点六：长方体、正方体体积公式的推导长方体的体积=长×宽×高 V = abh正方体的体积=棱长×棱长×棱长 V = a3知识点七：长方体、正方体体积公式的应用长方体或正方体底面的面积叫底面积。

长方体或正方体的体积=底面积×高V = Sh知识点八：体积单位间的进率1dm³=1000cm ³ 1m³=1000dm³高级单位转换成为低级单位，用乘法进率，小数点向右移；低级单位转化成高级单位，用除法进率，小数点向左移。

用举例法写出长方体体积公式的推导过程好的，以下是为您生成的文章：咱们在学习数学的时候，经常会碰到各种各样的公式，其中长方体体积公式就是很重要的一个。

那这个公式到底是咋来的呢？今天咱们就来好好说道说道。

先来说说啥是长方体，您就想象一下，家里的鞋盒子、装牛奶的纸箱子，那些方方正正的，有长、宽、高的家伙，就是长方体。

那长方体的体积咋算呢？咱们来举个例子。

比如说，有一个长方体的盒子，长是 5 厘米，宽是 3 厘米，高是 2 厘米。

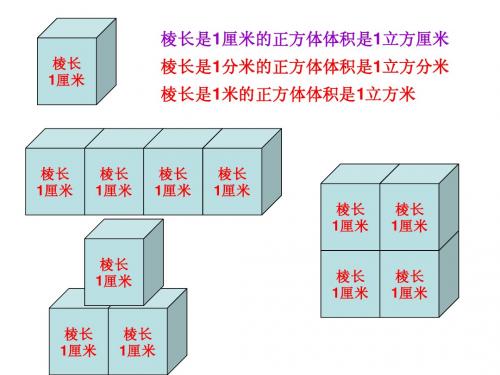
咱们可以把这个长方体想象成是用一个个小正方体拼成的。

就像搭积木一样，一个小正方体就是一个体积单位。

那咱们先沿着长摆，能摆几个小正方体呢？因为长是 5 厘米，而小正方体的边长咱们假设是 1 厘米，所以沿着长能摆 5 个。

再沿着宽摆，能摆几排呢？宽是 3 厘米，所以能摆 3 排。

最后沿着高摆，能摆几层呢？高是 2 厘米，所以能摆 2 层。

那这样一来，这个长方体盒子里面一共就有 5×3×2 = 30 个小正方体。

而每个小正方体的体积是 1×1×1 = 1 立方厘米，所以这个长方体盒子的体积就是 30 立方厘米。

通过这个例子咱们就能发现，长方体的体积其实就是长×宽×高。

我记得有一次，我带着我家小侄子做数学作业，就碰到了求长方体体积的题目。

这小家伙一开始怎么都不明白，我就拿了一堆积木块给他演示。

我跟他说：“你看啊，这就像咱们盖房子，长就相当于房子的长度，宽就是房子的宽度，高就是房子的高度。

咱们一层一层地盖，最后算出来总的积木块数量，就是这个长方体的体积。

”小侄子瞪着大眼睛，似懂非懂地点点头。

然后我让他自己动手摆一摆，他摆弄了一会儿，突然兴奋地喊：“姑姑，我懂啦！”那一刻，我心里别提多有成就感了。

所以啊，咱们学习长方体体积公式，通过这样的举例就能很清楚地明白其中的道理。

以后再遇到求长方体体积的问题，就不会头疼啦！不管是在生活中，还是在学习里，咱们多观察、多动手，很多难题就能迎刃而解。

长方体和正方体的表面积和体积公式的推导
过程
长方体的表面积和体积公式是：
表面积= 2lw + 2lh + 2wh
体积= lwh
其中，l代表长，w代表宽，h代表高。

推导过程是，首先考虑长方体的六个面，分别有长宽、长高和宽
高组成，所以长方体的表面积可以表示为所有这些面积的总和，即2lw + 2lh + 2wh。

而长方体的体积可以看作是长方体的底面积乘以高，因此体积等
于lwh。

接下来，我们来推导正方体的表面积和体积公式。

正方体的特点
是长、宽、高都相等，设边长为a。

根据正方体的定义，它有六个面，每个面的面积都是a^2。

因此，正方体的表面积为6a^2。

正方体的体积可以看作是正方体的底面积a^2乘以高，因此体积等于a^3。

总结来说，长方体的表面积和体积公式可以直接通过面积和体积的定义进行推导。

而正方体只是长方体的特殊情况，所以推导方法与长方体类似，只是边长相等而已。

拓展：以上是针对长方体和正方体的简单情况推导的表面积和体积公式。

对于其他几何体，比如球体、圆柱体、圆锥体，也有各自的表面积和体积公式，并且推导方法也各有不同。

感兴趣的读者可以进一步了解和了解其他几何体的表面积和体积公式。

长长方体体积推导公式在我们的数学世界里，长方体体积的推导公式就像是一把神奇的钥匙，能打开好多知识的大门。

还记得我上小学的时候，有一次数学课上，老师拿着一个用卡纸做的长方体模型走进教室。

那个长方体做得特别精致，棱边整整齐齐的，面上还涂着不同的颜色。

老师把它放在讲桌上，笑着问我们：“同学们，你们猜猜这个长方体里面能装多少东西呀？”大家都一脸懵，不知道该怎么回答。

然后老师就开始给我们讲长方体体积的推导啦。

老师先在黑板上画了一个大大的长方体，标上了长、宽、高。

她说：“咱们来把这个长方体想象成一个装满了小正方体的盒子。

”说着，她就在黑板上开始画小正方体。

“假如这个小正方体的边长是 1 厘米，那沿着长方体的长能摆几个小正方体呀？”老师指着黑板上的图问我们。

同学们纷纷举手回答，经过一番讨论，我们得出沿着长能摆的小正方体个数就是长方体长的长度（单位：厘米）。

接着老师又问：“那沿着宽能摆几个呢？”同样的，我们又算出了沿着宽能摆的小正方体个数就是长方体宽的长度（单位：厘米）。

“那沿着高呢？”老师的问题一个接一个。

最后我们发现，沿着高能摆的小正方体个数就是长方体高的长度（单位：厘米）。

这时，老师笑着说：“那你们想想，这个长方体里一共能摆多少个小正方体呀？”大家恍然大悟，原来长方体体积就等于长×宽×高呀！因为小正方体的体积是 1 立方厘米，所以长方体里小正方体的个数，也就是长方体的体积，就是长×宽×高啦。

从那以后，我对长方体体积的推导公式记得特别牢。

在生活中，也经常能用到这个知识呢。

比如我帮妈妈整理衣柜的时候，看到一个长方体形状的收纳盒，我就能很快算出它能装多少东西。

再后来上了初中、高中，数学变得越来越复杂，但长方体体积的推导公式始终是基础中的基础。

在做几何题的时候，它经常会派上用场。

其实呀，数学里的好多知识都是这样，从最基础最简单的开始，一点点变得越来越难，越来越深奥。

但只要我们把基础打牢，就像掌握了长方体体积的推导公式一样，再难的问题也能慢慢解决。

归纳长方体正方体圆柱圆锥体积公式推导过程
推导长方体、正方体、圆柱和圆锥的体积公式
长方体体积公式推导过程：
我们知道长方体的体积等于底面积乘以高度。

设长方体的底面积为S，高度为h，则长方体的体积V=S*h。

正方体体积公式推导过程：
正方体是长方体的特殊情况，即长宽高相等。

设正方体的一边长为a，则底面积为a*a=a^2，高度也为a，所以正方体的体积V=a^2*a=a^3。

圆柱体积公式推导过程：
圆柱的底面为圆形，设底面半径为r，高度为h。

圆柱的底面积为π*r^2，高度为h，所以圆柱的体积V=π*r^2*h。

圆锥体积公式推导过程：
圆锥的底面为圆形，设底面半径为r，高度为h。

圆锥的底面积为π*r^2，高度为h，所以圆锥的体积V=1/3*π*r^2*h。

通过以上推导过程，我们得出了长方体、正方体、圆柱和圆锥的体积公式。

这些公式在几何学和工程学中都有广泛的应用，可以帮助我们计算和解决各种实际问题。

深入理解这些公式的推导过程，有
助于我们更好地掌握数学知识，提高解决问题的能力。

希望这篇文章能帮助读者更好地理解和运用这些几何体积公式。