2014年数学必修4、必修5考试题(8)

2014年高一数学必修4考试题(6)DA. 重心B. 垂心C. 外心D. 内心二、填空题（本大题共4小题，每小题4分，共16分） 13. 函数1tan y x=-的定义域是 __________________________.14.函数2sin cos y x x=+的值域是________________________.15. 下面四个命题中，其中正确命题的序号为____________.① 函数()tan f x x =是周期为π的偶函数；② 若βα、是第一象限的角，且βα>，则βαsin sin >；③ 8π=x 是函数)452sin(π+=x y 的一条对称轴方程； ④ 在(,)22ππ-内方程tan sin x x =有3个解. 16. 在△ABC 中，AB = 4，AC = 3，60A ∠=，D 是AB 的中点，则CA CD ⋅=______.三、解答题（本大题共5小题，共48分） 17. （6分）已知点A (1,1)-，点B (1,2)，若点C 在直线3y x=上，且AB BC ⊥. 求点C 的坐标.18. （8分）已知sin()3sin()2()112cos()cos(5)2f παπααπαπα++--=---.（Ⅰ）化简()f α； （Ⅱ）已知tan 3α=，求()f α的值．19．（11分）已知向量(cos ,sin )a αα=，(cos ,sin )b ββ=，25a b -=． （Ⅰ）求cos()αβ-的值；（Ⅱ）若02πα<<，02πβ-<<，且5sin 13β=-，求sin α．20. （11分）已知向量(3,cos 2),(sin 2,1),(0)a xb x ωωω==>，令(),f x a b =⋅且)(x f 的周期为π．（Ⅰ）求函数()f x 的解析式；（Ⅱ）若[0,]2x π∈时()3f x m +≤，求实数m 的取值范围．21. （12分）已知函数()sin()f x A x ωϕ=+(0,0,)A ωϕπ>><，在同一周期内，当12x π=时，()f x 取得最大值3；当712x π=时，()f x 取得最小值3-.（Ⅰ）求函数()f x 的解析式； （Ⅱ）求函数()f x 的单调递减区间；（Ⅲ）若,36x ππ⎡⎤∈-⎢⎥⎣⎦时，函数()2()1h x f x m =+-有两个零点，求实数m 的取值范围．参考答案一、选择题（本小题共12小题，每小题3分，共36分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案D C B A B B C C A D D A二、填空题（本大题共4小题，每小题4分，共16分）13. (,]24k k k Zππππ-++∈ 14. 5[1,]4- 15. ①③ 16. 6三、 解答题（本大题共5小题，共48分） 17.【解析】设C （x ，3x ），则(2,1),(1,32)AB BC x x ==--44122(21)320(,)555x x x C ∴-+-=∴=∴ ……………6分18．【解析】（Ⅰ）cos 3sin ()2sin cos f ααααα+=-+ ……………4分 （Ⅱ）13tan 10()22tan 15f ααα+===--+- ……………8分 19．【解析】（Ⅰ）||1,||1a b == 又24||5a b -=432255a b a b ∴-⋅=∴⋅=即3cos cos sin sin 5αβαβ+=()3cos 5αβ∴-=……………5分（法二） (cos ,sin )a αα=， (cos ,sin )b ββ=，()cos cos sin sin a b αβαβ∴-=--，．25a b -=， ()()2225cos cos sin sin αβαβ-+-=，即 ()422cos 5αβ--=， ()3cos 5αβ∴-=．（Ⅱ）0,0,022ππαβαβπ<<-<<∴<-<，()3cos 5αβ-=， ()4sin .5αβ∴-=5sin 13β=-， 12cos 13β∴=，()()()sin sin sin cos cos sin 412353351351365ααββαββαββ∴=-+=-+-⎡⎤⎣⎦⎛⎫=⋅+⋅-= ⎪⎝⎭ (11)分20. 【解析】（Ⅰ）()3sin2cos22sin(2)6f x a b x x x πωωω=⋅=+=+ ∵)(x f 的周期为π ∴1=ω ()2sin(2)6f x x π∴=+ ……………5分 （Ⅱ） 0,2x π⎡⎤∈⎢⎥⎣⎦，则72,666x πππ⎡⎤+∈⎢⎥⎣⎦1sin(2)[,1]62x π∴+∈- ()[1,2]f x ∴∈- 231m m ∴+≤∴≤……………11分 21. 【解析】（Ⅰ）由题意，3A = 72(),1212T πππ=-= 2 2.T πω== ……2分由22122k ππϕπ⨯+=+ 得2,3k k Z πϕπ=+∈ 又,3ππϕπϕ-<<∴= ()3sin(2)3f x x π∴=+ ……4分 （Ⅱ）由3222232k x k πππππ+≤+≤+ 得722266k x k ππππ+≤≤+ 71212k x k k Z ππππ+≤≤+∈7(),]1212f x k k k Z ππππ∴++∈函数的单调递减区间为[ ……8分（Ⅲ）由题意知，方程1sin(2)36m x π-+=在,]36ππ[-上有两个根.2,]2,]36333x x πππππ∈∴+∈[-[-13,1)[331,7)6m m -∴∈∴∈ ……12分。

2014年高中第四册数学期末考试试卷答
案
2014年高中第四册数学期末考试试卷答案
【摘要】多了解一些考试资讯信息，对于学生和家长来讲非常重要，xx为大家整理了2014年高中第四册数学期末考试试卷答案一文，希望对大家有帮助。

一、DCABC;BBCCC;CD.
二、
13、14、2 15、21 16、
三、17.【解析】
18.【解析】
(Ⅰ) 2分
4分
5分
由得，( ).，7分
故的单调递增区间为( ). 8分
(Ⅱ) ,则9分
10分
又11分
12分
考点：三角函数的性质
点评：解决的关键是利用二倍角公式将表达式化为单一函数，同时能结合性质来得到结论，属于基础题。

19.【解析】(1) ;(2)
20.【解析】本题考查离散形随机变量及其分布列的求法，期望的求法，考查了等可能事件概率的求法公式，是一道应用概率解决实问题的应用题，此类题型随着高考改革的深入，在高考的试卷上出现的频率越来越高，应加以研究体会此类题的规范解法.
(1)求甲，乙两组各抽取的人数，根据分层的规则计算即可;
(2)从甲组抽取的工人中恰有1名女工这个事件表明是从甲组中抽取了一男一女，计算出总抽法的种数与)从甲组抽取的工人中恰有1名女工的种数，用古典概率公式即可求解;
(3)令X表示抽取的3名工人中男工人的人数，则X可取值：0，1，2，3，依次算出每和种情况的概率，列出分布列，据公式求出其期望值即可.
解：(1)
答：从甲组抽取2名，从乙组抽取1名
(2)从甲组抽取的工人中恰有1名女工的概率为
(3)X可取值：0，1，2，3
X的分布列为。

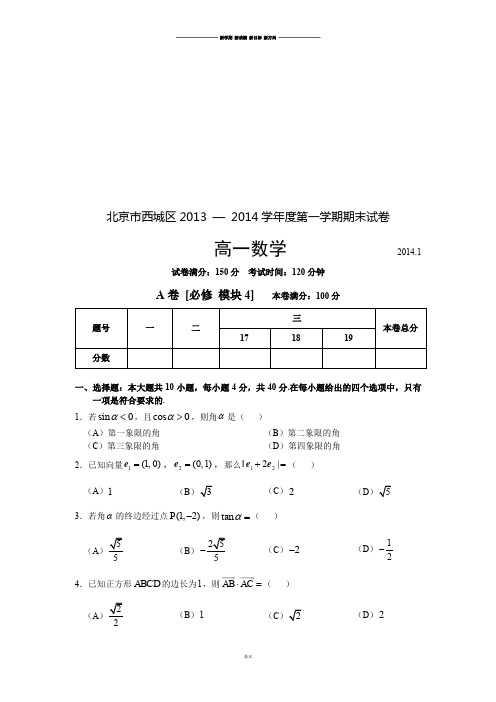
北京市西城区2013 — 2014学年度第一学期期末试卷高一数学 2014.1试卷满分：150分 考试时间：120分钟A 卷 [必修 模块4] 本卷满分：100分题号 一 二三本卷总分1718 19 分数一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的. 1．若sin 0<α，且cos 0>α，则角α是（ ） （A ）第一象限的角 （B ）第二象限的角 （C ）第三象限的角（D ）第四象限的角2．已知向量1(1,0)=e ，2(0,1)=e ，那么122|+=|e e （ ） （A ）1（B ）3（C ）2（D ）53．若角α的终边经过点(1,2)P -，则tan =α（ ）（A ）55（B ）255-（C ）2- （D ）12-4．已知正方形ABCD 的边长为1，则AB AC ⋅=（ ） （A ）22（B ）1（C ）2（D ）25．在平面直角坐标系xOy 中，函数2sin()6y x π=-的图象（ ） （A ）关于直线6x π=对称 （B ）关于直线6x π=-对称 （C ）关于点(,0)6π对称（D ）关于点(,0)6π-对称 6．已知非零向量,OA OB 不共线，且13BM BA =，则向量OM =（ ） （A ）1233OA OB +（B ）2133OA OB +（C ）1233OA OB -（D ）1433OA OB -7．已知函数31()sin cos 22f x x x =+，则()12f π=（ ） （A ）22 （B ）32（C ）1（D ）28．设a ，b 是两个非零向量，且+=-a b a b ，则a 与b 夹角的大小为（ ） （A ）120︒（B ）90︒（C ）60︒（D ）30︒9．已知函数()sin cos f x x x =ωω在区间[,]63ππ-上单调递增，则正数ω的最大值是（ ） （A ）32（B ）43（C ）34 （D ）2310．已知函数()cos(sin )f x x =，则下列结论中正确的是（ ） （A ）()f x 的定义域是[1,1]- （B ）()f x 的值域是[1,1]- （C ）()f x 是奇函数（D ）()f x 是周期为π的函数二、填空题：本大题共6小题，每小题4分，共24分. 把答案填在题中横线上. 11. sin()6π-=______.12. 若3sin 2=α，且(0,)∈πα，则α=______. 13. 已知向量(1,3)=a ，(2,)k =-b ．若向量a 与b 共线，则实数k =_____. 14. 若tan 2=α，且32π∈(π,)α，则sin()2π+=α______.15. 已知向量(cos ,sin )αα=a ，(cos ,sin )ββ=b ．若π,3〈〉=a b ，则c o s ()-=αβ_____. 16. 定义在R 上的非常值函数()f x 同时满足下述两个条件：① 对于任意的x ∈R ，都有2()()3f x f x π+=； ② 对于任意的x ∈R ，都有()()66f x f x ππ-=+.则其解析式可以是()f x =_____.（写出一个满足条件的解析式即可）三、解答题：本大题共3小题，共36分.解答应写出文字说明，证明过程或演算步骤. 17. （本小题满分12分）已知3tan 4=-α. （Ⅰ）求πtan()4-α的值； （Ⅱ）求2sin 3cos 3sin 2cos --αααα的值.18.（本小题满分12分）已知函数2()sin 23sin 2cos 2f x x x x =+⋅．（Ⅰ）求()f x 的最小正周期；（Ⅱ）若[,]84x ππ∈，求()f x 的最大值与最小值．19.（本小题满分12分）如图，正六边形ABCDEF 的边长为1.,M N 分别是,BC DE 上的动点，且满足BM DN =.（Ⅰ）若,M N 分别是,BC DE 的中点，求AM AN ⋅的值； （Ⅱ）求AM AN ⋅的取值范围.B 卷 [学期综合] 本卷满分：50分一、填空题：本大题共5小题，每小题4分，共20分.把答案填在题中横线上. 1. 已知集合2{|430}A x x x =-+>，{|02}B x x =<≤，那么A B =_____.2. 已知2log 3a =，32b=，21log 3c =.将,,a b c 按从小到大排列为_____. 3. 若函数2()2f x x x =-在区间(,)a +∞上是增函数，则a 的取值范围是_____. 4. 函数12()|21|xf x x =--的零点个数为_____.5. 给定数集A .若对于任意,a b A ∈，有a b A +∈，且a b A -∈，则称集合A 为闭集合.给出如下四个结论：① 集合{4,2,0,2,4}A =--为闭集合； ② 集合{|3,}A n n k k ==∈Z 为闭集合； ③ 若集合12,A A 为闭集合，则12A A 为闭集合；④ 若集合12,A A 为闭集合，且1A R Ø，2A R Ø，则存在c ∈R ，使得12()c A A ∉.其中，全部正确结论的序号是_____.二、解答题：本大题共3小题，共30分.解答应写出文字说明，证明过程或演算步骤. 6.（本小题满分10分）题号 一 二本卷总分6 7 8 分数已知函数()log (2)1a f x x =+-，其中1a >.（Ⅰ）若()f x 在[0,1]上的最大值与最小值互为相反数，求a 的值； （Ⅱ）若()f x 的图象不经过第二象限，求a 的取值范围.7.（本小题满分10分）已知函数()|2|f x x x =-. （Ⅰ）解不等式()3f x <；（Ⅱ）设0a >，求()f x 在区间[0,]a 上的最大值.8.（本小题满分10分）设函数()f x ，()g x 的定义域分别为f g D D ，，且f g D D Ø.若对于任意f x D ∈，都有()()g x f x =，则称()g x 为()f x 在g D 上的一个延拓函数.给定2() 1 (01)f x x x =-<≤.（Ⅰ）若()h x 是()f x 在[1,1]-上的延拓函数，且()h x 为奇函数，求()h x 的解析式； （Ⅱ）设()g x 为()f x 在(0,)+∞上的任意一个延拓函数，且()g x y x=是(0,)+∞上的单调函数.（ⅰ）判断函数()g x y x=在(0,1]上的单调性，并加以证明； （ⅱ）设0s >，0t >，证明：()()()g s t g s g t +>+.北京市西城区2013 —2014学年度第一学期期末试卷高一数学参考答案及评分标准2014.1A卷[必修模块4] 满分100分一、选择题：本大题共10小题，每小题4分，共40分.1.D；2.D；3.C；4.B；5.C；6.A；7.A；8.B；9.C；10.D.二、填空题：本大题共6小题，每小题4分，共24分.11.12-；12.3π，或32π；13.6-；14.55-；15.12；16.sin3x等（答案不唯一）.注：12题，得出一个正确的结论得2分.三、解答题：本大题共3小题，共36分.17.（本小题满分12分）（Ⅰ）解：因为3 tan4=-α，所以πtan tanπ4tan()π41tan tan4--=+⋅ααα【3分】7=-. 【6分】（Ⅱ）解：因为3 tan4=-α，所以2sin 3cos 2tan 33sin 2cos 3tan 2--=--αααααα 【 9分】 1817=. 【12分】18.（本小题满分12分） （Ⅰ）解：1cos 4()3sin 2cos 22xf x x x -=+⋅ 1cos 43sin 422x x -=+ 【 2分】 1sin(4)62x π=-+． 【 4分】因为 242T ππ==，所以()f x 的最小正周期是2π． 【 6分】（Ⅱ）解：由（Ⅰ）得，1()sin(4)62f x x π=-+．因为 84x ππ≤≤，所以 54366x πππ≤-≤， 【 8分】所以 1sin(4)126x π≤-≤， 【 9分】所以 131sin(4)622x π≤-+≤． 【10分】所以，当6x π=时，()f x 取得最大值32；当4x π=时，()f x 取得最小值1．【12分】19.（本小题满分12分）（Ⅰ）解：如图，以AB 所在直线为x 轴，以A 为坐标原点建立平面直角坐标系. 【 1分】因为ABCDEF 是边长为1的正六边形，且,M N 分别是,BC DE 的中点，所以 53(,)44M ，1(,3)2N ， 【 3分】 所以 5311848AM AN ⋅=+=. 【 4分】 （Ⅱ）解：设BM DN t ==，则[0,1]t ∈.【 5分】所以3(1,)22t M t +，(1,3)N t -. 【 7分】 所以3(1)(1)22t AM AN t t ⋅=+⋅-+2112t t ++=-213(1)22t =--+ 【10分】当0t =时，AM AN ⋅取得最小值1； 【11分】 当1t =时，AM AN ⋅取得最大值32. 【12分】B 卷 [学期综合] 满分50分一、填空题：本大题共5小题，每小题4分，共20分.1.{|01}x x <<；2.c b a <<；3. [1,)+∞；4. 2；5.②④. 注：5题，选出一个正确的序号得2分，有错选不给分. 二、解答题：本大题共3小题，共30分.6.（本小题满分10分）（Ⅰ）解：函数()log (2)1a f x x =+-的定义域是(2,)-+∞. 【 1分】因为 1a >，所以 ()log (2)1a f x x =+-是[0,1]上的增函数. 【 2分】 所以 ()f x 在[0,1]上的最大值是(1)log 31a f =-；最小值是(0)log 21a f =-. 【 4分】 依题意，得 log 31(log 21)a a -=--， 【 5分】 解得 6a =. 【 6分】（Ⅱ）解：由（Ⅰ）知，()log (2)1a f x x =+-是(2,)-+∞上的增函数. 【 7分】在()f x 的解析式中，令0x =，得(0)log 21a f =-， 所以，()f x 的图象与y 轴交于点(0,log 21)a -. 【 8分】依题意，得(0)log 210a f =-≤， 【 9分】 解得 2a ≥. 【10分】7.（本小题满分10分）（Ⅰ）解：原不等式可化为22230x x x ≥⎧⎨--<⎩，， （1） 或22230.x x x <⎧⎨-+>⎩，（2） 【 1分】解不等式组（1），得 23x ≤<；解不等式组（2），得2x <. 【 3分】 所以原不等式的解集为{|3}x x <. 【 4分】（Ⅱ）解：222,2,()|2|2, 2.x x x f x x x x x x ⎧-≥⎪=-=⎨-+<⎪⎩ 【 5分】① 当01a <<时，()f x 是[0,]a 上的增函数，此时()f x 在[0,]a 上的最大值是2()2f a a a =-+. 【 6分】 ② 当12a ≤≤时，()f x 在[0,1]上是增函数，在[1,]a 上是减函数，此时()f x 在[0,]a 上的最大值是(1)1f =. 【 7分】③ 当2a >时，令()(1)(2)10f a f a a -=-->， 解得12a >+. 所以，当212a <≤+时，此时()(1)f a f ≤，()f x 在[0,]a 上的最大值是(1)1f =； 当12a >+时，此时()(1)f a f >，()f x 在[0,]a 上的最大值是2()2f a a a =-.【 9分】 记()f x 在区间[0,]a 上的最大值为()g a ，所以 222,01,()1,112,2,1 2.a a a g a a a a a ⎧-+<<⎪⎪=≤≤+⎨⎪->+⎪⎩ 【10分】8.（本小题满分10分）（Ⅰ）解：当0x =时，由()h x 为奇函数，得(0)0h =. 【 1分】任取[10)x ∈-，，则(01]x -∈，， 由()h x 为奇函数，得22()()[()1]1h x h x x x =--=---=-+， 【 2分】所以()h x 的解析式为221,01,()0,0,1,10.x x h x x x x ⎧-<≤⎪==⎨⎪-+-≤<⎩【 3分】（Ⅱ）解：（ⅰ）函数()g x y x=是(0,1]上的增函数. 【 4分】 证明如下：因为()g x 为()f x 在(0,)+∞上的一个延拓函数， 所以当(01]x ∈，时，2()()1g x f x x ==-. 记()()1()g x f x k x x x x x===-，其中(0,1]x ∈. 任取12,(0,1]x x ∈，且12x x <，则210x x x ∆=->， 因为211221212112()(1)11()()()0x x x x y k x k x x x x x x x -+∆=-=---=>， 所以函数()g x y x=是(0,1]上的增函数. 【 6分】 （ⅱ）由()g x y x = 是(0,)+∞上的单调函数，且(0,1]x ∈时，()g x y x =是增函数，从而得到函数()g x y x= 是(0,)+∞上的增函数. 【 7分】因为 0s >，0t >， 所以 s t s +>，s t t +>， 所以()()g s t g s s t s+>+， 即 ()()()s g s t s t g s ⋅+>+⋅. 【 8分】 同理可得：()()()t g s t s t g t ⋅+>+⋅.将上述两个不等式相加，并除以s t +，即得 ()()()g s t g s g t +>+. 【10分】。

7.22014年高一数学必修4考试题（6）说明：本试卷分第I 卷（选择题）和第n 卷（非选择题）两部分 案写在答题卷（卡）上，交卷时只交答题卷（卡）.第I 卷（选择题，共36 分）A)3A. sin 11° ：：cos10° ：：sin168°B. sin 11° ：：s in 168° ：：cos10°1. 、选择题（本大题共 12小题，每小题 tan 300的值为（3分，共36分）.2. UlID uuu已知 AB =(4,1), BC =(_1,k)，若 A , B ，C 三点共线，则实数 k 的值为（3. C. -14 ir ur 已知两个单位向量 e 的夹角为日，则下列结论 不正确的是 A. 4 B. -4 D .-44. 5. 6.C . ur ur e 在e 2方向上的投影为cose ur uuB . e ◎ =1 ur 2 8 1«2 e 2 ir ur ur uu D . G e2)— G -q) E , F 分别是△ ABC 的边AB , BC, CA 的中点，则（UU uuu uu r A . AD BECF =0uir uuirunrB . BD-CF DF =0 uuir uuuuuuC . ADCE -CF =0uuu uuu urn r D. BD -BE -FC =0 已知 D , 已知扇形的圆心角的弧度数为 A. 2 B.4 2,扇形的弧长为 4,则扇形的面积为（C. 8D.16F 列关系式中正确的是（ .满分100分，考试时间100分钟.答C.、、3D.弋；3C. sin168o:: sin11o：：cos10oD. sin 168o：：cos10o：： sin11o已知sin（30°匕）-，则cos（60o Y）的值为（7.2B. -12=2,c = a b,且c_a ，则向量a 与b 的夹角为(二、填空题(本大题共 4小题，每小题4分，共16分)13. 函数y =山-tanx 的定义域是 _________________________________ .214. 函数 y =sin x+cosx 的值域是 _____________________________ . 15. 下面四个命题中， 其中正确命题的序号为 ______________ .① 函数f (x) = tanx 是周期为兀的偶函数；② 若：•、1是第一象限的角，且：；a ，则sin 〉- sin 1 ; 兀5 ③ x 是函数y =sin(2x)的一条对称轴方程；84④ 在(，)内方程tan x =sinx 有3个解.2 2uur uuu16. 在厶 ABC 中，AB = 4，AC= 3，也A =60。

2014-2015年高一数学必修五试题一、选择题（本大题共10小题，每小题5分，共50分）.1．已知集合2{(1)37,},A x x x x R =-<+∈0,1x B x x ⎧⎫=≤⎨⎬+⎩⎭则A B ⋂= ( )A ．[]1,0-B ．()1,0-C ．(]1,0-D ．[)1,0-2．在ABC ∆中，若2,60a b B ︒===，则此三角形（ )A ．无解B ．有一解C ．有两解D ．解的个数无法确定 3．在数列{}n a 中，1121,,2nn n a a a a +==+则该数列的第5项为（ ） A ．12 B ．25 C ．13 D ．23 4．如图所示，表示阴影部分的二元一次不等式组是（ ）A ．202400x y x y x --<⎧⎪+->⎨⎪≥⎩B ．20240x y x y x --<⎧⎪+-<⎨⎪≥⎩C ．202400x y x y x -->⎧⎪+-<⎨⎪≥⎩D ．202400x y x y x -->⎧⎪+->⎨⎪≥⎩5．等比数列{}n a 的前项和为n S ，已知123,2,3S S S A ．3-B ．13-C ．3D ．136．设01b a <<<，则下列不等式不成立的是（ ）A ．222ba<< B ．11220log log a b << C ．21ab b << D ．21ab a <<7．在ABC ∆中，角A 、B 、C 所对的边分别为a b c 、、，若角3C π>，sin 2sin a C b A =，则下列结论正确的有 （ ）个①一定是锐角三角形；②一定是等腰三角形；③可能是等腰直角三角形；④可能是等边三角形 A ．1 B ．2 C ．3 D ．48．已知等差数列{}n a ，{}n b 的前n 项和分别为,n n S T ，且9593n n S n T n +=+，则使得n na b 为整数的正整数的个数是（ ）A ．5B ．4C ．3D ．29．若数列{}n a 满足：132a =，112(2,3,4,)221n n a n a -=-=+，且有一个形如sin()n a A n ωϕ=+的通项公式，其中,,A ωϕ均为实数，且0ω>，则此通项公式n a 可以为（ ）A ．32sin 236n a n ππ⎛⎫=- ⎪⎝⎭B ．2233n a n ππ⎛⎫=+ ⎪⎝⎭C ．325sin 236n a n ππ⎛⎫=-+ ⎪⎝⎭D ．233n a n ππ⎛⎫=- ⎪⎝⎭10．定义在R 上的函数()y f x =是减函数，且对任意的a R ∈，都有()()0f a f a -+=，若x y 、满足不等式22(2)(2)0f x x f y y -+-≤，则当14x ≤≤时，2x y -的最小值为（ ）A ．4-B ．1-C ．0D ．8二、填空题（本大题共5小题，每小题5分，共25分） 11．《莱因徳纸草书》是世界上最古老的数学著作之一。

高中数学必修四和必修五综合测试题本卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟。

第Ⅰ卷注意事项：1．请将第Ⅰ卷的答案涂写在答题卡上；2．本卷共12小题，每题5分，共60分。

在每个小题给出的四个选项中，只有一项是符合题目要求的；3．交卷时，只交答题纸。

一、选择题（每题5分，共60分）1、设0a b <<，则下列不等式中正确的是（）A.2a ba b ab +<<<B ．2a b a ab b +<<< C ．2a b a ab b +<<< D ．2a b ab a b +<<<2、已知等比数列{}n a 的公比2=q ，前n 项和为n S ，则42S a =（） A.2 B.4 C.152D.1723、已知不等式02>++c bx ax 的解集为()3,2，则02>++a bx cx 的解集为 A.⎪⎭⎫⎝⎛21,31 B.⎪⎭⎫ ⎝⎛∞31-，∪⎪⎭⎫ ⎝⎛∞+，21 C.⎪⎭⎫ ⎝⎛31,-21- D.⎪⎭⎫ ⎝⎛∞21--，∪⎪⎭⎫⎝⎛∞+，31-4、已知函数()42322+++=kx kx x x f 的定义域是R ，则k 的取值范围是（）A.()4,0B.[)4,0C.(]4,0D.[]4,05、已知21,x x 是关于x 的一元二次方程()032=+++a ax x 的两实根，则2221x x +的最小值为（）A.7-B.0C.2D.18 6、下列命题正确的是（）A ．22bc ac b a >⇒>B ．320b b a b a >⇒<<C ．01>>⇒>b b a b a 且D ．ba ab b a 110,33<⇒>>7、设n S 为等差数列{}n a 的前n 项和，若11a =，公差2d =，362=-+k k S S ，则k =（）A ．8B ．7C ．6D ．58、已知{}n a 为等比数列，472a a +=，568a a =-，则110a a +=（）A.7B.5C.-5D.-79、已知()x f y =是开口向上的二次函数，且()()x f x f -11=+恒成立.若()()2-31x f x f <+，则x 的取值范围是（） A.⎪⎭⎫⎝⎛2343， B.⎪⎭⎫ ⎝⎛∞43-，∪⎪⎭⎫ ⎝⎛∞+，23 C.⎪⎭⎫ ⎝⎛43-23-， D.⎪⎭⎫ ⎝⎛∞23--，∪⎪⎭⎫ ⎝⎛∞+，43- 10、已知C B A 、、三点共线()在该直线外O ，数列{}n a 是等差数列，n S 是数列{}n a 的前n 项和.若OC OB OA 20121⋅+⋅=a a ，则=2012S （） A.1006B.2012C.1005D.201011、已知⎥⎦⎤⎝⎛∈20πθ，，则函数()θθθsin 2sin +=f 的最小值为（）A ．22 B.3C.32 D.212、定义在R 上的偶函数()x f 满足()()x f x f =+2，且在[]2,-3-上是减函数.若B A 、是锐角三角形的两内角，则有（） A.()()B cos A sin f f > B.()()sinB A sin f f > C.()()B cos A sin f f < D.()()B cos A cos f f >第Ⅱ卷二、填空题（共4个小题，每小题5分，共20分；把答案填答题纸上）13、在AB C ∆中，3B π=中，且34BC BA =⋅,则AB C ∆的面积是________.14、设,x y 满足约束条件：⎪⎪⎩⎪⎪⎨⎧≥≥≤+≥.0,0,3,1--y x y x y x 则2z x y =-的取值范围为. 15、已知0,0x y >>，若2282y x m m x y+>+恒成立，则实数m 的取值范围是. 16、已知y b a x y x ,,,,0,0>>成等差数列，y d c x ,,,成等比数列，则()cdb a 2+的最小值是.三、解答题（共6小题，17题10分，18—22题各12分，共70分；解答应写出文字说明，证明过程或演算步骤）17、已知数列{}n a 中，11=a ，321+=+n n a a ，求数列{}n a 通项公式n a .18、已知a 千克的糖水中含有b 千克的糖；若再加入m 千克的糖()0,0>>>m b a ，则糖水变甜了.请你根据这个事实，写出一个不等式；并证明不等式ma mb ab ++<()0,0>>>m b a 成立，请写出证明的详细过程.19、已知ABC ∆的角A B C 、、所对的边分别是a b c 、、，设向量(,),m a b =(sin ,cos ),n A B =(1)若//,m n 求角B 的大小;(2)若4=⋅p m,边长2=c ，角3C π=，求AB C ∆的面积.20、某种汽车的购车费用是10万元，每年使用的保险费、养路费、汽油费共约为0.9万元，年维修费用第一年是0.2万元，第二年是0.4万元，第三年是0.6万元，…，以后逐年递增0.2万元.汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用()x x N *∈年的维修费用总和为()g x ，年平均．．．费用为()f x . （1）求出函数()g x ，()f x 的解析式；（2）这种汽车使用多少年时，它的年平均费用最小？最小值是多少？ 21、设关于x 的函数()12-cos 2-cos 22+=a x a x y 的最小值为()a f .⑴试用a 写出()a f 的表达式；⑵试确定()21=a f 的a 的值，并对此时的a 求出y 的最大值. 22、在数列{}n a 中，已知1-1=a ，且()*+∈+=N 4-321n n a a n n .⑴求证：数列{}3-1++n n a a 是等比数列； ⑵求数列{}n a 的通项公式n a ；⑶求和：()*∈++++=N n a a a a S n n 321. 高一数学期末参考答案 一、选择题1-5BCABC6-10DADBA11-12BA 二、填空题13、614、[]33-，15、()24-，16、4 三、解答题（答题方法不唯一）17、由题知：()3231+=++n n a a ,···························4分 令3+=n n a b ，则4311=+=a b ，有21=+nn b b ,···························6分 11-224+=⋅=∴n n n b ,·····························8分即3-21+=n n a .·····························10分18、填空：ma mb ab ++<;··························4分证明：作()()()m a a b a m m a a bm ab am ab ab m a m b +-=++=++---, (6)分0-0>∴>>b a b a ,··························6分 又0>m 0->++∴ab m a m b ,··························8分即ma mb ab ++<.··························10分19、⑴n m∥bsinA B cos =∴a ,··························2分在AB C ∆中，由正弦定理得：B sin A sin a b =, (4)分B sin B cos a a =∴即1tanB =4B π=∴.··························6分⑵4=⋅p m 4=+∴b a ,··························8分又3C 2π==，c 由余弦定理C cos 2-222ab b a c +=得ab 3-442=,解得4=ab ,··························10分3232C sin 21S ABC =⨯==∴∆ab .··························12分 20、（1）由题意知使用x 年的维修总费用为()g x =()20.20.20.10.12x x x x +=+万元··························3分依题得2211[100.9(0.10.1)]((10.1))0f x x x x x x xx=+++=++····················6分（2）()f x 101012131010x x x x =++≥⋅+=·························8分当且仅当1010x x =即10x =时取等号··························10分10x ∴=时y 取得最小值3万元答：这种汽车使用10年时，它的年平均费用最小，最小值是3万元.··········12分21、⑴令[]1,1-,cos ∈=t t x ，则原式1-2-2-2-21-2-2-2222a a a t a at t ⎪⎭⎫ ⎝⎛== ①当()1-122，∈a 时，()1-2-2-2a a a f =；②当[)∞+∈，122a 时，()14-+=a a f ； ③当(]1,--22∞∈a时，()1=a f ；综上：()()[)(]⎪⎪⎪⎩⎪⎪⎪⎨⎧∞∈+∞∈+∈=.1,--2,1,,12,14-,1,1-2,1-2-2-2222a a a a a a a f⑵当()21=a f 时，解得1-=a ，当1-=a 时()1,1-,2121212222∈+⎪⎭⎫ ⎝⎛+=++=t t t t y 5=∴maz y 22、⑴令3-1+=+n n na ab ，则21=⇒+nn b b ∴数列{}n b 是为公比为2的等比数列. ⑵3-1-212==a a ,1-112123-13-n n n n a a b a a b =+=⇒=+=+, 1-23-4-32n n n a n a =++∴, ()*∈+=∴N 13-21-n n a n n .⑶设数列{}n a 的前n 项和为n T ,()()213-1-222-33-1-2T +=+=n n n n n n n , nn a a a +++= 21S .0,4,0,4>><≤n n a n a n ,4≤∴n 时，()n n n n n 2-2131-T S ++==,4>n 时，()213-2122T -T S 4++==n n n n n .。

2014-2015人教版高中数学必修四测试卷一、选择题1.下列命题正确的是（ ）C.终边相同的角一定相等D.不相等的角，它们终边必不相同12sin()24y x π=-+的周期，振幅，初相分别是（ ）A.4π，2，4πB.4π，2-，4π-C.4π，2，4πD.2π，2，4π1cos()2A π+=-，那么sin()2A π+=（ ）A.12B.12C.12D.122005sin(2004)2y x π=-是（ ）（1）零向量的长度为零，方向是任意的. （2）若a ，b 都是单位向量，则a ＝b . （3）向量AB 与向量BA 相等.（4）若非零向量AB 与CD 是共线向量，则A ，B ，C ，D 四点共线. 以上命题中，正确命题序号是（ ）A.（1）B.（2）C.（1）和（3）D.（1）和（4）(sin 2P θ，cos 2)θ位于第三象限，那么角θ所在象限是（ ）ABCD 中，如果0AB CD =，AB DC =，那么四边形ABCD α是第一象限角，则sin cos αα+的值与1的大小关系是（ ）A.sin cos 1αα+>B.sin cos 1αα+=C.sin cos 1αα+<△ABC 中，若sin 2cos sin C A B =，则此三角形必是（ ）A.等腰三角形B.正三角形C.直角三角形D.等腰直角三角形 10.如图，在△ABC 中，AD 、BE 、CF 分别是BC 、点G ，则下列各等式中不正确的是（ ） A.23BG BE =B.2CG GF =C.12DG AG =D.121332DA FC BC +=二、填空题（本大题共4小题，每小题5分，共20分）-3008cm ，面积为24cm ，则扇形的圆心角的弧度数是.tan 2α=，3tan()5αβ-=-，则tan β=.(3a =，1)，(sin b α=，cos )α，且a ∥b ，则4sin 2cos 5cos 3sin αααα-+＝.14.给出命题：（1）在平行四边形ABCD 中，AB AD AC +=.（2）在△ABC 中，若0AB AC <，则△ABC 是钝角三角形. （3）在空间四边形ABCD 中，,E F 分别是,BC DA 的中点，则1()2FE AB DC =+. 以上命题中，正确的命题序号是.三、解答题（本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤） 15.（本小题满分13分）已知3sin 25α=，53[,]42αππ∈. （1）求cos2α及cos α的值；（2）求满足条件sin()sin()2cos x x ααα--++=的锐角x . 16.（本小题满分13分） 已知函数()sin22x xf x =+，x R ∈. （1）求函数()f x 的最小正周期，并求函数()f x 在[2,2]x ππ∈-上的单调递增区间； （2）函数()sin ()f x x x R =∈的图象经过怎样的平移和伸缩变换可以得到函数()f x 的图象. 17.（本小题满分13分）已知电流I 与时间t 的关系式为sin()I A t ωϕ=+. （1）下图是sin()I A t ωϕ=+(0,)πωϕ>sin()I A t ωϕ=+的解析式；（2）如果t 在任意一段1150sin()I A t ωϕ=+都能取得最大值和最小值， 那么ω的最小正整数值是多少？ 18.（本小题满分13分）已知向量(3,4)OA =-，(6,3)OB =-，(5OC =- （1）若点,,A B C 能够成三角形，求实数m 应满足的条件；（2）若△ABC 为直角三角形，且A ∠为直角，求实数m 的值. 19.（本小题满分13分）设平面内的向量(1,7)OA =，(5,1)OB =，(2,1)OM =，点P 是直线OM 上的一个 动点，且8PA PB =-，求OP 的坐标及APB ∠的余弦值. 20.（本小题满分13分） 已知向量33(cos,sin )22x x a =，(cos ,sin )22x x b =-，且[,]2x ππ∈.（1）求a b 及a b +；（2）求函数()f x a b a b =++的最大值，并求使函数取得最大值时x 的值.高中数学必修（4）试卷参考答案及评分标准一、选择题二、填空题11. 2 12. -13 13. 5714. （1）（2）（3） 三、解答题15.解：（1）因为5342παπ<<，所以5232παπ<<. ………………………（2分） 因此4cos 25α==-. ………………………………（4分）由2cos 22cos 1αα=-，得cos 10α=-. ……………………（8分） （2）因为sin()sin()2cos x x ααα--++=， 所以2cos (1sin )x α-=1sin 2x =. ………………………（11分） 因为x 为锐角，所以6x π=. ………………………………………………（13分）16.解：sin2sin()2223x x x y π==+. （1）最小正周期2412T ππ==. ……………………………………………（3分）令123z x π=+，函数sin y z =单调递增区间是[2,2]()22k k k Z ππππ-++∈.由 1222232k x k πππππ-+≤+≤+， 得 544,33k x k k Z ππππ-+≤≤+∈. ………………………………（5分）取0k =，得533x ππ-≤≤，而5[,]33ππ-⊂[2,2]ππ-，所以，函数sin 22x x y =+，[2,2]x ππ∈-得单调递增区间是5[,]33ππ-.…………………………………………………………………………（8分） （2）把函数sin y x =图象向左平移3π，得到函数sin()3y x π=+的图象，…（10分） 再把函数sin()3y x π=+的图象上每个点的横坐标变为原来的2倍，纵坐标不变，得到函数sin()23x y π=+的图象， …………………………………（11分） 然后再把每个点的纵坐标变为原来的2倍，横坐标不变，即可得到函数2sin()23x y π=+的图象. …………………………………………………（13分）17.解：（1）由图可知300A =，设11900t =-，21180t =， ……………………（2分）则周期211112()2()18090075T t t =-=+=， …………………………（4分） ∴2150T πωπ==. ………………………………………………………（6分）1900t =-时，0I =，即1sin[150()]0900πϕ⋅-+=，sin()06πϕ-=. 而2πϕ<， ∴6πϕ=.故所求的解析式为300sin(150)6I t ππ=+. ……………………………（8分）（2）依题意，周期1150T ≤，即21150πω≤，(0)ω>， …………………（10分） ∴300942ωπ≥>，又*N ω∈，故最小正整数943ω=. ……………（13分） 18.解：（1）已知向量(3,4)OA =-，(6,3)OB =-，(5,3)OC m m =---，若点,,A B C 能构成三角形，则这三点不共线，即AB 与BC 不共线. ……（4分）(3,1)AB =，(2,1)AC m m =--，故知3(1)2m m -≠-， ∴实数12m ≠时，满足条件. …………………………………………………（8分） （若根据点,,A B C 能构成三角形，必须任意两边长的和大于第三边的长，即由ABBC CA +>去解答，相应给分）（2）若△ABC 为直角三角形，且A ∠为直角，则AB AC ⊥， …………（10分） ∴3(2)(1)0m m -+-=， 解得74m =. …………………………………………………………………（13分） 19.解：设(,)OP x y =. ∵点P 在直线OM 上，∴OP 与OM 共线，而OM (2,1)=，∴20x y -=，即2x y =，有(2,)OP y y =. ………………………………（2分） ∵(12,7)PA OA OP y y =-=--，(52,1)PB OB OP y y =-=--，……（4分） ∴(12)(52)(7)(1)PA PB y y y y =--+--，即252012PA PB y y =-+. …………………………………………………（6分）又8PA PB =-， ∴2520128y y -+=-，所以2y =，4x =，此时(4,2)OP =. ……………………………………（8分）(3,5),(1,1)PA PB =-=-.于是34,2,8PA PB PA PB ===-. …………………………………（10分）∴cos 34PA PB APB PA PB∠===⋅. ………………………（13分）20.解：（1）33coscos sin sin cos 22222x x x xa b x =-=， ……………………（3分） (cosa b +=………………………（4分）2cos x ==…………………………………………（7分）∵[,]2x ππ∈， ∴cos 0x <.∴2cos a b x +=-. …………………………………………………………（9分） （2）2()cos 22cos 2cos 2cos 1f x a b a b x x x x =++=-=--2132(cos )22x =--…………………………………………………（11分）∵[,]2x ππ∈， ∴1cos 0x -≤≤， ……………………………………（13分）∴当cos 1x =-，即x π=时max ()3f x =. ………………………………（15分）。

2014年数学必修4、必修5考试题(7)考试时间：120分钟 满分：150分一、选择题：本大题共10小题，每小题5分，满分50分在每小题给出的四个选项中，只有一项是符合题目要求的．[1．在等差数列{}n a 中，已知1232,13,a a a =+=则456a a a ++等于（ ） A ．40 B ．42 C ．43 D ．452．已知向量(12)a = ，，(4)b x = ，，若向量a b ∥，则x =（ ）A ．21-B ．21C ．2-D ．23．函数sin 22y x π⎛⎫=+⎪⎝⎭是（ ） A. 周期为π2的偶函数 B. 周期为π2的奇函数 C. 周期为π的偶函数 D. 周期为π的奇函数4．在△ABC 中，若a = 2 ,b =030A = , 则B 等于 （ ）A ．60B ．60 或 120C ．30D ．30 或1505．等差数列{a n }前9项的和等于前4项的和．若a 1＝1，a k ＋a 4＝0，则k ＝（ ）A ．10B ．9C ．8D ．76．已知函数()sin 2tan 1,(3)5,(3)f x a x b x f f π=++-=+=且则（ ） A ．3 B ．1 C ．－1 D ．－37．在等比数列{a n }中，若a 1＝12，a 4＝－4，则|a 1|＋|a 2|＋…＋|a n |＝（ ）A ．1122n -- B ．322n - C ． 1142n -- D ． 342n - 8．设｛a n ｝是由正数组成的等比数列，且a 5a 6=81，log 3a 1+ log 3a 2+…+ log 3a 10的值是（ ）A ．5B ．10；C ．20D ．2或49．设{}n a 是首项为1的正项数列，且()011221=+-+++n n n n a a na a n (n =1，2，3，…)，则它的通项公式是100a =( ). A ．100 B ．1100C ．101D ．110110．若函数22()(sin cos )2cos f x x x x m =++-在0,2π⎡⎤⎢⎥⎣⎦上有零点，则m 的取值范围为（ ）A. []1,2-B. []1,3C. 1,2⎡-+⎣D. 1,2⎡+⎣二、填空题：本大题共4小题， 每小题5分，满分20分．11．设｛a n ｝是公比为q 的等比数列，S n 是它的前n 项和．若｛S n ｝是等差数列，则q =12．已知向量()1,1=a ，()2,n =b ，若+=a b a b ，则n = .13．在 ABC ∆中，内角A 、B 、C 依次成等差数列，8,5AB BC ==， 则ABC ∆外接圆的面积为__ ___.14. 两千多年前，古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题，他们在沙滩上画点或用小石子来表示数，按照点或小石子能排列的形状对数进行分类，如图1中的实心点个数1，5，12，22，…，被称为五角形数，其中第1个五角形数记作11a =，第2个五角形数记作25a =，第3个五角形数记作312a =，第4个五角形数记作422a =，……，若按此规律继续下去，则5a = ，若145n a =，则n = ．三、解答题：本大题共6小题，满分80分。

2014年高一数学必修3、必修4考试题(9)DA．1 B．12 C．22D．3二、填空题（本大题共4小题，每小题5分，共20分）11．A，B，C三种零件，其中B零件300个，C 零件200个，采用分层抽样方法抽取一个容量为45的样本，A零件被抽取20个，C零件被抽取10个，三种零件总共有___ _个。

12．计算sin43cos13sin13cos43的值等于_____ __.13. 已知x、y的取值如下表所示：x 0 1 3 4y 2.2 4.3 4.8 6.7从散点图分析，y 与x 线性相关，且ˆˆ0.95yx a =+，则ˆa =． 14. _______________)32tan(的定义域是函数π-=x y三、解答题（本大题共6小题，共75分）15．（本题12分）求值 2sin840cos540tan 225cos(330)sin(210)++--+-16．（本题13分） “你低碳了吗？”这是某市为倡导建设节约型社会而发布的公益广告里的一句话．活动组织者为了了解这则广告的宣传效果，随机抽取了120名年龄在[10，20) ，[20，30) ，…， [50，60) 的市民进行问卷调查，由此得到的样本的频率分布直方图如图所示．(1) 根据直方图填写右面频率分布统计表； (2) 根据直方图，试估计受访市民年龄的中位数0.050.20.1563018[40,50)[30,40)[50,60)[20,30)[10,20)频率频数分组（保留整数）；(3) 按分层抽样的方法在受访市民中抽取n名市民作为本次活动的获奖者，若在[10，20)的年龄组中随机抽取了6人，则的n值为多少？17．（本题12分）在人流量较大的街道，有一中年人吆喝“送钱”，只见他手拿一黑色小布袋，袋中有3只黄色、3只白色的乒乓球（其体积、质地完成相同），旁边立着一块小黑板写道：摸球方法：从袋中随机摸出3个球，若摸得同一颜色的3个球，摊主送给摸球者5元钱；若摸得非同一颜色的3个球，摸球者付给摊主1元钱。

2014年高一数学必修4考试题（2）本试卷分选择题和非选择题两部分，共3页，满分150分．考试时间100分钟． 注意事项：1. 答第一部分（选择题）之前，务必将自己的姓名、座位号、考试科目用铅笔涂写在答题卡上．2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡．．．．．．．．．．．．．．．．．．．．．．．．．．．皮擦干净后，再选涂其他答案，不能答在试题卷上．．．．．．．．．．．．．．．．．．．．．．．．3. 考试结束后，监考人将答题卡收回，试卷考生自己保管．第一部分（选择题，每小题5分，共50分）1、角α终边过点(1,2)-，则cos α＝（ ）A 、55 B 、255 C 、55- D 、255- 2、如图所示，D 是ABC ∆的边AB 上的中点，则向量CD =（ ）（A ）12BC BA -+ （B ） 12BC BA --(C). 12BC BA - (D). 12BC BA +3、已知向量(2,3)a = ，(1,2)b =-，若4ma b + 与b a 2-共线，则m 的值为A21 B 2 C 21- D 2- 4、已知点P （3，2）与点Q （1，4）关于直线l 对称，则直线l 的方程为 （ ） A ．01=+-y x B ．0=-y xC ．01=++y xD ．0=+y x 5、已知α∈(2π,π)，sin α=53,则tan(4πα+)等于（ ） A ．71 B ．7 C ．－ 71D ．－76、24cos cos y x x =-的最小正周期是（ ）A ．2π B ． π C ．32π D ．2π 7、圆074422=+--+y x y x 上的动点P 到直线0=+y x 的最小距离为 A ．1 B ． 122- C ． 2 D ． 22ADCB8、在函数52sin(4)23y x π=-+的图象与x 轴的各个交点中，离原点最近的一点（ ） A ．,06π⎛⎫- ⎪⎝⎭ B ．,012π⎛⎫- ⎪⎝⎭ C ．,012π⎛⎫ ⎪⎝⎭ D ．,06π⎛⎫ ⎪⎝⎭9、已知向量()()cos ,sin ,cos ,sin a b ααββ==,且αβ≠则a 与b 一定满足A 、a 与b 的夹角等于αβ-B 、a b ⊥C 、//a bD 、()a b + ()a b ⊥-10、 定义在R 上的偶函数()f x 满足()()2f x f x =+，当[]3,4x ∈时，()2f x x =-，则 （ ） A ．11sincos 22f f ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭B ．()()sin1cos1f f <C ．sin cos 33f f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭D ．33sin cos 22f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭第二部分（非选择题，共100分）二、填空题：本大题共有4个小题，每小题5分，共20分。