箱梁截面有效宽度计算

梁配筋计算梁截面、材料信息梁宽度b= 250 mm梁高度h= 600 mmas= 60 mm a's= 35 mmh0= 540 mm梁自重 3.75 kN/m混凝土选用 C 30fc= 14.3 N/㎜2 a1= 1ft= 1.43 N/㎜2 b1= 0.8钢筋选用 2 其中，1; HPB235级钢2; HRB335级钢3; HRB400级钢fy=f'y= 300 N/㎜2 ξb= 0.550A）单筋矩形截面在纵向受拉钢筋达到充分发挥作用或不出现超筋破坏所能承受的最大弯矩设计值Mu,max= 415.68 kNmB）单筋矩形截面已知弯矩求配筋M实际= 128 kNm845.69 ㎜2取钢筋直径￠＝ 18 实取 4 根实配钢筋面积AS= 1017.88 mm2 OK!Asmin= 322.5 < AsAsmax= 3539.7 > AsC）双筋矩形截面已知弯矩求配筋M实际= 243 kNm < Mu,max受压区砼和相应的一部分受力钢筋As1的拉力所承担的受弯承载力Mu1 Mu1=Mu,max= 415.68 kNm= 3539.25 ㎜2由受压钢筋及相应的受拉钢筋承受的弯矩设计值为Mu2=M-Mu1= -172.68 kNm因此所需的受压钢筋为-1139.83 ㎜2与其对应的那部分受拉钢筋截面面积为As2=A's= -1139.83 ㎜2纵向受拉钢筋总截面面积As＝As1＋As2= 2399.42 ㎜2受拉钢筋取钢筋直径￠＝ 20 实取 9 根实配钢筋面积AS= 2827.43 mm2 OK!受压钢筋取钢筋直径￠＝ 12 实取 2 根实配钢筋面积AS= 226.19 mm2 OK!验算受压区高度x＝fyAs1/(α1fcb)= 297.00 mm2α's＝ 70.00 mm ≤ x OK!D）双筋矩形截面已知弯矩和受压钢筋求受拉配筋M实际= 80 kNm > Mu,max已知： A's＝ 942.48 3 ￠ 20为充分发挥受压钢筋A's的作用，取As2=A's= 942.48 mm2Mu2=f'yA's(h0-a's)= 142.79 kNm由弯矩Mu1按单筋矩形截面求As1Mu1=M-Mu2= -62.79 kNm因此所需的受压钢筋为-376.55 ㎜2纵向受拉钢筋总截面面积As＝As1＋As2= 565.93 ㎜2受拉钢筋取钢筋直径￠＝ 20 实取 8 根实配钢筋面积AS= 2513.27 mm2 OK!验算受压区高度x＝fyAs1/(α1fcb)= -31.60 mm 2α's＝ 70 mm ＞ x NO。

箱梁截面有效宽度的理解和应用鲁金玉摘要本文从分析截面产生的剪力滞效应开始，阐述了考虑截面有效宽度的原因、介绍了“新桥规”对有效宽度的计算的妥善方法，以及使用中的使用场合、计算过程以及介绍了现行桥梁设计通用程序《桥梁博士》对截面有效宽度的考虑。

关键词剪力滞有效宽度桥规桥梁博士1、剪力滞与箱梁有效宽度T梁、箱梁、Π行等带肋梁结构在外力作用下产生弯曲内力和变形，通过梁肋的剪切变形传递给翼板。

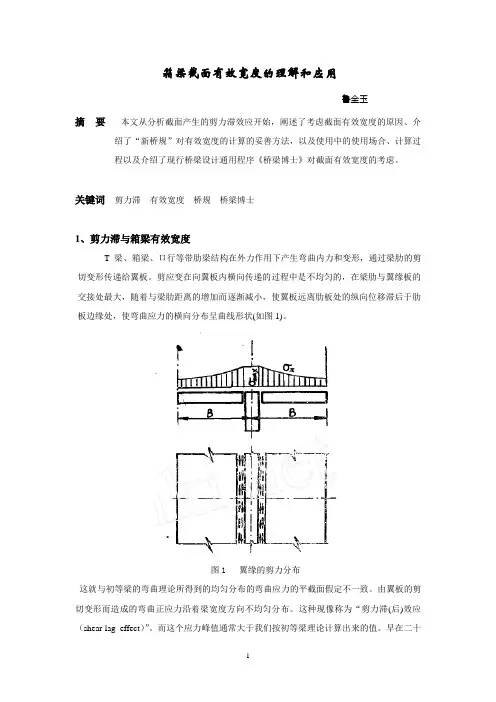
剪应变在向翼板内横向传递的过程中是不均匀的，在梁肋与翼缘板的交接处最大，随着与梁肋距离的增加而逐渐减小，使翼板远离肋板处的纵向位移滞后于肋板边缘处，使弯曲应力的横向分布呈曲线形状(如图1)。

图1 翼缘的剪力分布这就与初等梁的弯曲理论所得到的均匀分布的弯曲应力的平截面假定不一致。

由翼板的剪切变形而造成的弯曲正应力沿着梁宽度方向不均匀分布。

这种现像称为“剪力滞(后)效应（shear-lag effect）”。

而这个应力峰值通常大于我们按初等梁理论计算出来的值。

早在二十世纪初就有人进行这方面的研究，认为剪力滞后效应可能导致钢箱梁截面的严重破坏。

因此工程设计人员提出了“有效宽度”的概念，即将翼缘实际宽度按某个系数或者某种规律折减为计算宽度，使折减后的宽度按初等梁理论算得的应力值和实际的峰值接近，以确保结构的安全。

2、有效宽度的几何计算方法有效分布宽度问题, 实质上是以剪力滞理论为基础。

用精确的理论来分析翼缘应力的不均匀分布规律是比较复杂的, 尤其不便于工程中的应用。

为了既能利用简单的初等梁理论公式, 又能得到接近于翼缘实际应力的最大值, 便提出“翼缘有效宽度”的概念,并且由T.V.卡曼首先解决, 一直沿用至今。

翼缘有效宽度的简单定义是按初等梁理论的公式也能算得与真实应力峰值接近相等的那个翼缘折算宽度。

它的几何解释是：如图二中的真实应力峰值σmax为高度的阴影矩形面积等于真实的应力曲线所包围的面积，即阴影线矩形面积的边长，便是翼缘的有效宽度，数学表达式为：式中：be为每侧翼缘的有效宽度，b为每侧翼缘的净宽度，t为翼缘的厚度，σmax为腹板与翼板连接处的应力峰值，x为沿跨长方向的坐标，y为沿横截面宽度方向的坐标。

混凝土箱形截面计算公式引言。

混凝土箱形截面是工程结构中常见的一种截面形式，它具有较好的承载能力和抗震性能，被广泛应用于桥梁、建筑、水利工程等领域。

在设计和施工过程中，混凝土箱形截面的计算是至关重要的，它直接影响着结构的安全性和稳定性。

本文将介绍混凝土箱形截面的计算公式，帮助工程师和设计人员更好地理解和应用这些公式。

一、混凝土箱形截面的基本特点。

混凝土箱形截面是由上下板和四个侧板组成的矩形或近似矩形的截面形式，其特点包括：1. 承载能力强，混凝土箱形截面由于具有较大的截面面积和惯性矩，其承载能力较强，能够承受较大的荷载。

2. 抗震性能好，混凝土箱形截面由于具有较好的截面稳定性和刚度，其抗震性能较好，能够有效地减少结构的振动和变形。

3. 施工便利，混凝土箱形截面的施工工艺相对简单，能够通过模板一次性浇筑成型，施工效率较高。

二、混凝土箱形截面的计算公式。

混凝土箱形截面的计算公式主要包括截面面积、惯性矩、受压区高度等参数的计算。

具体公式如下：1. 截面面积的计算公式。

混凝土箱形截面的面积可以通过下面的公式进行计算：A = bh。

其中，A表示截面面积，b表示截面的宽度，h表示截面的高度。

2. 惯性矩的计算公式。

混凝土箱形截面的惯性矩可以通过下面的公式进行计算：I = (1/12)bh^3。

其中，I表示截面的惯性矩，b表示截面的宽度，h表示截面的高度。

3. 受压区高度的计算公式。

混凝土箱形截面的受压区高度可以通过下面的公式进行计算：h_c = h-0.5α。

其中，h_c表示受压区的高度，h表示截面的高度，α表示混凝土箱形截面的厚度。

以上公式是混凝土箱形截面常用的计算公式，通过这些公式可以快速准确地计算出混凝土箱形截面的各项参数，为工程设计和施工提供了重要的参考数据。

三、混凝土箱形截面的设计原则。

在进行混凝土箱形截面的设计时，需要遵循一些基本的设计原则，以确保结构的安全性和稳定性。

这些设计原则包括：1. 合理确定截面尺寸，混凝土箱形截面的尺寸应根据结构的受力情况和使用要求合理确定，以满足结构的承载和使用性能要求。

梁的截面尺寸计算通常涉及到多种参数，如荷载、材料特性、梁的长度等。

下面是一些常见的梁截面尺寸计算公式:
1.弯曲应力计算：
弯曲应力是梁截面上由于弯曲而引起的应力。

弯曲应力的计算公式为：σ= M * c / S
其中，
σ是弯曲应力（单位：Pa），
M 是梁上的弯矩（单位：Nm），
c 是梁截面上离中性轴最远点的距离（也称为最大截面偏心距，单位：m），
S 是梁截面的抵抗矩（单位：m^3）。

2.剪切应力计算：
剪切应力是梁截面上由于剪力而引起的应力。

剪切应力的计算公式为：τ= V * Q / (I * b)
其中，
τ是剪切应力（单位：Pa），
V 是梁上的剪力（单位：N），
Q 是梁截面的截面模量（单位：m^3），
I 是梁截面的惯性矩（单位：m^4），
b 是梁截面的宽度（单位：m）。

3.拉伸应力计算：
拉伸应力是梁截面上由于拉伸力而引起的应力。

拉伸应力的计算公式为：
σ= F / A
其中，
σ是拉伸应力（单位：Pa），
F 是梁上的拉伸力（单位：N），
A 是梁截面的面积（单位：m^2）。

此外，还需要考虑梁的材料特性，如弹性模量（E）和抗拉强度（σ_yield）。

这些参数用于验证梁的强度和稳定性。

对于具体的工程设计，还需要根据梁的加载情况、支承条件、设计要求等进行进一步的计算和分析。

通常会参考结构设计规范和使用专业的结构分析软件进行详细的截面尺寸计算。

二、支架设计承载力参数1、立杆设计荷载2、横杆设计荷载3、方木、模板设计参数[σw] = 13MPa[ τ] = 1.9 MPaE = 1.0×104 MPa10×10cm方木截面抵抗矩：A=bh=100*100=10000mm2I=bh3/12=100*1003/12=8.33*106mm4W=bh2/6=100*1002/6=1.67*105mm3S m=bh2/8=100*1002/8=1.25*105mm3三、箱梁砼自重参数箱梁具体尺寸见设计院图纸。

1、箱梁砼容重按25kN/m3，本次计算按箱梁腹板荷载计算，翼板因荷载偏小，不在验算范围内。

2、箱梁普通截面段腹板每延米砼恒载计算：腹板截面S=0.5*1.7=0.85m2，每延米砼恒载P1=0.85×25=21.25kN/m。

3、横梁、端梁每延米砼恒载计算：(按最不利荷载截面即纵向的横截面计算)箱梁截面S=16.75×1.7=28.475m2每延米砼恒载P2=28.475×25=711.875kN/m，中横梁宽为2m，端梁宽1.2m。

四、荷载组合1、人员及施工机械设备荷载P3=3.5kN/m22、混凝土倾倒及振捣产生的荷载P4=2kN/m2荷载组合按照Ⅱ类荷载组合计算，P＝1.2恒载+1.4活载五、支撑体系验算（一）箱梁普通截面段1、模板验算（1）底板模板验算：模板每延米荷载计算：q＝1.2*P1+1.4(P3+P4)*0.5=1.2*21.25+1.4(3.5+2)*0.5=29.35KN/m腹板宽度为500mm，板宽按0.5m计算。

1.计算简图箱梁模板底横向10×10cm方木间距均为300cm，按均布荷载作用下的二等跨连续梁计算。

2.截面特性A=bh=500*20=10000mm2I=bh3/12=500*203/12=333333mm4W=bh2/6=500*202/6=33333mm3S m=bh2/8=500*202/8=25000mm33.截面验算max＝0.096，剪力系数Kv B＝0.626+0.625＝1.25，扰查表可知：弯距系数Km中度系数Kw＝0.521中(1)抗弯强度验算M max=M中=0.096qL2=0.096*29.35*0.32=0.254kN·mσ=M max/W=0.254*106/33333=7.61Mpa<[σw]=13.0Mpa满足要求(2)剪切强度验算Q max=1.25qL=1.25*29.35*0.3=11.006kNτmax=QS m/I m b=11.006*103*25000/(333333*500)=1.65MPa< [τ]=1.9 MPa满足要求(3)挠度验算f max=0.521qL4/（100EI）=0.521*27.85*3004/(100*1.0*104*333333)=0.352mm< [ f ]=L/400=300/400=0.75mm满足要求（2）侧板模板验算：混凝土等级为C50，坍落度选用160～180mm，砼容重为γc＝25 KN/m3，采用汽车泵导管运送混凝土至箱梁，浇筑速度V＝2m/h，砼温度为30℃，用插入式振捣器振捣。

箱梁横梁计算请问大家：1）桥博计算连续梁的横隔梁时建模仅取横隔梁的宽度还是取横隔梁的两侧渐变段的截面作为模型计算截面？2）对于箱梁的恒载如何处理，是作为均布荷载加载在桥面板上，还是作为集中力加载在腹板上？3）对于顶板带横向预应力的桥梁，计算出来的结果是不是不考虑翼板根部的拉应力？4）对于多室截面恒载如何分担？希望大家发表自己的看法，如果有相关的算例最好上传学习一下!向别的老工程师请教后他给我这样的解释：不知道大家有什么见解1、横梁截面宽度取(b+2bh+12h'f)，b为横梁厚度，bh为承托长度，h'f为板厚。

2、箱梁恒载主要都由腹板传递，取集中力加在腹板上。

3、个人认为应当考虑，施加横向预应力主要就是解决挑臂根部和腹板间桥面板下缘的拉应力，横向应力对横向钢束位置的调整非常敏感。

4、多室截面恒载可按腹板数量均分。

其实横向构件的计算分实体横梁和箱梁框架，以上的1、2、4点均用于实体横梁计算，第3点用于桥面板计算。

不知道大家有什么见解？关于横梁计算，由于在立交和高架设计时经常碰到，我谈一点个人看法，如果没有张拉横梁预应力，各个腹板的受力极不均匀，位移大的腹板，弯距比较小，承受的力也比较小，但是张拉横向预应力以后，各个腹板受力就比较均匀了，一般边腹板的力与中腹板的力之比在1.0～1.2之间。

对于多箱室的，恒载应该考虑两种情况更安全，一个是各个腹板均分恒载，另一个是边腹板是中腹板的1.2倍，另外一个就是桥面上的活载，大家是按照横梁上均布还是，腹板均分？我一般是底板范围均分和腹板均分考虑，毕竟活载比重比较小，计算差别不是很大！我的观点是：1、活载应根据车辆荷载进行横向加载，考虑最不利组合。

2、计算宽度取实体厚度。

楼上的宽度的取法从理论上讲是正确的。

但是保守的取法可以留一定的安全储备。

请各位指正。

这种横梁在城市桥梁和互通立交中用的比较多,我接触过很多向,看了以上几位的留言,也谈一下我自己的看法:举个简单的例子:三跨连续梁的中间横梁,计算的第一步是先进行纵向计算,得出横梁处的活载反力和恒载反力,然后才能进行横梁计算.1、对恒载处理的方式有两种:一是把恒载均布加到横梁上箱梁腹板宽度范围内;另外一种就是认为腹板传力,把恒载加到腹板位置集中力加载;这两种方式我都计算过,第二种方式对设计来讲偏于保守,我实际计算时采取折中的办法,把恒载打0.9折.试想一下横梁两边箱梁防撞墙的重量不可能全部传到横梁上吧!2、对活载的处理方式：根据纵向计算得出的活载反力，算出每个车辆荷载的的轴重，然后自定义车辆荷载，根据实际的横向车辆布置进行活载加载。

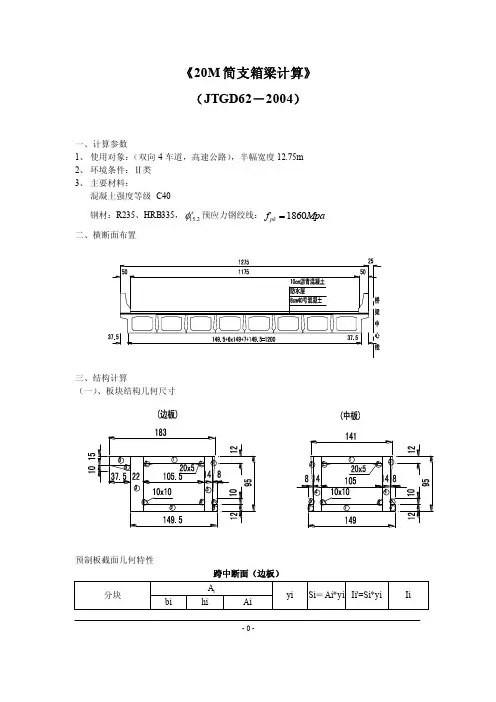
- 0 -《20M 简支箱梁计算》 （JTGD62－2004）一、计算参数1、 使用对象：（双向4车道，高速公路），半幅宽度12.75m2、 环境条件：Ⅱ类3、 主要材料：混凝土强度等级 C40钢材：R235、HRB335，15.2sφ预应力钢绞线：1860pk f Mpa =二、横断面布置三、结构计算（一）、板块结构几何尺寸预制板截面几何特性跨中断面（边板）- 1 -毛截面：314992.8943.857184isiS y cm A ===∑"4314992.8943.8513812438.23i i i I S y m ==⨯=∑'"402659390.3319638963.0413812438.238485915.14i i i I I I I m =+-=+-=∑∑∑换算截面：331440.2345.007364.74is iSy cm A ===∑234T s A I b td tα=+⎰ 221(145.5149.5)959595145.5149.522014+1812=+⨯++⨯+340.2237.520222677086600022333708cm +⨯⨯+＝＝（式中α高等学校教材“表2－4－3）跨中截面（中板）- 2 -毛截面：28595048.115944is iSy cm A ===∑'40i 2120672.7818882276.8628595048.117245895.14i i s I I I S y m =+-=+-⨯=∑∑∑换算截面：301123.3449.286110.74is iSy cm A ===∑'42120672.7820263050.9301123.3449.287544365.49i i i s I I I S y cm =+-=+-⨯=∑∑∑换22212121241()2T s A I S S h d S S S t t t t ==+++⎰221(141149)95951411492(1418)/21212=+⨯⨯+++4184100902521058834cm 11.87524.167⨯⨯+＝＝（二）荷载效应标准值 1、结构重力 1）板自重一期（预制板）326/r KN m =260.5915.45/q A K N ⨯ 中中＝r ＝＝- 3 -260.718418.68/m q A KN ⨯ 边边＝r ＝＝；二期（现浇铰缝、铺装层、护栏）铰缝混凝土 325/r K N m =[]250.950.730.08250.038 1.31/mq K N ⨯⨯⨯⨯⨯边＝(0.085)-(0.04)/2-(0.12+0.22)＝＝2 1.31 2.62/q K N m ⨯中＝＝ 铺装24(0.080.1) 1.5 6.48/q KN m ⨯+⨯中＝＝24(0.08 1.7850.11.375) 6.73/q KN m ⨯⨯+⨯边＝＝护栏按两侧刚性护栏对称布置，混凝土0.353/m m2(250.35)/8 2.19/q KN m ⨯⨯=栏＝1.31 6.7310.23/q KN m +∑边＝＝2.62 6.48 2.1911.29/q KN m ++∑中＝＝2）内力影响线- 4 -2、汽车荷载效应 1）公路Ⅰ级荷载均布荷载 10.5/k q K N m= 集中荷载 19.55180(1)238505k P K N -=⨯+=-当计算剪力时： 1.2238285.6k P KN =⨯= 2）冲击系数 结果基频 1f =（桥JTGD62－2004条文说明4－3条） 322/ 1.57710/c m G g NS m ==⨯1 5.05f Hz ==当11.514Hz f Hz ≤≤：0.1767ln 0.0157f μ=- （桥规JTGD60－2004，4.3.2式）所以 0.270μ= 1 1.270μ+= 3）汽车荷载横向分配系数3(~)44c l lk 修正的刚性横梁法 2ii ii ii iI a I R e Ia I β=±∑∑- 5 -221112ii iGl T E a I β=+∑∑ （式中G/E=0.4 ）20.0848660.072330.604iI=⨯+⨯=∑；20.0033460.21059 1.71iT =⨯+⨯=∑222222 5.250.084862(3.75 2.250.75)0.07246 4.6779 2.85317.531i ia I=⨯⨯+++⨯=+=∑边板 1 5.25a m = 11 5.250.084860.446I a =⨯=∴210.2579119.5 1.7110.4127.531β==<⨯+⨯ 符合规定 10.084860.08486 5.250.25790.14050.0153i i R e e ⨯=±⨯=±二列车影响线布载得：(0.22250.19500.17440.1470)/c k =+++= 0.5k 支＝ 沿桥纵向布置：- 6 -(三)持久状态承载能力极限状态计算1、正截面抗弯承载能力按《规范》5.2.2-1式计算00()2d cd x M f bx h γ≤-顶板：0b=183cm,t=12cm,h =91cm混凝土抗力：618.41830120 4.0410cd f bt N =⨯⨯=⨯由于顶板混凝土抗力大于钢筋抗力，混凝土受压区高度x 在顶板内，'112602800280791111.418.41830Pd P sd S cd f A f A x mm f b +⨯+⨯===⨯根据JTG D60－2004 基本组合表达式 （4.1.6－1）取用分项系数0γ――结构重要性系数，0γ=1.1；G γ――结构自重分项系数， G γ＝1.21Q γ――汽车荷载（含冲击力）的分项系数，取1Q γ＝1.4- 7 -001112()m nd Gi Gik Q Q k c Qj Qjk i j M S S S γγγγφγ===++∑∑[]1.11.2(887.86486.23) 1.4(10.270)613.123012.94K N m =⨯++⨯+⨯=⋅ 60111.4(18.41830111.4(910)3204.531022r cd x M f bx h N mm =-=⨯⨯-=⨯⋅03204.533012.94dK N m M K N mγ=⋅>=⋅ 符合规定 2、斜截面抗剪承载能力按《桥规》5.2.7－1式计算0d cs sb pb V V V V γ≤++ （荷载效应分项系数同正截面抗弯强度）计算斜截面位置距支点/2h ，d V 是斜截面受压端上由作用效应产生的最大剪力组合设计值：[]0 1.11.2(155.5385.17) 1.4(10.270)156.20623.22d V KN γ=⨯++⨯+⨯=1） 预制板截面尺寸应符合《规范》5.2.9式000.5100.51102140910821.86623.22d V b h KN KN γ--≤⨯⋅=⨯⨯⨯=>按《规范》5.2.10式检验斜截面要不要设箍筋330200.5100.510 1.25 1.652140910159.25d td V f bh KN γα--≤⨯=⨯⨯⨯⨯⨯⨯=对于板式受弯构件 1.25159.25=199.06K N <62⨯ 所以 预制板截面尺寸满足《规范》要求，但斜截面得设箍筋。

钢箱梁截面有效分布宽度的计算分析摘要：超大截面钢箱梁的桥位制造过程中，以基准控制、公差控制等措施，减小了钢箱梁的误差，确保了精度的控制，从而减少了实际装配中的失误。

节段预拼装的操作，有效确保了整体线型及端口匹配平顺，减少了后续的调整，大幅度提高了制造效率。

而提梁站与步履式顶推方式的选择，能有效进行施工控制，减小钢箱梁损伤及主体结构的整体受力，减少现场施工的工期流程与额外的运输等消耗，为以后相似类型的超大截面钢箱梁桥位的流水线设计提供了宝贵的经验。

本文主要分析钢箱梁截面有效分布宽度的计算。

关键词：钢箱梁;有效宽度;单箱宽度引言进行钢箱梁桥设计时首先要确定桥梁截面布置型式。

钢箱梁的截面设计要充分考虑翼缘有效分布宽度，尽可能使截面翼缘受力时全宽有效，减小剪力滞效应对翼缘板应力计算结果的影响。

钢箱梁截面单箱宽跨比不宜过大，否则截面不经济，容易造成钢材浪费。

以跨径30m～50m的多跨连续钢箱梁桥为例，对钢箱梁截面有效分布宽度进行分析研究。

1、设计主要过程（1）考虑地形、地质及道路总体要求，结合工程区域近远期规划等要素，合理确定连续梁的平面和跨径布置。

（2）根据桥梁周边场地、交通运输条件等合理拟定桥梁的施工工艺。

（3）根据该布置情况及相应受荷计算要求确定跨中及支点截面梁高，及梁底曲线，初步确定梁体构造。

（4）建立桥梁模型，对桥梁结构进行计算，根据计算结果调整梁截面尺寸、钢板厚度、连接方式、加劲肋等的布置位置、大小及方式，进一步确定梁体构造。

（5）对全桥结构进行核算，并满足各项构造措施要求。

2、钢箱梁桥位现场节段拼装现场组装钢箱梁节段，由多个且不同的板单元进行装配，最终在胎架上组成梁段。

胎架应使用专用胎架，提交设计要求并进行计算，之后通过马板对板单元进行固定。

为避免暴力拆卸对母材造成损伤，产生咬边及弧坑，现场人员应对马板相关的拆除进行监督，严禁以锤击的方式拆除马板，应在距母材表面1~3mm处用气割切除，并在切割完成后，对该位置进行打磨。

箱梁底板有效宽度计算公式在桥梁工程中，箱梁是一种常见的结构形式，其底板的有效宽度是一个重要的参数。

有效宽度的计算对于箱梁的设计和施工具有重要意义。

本文将介绍箱梁底板有效宽度的计算公式及其应用。

一、箱梁底板有效宽度的定义。

箱梁底板的有效宽度是指在计算箱梁受力时所采用的宽度。

在实际工程中，箱梁底板的宽度可能会受到各种因素的限制，如支座条件、荷载情况、变形要求等。

因此，需要对箱梁底板的有效宽度进行合理的计算和确定。

二、箱梁底板有效宽度的计算公式。

1. 根据规范。

《公路桥梁设计规范》中对箱梁底板的有效宽度计算给出了详细的规定。

在一般情况下，箱梁底板的有效宽度可以按照以下公式进行计算：b_eff = b 2a。

其中，b_eff为箱梁底板的有效宽度，b为箱梁底板的实际宽度，a为箱梁底板两侧的局部减薄厚度。

2. 考虑变形的影响。

在实际工程中，箱梁底板的有效宽度还需要考虑变形的影响。

在一定荷载作用下，箱梁底板会发生一定的变形，这时需要考虑箱梁底板有效宽度的变形影响。

一般情况下，变形对于箱梁底板的有效宽度的影响可以通过以下公式进行计算：b_eff = b 2a 2δ。

其中，δ为箱梁底板在荷载作用下的变形量。

三、箱梁底板有效宽度的应用。

1. 结构设计。

在进行箱梁结构设计时，需要根据箱梁底板的有效宽度进行受力分析和计算。

有效宽度的确定将直接影响箱梁结构的受力性能和安全性能。

因此，合理地确定箱梁底板的有效宽度对于结构设计具有重要的意义。

2. 施工施工。

在进行箱梁施工时，需要根据箱梁底板的有效宽度确定模板支撑和浇筑工艺。

有效宽度的确定将直接影响箱梁模板的搭设和浇筑施工的质量和效率。

因此，合理地确定箱梁底板的有效宽度对于施工具有重要的意义。

四、结语。

箱梁底板的有效宽度是一个重要的参数，其合理的计算和确定对于箱梁的设计和施工具有重要的意义。

在实际工程中，需要根据规范和实际情况综合考虑，确定合理的箱梁底板有效宽度。

希望本文介绍的箱梁底板有效宽度计算公式及其应用对于相关工程技术人员有所帮助。