当前位置：文档之家 › 运筹学 第2章 线性规划的图解法

运筹学 第2章 线性规划的图解法

  • 格式：ppt
  • 大小：604.00 KB
  • 文档页数：43

下载文档原格式

  / 43

合集下载

管理运筹学第二章 线性规划的图解法

管理运筹学第二章 线性规划的图解法

B、约束条件不是等式的问题：
若约束条件为 ai1 x1+ai2 x2+ … +ain xn ≤ bi 可以引进一个新的变量si ，使它等于约束右 边与左边之差 si=bi–(ai1 x1 + ai2 x2 + … + ain xn ) 显然，si 也具有非负约束，即si≥0， 这时新的约束条件成为 ai1 x1+ai2 x2+ … +ain xn+si = bi
第二章 线性规划 的图解法
一、线性规划的概念 二、线性规划问题的提出 三、线性规划的数学模型 四、线性规划的图解法 五、线性规划解的情况 六、LP图解法的灵敏度分析
一、线性规划的概念
线性规划Linear Programming 简称LP，是一 种解决在线性约束条件下追求最大或最小的 线性目标函数的方法。 线性规划的目标和约束条件都可以表示成线 性的式子。
max z 3 x1 2 x2
2 x1 x2 ≤ 10 设备B台时占用 s.t. x1 x2 ≤ 8 x , x ≥ 0 产量非负 1 2
决策变量 （decision variable） 目标函数 （objective function） 约束条件 （subject to）

-ai1
x1-ai2 x2- … -ain xn = -bi 。
例1.3：将以下线性规划问题转化为标准形式 Min f = 3.6 x1 - 5.2 x2 + 1.8 x3 s. t. 2.3 x1 + 5.2 x2 - 6.1 x3 ≤15.7 4.1 x1 + 3.3 x3 ≥8.9 x1 + x2 + x3 = 38 x 1 , x 2 , x3 ≥ 0

管理运筹学作业 韩伯棠第3版高等教育出版社课后答案

管理运筹学作业 韩伯棠第3版高等教育出版社课后答案

课程：管理运筹学管理运筹学作业第二章线性规划的图解法P23：Q2：（1）－（6）；Q3：(2)Q2：用图解法求解下列线性规划问题，并指出哪个问题具有唯一最优解，无穷多最优解，无界解或无可行解。

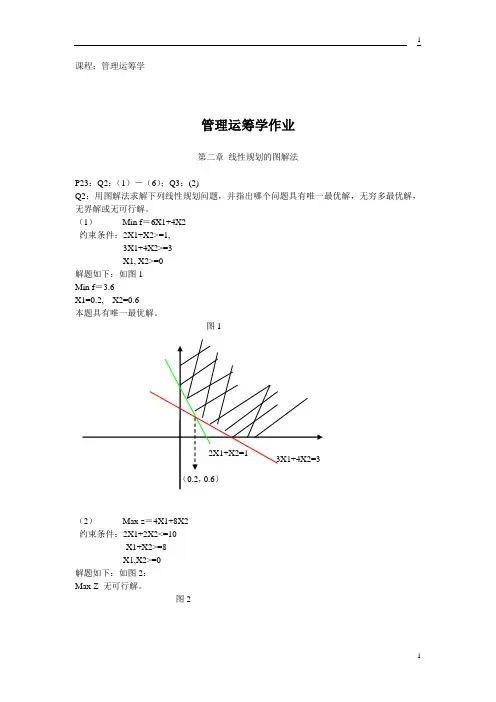
（1）Min f＝6X1+4X2约束条件：2X1+X2>=1,3X1+4X2>=3X1, X2>=0解题如下：如图1Min f＝3.6X1=0.2, X2=0.6本题具有唯一最优解。

图1（2）Max z＝4X1+8X2约束条件：2X1+2X2<=10-X1+X2>=8X1,X2>=0解题如下：如图2：Max Z 无可行解。

图2（3） Max z ＝X1+X2 约束条件 8X1+6X2>=24 4X1+6X2>=-12 2X2>=4 X1,X2>=0 解题如下：如图3： Max Z=有无界解。

图3（4） Max Z ＝3X1-2X2 约束条件：X1+X2<=1 2X1+2X2>=4 X1,X2>=0 解题如下：如图4： Max Z 无可行解。

图4(5)Max Z＝3X1+9X2 约束条件：X1+3X2<=22-X1+X2<=4X2<=62X1-5X2<=0X1,X2>=0解题如下：如图5：Max Z =66；X1=4 X2=6本题有唯一最优解。

图5(6)Max Z=3X1+4X2 约束条件：-X1+2X2<=8X1+2X2<=122X1+X2<=162X1-5X2<=0X1,X2>=0解题如下：如图6Max Z =30.669X1=6.667 X2=2.667本题有唯一最优解。

图6Q3：将线性规划问题转化为标准形式（2）min f＝4X1+6X2约束条件：3X1-2X2>=6X1+2X2>=107X1-6X2=4X1,X2>=0解题如下：1）目标函数求最小值化为求最大值：目标函数等式左边min改为max，等式右边各项均改变正负号。

运筹学线性规划图解法

运筹学线性规划图解法

引理1.线性规划问题的可行解X为基本可行解的充分 必要条件是X的正分量所对应的系数列向量是线性独立的. 证明:
必要性：已知X为线性规划的基本可行解，要证X的 正分量所对应的系数列向量线性独立。
因为X为基本解，由定义，其非零分量所对应的系数 列向量线性独立；又因为X还是可行解，从而其非零分量 全为正。
•有唯一解
例1： max z=2x1+ 3x2 s.t. x1+2x2≤8 4x1≤16 x1,x2≥0
画图步骤： 1、约束区域的确定 2、目标函数等值线 3、平移目标函数等值线求最优值
x2
可行域
(4,2) z=14
目标函数 等值线
x1
•有无穷多解
例2 max z =2x1+4x2 s.t. x1+2x2≤8 4x2 ≤ 12 3x1 ≤12 x1, x2 ≥0
X(0)=Σ α iX(i) α i0,Σ α i=1 记X(1),X(2), …,X(k)中满足max CX(i)的顶点为X(m)。于是，
k
k
CX (0) Ci X (i) Ci X (m) CX (m)
i 1
i 1
由假设CX(0)为最优解，所以CX(0)=CX(m)，即最优解可在顶点
充分性：已知可行解X的正分量所对应的系数列向量 线性独立，欲证X是线性规划的基本可行解。
若向量P1, P2,…, Pk线性独立,则必有k≤m；当k=m时， 它们恰构成一个基，从而X=（x1，x2,…,xk，0…0）为相 应的基可行解。K〈m时，则一定可以从其余的系数列向量 中取出m-k个与P1, P2,…, Pk构成最大的线性独立向量组， 其对应的解恰为X，所以根据定义它是基可行解。
§2 线性规划图解法

管理运筹学第二章线性规划的图解法

管理运筹学第二章线性规划的图解法

02
图解法的基本原理
图解法的概念
图解法是一种通过图形来直观展示线性规划问题解的方法。它通过在坐标系中绘 制可行域和目标函数，帮助我们理解问题的结构和最优解的位置。
图解法适用于线性规划问题中变量和约束条件较少的情况，能够直观地展示出最 优解的几何意义。
图解法的步骤
确定决策变量和目标函数
明确问题的决策变量和目标函数，以便在图 形中表示。
目标函数是要求最小化或最大化的函数，通常表示为 $f(x) = c_1x_1 + c_2x_2 + ldots + c_nx_n$。
04
约束条件是限制决策变量取值的条件，通常表示为 $a_1x_1 + a_2x_2 + ldots + a_nx_n leq b$或 $a_1x_1 + a_2x_2 + ldots + a_nx_n = b$。
LINDO是一款开源的线性规划求解器，用 户可以免费使用。
软件工具的使用方法
Excel
用户需要先在Excel中设置好线性规划模型，然后使 用“数据”菜单中的“规划求解”功能进行求解。
Gurobi/CPLEX/LINDO
这些软件通常需要用户先在软件界面中输入线性规划 模型，然后通过点击“求解”按钮进行求解。
实例三：分配问题
总结词
分配问题是指如何根据一定的分配原则 或目标，将有限的资源分配给不同的需 求方，以最大化整体效益。
VS
详细描述
分配问题在实际生活中广泛存在，如物资 分配、任务分配等。通过图解法，可以将 分配问题转化为线性规划模型，并利用图 形直观地展示最优解的资源分配方案。在 分配问题中，通常需要考虑不同需求方的 重要性和优先级，以及资源的有限性等因 素，以实现整体效益的最大化。

运筹学课件 第2章：线性规划的对偶理论

运筹学课件 第2章：线性规划的对偶理论

min w 16y1 36y2 65y3
90 y1 3 y 2 y1 2 y 2 5 y 3 70 y , y , y 0 1 2 3
原问题 A b C 约束系数矩阵
对偶问题 约束系数矩阵的转臵
约束条件的右端项向量 目标函数中的价格系数向量 目标函数中的价格系数向量 约束条件的右端项向量 Max z=CX Min w=Y’b 目标函数 AX≤b A’Y≥C’ 约束条件 X≥0 Y≥0 决策变量
若原问题为求极小形式的对称形式线性规划问题， 对偶问题应该具有什么形式？
Min w Y 'b A'Y C Y 0
max w Y 'b A'Y C Y 0
min z CX
Max z CX
AX b X 0
AX b X 0
min w 5 y1 4 y2 6 y3 4 y1 3 y2 2 y3 2 y1 2 y2 3 y3 3 3 y1 4 y3 5 2 y 7 y y 1 2 3 1 y1 0, y2 0, y3无约束
对偶问题 约束系数矩阵的转臵
目标函数中的价格系数向量
目标函数 约束条件
变量
Max z=CX m个 ≤ ≥ = n个 ≥0 ≤0 无约束
约束条件的右端项向量 目标函数 Min w=Y’b m个 ≥0 变量 ≤0 无约束 n个 ≥ 约束条件 ≤ =
【例2-3】写出下列线性规划问题的对偶问题
min 2x1 3x2 5x3 x4
1.初始表中单位阵在迭代后单纯形表中对应的位臵就是B-1 2.对于原问题的最优解，各松弛变量检验数的相反数恰好 是其对偶问题的一个可行解，且两者具有相同的目标函数 值。根据下面介绍的对偶问题的基本性质还将看到，若原 问题取得最优解，则对偶问题的解也为最优解。

管理运筹学_第二章_线性规划的图解法

管理运筹学_第二章_线性规划的图解法

线性规划中超过约束最低限的部分，称为剩余量。 记s1,s2为剩余变量，s3为松弛变量，则s1=0, s2=125,
s3=0，加入松弛变量与剩余变量后例2的数学模型变为 标准型： 目标函数： min f =2x1+3x2+0s1+0s2+0s3 约束条件： x1+x2-s1=350， x1-s2=125, 2x1+x2+s3=600, x1, x2, s1,s2,s3≥0.
阴影部分的每 一点都是这个线 性规划的可行解， 而此公共部分是 可行解的集合， 称为可行域。
B
X2=250
100
100
300
x1
B点为最优解， X1+X2=300 坐标为（50, 250）， Z=0=50x1+100x2 此时Z=27500。 Z=10000=50x1+100x2 问题的解： 最优生产方案是生产I产品50单位，生产Ⅱ产品250单位，可得 最大利润27500元。
Z=10000=50x1+50x2
线段BC上的所有点都代表了最优解，对应的最优值相 同： 50x1+50x2=15000。
10
3. 无界解，即无最优解的情况。对下述线性规划问题：
目标函数：max z =x1+x2 约束条件：x1 - x2≤1 -3x1+2x2≤6 x1≥0, x2≥0．
x2 -3x1+2x2=6 3
其中ci为第i个决策变量xi在目标函数中的系数， aij为第i个约束条件中第j个决策变量xj的系数， bj(≥0)为第j个约束条件中的常数项。
16
灵敏度分析
灵敏度分析：求得最优解之后，研究线性规划的

运筹学课件 第二章线性规划

运筹学课件 第二章线性规划

2020/11/23
广东工业大学管理学院
10
配料问题：由若干种不同价格、不同成分含量的原料，用 不同的配比混合调配出一些不同规格的产品，在原料的供 应量限制和保证产品成分含量的前提下，如何进行配料来 获取最大利润或使总成本最低。
投资问题：如何从不同的投资项目中选出一个投资方案， 使得投资的回报达到最大。
甲
乙
丙
A B C 加工费
x11 60%以上 x12 20%以下 x13 0.50
x21 15%以上 x22 60%以下 x23 0.40
x31 x32 50%以下 x33 0.30
售价
3.40
2.85
2.25
原料成本 2.00 1.50 1.00
限制用量 2000 2500 1200
设该厂每月生产甲品牌糖果(x11 x12 x13)千克，其中用原料A x11千克，用原料B x12千克，用原料C x13千克; 生产乙品牌糖果(x21 x22 x23)千克，其中用原料A x21千克，用原料B x22千克，用原料C x23千克; 生产丙品牌糖果(x31 x32 x33)千克，其中用原料A x31千克，用原料B x32千克，用原料C x33千克。
设一共植了y棵树，男生中有x1人挖坑, x2人栽树, x3人浇水； 女生中有x4人挖坑, x5人栽树, x6人浇水.
max z y
20x1 10x4 y 0 30x2 20x5 y 0
s.t.
25x3
x1
x2
15x6 x3
y 30
0
x4
x5
x6
20
x1, x2 , x3 , x4 , x5 , x6 , y 0
松弛变量
xs 2 (2x1 3x2 x3)

运筹学线性规划问题与图解法

运筹学线性规划问题与图解法



线性规划问题的一般形式
Max(min)Z=C1X1+ C2X2+…+CnXn a11X1+ a12X2+…+ a1nXn (=, )b1 a21X1+ a22X2+…+ a2nXn (=, )b2 … … … am1X1+ am2X2+…+ amnXn (=, )bm Xj 0(j=1,…,n)
简写式
Max(min)z c j x j
j 1 n
aij x j (, )bi , i＝1, 2,..., m st. j 1 x 0, j 1, 2,..., n j
n
向量式 Max(min)z CX
Pj x j (, )b st . j 1 x 0
min z C T X
线性规划的标准型
下列情况具体处理 若要求目标函数求最大化 若约束方程为不等式：非负松弛变量，非负 剩余变量 若变量不是非负：非正，自由变量， 右边为非正 任何形式的线性规划模型都可以化为标准型。

Ai

配料问题:每单位原料i含vitamin如下：
原料
1
A
4
B
1
Ｃ
0
每单位成本
2
2
3
6
1
1
7
2
1
5
6
4
每单位添 加剂中维生 素最低含量
2
5
3
8
12
14
8
求：最低成本的原料混合方案
解：设每单位添加剂中原料i的用量为 xi (i =1,2,3,4)
minZ= 2x1 + 5x2 +6x3+8x4 4x1 + 6x2 + x3+2x4 12

第二章 线性规划的图解法(简)

第二章 线性规划的图解法(简)

第二节 图解法
在线性规划中，对一个约束条件中没使用的资源或能力的大小称 之为松弛量。记为Si。
第二节 图解法
像这样把所有的约束条件都写成等式 ，称为线性规划模型的标准化，所得结果 称为线性规划的标准形式。
第二节 图解法
同样对于≥约束条件中，可以增加一些代表
最低限约束的超过量，称之为剩余变量，把≥约
第二章 线性规划的图解法
主要内容：
§1 问题的提出 （什么是线性规划） §2 图解法 §3 图解法的灵敏度分析
重点和难点
重点： （1）线性规划问题的主要概念 （2）线性规划问题的数学模型 （3）线性规划图解法的过程 （4）阴影价格的定义和灵敏度分析 难点： 灵敏度分析
第一节 问题的提出
约束条件对偶价格小于零时，约束条件
右边常数增加一个单位，就使得最优目
标函数值减少一个其对偶价格。
第三节 图解法的灵敏度分析
对目标函数值求最小值的情况下， 当对偶价格大于零时，约束条件右边常数增加 一个单位就使其最优目标函数值减少一个其对 偶价格； 当对偶价格等于零时，约束条件右边常数增加 一个单位，并不影响其最优目标函数值； 当对偶价格小于零时，约束条件右边常数增加 一个单位，就使得其最忧目标函数值增加一个 其对偶价格。
具有上述3个特征的问题为线性规划问题。
第一节 问题的提出
我们的仸务就是要选择一组或多组方案，使目
标函数值最大或最小。从选择方案的角度说，
这是规划问题。从使目标函数值最大或最小的
角度说，就是优化问题。
线性规划数学模型的一般表示方式
max(min) f ( x) c1 x1 c2 x2 cn xn a11 x1 a12 x2 a1n xn a x a x a x 21 1 22 2 2n n s.t. a x a x a x m2 2 mn n m1 1 x1 , x2 , , xn n : 变量个数 ; m : 约束行数 ; n m : 线性规划问题的规模 c j : 价值系数 ; b j : 右端项; aij : 技术系数 (, )b1 (, )b2 (, )bm 0

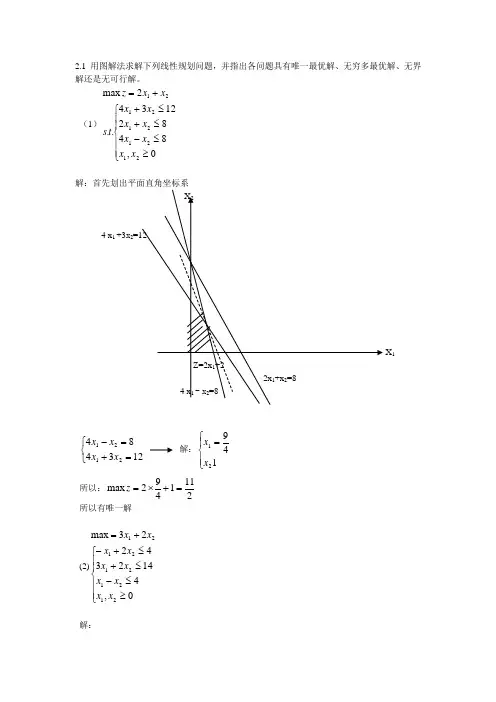
运筹学第二章答案.

运筹学第二章答案.

2.1 用图解法求解下列线性规划问题，并指出各问题具有唯一最优解、无穷多最优解、无界解还是无可行解。

（1）⎪⎪⎩⎪⎪⎨⎧≥≤-≤+≤++=0,84821234..2max 2121212121x x x x x x x x t s x x z解：首先划出平面直角坐标系4 x 1 +3x 2X 1⎩⎨⎧=+=-1234842121x x x x 解：⎪⎩⎪⎨⎧=14921x x 所以：2111492max =+⨯=z 所以有唯一解(2)⎪⎪⎩⎪⎪⎨⎧≥≤-≤+≤+-+=0,414234223max 2121212121x x x x x x x x x x 解：2=41⎩⎨⎧=+=+-1423422121x x x x 解得：⎪⎪⎩⎪⎪⎨⎧==4132521x x 所以:144132253max =⨯+⨯=z 因为直线02321=+x x 与直线142321=+x x 平行， 所以有无穷多最优解，max z=14（3） ⎪⎩⎪⎨⎧≥≤+-≤-+=0,432..32max 21212121x x x x x x t s x x z 解：（4）⎪⎩⎪⎨⎧≥-≤-≥-+=0,330..max 21212121x x x x x x t s x x z解：2.2将下列线性规划问题化为标准形式(1) s.t.⎪⎩⎪⎨⎧≥≤≤-+-=++-+-=无约束321321321321,0,0624322min x x x x x x x x x x x x z (2)⎪⎪⎩⎪⎪⎨⎧≤≥-=-+-≤+-≥--+=0,0232132..23min 3213213132321x x x x x x x x x x t s x x x z 无约束， 解：（1）令011≥-=x x )0'','('''33333≥-=x x x x x则上述形式可化为：)'''(32'2m ax 3321x x x x z --+=⎪⎩⎪⎨⎧≥=+--+=-++0,'',',,'6)'''('24)'''('..43321433213321x x x x x x x x x x x x x x t s（2）⎪⎪⎩⎪⎪⎨⎧≤≥-=-+-≤+-≥--+=0,0232132..23min 3213213132321x x x x x x x x x x t s x x x z 无约束， 解：令33'x x -= )0','','(322≥x x x 则上述形式可化为：')'''(23m ax 3221x x x x z ----=⎪⎪⎩⎪⎪⎨⎧≥=---=+--=+---0,,','',',2')'''(321')'''(3')'''(2..543221322153224322x x x x x x x x x x x x x x x x x x t s 2.3. 在下列线性规划问题中，找出所有基解，指出哪些是基可行解并分别代入目标函数，比较找出最优解。

北交大交通运输学院《管理运筹学》知识点总结与例题讲解第2章 线性规划

北交大交通运输学院《管理运筹学》知识点总结与例题讲解第2章 线性规划

第二章线性规划教学目的：了解线性规划的基本概念，理解线性规划最优化原理、单纯形法原理，掌握单纯形法及其矩阵描述、人工变量法、，能够对简单的问题建模。

教学重点：线性规划的含义、性质；线性规划问题的求解方法——图解法、单纯形法。

线性规划模型的建立非标准型线性规划问题转化为标准线性规划问题；线性规划问题的图解法；解的存在情况判断；大M法；两阶段法；单纯形法的矩阵表示；教学难点：单纯形法的求解思想、矩阵表示、对偶理论、对偶单纯形法以及灵敏度分析。

学时： 8学时2.1 线性规划(Linear Programming,LP)问题及其数学模型（1学时）我们应用数学规划模型求解实际问题中，将实际问题抽象成数学模型，然后再对其求解。

2.1.1线性规划问题提出我们用一个简单例子来说明如何建立数学规划问题的数学模型。

例2.1 某家具厂生产桌子和椅子两种家具，有关资料见表2－1。

解：用数学语言来描述生产计划安排问题，这个过程称为建立其数学模型，简称建模。

设：①桌子、椅子生产的数量分别为x1，x2，称为决策变量。

因为产量一般是一个非负数，所以有x1，x2≥0，称非负约束。

②限制条件为木工和油漆工的加工时间约束了产品的生产量x1，x2。

约束如下：4x1＋3x2≤1202x1＋x2≤50③生产桌子、椅子x 1，x 2所得总收入为Z ，显然Z ＝50x 1＋30x 2。

我们希望总收入值能达到最大，这个关系用公式表达为max Z ＝50x 1＋30x 2 把上述所有数学公式归纳如下12121212max .0z 50x 30x 4x 3x 120s t 2x x 50x x =++≤⎧⎪+≤⎨⎪≥⎩，这就是一个最大化的线性规划模型。

例 2.2（运输工具的配载问题）有一辆运输卡车，载重2.5t ，容积183m ，用来装载如下的两种货物：箱装件125kg/个、0.43m /个；包装件20kg/个、1.53m /个。

问：如何装配，卡车所装物件个数最多？解 根据题意，设箱装件1x 个，包装件2x 个，那么需要满足条件：体积约束 120.4 1.518x x +≤重量约束 12125202500x x +≤非负约束12,0x x ≥目标要求 max z=12x x +我们对上面的式子稍作整理，便得到下面的形式：max z=12x x +1212120.4 1.518125202500,0x x x x x x +≤⎧⎪+≤⎨⎪≥⎩ 上述两例中所提出的问题，最终都归结为在变量满足线性约束条件的前提下，求使线性目标函数最大或最小的问题，这种问题称为线性规划问题。

管理运筹学 线性规划的图解法课件

管理运筹学 线性规划的图解法课件

线性规划的应用领域
生产计划
线性规划可以用于制定生产计划，优 化资源配置，提高生产效率。
物流优化
线性规划可以用于优化物流配送路线 、车辆调度等问题，降低运输成本。
金融投资
线性规划可以用于金融投资组合优化 ，实现风险和收益的平衡。
资源分配
线性规划可以用于资源分配问题，如 人员、资金、设备等资源的合理分配 ，提高资源利用效率。
束条件。
线性规划的目标是在满足一系列 限制条件下，使某一目标函数达
到最优值。
线性规划问题通常表示为求解一 组变量的最优值，使得这些变量 满足一系列线性等式或不等式约
束。
线性规划的数学模型
线性规划的数学模型由决策变量、目标函数和约束条 件三部分组成。
输标02入题
决策变量是问题中需要求解的未知数，通常表示为 $x_1, x_2, ldots, x_n$。
01
03
约束条件是限制决策变量取值的条件，通常表示为 $a_1x_1 + a_2x_2 + ldots + a_nx_n leq b$或 $a_1x_1 + a_2x_2 + ldots + a_nx_n = b$。
04
目标函数是问题要优化的函数，通常表示为$f(x) = c_1x_1 + c_2x_2 + ldots + c_nx_n$。
03
绿色发展与线性规 划的结合
将可持续发展理念融入线性规划 ，实现资源节约、环境友好的发 展目标。
THANKS
[ 感谢观看 ]
约束条件
生产计划问题通常受到资源限制、市场需求和生 产能力等约束条件的限制。
详细描述
生产计划问题通常涉及到如何分配有限的资源， 以最大化某种目标函数（如利润）。通过图解法 ，我们可以将约束条件和目标函数在二维平面上 表示出来，从而找到最优解。

运筹学线性规划

运筹学线性规划
其次线性规划模型必须满足如下两个要求： ① 目标函数必须是决策变量的线性函数； ② 约束条件必须是含决策变量的线性等式或不等式。
运筹学建模步骤: 识别问题 定义决策变量
建立约束条件 建立目标函数
整理课件
2.2 线性规划模型的一般形式和标准形式
2.2.1 线性规划的一般模型
为了讨论一般的线性规划问题的求解。我们先给出线性规 划模型的一般形式如下：
max(或min)z CX
n
s.t. j1
Pj x j
(或 ，或)b
X 0
其中
x1
a1j b1
Xx2,Cc1 c2 cn,Pj a2j,bb2
xn
amj bm
整理课件
用矩阵的记号可以将线性规划模型一般形式写成：
max(或min)z CX
AX (或，或)b s.t.X 0
其中 X, C, b 同上，而矩阵 A 是由各约束条件的系数（技术
养分
饲料
A
B
C
M
0.5
0.2
0.3
D
价格
0
300
N
0.1
0.3
0.4
0.2
200
每头日需 10
5
8
7
答案：设购买M饲料x1，N饲料x2
Min Z=300 x1 +200x2 0.5 x1 +0.1x2≥10
0.2x1 +0.3x2 ≥5
s.t.
0.3x1 +0.4x2 ≥8
0.2x2 ≥7
x1 , x2≥0 整理课件
x1 2 x2 5
s.t.
2
4
x1 x1
x2 4 3x2 9

运筹学

运筹学

(a)
(b)
(c)
(d)
(e)
图中红粗线和红点是顶点. 图中红粗线和红点是顶点. 红粗线 是顶点
3. 线性规划基本定理
定理1 定理 1
若线性规划问题存在可
行解,则问题的可行域是凸集. 行解,则问题的可行域是凸集.
方法1 证 (方法1) 若满足线性规划约束条件 下面给予证明. C内,下面给予证明. 设 X1 = (x11, x12,, x1n )T 即
一,关于标准型解的若干基本概念
线性规划问题 :
max z =
∑c
j =1
n
j
xj ( i = 1, , m ) ( j = 1, , n )
(2.1) (2.2) (2.3)
n ∑ a ij x j = bi j =1 x ≥ 0 j
可行解:满足上述约束条件( 可行解:满足上述约束条件(2.2),(2.3)的解 X = (x1, xn )T ,称为线性 , 规划问题的可行解.全部可行解的集合称为可行域 可行域. 规划问题的可行解.全部可行解的集合称为可行域. 最优解:使目标函数( 最优解:使目标函数(2.1)达到最大值的可行解称为最优解. 达到最大值的可行解称为最优解. 基:设 A 为约束方程组(2.2)的 m×n 阶系数矩阵,(设n>m),其秩 为约束方程组( 阶系数矩阵, m), 是矩阵A中的一个m 阶的满秩子系数矩阵, 为m,B是矩阵A中的一个m×m阶的满秩子系数矩阵,称B是线性规划问题的 一个基. 一个基.
若线性规划问题存在可行解, 则所有可行解的集合——可 若线性规划问题存在可行解, 则所有可行解的集合——可 —— 是凸集. 行域 C = {X| AX= b,X ≥0 }是凸集. 是凸集 证明: 方法 证明:(方法 2) 设 X1∈C,X2 ∈C,则 A X1=b,A X2=b,X1 ≥0,X2 ≥0 , , , 在 X1, X2 连线上任取一点 X 故 AX =A[αX 1 + ( 1 α ) X 2 ] =αAX 1 + ( 1 α ) AX 2 = b

第二章 线性规划的图解法

第二章 线性规划的图解法

例2.某工厂在计划期内要安排Ⅰ、Ⅱ两种产 品的生产，已知生产单位产品所需的设备台 时及A、B两种原材料的消耗、资源的限制， 如下表：
设备 原料 A 原料 B 单位产品获利 Ⅰ 1 2 0 50 元 Ⅱ 1 1 1 100 元 资源限制 300 台时 400 千克 250 千克
问题：工厂应分别生产多少单位Ⅰ、Ⅱ 产品才能使工厂获利最多？
第二章 线性规划的图解法
问题1具体数据如表所示：
资源 单耗 资源 煤(t) 电(kw.h) 油(t) 单位产品价格 9 4 3 7 4 5 10 12 360 200 300 产品 甲 乙 资源限量
提出和形成问题
建立模型
求解
结果的分析和应用
第二章 线性规划的图解法
在本例中
决策变量： 甲、乙产品的计划产量，记为x1 ，x2； 目标函数： 总收入记为f,则 f=7x1 +12x2 ，为体现对其求极大化， 在f 的前面冠以极大号Max，
第二章 线性规划的图解法 例2：.某公司由于生产需要，共需要A，B两种原料至 少350吨（A，B两种材料有一定替代性），其中A原 料至少购进125吨。但由于A，B两种原料的规格不同， 各自所需的加工时间也是不同的，加工每吨A原料需 要2个小时，加工每吨B原料需要1小时，而公司总共 有600个加工小时。又知道每吨A原料的价格为2万元， 每吨B原料的价格为3万元，试问在满足生产需要的 前提下，在公司加工能力的范围内，如何购买A，B 两种原料，使得购进成本最低？
第二章 线性规划的图解法
★线性规划模型的三个基本要素：
（也是所有规划问题的三个基本要素）：
（1）决策变量：甲、乙产品的产量x1 ，x2 决策变量：需要决策的量，即等待求解的未知数。 （2）目标函数：总收入最大，Max f = 7 x 1 +12 x 2 目标函数：想要达到的目标，用决策 变量的表达式表示。 （3）约束条件： 约束条件：由于资源有限，为了实现 目标有哪些资源限制，用决策变量的 等式或不等式表示。

运筹学第四版第二章线性规划及单纯形法

运筹学第四版第二章线性规划及单纯形法

方案的制定受到那些现实条件制约：
确定约束条件
人力资源（劳动力）的限制： 9x1 4x2 360
设备工时的限制：
4x1 5x2 200
原材料资源的限制：
3x1 10x2 300
此外，决策变量的取值不应为负值即 x1 0, x2 0
6
综上所述，我们得到了这个问题的数学模型
目标函数 约束条件
大？
项目
Ⅰ
设备A (h)
0
设备B (h)
6
调试工序(h) 1
利润（元） 2
Ⅱ 每天可用能力
5
15
2
24
表1-2
1
5
1
12
其数学模型为：
max Z 2x1 x2
5x2 15
6xx11
2x2 x2
24 5
x1, x2 0
13
例3：捷运公司在下一年度的1～4月份的4个月内拟租用仓库
堆放物资。已知各月份所需仓库面积列于下表1-3。仓库租
借费用随合同期而定，期限越长，折扣越大，具体数字见表
1-4。租借仓库的合同每月初都可办理，每份合同具体规定
租用面积和期限。因此该厂可根据需要，在任何一个月初办
理租借合同。每次办理时可签一份合同，也可签若干份租用
面积和租用期限不同的合同。试确定该公司签订租借合同的
最优决策，目的是使所租借费用最少。
14
max Z 70 x1 120 x2
9x1 s.t. 43xx11
x1,
4x2 5x2 10x2 x2 0
360 200 300
资源约束
非负约束
其中 约束条件可记 s.t (subject to), 意思为“以… 为条件“、”假定“、”满足“之意。

运筹学课件1-2-1线性规划图解法

运筹学课件1-2-1线性规划图解法

x2
4x1 ≤ 16 C D
| 1 | 2 | 3 | 4
4 x2 ≤ 16
最优解 (4, 2)
x1 + 2x2 ≤ 8
| 6 | 7 | 8 | 9
A
0
E
| 5
x1 下页 返回
上页
图解法求解步骤
• 由全部约束条件作图求出可行域； 由全部约束条件作图求出可行域； 可行域 • 作目标函数等值线，确定使目标函数最 作目标函数等值线， 等值线
E (8,0)
| 6
| 8
| | 10 12
| | | 14 16 18
x1 下页 返回
上页
练习） 图解法 —（练习）
18 — 16 — 14 — 12 — 10 — B 8—
x2
2x1 + x2 ≤ 16 2x1 + 2x2 ≤ 18 C 4x1 + 6x2 ≤ 48 D
| 2 | 4 | 6 | 8 | | 10 12 | | | 14 16 18
上页 下页 返回
x2
6 ① ③ 4
④
2
(4,2)
Zmax ②
0
2 Z=0
4 Z=6
6
8
x1
返回
上页
下页
练习： 练习：
用图解法求解LP问题
Max Z = 34 x1 + 40 x2
4 x1 + 6 x2 ≤ 48 2 x1 + 2 x2 ≤ 18 2 x1 + x2 ≤ 16 x1、 x2 ≥ 0
A
x1 下页 返回
上页
练习） 图解法 —（练习）
18 — 16 — 14 — 12 — 10 — B 8—
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
管理运筹学
朱晓辉 管理科学与工程
管理运筹学
2-1
第二章 线性规划的图解法
教学目标：
• 掌握线性规划的数学模型，能够结合问 题列出模型
• 理解图解法求解 • 了解图解法的灵敏度分析
管理运筹学
2-2
第二章 线性规划的图解法
• §1 问题的提出 • §2 图解法 • §3 图解法的灵敏度分析
管理运筹学
管理运筹学
2-8
§2 图 解 法
对于只有两个决 例1.目标函数：
策变量的线性规划问
Max z = 50 x1 + 100 x2
题，可以在平面直角 约束条件：
坐标系上作图表示线 性规划问题的有关概 念，并求解。
下面通过例1详细讲 解其方法：
s.t.
x1 + 2 x1 +
x2 ≤ 300 (A) x2 ≤ 400 (B) x2 ≤ 250 (C) x1 ≥ 0 (D) x2 ≥ 0 (E)
2-3
第二章 线性规划的图解法
在管理中一些典型的线性规划应用: • 合理利用线材问题：如何在保证生产的条件下，下料最少 • 配料问题：在原料供应量的限制下如何获取最大利润 • 投资问题：从投资项目中选取方案，使投资回报最大 • 产品生产计划：合理利用人力、物力、财力等，使获利最
大 • 劳动力安排：用最少的劳动力来满足工作的需要 • 运输问题：如何制定调运方案，使总运费最小
• 一般形式:
目标函数：
约束条件：
Max （Min） z = c1 x1 + c2 x2 + … + cn xn
s.t. aa…x2m11a…1，1xx111xx++21a，+a2…m2a…2…1x2x2，x2+2+x…+n……+≥+a+0a2nam1xnnnxxnn≤≤（≤（（==, =,≥,≥）≥））bb2bm1
2 x1 + x2 +s3= 600
x1 , x2 , s1, s2, s3 ≥ 0
管理运筹学
2-24
§3 图解法的灵敏度分析
线性规划的标准化
• 一般形式
目标函数： 约束条件：
• 标准形式
Max （Min） z = c1 x1 + c2 x2 + … + cn xn
s.t.
…aa…1211
xx11
管理运筹学
2-26
§3 图解法的灵敏度分析
1.极小化目标函数的问题： 设目标函数为
Min f = c1x1 + c2x2 + … + cnxn (可以)令 z ＝ -f ，
则该极小化问题与下面的极大化问题有相同的最优解，
即 Max z = - c1x1 - c2x2 - … - cnxn
但必须注意，尽管以上两个问题的最优解相同，但它们 最优解的目标函数值却相差一个符号，即
把所有的约束条件都写成等式，称为线性规划模型的 标准化。
管理运筹学
2-20
进一步讨论
例2 某公司由于生产需要，共需要A，B两种原料至少350 吨（A，B两种材料有一定替代性），其中A原料至少购进125 吨。但由于A，B两种原料的规格不同，各自所需的加工时间 也是不同的，加工每吨A原料需要2个小时，加工每吨B原料需 要1小时，而公司总共有600个加工小时。又知道每吨A原料的 价格为2万元，每吨B原料的价格为3万元，试问在满足生产需 要的前提下，在公司加工能力的范围内，如何购买A，B两种 原料，使得购进成本最低？
• 对于“ ”约束条件，可以增加一些最低
限约束的超过量，称之为剩余变量。从而把
“ ” 约束条件变为等式约束条件。
管理运筹学
2-23
• 加了松弛变量和剩余变量后的例2的数学模型 为：
目标函数： Min f = 2x1+3x2+0s1+0s2+0s3
约束条件：
s.t.
x1+ x2 - s1= 350
x1 -s2 = 125
2-18
§2 图 解 法
• 在最优生产方案下资源消耗的情况：把x1=50, x2=250代入约束条件得
• 设备台时：1*50+1*250=300 • 原料A：2*50+1*250=350 • 原料B：0*50+1*250=250
• 说明：生产50单位Ⅰ产品和250单位Ⅱ产品将消 耗完所有可能的设备台时数及原料B，但对原料A则 还剩余50千克。
线性规划的组成：
•目标函数 Max F 或 Min F
•约束条件 s.t. (subject to) 满足于
•决策变量 用符号来表示可控制的因素
管理运筹学
2-4
§1 问题的提出
例1. 某工厂在计划期内要安排Ⅰ、Ⅱ两种产品的生产，已知生产单位产 品所需的设备台时及A、B两种原材料的消耗、资源的限制，如下表：
x2
z=10000=50x1+100x2
AB C
z=0=50x1+100x2
E
z=27500=50x1+100x2
z=20000=50x1+100x2
D
x1
图2-2
管理运筹学
2-14
§2 图 解 法
• 重要结论：
– 如果线性规划有最优解，则一定有一个可行域的顶 点对应一个最优解；
– 无穷多个最优解。若将例1中的目标函数变为max z优=解50；x1+50x2，则线段BC上的所有点都代表了最
管理运筹学
2-21
进一步讨论
解：目标函数： Min f = 2x1 + 3 x2 约束条件：
s.t.
x1 + x2 ≥ 350
x1 ≥ 125
2 x1 + x2 ≤ 600
x1 , x2 ≥ 0
采用图解法。如下图：得Q点坐标（250，100）为最优解。
x2
x1 =125
600
500
2x1+3x2 =1200
xx22++
… …
+ +
aa12nn
xxnn
= =
bb12
axm11，x1x+2 ，am…2 x，2 +xn…≥+0a，mnbxin≥0= bm
管理运筹学
2-25
§3 图解法的灵敏度分析
可以看出，线性规划的标准形式有如下四个特 点：
– 目标最大化； – 约束为等式； – 决策变量均非负； – 右端项非负。 对于各种非标准形式的线性规划问题，我们总可 以通过以下变换，将其转化为标准形式:
• 可行域的几何形状由于问题不同可以千变万 化，但可行域的几何结构是凸集
• 要求集合中的任何两点的连线段落在这个集 合中
管理运筹学
2-13
§2 图 解 法
到（一4条）直目线标，函直数线z上=5的0每x1+一1点00都x具2，有当相z取同某的一目固标定函值数时值得， 称之为“等值线”。平行移动等值线，当移动到B点时，z 在可行域内实现了最大化。A，B，C，D，E是可行域的顶 点，对有限个约束条件则其可行域的顶点也是有限的。
Min f ＝ - Max z
管理运筹学
2-27
§3 图解法的灵敏度分析
2、约束条件不是等式的问题： 设约束条件为
ai1 x1+ai2 x2+ … +ain xn ≤ bi 可以引进一个新的变量s ，使它等于约束右边与左
边之差
s=bi–(ai1 x1 + ai2 x2 + … + ain xn ) 显然，s 也具有非负约束，即s≥0，
++…aa…1222
xx22++
… …
+ +
aa12nn
xxnn
≤ ≤
（ （
=, =,
≥ ≥
））bb12
x1a，m1xx21，+ a…m2，x2xn+
…+ ≥0
amn
xn
≤
（
=,
≥
）bm
目标函数： 约束条件：
Max z = c1 x1 + c2 x2 + … + cn xn
s.t.
……aa1211
xx11 ++…aa…1222
x1，x2≥0．
(4 ）
max z=3x1+9x2；
约束条件：
x1+3x2≤22，
-x1+x2≤4，
x2≤6，
2x1-5x2≤0，
x1，x2≥0
管理运筹学
2-17
答案
• （1）有唯一解x1 = 0.2, x2= 0.6函数值为 3.6 • （2）无可行解 • （4） 无可行解 • （5）无穷多解
管理运筹学
– 无界解。即可行域的范围延伸到无穷远，目标函数 值可以无穷大或无穷小。一般来说，这说明模型有 错，忽略了一些必要的约束条件；
– 无可行解。若在例1的数学模型中再增加一个约束 条足件约束4x条1+件3x的2≥解1，20当0，然则也可就行不域存为在空最域优，解不了存。在满
管理运筹学
2-15
练习题
• 2. 用图解法求解下列线性规划问题，并指出哪 个问题具有惟一最优解、无穷多最优解、无界解或 无可行解．
பைடு நூலகம்
X1=0
x1
管理运筹学
x1
2-10
§2 图 解 法
（2）对每个不等式(约束条件)，先取其等式在坐标系中 作直线，然后确定不等式所决定的半平面。
300
200
x1+x2=300