下载文档原格式
工业机器人正运动和逆运动学LOREM IPSUM DOLOR1工业机器人正运动和逆运动学为了方便研究使工业机器人的运动控制问题简单易懂，我们需要研究机器人 末端执行器（工具）位姿。
2工 业机器人正运动和逆运动学为了使问题简单易懂，先以二自由度的机器人手爪为例 来说明。
图 5⁃14所示为二自由度 机器人手部的连杆机构。
由于 其运动主要由连杆机构来决定，所以在进行机器人运动学分析 时,大多数是把驱动器及减速器 的元件去除后来进行分析的。
图5-14 二自由度机械手的正运动学工业机器人正运动和逆运动学图 5⁃14中的连杆机构是两杆件通过转动副连接的关节结构， 通过确定连杆长 度了l1、l2 以及关节角θ1、θ2，可以定义该连杆机构。
在分析机器人末端手爪的运动时， 若把作业看作主要依靠机器人手爪来实现 的，则应考虑手爪的位置（图中点Ｐ的位置）。
一般场合中，手爪姿势也表示手指位置。
从几何学的观点来处理这个手爪位 置与关节变量的关系称为运动学(Kinematics)。
工业机器人正运动和逆运动学引入矢量分别表示手爪位置r 和关节变量θ， 即,rx y 1 2 因此，可以利用上述两个矢量来描述图 5-13 所示的二自由度机器人的运动学问题工业机器人正运动和逆运动学手爪位置r在x，y轴上的分量， 按几何学可表示为x l1 cos1 l2 cos(1 2 ) y l1 sin1 l2 sin(1 2 )(5 1) (5 2)工业机器人正运动和逆运动学用矢量表示这个关系式， 其一般可表示为r f ( )(5 - 3)式中，ｆ表示矢量函数。
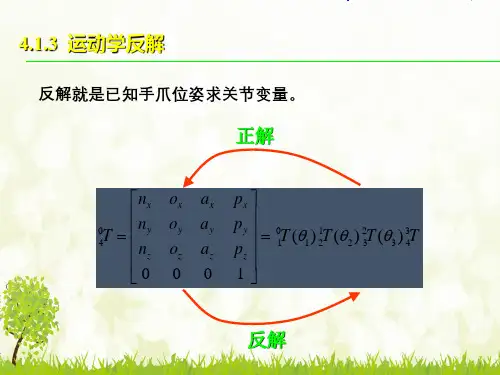
已知机器人的关节变量θ，求其手爪位置 ｒ 的 动学问题称为正运动学(directkinematics)。
式(5-3)称为运动方程式。
工业机器人正运动和逆运动学如果给定机器人的手爪位置ｒ，求能够到达这个预定位置的机 关节变量θ的运动学问题称为逆运动学(inversekinematics)。
从手部位姿到关节变量—运动学逆问题操作机的手臂解r -θ对于 操作机，其逆变换就是由表示手部位姿的齐次矩阵求操作机的两个关节变量。
r -θ由手坐标系到基座坐标系的齐次矩阵可以表示为21A A T H B =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000100001000011000010000cos sin 00sin cos 1000r P a o n P a o n P a o n z zzz y y y y x x x x θθθθ令上面矩阵的对应元素分别相等 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡10-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡θθθθθθsin cos 010000cos sin 00sin cos 1001000000r r P P o o n n y x y x yx cos x r P θ=sin yr P θ=tan yx P P θ=arctan yxP P θ=所以⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--1000010000cos sin 00sin cos 1000010000cos sin 00sin cos 1θθθθθθθθ令其中的对应元素分别相等，则可以得到cos sin x y r P P θθ=+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-10000100001000110010000001000010000cos sin 00sin cos r P P o o n n y x y x y x θθθθ令关节多了则不然！其实问题很简单P xP yrθθcos xr P θ=sin y r P θ=正解：cos sin x y r P P θθ=+arctan y x P P θ=逆解：手部姿态角的确定手部的姿态可以用绕x ，y ，z 轴依次转动侧摆，俯仰和横滚获得。
),(),(),(1x y OH z x Rot y Rot T z Rot ΦΦ=Φ-),(),(),(),,(x y z z y x OH x Rot y Rot z Rot RPY T Φ⋅Φ⋅Φ=ΦΦΦ=等式左式与右式对应元素相等，最终可得()⎪⎩⎪⎨⎧=ΦΦ+Φ-=ΦΦ-ΦΦ-Φ=Φx y zz y z x z y z x z y z y z x x n n n n n o o a a /arctan )]sin cos /(arctan[)]sin cos /()cos sin arctan[(6关节操作机的手臂解6关节操作机位置运动学逆问题就是由描述手部位姿的齐次矩阵BTH 求解构成手臂的六个关节角 、 、 、 、 、 ，这一逆问题又称为手臂解。
