距离保护的整定计算
- 格式:doc
- 大小:155.78 KB
- 文档页数:6




距离保护的整定计算距离保护的整定计算⼀、距离保护第⼀段 1.动作阻抗(1)对输电线路,按躲过本线路末端短路来整定,即取AB K dzZ k Z '='?12.动作时限0≈'t 秒。
⼆、距离保护第⼆段1.动作阻抗(1)与下⼀线路的第⼀段保护范围配合,并⽤分⽀系数考虑助增及外汲电流对测量阻抗的影响,即()BC k fz AB k dzZ K K Z K Z '+''=''?1式中fz K 为分⽀系数min ???? ??=ABBCfz II K(2)与相邻变压器的快速保护相配合()B fz AB k dzZ K Z K Z +''=''?1取(1)、(2)计算结果中的⼩者作为1?''dzZ 。
2. 动作时限保护第Ⅱ段的动作时限,应⽐下⼀线路保护第Ⅰ段的动作时限⼤⼀个时限阶段,即12CABA '图3-50 电⼒系统接线图AZ 'BABZ BCZ Z 'Z ''Z '''00.5tZ 'Z ''Z '''00.5t3AZ 12CABA '图3-50 电⼒系统接线图AZ 'BABZ BCZ Z 'Z ''Z '''00.5tZ 'Z ''Z '''00.5t3AZt t t t ?≈?+'=''213.灵敏度校验5.1≥''=ABdzlm Z Z K如灵敏度不能满⾜要求,可按照与下⼀线路保护第Ⅱ段相配合的原则选择动作阻抗,即()2.dz fz AB k dzZ K Z K Z ''+''=''这时,第Ⅱ段的动作时限应⽐下⼀线路第Ⅱ段的动作时限⼤⼀个时限阶段,即三、距离保护的第三段1.动作阻抗按躲开最⼩负荷阻抗来选择,若第Ⅲ段采⽤全阻抗继电器,其动作阻抗为min.1.1fh zqh k dzZ K K K Z '''='''式中2.动作时限保护第Ⅲ段的动作时限较相邻与之配合的元件保护的动作时限⼤⼀个时限阶段,即t t t ?+'''='''23.灵敏度校验作近后备保护时5.11.≥'''=ABdzlm Z Z K 近作远后备保护时2.1≥+'''=BCfz ABdzlm Z K Z Z K 远式中,K fz 为分⽀系数,取最⼤可能值。


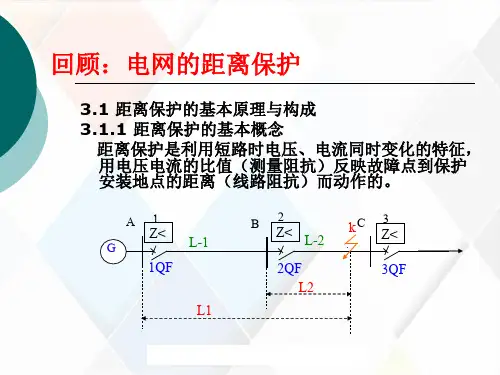
距离保护整定计算I 在图(1)所示网络中,各线路均装有距离保护,试对其中保护1的相间短路保护ΙΠ 段进行整定计算。
其中E1的电压为115KV ,最大阻抗为25ΙΠΩ最小阻抗为20Ω.E2的最大阻抗为30Ω 最小阻抗为25Ω E3的最大阻抗为20Ω最小阻抗为15。
已知线路a----b 的最大负荷电流Ω=max .D I 350A ,功率因数cos ϕ=0.9,各线路每公里阻抗z1=km Ω4.0 ,阻抗角l ϕ=70,,电动机的自启动系数=1.5,正常时母线最低工作电压取等于0.9,t ,。
,85.0=Ιrel K ,8.0=Πrel K 2.1=ΙΠrel K 15.1=re K ss K min .L U N U s 5.0312=s t 5.1310=解 :1. 有关各元件阻抗值的计算线路1—2的正序阻抗 )(12304.021121Ω=×==−−L z Z线路3—4,5—6,7—8的正序阻抗为)(24604.0876543Ω=×===−−−Z Z Z 变压器的等值阻抗为)(1.445.311151005.10100%22Ω=×=×=T T K T S U U Z (注意110kv 是额定电压,而母线电压一般为115kv 高额定5kv 。
115kv 是线电压要折算成相电压,而且要注意单位的统一)2. 距离I 段的整定(1)阻抗整定.)(2.101285.02111Ω=×==−Z K Z rel set 2)动作时间。
s t 01=3. 距离II 段的整定(1)整定阻抗:按下列两个条件选择1)与相邻下一级线路3—4(或5—6或7—8)的保护3(或保护5或保护7)的1段配合)(3.min .ΙΠΠ+=set b AB rel set Z K Z K Z 式中,可取而,85.0=Ιrel K ,8.0=Πrel K )(4.202485.0433.Ω=×==−ΙΙZ K Z rel set 分支系数的计算:设B 母线上的电压为U 。
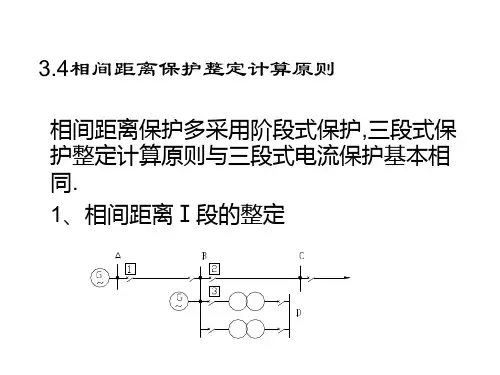

20距离保护的整定计算实例仅供学习与交流,如有侵权请联系网站删除 谢谢2例3-1 在图3—48所示网络中,各线路均装有距离保护,试对其中保护1的相间短路保护Ⅰ、Ⅱ、Ⅲ段进行整定计算。
已知线路AB 的最大负荷电流350max L =⋅I A,功率因数9.0cos =ϕ,各线路每公里阻抗Ω=4.01Z /km ,阻抗角 70k =ϕ,电动机的自起动系数1ss =K ,正常时母线最低工作电压min MA ⋅U 取等于110(9.0N N =U U kV )。
图3—48 网络接线图解: 1.有关各元件阻抗值的计算AB 线路的正序阻抗 Ω=⨯==12304.0L 1AB AB Z ZBC 线路的正序阻抗 Ω=⨯==24604.0L 1BC BC Z Z变压器的等值阻抗 Ω=⨯=⋅=1.445.311151005.10100%2T 2T k T S U U Z 2.距离Ⅰ段的整定(1)动作阻抗: Ω=⨯==2.101285.0rel 1.AB op Z K Z ⅠⅠ(2)动作时间:01=Ⅰt s3.距离Ⅱ段(1)动作阻抗:按下列两个条件选择。
1)与相邻线路BC 的保护3(或保护5)的Ⅰ段配合仅供学习与交流,如有侵权请联系网站删除 谢谢3)(min b rel rel 1.op BC AB Z K K Z K Z ⋅+=ⅠⅡⅡ式中,取8.0,85.0rel rel ==ⅡⅠK K , min b ⋅K 为保护3的Ⅰ段末端发生短路时对保护1而言的图3-49 整定距离Ⅱ段时求min .jz K 的等值电路最小分支系数,如图3-49所示,当保护3的Ⅰ段末端1d 点短路时, 分支系数计算式为215.112)15.01(B A B B A 12b ⨯⎪⎪⎭⎫ ⎝⎛++=+⨯++==X Z X Z Z X X Z X I I K AB BC BC AB 为了得出最小的分支系数min b ⋅K ,上式中A X 应取可能最小值,即A X 最小,而B X 应取最大可能值,而相邻双回线路应投入,因而19.1215.11301220min .b =⋅⎪⎭⎫ ⎝⎛++=K 于是Ω=⨯⨯+=''02.29)2485.019.112(8.01.dzZ 2)按躲开相邻变压器低压侧出口2d 点短路整定(在此认为变压器装有可保护变压器全部的差动保护,此原则为与该快速差动保护相配合),)(T min .b rel 1.op Z K Z K Z AB ⋅+=ⅡⅡ仅供学习与交流,如有侵权请联系网站删除 谢谢4此处分支系数min b ⋅K 为在相邻变压器出口2k 点短路时对保护1的最小分支系数,由图3-53可见Ω=⨯+==++=++==⋅3.72)1.4407.212(7.007.2130122011.op max .B min .A 13min b ⅡZ X Z X I I K AB此处取7.0rel =ⅡK 。

距离保护整定计算现以图2所示多电源电网为例,说明三段式距离保护1的整定计算方法。
和方向电流保护一样,保护1、3、5为一组2、4、6为另一组,由于各自具有方向性,故只需在同一组保护间进行配合。
图2三段式距离保护整定计算说明图(a)网络图例;(b)时限特性保护动作阻抗Z act(一次动作阻抗)的整定计算1.距离I段为了保证选择性,保护1瞬时动作的距离I段动作阻抗应按躲过相邻下一元件首端(图2中的K1、K2点)短路的条件选择,即Z act.1Ⅰ.=K rel Z1L AB式中K rel—可靠系数,一般取0.8~0.85;Z1--线路每公里的正序阻抗。
按式Z act.1Ⅰ.=K rel Z1L AB整定的距离I段,不管系统运行方式如何变化,其保护范围不变,即保护线路全长的80%一85%,这是电流速断保护无法比拟的,2、距离Ⅱ段(1)保护1距离Ⅱ段应与相邻线路BC的距离I段的保护范围相配合,并引人分支系数,考虑助增(或汲出)电流对保护1距离Ⅱ段测量阻抗的影响,即Z act.1Ⅱ=K rel.(Z1L AB+K bar.BC Z act.3Ⅰ)式中Z act.3Ⅰ一相邻线路保护3距离1段的动作阻抗:K bar.BC—考虑助增(或线路BC汲出)电流对保护1而言的分支系数,应取可能的最小值K rel—可靠系数,一般取0.8.(2)对于图2(a)所示网络,因与线路AB相邻的还有降压变压器T,故保护1的距离Ⅱ段还应躲过线路末端降压变压器低压侧母线上(图2,a中的K3点)的短路,即Z act.1Ⅱ=K rel.T.(Z1L AB+K bar.T Z T.MIN)式中Z T.MIN-变压器的最小等值阻抗:K bar.T考虑助增(或变压器汲出)电流对保护1而言的分支系数;K rel.T—与变压器配合的可靠系数,考虑到Z T.MIN有较大偏差,故取K rel.T≈0.7.按式1和式2算出两个结果,取其中较小者作为Z act.1Ⅱ的整定值,此时t1Ⅱ=t3Ⅰ+△t=0.5s保护1距离Ⅱ段应按被保护线路AB末端短路校验灵敏系数,即Ksen=Z act.1Ⅱ/Z1L AB>1.3-1.5若灵敏系数不满足要求,可改为与保护3的Ⅱ段配合,即Z act.1Ⅱ=K rel.(Z1L AB+K bar.BC Z act.3Ⅰ)相应的t1Ⅱ=t3Ⅰ+△t3.距离Ⅲ段若采用阻抗继电器作为距离Ⅲ段的测量元件时,则动作阻抗应按躲过最小负荷阻抗整定,以保证正常运行情况下距离Ⅲ段不误动作,即Z act.1Ⅲ=Z L.min/K rel K r K ast式中K rel可靠系数,取1.2-1,3:K r返回系数,取1.15-1.25K ast-考虑电动机自起动时使电流增大、电压降低的自起动系数;Z L.min未考虑电动机自起动影响的最小负荷阻抗,其值可按下式计算Z L.min =0.9U rat.ph/I L.max 式中U rat.ph一电网的额定相电压:I L.max未考虑电动机自起动的最大负荷电流,。
高压输电线路距离保护的保护配置及其整定计算本文主要推导和解释了接地距离的保障与相互挨着的线路接地的间距、纵联和零序之间保护相互配合的计算公式。
最重要的是详尽推算了有零序耦合线路互相配合的准确计算方法与计算公式,并且推陈出新应用了综合帮助增长系数的新概念。
标签:接地距离保护;整定计算;输电线路;零序互感1.引言电力系统中的输电线路装配着各种类型的保护装置,然而其保护措施大多数都没有配备接地距离保护。
所以一定解决好接地间距与接地间距的保护、接地间距和零序电流得保护配合等。
因而接地间距的保护核定计算已经升级成为重要的环节之一。
2 接地间距I段整定核定规程部分中规定,接地间距I段核定开本线的后端接地短路故障核定。
但是当被核定得线路和其他得线路有互感耦合的期间,就必须把它的影响考虑进去,必须保证接地间距I段不能越界的错误动作。
2.1 正常运行的零序互感线路图1所示是一组有零序互感的双端共端线路。
经过分析可得:双回双端共端电线后端接地出现故障时,如果不把互感核定零序补偿系数考虑在内,繼电器阻抗的反映会超过实际阻抗,保护线路的灵敏系数会降低。
图1 双端共端零序互感线路2.2 双回线当中的一回挂地线路的检修当一回挂地线检测维修时,如果没有把互感核定零序补偿系数作为考虑,实际线路所拥有的阻抗大于继电器阻抗。
这样,能使保护的灵敏性提高,但有超越错误的可能。
3. 相邻线路与接地距离保护配合3.1 接地线间距保护Ⅱ段与相邻电线接地间距保护Ⅰ段配合接地间距保护段和接地间距保护段配合实际上上应该根据规程1的某指令运行,规程中式(2)~(5)应该就是相邻线接地间距保护的Ⅰ段保护的相互合作,具体推算见下:如图2所示,开关A核定的阻抗为:图2 接地距离保护Ⅱ段与相邻线接地距离保护Ⅰ段配合由以上计算结果,式(1)乘上可靠系数Kk和核定规程[1]中的式(1)完全相同。
规程中的式(4)是规定程序中式(1)的简化算法。
用规程中的式(4)计算既复杂又不准确,人为地使Ⅱ段保护区间大大的缩短,大概会使保护配合更加困难,甚至不能满足配合要求。
• 17•输电线路距离保护对于整个电力系统的稳定运行以及被保护的电气设备都是重要的,同时选择合适的整定计算系统,对电力系统继电保护装置的可靠运行具有十分重要的作用。
本论文主要是针对输电线路距离保护的形式、发展现状进行分析,并对其整定计算的系统和核心内容进行总结,并提出了展望。
随着国民经济的飞速发展,电网越来越庞大,其复杂的架构也是我们研究的难题。
高压的输电线路可能出现的故障情况也就越来越多。
在这种情况下,在线路距离保护技术方面,要解决以下几个问题:第一,要准确地辨别出问题的线路,并且快速地将它们移除,最大化的缩小停电范围;第二,要能非常好的调整线路状态以应对环境的改变,并且保持其稳定的特性;第三,巡检人员可以方便地检查,维修。
输电线路距离保护整定计算必须满足“四性”的要求。
即“可靠性”、“选择性”、“快速性”和“灵敏性”。
对高压电网输电线路进行整定计算,为了满足上述要求,装设的距离保护装置要合理选择和配合,这些工作都是不容易的。
1 距离保护研究现状单纯的电压保护以及电流保护,他们所被保护的范围受系统运行方式、途径变化的影响比较大,在某些特定的运行方式下,快速断开的保护的被保护区域很小,甚至没有可以被保护的区域。
对于很大的位移值、有着很多负载的线路采用超过电流值的保护往往不能满足系统能否反应故障的要求。
为此,我们就必须采用功能性更好的保护装置,而距离保护就是顺势而生的一种保护原理。
距离保护是利用短路时电压、电流在同一时间发生变化的特征,测量计算出U 与I 的比值,反应发生故障的位置到保护架设处的距离,并根据该数值的大小而确定动作时间的一种保护装置。
距离保护原理根据数据处理方式的不同可分为频域距离保护和时域距离保护。
1.1 频域距离保护侯俊杰、樊艳芳、王一波等人介绍了频域距离保护利用工频量计算测量阻抗。
但风电、光伏发电等新能源接入系统时其不同于传统电网输电线路的故障特性,使得频域距离保护可靠性受到影响,保护可能无法正确动作。
k距离Ⅰ段的整定按躲过本线路末端短路时的测量阻抗来整定ABI set1Z Z其中 850~8t 定值:时间:距离Ⅱ段的整定相邻线路故障时,本线路的测量阻抗1I U A=U B U AB =:分支系数(和电流保护中定义相同)。
max 的计算方法同前。
b.min set1ZK=与相邻线路段配合。
与相邻变压器快速保护配合。
b.min ZK=K 取上述最小值作为整定阻抗。
距离Ⅱ段的整定灵敏度校验要求 ≥若灵敏度不满足要求,改为与相邻元件的保护故障点选取本线路末端。
senKII 距离Ⅱ段的整定距离Ⅱ段的整定动作时间比与之配合的相邻元件保护动作时间长△+∆+∆取较大的时间做为本保护动作时间。
与相邻下级线路距离保护段或min AB III set1Z Z+与相邻下级变压器的电流、电压保护配合(min AB Z Z+距离Ⅲ段的整定(1)定值计算变压器的电流、电压保护的最小保护范围。
(1)定值计算按躲过最小负荷阻抗整定。
考虑外部故障切除后,电动机自启动时,应可靠返回。
最小负荷阻抗:ss L K Z )=ϕmaxN L U I U =返回阻抗:relre L Z =ϕ动作阻抗:距离Ⅲ段的整定)灵敏度校验:近后备: 远后备:ABIII set1Z Z要求BCmax set1Z =要求故障点取本线路末端k1k1k2故障点取相邻线路末端k2)动作时间:应比与之配合的相邻设备保护动作时间大一个时间级差Δ考虑躲振荡,一般应大于1.5~2s。
与多条相邻线路保护配合时,取最大时间做为动作时间。
(2) 距离 I 段的整定(i) 整定阻抗)(..Ω=⨯==-2101285021I relI setZ K Z(ii) 动作时间s0I=t(3) 距离 II 段的整定(i) 整定阻抗)(min .I set.3b 21II rel II setZK Z K Z+=-①与保护3(或保护5)的 I 段配合)(..Ω=⨯==-4202485043I relI set.3Z K Z而(3) 距离 II 段的整定(i) 整定阻抗)(min .I set.3b 21II rel II setZK Z K Z+=-①与保护3(或保护5)的 I 段配合)(..Ω=⨯==-4202485043I relI set.3Z K Z 而代入得)()..(.Ω=⨯+⨯=294201911280II setZ3.4.5 对距离保护的评价(1)受运行方式变化影响小,保护区相对稳定,能够在多电源网络中应用,可以保证选择性,其中Ⅰ段完全不受运行方式变化影响。
距离保护的整定计算一、距离保护第一段 1.动作阻抗(1)对输电线路,按躲过本线路末端短路来整定,即取AB K dzZ k Z '='⋅12.动作时限0≈'t 秒。
二、距离保护第二段1.动作阻抗(1)与下一线路的第一段保护范围配合,并用分支系数考虑助增及外汲电流对测量阻抗的影响,即()BC k fz AB k dzZ K K Z K Z '+''=''⋅1式中fz K 为分支系数min ⎪⎪⎭⎫ ⎝⎛=ABBCfz II K(2)与相邻变压器的快速保护相配合()B fz AB k dzZ K Z K Z +''=''⋅1取(1)、(2)计算结果中的小者作为1⋅''dzZ 。
2. 动作时限保护第Ⅱ段的动作时限,应比下一线路保护第Ⅰ段的动作时限大一个时限阶段,即12CABA '图3-50 电力系统接线图AZ 'BABZ BCZ Z 'Z ''Z '''00.5tZ 'Z ''Z '''00.5t3AZ 12CABA '图3-50 电力系统接线图AZ 'BABZ BCZ Z 'Z ''Z '''00.5tZ 'Z ''Z '''00.5t3AZt t t t ∆≈∆+'=''213.灵敏度校验5.1≥''=ABdzlm Z Z K如灵敏度不能满足要求,可按照与下一线路保护第Ⅱ段相配合的原则选择动作阻抗,即()2.dz fz AB k dzZ K Z K Z ''+''=''这时,第Ⅱ段的动作时限应比下一线路第Ⅱ段的动作时限大一个时限阶段,即t t t ∆+''=''21三、 距离保护的第三段1.动作阻抗按躲开最小负荷阻抗来选择,若第Ⅲ段采用全阻抗继电器,其动作阻抗为min.1.1fh zqh k dzZ K K K Z '''='''式中2.动作时限保护第Ⅲ段的动作时限较相邻与之配合的元件保护的动作时限大一个时限阶段,即t t t ∆+'''='''23.灵敏度校验作近后备保护时5.11.≥'''=⋅ABdzlm Z Z K 近作远后备保护时2.1≥+'''=⋅BCfz ABdzlm Z K Z Z K 远式中,K fz 为分支系数,取最大可能值。
思考:灵敏度不能满足要求时,怎么办?解决方法:采用方向阻抗继电器,以提高灵敏度方向阻抗继电器的动作阻抗的整定原则与全阻抗继电器相同。
考虑到正常运行时,负荷阻抗的阻抗角fh ϕ较小,(约为 25),而短路时,架空线路短路阻抗角d ϕ较大(一般约为 65~85)。
如果选取方向阻抗继电器的最大灵敏角d lm ϕϕ=,则方向阻抗继电器的动作阻抗为()fh d zq h kfh dzK K K Z Z ϕϕ-'''='''cos min.1. 结论:采用方向阻抗继电器时,保护的灵敏度比采用全阻抗继电器时可提高)cos(1fh d ϕϕ-。
四、阻抗继电器的整定保护二次侧动作阻抗jx TVTAdzj dz K n n Z Z =.式中jx K ——接线系数五、对距离保护的评价1.主要优点(1)能满足多电源复杂电网对保护动作选择性的要求。
(2)阻抗继电器是同时反应电压的降低与电流的增大而动作的,因此距离保护较电流保护有较高的灵敏度。
2.主要缺点(1)不能实现全线瞬动。
(2)阻抗继电器本身较复杂,调试比较麻烦,可靠性较低。
例3-1 在图3-52所示网络中,各线路均装有距离保护,试对其中保护1的相间短路保j XRfhZ zdZ d ϕfhϕ图3-51 全阻抗继电器和方向阻抗继电器灵敏度比较1C A 图3-52 网络接线图Z BNM2345678910k m 60k m30m a x.f n I k V 3/1151='E Ω25m a x1=⋅x X Ω20m i n 1=⋅x X k V 3/1152=''E Ω30m a x 2=⋅x X Ω25m i n2=⋅x X M V A 5.31=B S 5.10%=d U s 5.010=''t s 5.08='''t k m60护Ⅰ、Ⅱ、Ⅲ段进行整定计算。
已知线路AB 的最大负荷电流350max =⋅fh I A,功率因数9.0cos =fh ϕ,各线路每公里阻抗Ω=4.01Z /km ,阻抗角 70=l ϕ,电动机的自起动系数1=zq K ,正常时母线最低工作电压m in ⋅fh U 取等于110(9.0=e e U U kV )。
解: 1.有关各元件阻抗值的计算2.距离Ⅰ段的整定 (1)动作阻抗:Ω=⨯='='⋅2.101285.01AB k dzZ K Z(2)动作时间:0='t s3.距离Ⅱ段(1)动作阻抗:按下列两个条件选择。
1)与相邻线路BC 的保护3(或保护5)的Ⅰ段配合)(min 1BC fz AB K dz Z K K Z K Z ⋅⋅'+''='215.112)15.01(2122112⨯⎪⎪⎭⎫ ⎝⎛++=+⨯++==X ABX BC BC X X AB X fz X Z X Z Z X X Z X I I K19.1215.11301220min .=⋅⎪⎭⎫ ⎝⎛++=fz K于是Ω=⨯⨯+=''⋅02.29)2485.019.112(8.01dzZ2)按躲开相邻变压器低压侧出口2d 点短路整定)(min .1B fh K AB k dzZ K K Z K Z ⋅'+''='⋅此处分支系数m in⋅fh K 为在相邻变压器出口2d 点短路时对保护1的最小分支系数,Ω=⨯⨯+==++=++==⋅⋅3.72)1.4407.27.012(7.007.213012201''1max .2min .113min dz x AB x fz Z X Z X I I K取以上两个计算值中较小者为Ⅱ段定值,即取Ω=⋅02.29''1dz Z(2)动作时间s t t t 5.0'3''1=∆+=4.距离Ⅲ段(1) 动作阻抗Ω=⨯⨯=⋅⨯==-'''='''⋅⋅⋅⋅⋅5.16335.031109.031109.0)cos(maxmaxmin min .min1fh fh fh fh fh d zq h k fh dzI I U Z K K K Z Z ϕϕ取8.259.0cos ,70,1,15.1,2.11======='''-fh lm d zq h k K K K ϕϕϕ于是Ω3.165)8.2570cos(115.12.15.163'''1=-⨯⨯⨯=⋅ dz Z(2)动作时间 :t t t t t t ∆+'''=∆+'''='''2310181或取其中较长者 0.25.035.01=⨯+='''t s (3)灵敏性校验1)本线路末端短路时的灵敏系数2)相邻元件末端短路时的灵敏系数 ①相邻线路末端短路时的灵敏系数为BC fz ABdzlm Z K Z Z K max 1⋅⋅⋅+'''=远式中,max⋅fz K 为相邻线路BC 末端3d 点短路时对保护1而言的最大分支系数,其计算等值电路如图3-54所示。
48.225251225min 2min 2max 112max =++=++==⋅⋅⋅⋅x x AB x fz X X Z X I I K②相邻变压器低压侧出口2d 点短路时的灵敏系数中,最大分支系数为48.225251225min 2min 2max 113max =++=++==⋅⋅⋅⋅x x AB x fz Z Z Z Z I I K1I2I 2d 3I BCZ 85.0ABZ ABC图3-54 整定距离Ⅲ段灵敏度校验时求 的等值电路m i n。
f z K BZ D3d min2⋅x X ma x1⋅x X。