工程力学A 参考习题之虚位移原理习题及解答

第11章 虚位移原理——习题1~1711-1 图示平面机构，圆盘的半径为r ，可绕其中心轴转动，直杆BC 和BD 的长度为l 1 = 2r ，直杆AB 的长度为l 2 = 3r ，试建立图示位置圆盘的虚转角θδ与滑块C 的虚位移C r δ之间的关系。

（题11-1答案：）11-2 在图示平面机构中，O 1A = AB = r ，O 2C = 2r ，BD = 4r ，C 为杆BD 的中点，试建立图示位置杆O 1A 的虚转角1δθ与杆O 2C 的虚转角2δθ之间的关系。

（题11-2答案：）11-3 如图所示曲柄摇杆机构，已知OA = OB = l ，试建立图示位置两杆虚转角之间的关系。

（题11-3答案：）11-4 在图示平面机构中，半径为R = 2r 的四分之一细圆环BD ，其上套一套筒A ，套筒与可绕轴O 转动的直杆OA 铰接，OA 的长度为l = 3r ，试建立图示题11-1图题11-2图位置杆OA 的虚转角与点D 的虚位移之间的关系。

（题11-4答案：）11-5 在如图所示平面机构中，O 1A = O 3C = O 3D = AB = l ，在图示位置，CB = O 2B =l 332，试建立该位置A 、D 两点虚位移之间的关系。

（题11-5答案：）11-6 在图示平面机构中，ABD 为边长等于a 的正三角形平板，O 1B 、O 2D 的杆长也均为a 。

机构在图示位置时，杆OE 与水平线成60◦角，A 、D 、O 2在同一水平线上，O 1B 位于铅垂位置，且OA = a ，试求此瞬时刚体O 1B 与OE 的虚转角之间的关系。

题11-3图题11-4图题11-5图题11-6图（题11-6答案：）11-7 在图示平面四连杆机构中，在杆AB 上垂直地作用有三角形分布载荷，其最大集度为q ，在杆OA 的中点作用有水平向左的主动力F ，且F = ql ，若不计各构件自重和各接触处摩擦，为使系统在图示位置平衡，所需施加的作用于杆BC 上的主动力偶矩M 的值。

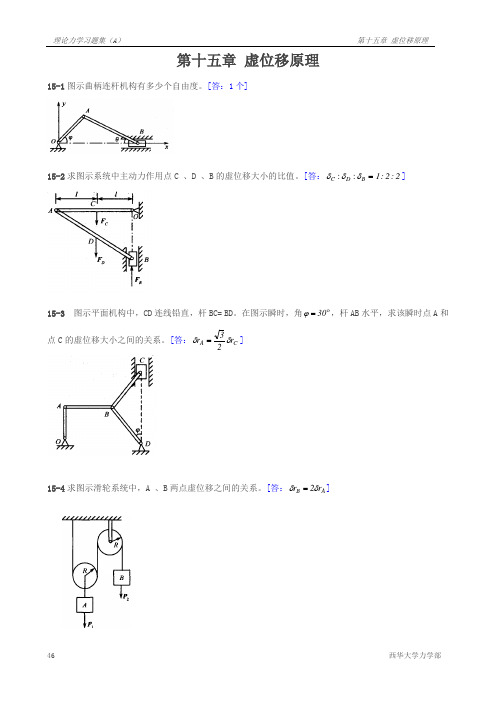
第十五章 虚位移原理15-1图示曲柄连杆机构有多少个自由度。

[答：1个]15-2求图示系统中主动力作用点C 、D 、B 的虚位移大小的比值。

[答：=B D C δδδ::2:2:1]15-3 图示平面机构中，CD 连线铅直，杆BC= BD 。

在图示瞬时，角 30=ϕ，杆AB 水平，求该瞬时点A 和点C 的虚位移大小之间的关系。

[答：C A r 23r δδ=]15-4求图示滑轮系统中，A 、B 两点虚位移之间的关系。

[答：A B r 2r δδ=]15-5重为P 、长为l 的均质杆AB 放置如图。

设各处光滑，在A 点处的水平力F 作用下保持平衡， 60=ϕ，今给A 点一向右的虚位移x δ，试由虚位移原理建立的虚功方程。

[答：0x F -63P=δδ]15-6 杆OA 和AB 各长l ，在A 点用铰链连接，在点O 和B 间连接一根刚度系数为 k 的铅直弹簧，弹簧的原长为0l 。

当在A 点作用铅垂力A F 时，机构处于图所示的平衡位置，且弹簧被拉伸。

如果不计各构件的重量和摩擦，用虚位移原理求机构处于平衡位置时的角度ϕ。

[答：4kl2kl F arcsinA +=ϕ]15-7 如图所示，两等长杆AB 和BC 在点B 用铰链连接。

在杆的点D 和点E 连接水平弹簧，弹簧的刚度系数为k ；从当距离AC a =时，弹簧的拉力等于零。

已知 AB=l , BD=b ，今在点C 作用水平力F 1使系统处于平衡。

若不计构件重量和摩擦，试用虚位移原理求距离AC 的值x 。

[答：21b l kFa x ⎪⎭⎫ ⎝⎛+=]15-8 在图示机构中，已知：力F ，l GC EG DE DC BC AC ======，弹簧的原长为l ，刚度系数为k 。

试用虚位移原理求机构平衡时，力F 与角θ的关系。

[答：()12sin kl 32F -=θ]15-9 平面机构在力F 1和F 2的作用下，在图所示的角度θ位置平衡。

已知1l BD OD ==，2l AD =，如果不计各构件重量和摩擦，试用虚位移原理求F 1 / F 2的比值。

习 题4-1 如图4-19所示，在曲柄式压榨机的销钉B 上作用水平力F ，此力位于平面ABC 内，作用线平分∠ABC 。

设AB =BC ，∠ABC =θ2，各处摩擦及杆重不计，试求物体所受的压力。

图4-190δ)90cos(δδN =--︒=∑C B F s F s F W θ)90cos(δ)902cos(δθθ-︒=︒-C B s s θθsin δ2sin δC B s s = 虚位移原理0δ)90cos(δδN =--︒=∑C B F s F s F W θ 0δsin δN =-C B s F s F θθθθθtan 2)2sin(sin sin δδ2N F F s s F F C B ===4-2 如图4-20所示，在压缩机的手轮上作用一力偶，其矩为M 。

手轮轴的两端各有螺距同为h ，但方向相反的螺纹。

螺纹上各套有一个螺母A 和B ，这两个螺母分别与长为l 的杆相铰接，四杆形成棱形框，如图所示，此棱形框的点D 固定不动，而点C 连接在压缩机的水平压板上。

试求当棱形框的顶角等于2f 时，压缩机对被压物体的压力。

图4-20ϕϕcos δ)290cos(δC A s s =-︒ C A s s δsin δ2=ϕ而 θϕδπ2c o s δP s A =ϕθϕθϕtan δπsin δcos π22δPP s C ==虚位移原理0δδδN =-=∑C F s F M W θ 0tan δπδN =⨯-ϕθθPF M ϕcot πN PMF =4-3 试求图4-21所示各式滑轮在平衡时F 的值，摩擦力及绳索质量不计。

图4-21虚位移原理0δδδ=+-=∑A B F s G s F W(a) A B s s δ2δ= 2G F =(b) A B s s δ8δ= 8G F = (c) A B s s δ6δ= 6G F =(d) A B s s δ5δ= 5G F =4-4 四铰连杆组成如图4-22所示的棱形ABCD ，受力如图，试求平衡时θ应等于多少？图4-22θθcos δ)290cos(δC B s s =-︒ C B s s δsin δ2=θ 虚位移原理0δcos δ2δ=-=∑C B F s G s F W θ0sin δ2cos δ2=⨯-θθB B s G s Fθtan =GF4-5 在图4-23所示机构中，曲柄OA 上作用一力偶矩为M 的力偶，滑块D 上作用一水平力F ，机构尺寸如图。

虚位移原理习题及解答机构在图示位置平衡，不计各杆自重，求力F 1和F 2的关系解：设AB 杆的A 点为动点，OC 杆为动系，A 、C两点的虚位移如图，则：φδδcos A e r r =φδδδcos OAeeC l ar a r r ==由上述各式和虚功方程012=-C A r F r F δδ解出：机构在图示位置平衡，不计各杆自重，求力偶矩M 与F 之间的关系。

解：设OA 杆的虚位移为δφ，则A 、D 、B各点虚位移如图，图中δφδa r A =θδθδcos 2cos A B r r = θδθδcos 2sin D B r r = 0=+-D r F M δδφ θ2tan F M =已知：弹簧原长0.3m ，刚度系数k=5kN/m ，机构在图示位置平衡，不计各杆自重，求力偶矩M 的大小。

解：设CD 杆上D 点为动点，AB 杆为动系，它们的虚位移如图θδδtan e r r r =θδδδθcos 0.3AD e e rr ==由虚功方程 0=-r k r F M δδθ以及弹簧力)]cos 3.06.0(3.0[θ--=k F k可解出 θθθs i n c o s c o s14503-=M N.m已知：BC=AB=L ，BE=BD=b ，弹簧刚度为k ，当x=a 时，弹簧拉力为零，该系统在力F 作用下平衡，杆重不计，求平衡时x=?解：弹簧力如图，其中)(a x l bk F F k k -='=各力作用点横向坐标及其变分为θcos )(b l x D -= θδθδs i n )(b l x D --= θcos )(b l x E +=θδθδs i n )(b l x E +-=θcos 2l x C = θδθδs i n2l x C -= 代入虚功方程0=∑x F xδ0=+'-C E KD K x F x F x F δδδ 解得：22kb Fl a x += 已知：已知均质杆长，杆重皆为P ，滑块C 重P2，滑轨倾角为θ，求平衡时角φ为多大？φsin 2l x D = δφφδ.cos 2l x D = φcos 2l y D = δφφδ.sin 2l y D -=φsin 2lx E = δφφδ.cos 2l x E =φcos 23l y E = δφφδ.sin 23l y E -= 0=C x 0=C x δφcos 2l y C = δφφδ.sin 2l y C -=把它们代入虚功方程 0)(=+∑y F x F y xδδ得：0sin sin cos sin cos 21111=++++C E E D D y P y P x P y P x P θδθδθδθδθδ解得： θφc o t)(2t a n 211P P P +=15-15 用虚位移原理求图示桁架中杆3的内力。