当前位置：文档之家 › 严格平稳随机过程

严格平稳随机过程

  • 格式：ppt
  • 大小：550.50 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

平稳随机过程的概念

平稳随机过程的概念

所以随机相位周期过程是平稳的. 特别, 随机相位 正弦波是平稳的.
例3
考虑随机电报信号 x( t ) I
信号X ( t )由只
取 I或 I
o
I
t
的电流给出 .
这里 P{ X ( t ) I } P{ X ( t ) I } 1 / 2
而正负号在区间 ( t , t )内变化的次数N ( t , t )
2. 广义平稳过程
{ X ( t ), t T }, 如果对任意 定义1 给定二阶矩过程
t,t T :
E[ X ( t )] X
(常数)
E[ X ( t ) X ( t )] RX ( )
则称{ X ( t ), t T }为宽平稳过程, 或广义平稳过程 .
其中A是服从瑞利分布的随机 变量, 其概率密度为
a e f (a ) 2 0,
a2 2 2
, a0 a0
是在(0,2π )上服从均匀分布且与 A 相互独立的 随机变量, 是一常数,问X n ( t ) 是不是平稳过程?
解 因 E ( A)

a
2 2
即相关函数只与k l 有关,
所以它是宽平稳的随机序列.
如果 X1 , X 2 ,, X k ,是独立同分布的 , 则序列是
严平稳的.
例2 设s( t )是一周期为T的函数,是在(0, t )上服
从均匀分布的随机变量 , 称X (t ) s(t )为随机
相位周期过程. 试讨论它的平稳性 .
说明 (1) 严平稳过程只要二阶矩存在, 则它必定也 是宽平稳的. 反之不成立. (2) 宽平稳的正态过程必定也是严平稳的.

平稳随机过程

平稳随机过程
பைடு நூலகம்
e
2
只与 有关.
{X (t ), t 0}是平稳过程.
例4 设{Y(t),t≥0}是正态过程.且 a mY (t ) t, CY (t, t ) e , 其中，，a 0,
令 X (t ) Y (t b) Y (t ), t 0, 其中b 0, 试证明 {X (t ), t 0}是一严平稳过程.
试讨论{X(t),t≥0}的平稳性.
mX (t ) 0 常数.
RX (t, t ) E[ X (t ) X (t )]
P( X (t ) X (t ) 1) P( X (t ) X (t ) 1)
P( X (t ) X (t ) 1) P( X (t ) X (t ) 1)
n
由于 mX (tk ) mX mX (tk )
RX (tk , tl ) RX (tl tk ) RX (tk , tl ) k , l 1, 2,, n
(t1 , t2 ,, tn ; u1, u2 ,, un )
例1 设S(t)是周期为T的可积函数.令X(t)=S(t+Θ) t∈(-∞,+ ∞), Θ～U[0,T].称{X(t), -∞<t<+ ∞} 为随机相位周期过程,试讨论它的平稳性.
mX (t ) E[X(t)]

T 0
1 t T s( )d 为常数 T t
1 T R（t , t ) s(t )s(t )d X T 0 1 t T s( )s( )d 只与 有关系. T t 它是平稳过程
由于mX (t ) E[ X (t )] E[W (t a) W (t )] 0, t 0

第十二章-平稳随机过程

第十二章-平稳随机过程
7
若T为离散集, 称平稳过程{X(t), t T }为 平稳序列.
广义平稳过程
严平稳过程
严平稳过程 二阶矩存在 广义平稳过程
严平稳过程 正态过程 广义平稳过程
8
例1 设{Xk , k = 1,2,…}是互不相关的随机变量 序列, E[Xk ] = 0, E[Xk ²] = σ², 则有
解 由假设, Θ的概率密度为
f
(
)
1
/
T, 0,
0 T,
其 它.
于是, X(t)的均值函数为
T
E[ X (t)] E[s(t )]
0
s(
t
)
1 T
d
1
t T
s( )d
Tt
10
利用s(φ)的周期性, 可知
E[X (t)] 1 T s( )d 常数. T0
而自相关函数
RX (t, t ) E[s(t )s(t )]
• 当X(t)和Y(t)是联合平稳随机过程时, W(t) = X(t) +Y(t)是平稳随机过程.
18
事实上, E[W(t)]= E[X(t)] + E[Y(t)] = 常数.
E[W (t)W (t )] E{[X (t) Y (t)][X (t ) Y (t )]} E[ X (t)X (t ) X (t)Y (t ) Y (t)X (t ) Y (t)Y (t )] E[ X (t)X (t )] E[ X (t)Y (t )] E[Y (t)X (t )] E[Y (t)Y (t )] RX ( ) RXY ( ) RYX ( ) RY ( ) RW ( )
t1, t2,, tnT, t1+h, t2 +h,,tn+h T， 若(X(t1), X(t2),, X(tn))与

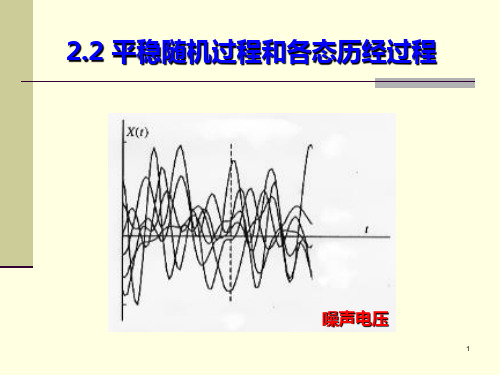
2.2 平稳随机过程和各态历经过程

2.2 平稳随机过程和各态历经过程
P59图2.6
(d ) : E[ X (t )] E[ A cos(t )]
E[ A] E[cos(t )]
X (t ) A cos(t )
cos( ) cos cos sin sin
E[cos(t ) cos sin(t ) sin ]
f X ( x, t ) f X ( x, t ) 令 t , 则有 : f X ( x, t ) f X ( x,0) f X ( x)
a[sin(0T ) sin( 0T )] lim 0 T 2T0
E[ X值具有各态历经性 .
17
1 T X (t ) X (t ) lim T X (t ) X (t )dt T 2T 1 T lim T a cos(0t ) a cos(0t 0 )dt T 2T a2 T lim T cos(0t ) cos(0t 0 )dt T 2T T a2 T lim [ cos(20t 0 2 )dt cos(0 )dt] T T T 4T a2 a2 lim 2T cos(0 ) cos(0 ) RX ( ) T 4T 2
平稳过程X (t )和Y (t )的互相关函数具有联合 各态 历经性的充要条件与上 式相似, 只是将相应的自 相关函数改为互相关函 数即可.
4、 对于均值为零的平稳高 斯过程X (t ), 若自相关函数 连续, 各态历经的充要条件是 :


0
RX ( ) d
21
严平稳过程X(t)的一维概率密度与时间无关
2
2.2.1 严平稳过程
如果对于任意的 , 随机过程X (t )的任意n维概率密度满足 f X ( x1 , x2 ,, xn ; t1 , t2 ,, tn ) f X ( x1 , x2 ,, xn ; t1 , t2 ,, tn ) 则称X (t )为严平稳过程 .

第五讲平稳随机过程与各态历经过程

第五讲平稳随机过程与各态历经过程

第五讲 平稳随机过程与各态历经过程5．1 平稳随机过程在通信与信息领域，很多随机过程都是平稳的或近似平稳的，这是最简单的一类随机过程。

观察随机过程：)cos()(Φ+Ω=t A t X ：)cos()(Φ+=t a t X ω： )cos()(ϕω+=t A t X ： )cos()(ϕ+Ω=t a t X ：当（a）（d）中的Φ服从某种分布时，它们的数学期望和方差很可能2,0[π均匀分布不随时间而改变（平稳的概念）；当（a）中的Φ服从]时，任何一个样本都可代表这个过程（各态历经的概念）。

5.1.1严平稳过程性质：5.1.2宽（广义）平稳过程例题：3.1.3 各态历经过程例题：例2：5.2 平稳随机过程相关性分析5.2.1 自相关函数的性质性质1 实平稳过程X(t)的自相关函数是偶函数，即 )()(ττ-=X X R R 同样可得 )()(ττ-=X X C C性质2 平稳过程的均方值就是自相关函数在0=τ时的非负值0)]([)0(2≥=t X E R X性质3 平稳过程X(t)自相关函数的最大值在0=τ处 )()0(τX X R R ≥ 同理可证 )()0(τX X C C ≥性质4 周期平稳过程X(t)的自相关函数是周期函数，且与周期平稳过程的周期相同 )()(ττX X R T R =+注：若平稳过程X(t)满足X(t)=X(t+T)，则称它为周期平稳过程，其中T 为过程的周期。

性质5 非周期平稳过程X(t)的自相关函数满足)()0()()(lim 22∞-==∞=∞→X X X XX X R R m R R σττ从上面的讨论看出，对于一个平稳随机过程，自相关函数是它的最重要的数字特征，由它可得到其它的数字特征：数学期望 )(∞±=X X R m 均方值 )0()]([2X R t X E = 方差 )()0(2∞-=X X X R R σ 协方差 )()()(∞-=X X X R R C ττ例：已知非周期平稳随机过程X(t)的自相关函数为231916)(ττ++=X R求：X(t)的均值和方差。

概率论第三章 平稳随机过程

概率论第三章 平稳随机过程
则称X(t)为宽平稳过程(或称广义平稳过程)
严平稳过程只要均方值有界， 就是广义平稳的， 但反之则不一定。
当我们同时考虑两个平稳过程X(t)和Y(t)时，若它 们的互相关函数仅是单变量τ 的函数，即
RX Y (t1, t2 ) E[ X (t1 )Y (t2 )] RXY ( ), t2 t1,
则称X(t)和Y(t)宽平稳相依，或称这两个随机过程 是联合宽平稳的。
例3.1 设随机过程 X (t) a cos(0 t )
式中a，ω0为常数，Φ是在区间(0，2π)上均匀分 布的随机变量, 这种信号通常称为随相正弦波。求 证X(t)是宽平稳的。
二、各态历经（遍历）随机过程
在上面的讨论中，每当谈到随机过程时，就意味 着所涉及的是大量的样本函数的集合。要得到随机过 程的统计特性，就需要观察大量的样本函数。
ln
p( X
/
mX
)
K
N 1
exp
i0
(xi
mX
2
2 X
)2
均值估计
让对数似然函数取最大值
ln p( X / mX ) 0 m X
得到均值的最大似然估值
mˆ X
1 N
N 1
xi
i0
此式说明，可用N个观测值的算术平均作为均值mX的估值。
估计量的性质（工程）
1．有偏估计与无偏估计
由于估计量依赖于观测结果，因此估计量本身是 随机变量，于是它也存在其均值和方差。
定义1：取对应于ρX(τ)=0．05的那个时间为相关 时间τ
0
定义2：用图3.6中的矩形(高为ρX(0)=1，底为τ0的
矩形)面积等于阴影面(ρX(τ)积分的一半)来定义
τ0，即

2平稳随机过程

平稳随机过程
一、定义回顾
1. 严、宽平稳随机过程(后者为主)
2. 数字特征。（二阶矩条件， x ，Rx()， Rx(m) ）
例 1. 设状态连续、时间离散的随机过程，
X n s2 inn , n 1 ,2 ,
其中 ~U(0,1) 是随机变量。讨论序列的平稳性。
解. 首先验证是否为二阶矩过程。然后考虑
E[W(t)W(t+)]=E{[X(t)+Y(t)][X(t+)+Y(t+)]} =E[X(t)X(t+)]+E[X(t)Y(t+)]+E[Y(t)X(t+)]+E[Y(t)Y(t+)] =Rx()+RxY()+RxY(-)+RY()
可见W(t)的自相关函数Rw(t,t+)只依赖于,所以 w(t)为平稳过程.
E(Xn)01si2 nndxx0
RX (n, n m) E( X n X nm )
1
0 sin 2nx sin 2 (n m)xdx
1
1
[cos 2mx cos2 (2n m)x]dx
20
1
/ 2, m 0 0, m 0
,
只依赖于m，所以是平稳序列。
例 2. 设随机过程，
不依赖于t？
依赖与Y的方差是否为零。
E [Y2]0 P (Y0)1 ,
与题设矛盾，故非平稳。
二、自相关函数的性质（平稳）
性质1. Rx(0)0； 证: Rx(0)=E[X2(t)]0
性质2. Rx()为偶函数，即Rx(-)=Rx() 证： Rx(-)=E[X(t)X(t-)]= E[X(t-)X(t)]= Rx()

随机过程第六章


2 X
mx2
若随机过程X(t)平稳，则其均值、均方值和方差均为常数。
对于严平稳随机过程X(t)的二维分布F2(X1,X2;t1,t2)=F2(X1,X2;t1+ ε,t2+ ε)， 若令ε=-t1，则
F2(X1,X2;t1,t2)=F2(X1,X2;0,t2-t1)，令t2-t1= τ ，则 F2(X1,X2;t1,t2)=F2(X1,X2; τ)
1.
l.i.mcn
lim
n
cn
c
2. l.i.mU U
3. l.i.m(cnU ) cU
4. l.i.m(aX n bYn ) aX bY
5.
lim
n
E[
X
n
]
E[ X
]
E[l.i.mXn
]
6.
lim
n,m
E[
X
nYm
]
E[
XY
]
E[(l.i.mX
n
)(l.i.mYm
)]
定理6.2
设{Xn}为二阶矩随机序列，则{Xn}均方收敛的充要条件为下列极限存在：
各态历经定理的意义：
一个实平稳过程，如果它是各态历经的，则可用任意一个样本函数的
时间平均代替过程的集合平均，即
mX
l.i.m 1 T T
T
x(t)dt,
0
RX
(t)
l.i.m
T
1 T
T
x(t)x(t )dt
0
若样本函数X(t)只在有限区间[0,T]上给出，则对于实平稳过程有下列估
计式
l.i.m 1
T 2T
T
T X (t) X (t ) dt RX ( )

2-2 平稳随机过程和各态历经过程


18
1 lim T →∞ T
∫
2T
0
(1 −
τ1
2T
)[ B (τ 1 ) − R 2 (τ )]d τ 1 = 0 X
证：
E < X (t ) >= E [
l .i . m T →∞
1 2T
∫
T
−T
X (t ) dt ] =
l .i . m T →∞
1 2T
∫
T
−T
E [ X (t )]dt
=
l .i . m T →0
13
例题
的时间平均为： 解： X(t)的时间平均为： 的时间平均为
1 T /2 X (t ) = lim ∫ A cos(ωc t + θ )dt = 0 −T / 2 T →∞ T
X(t)的时间相关函数： 的时间相关函数： 的时间相关函数
1 T /2 R (τ ) = lim ∫ A cos(ω c t + θ ) ⋅ A cos[ω c (t + τ ) + θ ]dt −T / 2 T →∞ T T /2 A2 T / 2 = lim ∫−T / 2 cos ω cτ dt + ∫−T / 2 cos( 2ω c t + ω cτ + 2θ ) dt T → ∞ 2T
∀∈ f X ( x1, x2 ; t1, t2 ) = f X ( x1, x2 ; t1 + λ, t2 + λ)
令λ =−t 1 → f X ( x1x2;0, t 2 − t1) = f X ( x1, x2;τ )
RX (t1, t2 ) = ∫
∞
−∞ −∞ 1
∫
∞

随机过程第五章 平稳随机过程



1,
0,
T st;
其他.
E{Y (s)Y (t)} E{E[Y (s)Y (t) ]}
st
1 P{ T s t } 1 ,
T 对于 t 的其它情形可做类似推理.
电子科技大学
随机二元传输过程是一个平稳过程,记τ=s－t,
其自相关函数为
0,


),
a;
0,
a
RX(t, t+τ)与 t 无关, 故X(t) 是宽平稳过程.
P128例12 泊松过程不是平稳过程，
是平稳增量过程.
电子科技大学
三、两种平稳性的关系
1）严平稳过程不一定是宽平稳的; 因宽平稳过程一定是二阶矩过程,而严平稳 过程未必是二阶矩过程. 2）宽平稳不一定 严平稳;
CX (s,t) RX (s,t) mX 2 RX () mX 2
电子科技大学
注 自协方差函数与自相关函数都仅依赖于t－s.
平稳过程在实际中是常见过程,如
照明电网中电压的波动过程; 电子系统中的随机噪声; 稳定气象条件下海域中一定点处的海浪高度 随时间的变化或随地点的变化(平稳随机场)； 卫星图片中相同条件下的灰度水平.
t 0,
随机变量与 随机过程》
其中X0 与N(t)相互独立，且
美 A.帕普
力斯，p303
C C
X0 ～ 1 1 C > 0,
2 2
电子科技大学
讨论｛X(t), t≥0｝的平稳性.
C
－C
解 因 X (t) X0(1)N(t) , t 0, mX (t) E[X(t)] E(X0 )E[(1)N(t)] 0, t 0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1. 严格平稳的定义
定义: 随机过程 X(t)的任意N维统计特性与时间起点无关。
（*）
严平稳最基本的特征是时间起点的平移不影响它
的统计特性，即X(t)与X(t+t)具有相同的统计特性。
如果(*)式只对Nk成立，称为k阶严平稳 如果(*)式只对t时成立，称为渐近严平稳
2. 严格平稳过程的性质
如果X(t) 是严格平稳的,则 f X ( x, t ) f X ( x) 与t无关。
如果X(t)是严格平稳随机过程, 则
1 2 , 1 2 1x 2f (1 x2, x 1, t2,(t )dx) dx
()
t1 t2
2. 严格平稳过程的性质
Stationay Gaussian Noise 4
3
2
1
0
-1
-2
-3
-4
0
100 200 300 400 500
Non-stationay Gaussian Noise 4
利用独立性
利用同分布
与n无关
3. 计算举例
例2.3-1：随机幅度信号 X (t ) Y cos 0t
0 是常数 Y ~ N (0,1)
判断X(t)是否严平稳。
由例2.2-1可知：
1
1 x 2
f X ( x, t )
exp
2 cos 0t 2 cos 0t
所以， X(t)不是严平稳的。
2.3 平稳随机过程
严格随机过程 广义平稳随机过程 平稳随机过程自相关函数性质 循环平稳过程 各态历经过程
2.3 平稳随机过程
严格平稳
随
机
K阶严平稳
过
渐近平稳
程
的
广义平稳
平
循环严平稳
稳
性
循环广义平稳
2.3-1 严格平稳随机过程（Strict Wide-Stationary, SSS)
严格平稳的定义 严格平稳过程的性质 计算举例
例2.3-2：随机相位信号 ~U(0,2) 判断X(t)是否严平稳。 解：在例2.2-3中，我们得到了
不难证明， 但X(t)的N维分布很难确定。
本节小结： 严格平稳
统计特性不随时间起点的变化而变化，
性质
f X ( x, t ) f X ( x)均值、方差为常数，
计算举例
3
2
1
0
-1
-2
-3
-4
பைடு நூலகம்
0
100 200 300 400 500
2. 严格平稳过程的性质 可以证明：独立同分布(IID)的随机序列是严格平稳的。 IID: Independent and Identical Distribution 即对于任意的n，X(n)具有相同的一维概率密度，且对 任意n1和n2(n1n2 ), X(n1)和X(n2)相互独立。
二维概率密度
f X ( x1 , x2 , t1 , t2 ) f X ( x1 , x2 , t1 t, t2 t ) f X ( x1 , x2 , t1 t2 , 0) t t2 f X ( x1 , x2 , )
只依赖于，与 t1 和 t2 的具体取值无关。
2. 严格平稳过程的性质