Excel在资金时间价值计算中的应用

EXCEL财务函数在资金时间价值计算中的应用在当今信息时代，数据的收集和信息的处理显得尤为重要。

Excel作为一个应用广泛的电子表格软件被大众所熟知。

其强大的数据分析和处理能力，深受广大用户的喜爱。

Excel既能够帮助用户完成多种要求的数据运算汇总，提取及可视化图表的制作等工作，又帮助用户将复杂的数据转换为有用的信息。

目前大多数企业都引进了各种财务软件，这些软件用于处理基本的财务核算工作和常用财务报表的自动编制工作，而Excel可以在除了常规凭证、账表之外的范围内，可以根据企业自身的特点进行多种有针对性的经营分析与决策。

因此与其他财务软件相比，使用Excel既能高效、正确、灵活的处理会计数据，又能节约成本。

本文以PV函数为例，利用PV函数计算现值，对现有投资方案进行分析与判断。

一·PV函数Pv函数是用来计算一段时间内，连续收到、支出一系列固定金额的现值，或一次性收到、偿还额的现值。

Pv函数的格式为:PV(Rate,Nper,Pmt,Fv,Type)。

其中各参数的含义如下。

Rate:各期的利率、贴现率或投资者期望的最低报酬率。

Nper:付款的总期数或项目投资的使用年限。

Pmt:年金，各期支付的固定金额。

Fv:终值，一次性收到或偿还金额。

投资期终了时，本利和或若干期等额收付款后的本利和。

若不填则视为0。

Type:表示收款或付款日的类型——期初或期末收付款。

1表示每期期初收款或付款，不填或输入0则表示每期期末收款或付款。

二、复利情况下投资方案的选择（一）复利复利是指在整个投资期内，不仅本金要计算利息，本金产生的利息也要计算利息，就是俗称的“利滚利”。

（二）复利现值复利现值是指若干期后一定量资金折现到现在的金额。

其计算公式为：P=公式中P——现值，即本金；F——终值，即n年后的本利和；——复利现值系数，记为(P/F,i,n)。

（三）案例一次性投资300 000元，假设年回报率为4%，等待期限为30年，到期一次性返还800 000元，该投资方案是否可行？若到期一次性返还1 000 000元，该投资方案是否可行？依题意，求现在应存入多少钱实际为所求复利的现值，该现值与投资本金比较后判断投资方案是否可行。

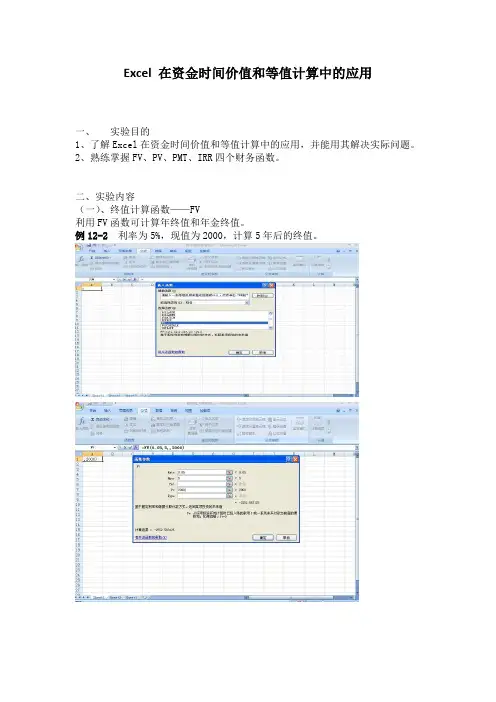
Excel 在资金时间价值和等值计算中的应用一、实验目的1、了解Excel在资金时间价值和等值计算中的应用，并能用其解决实际问题。

2、熟练掌握FV、PV、PMT、IRR四个财务函数。

二、实验内容（一）、终值计算函数——FV利用FV函数可计算年终值和年金终值。

例12-2 利率为5%，现值为2000，计算5年后的终值。

例12-3年利率为5%，年金为400，计算5年后的年金终值。

（二）、现值计算函数——PV利用PV函数可以计算现值和年金现值。

例12-4 利率为5%，终值为2000，计算5年期的现值。

例12-5年利率为5%，年金为400，计算5年期的年金现值。

（三）、偿债基金和资本回收计算函数PMT函数可通过终值和现值分别计算年金值。

例12-6 年利率为5%，终值为2000，计算5年期内的年金值。

例12-7 年利率为5%，现值为2000，计算5年期内的年金值，（四）、NPV函数MPV函数通过使用贴现率以及一系列未来支出（负值）和收入（正值），返回一项投资的净现值。

例12-8 年利率为5%，计算表12-1中现金流量的净现值。

表12-1年份 1 2 3 4 5现金流量-100 50 200 300 350（五）、IRR函数IRR函数返回由数值代表的一组现金流的内部收益率。

这些现金流不必为均衡的，但作为年金，它们必须按固定的间隔产生，如按月或按年。

例12-9 计算12-1中现金流量的内部收益率。

三、实验总结通过本次的上机实验使我再一次认识到Excel 的重要之处，它能帮助我们解决很多现实生活中的繁杂问题，节省了时间，提高了效率。

此次实验中，我们主要学习了FV 、PV 、PMT 、NPV 、IRR 四个财务函数。

掌握FV 函数，能够帮助我们更加轻松快捷地计算年终值和年金终值；掌握PV 函数则可以快速计算现值和年金现值；利用PMT 函数则可通过终值和现值分别计算年金値，例如偿债基金和资金回收等问题；熟练了NPV 函数则可以通过贴现率以及一系列未来支出和收入，反回一项投资的净现值；IRR 函数返回由数值代表的一组现金流的内部收益率。

第3章Excel在资金时间价值计算中的应用 (2)3.1 终值与现值的计算 (2)3.1.1 单利终值与现值 (2)3.1.2 复利终值与现值 (3)3.2 年金的终值与现值 (7)3.2.1 普通年金的终值与现值 (7)3.2.2 先付年金的终值与现值 (12)3.2.3 延期年金的终值与现值 (15)3.3 名义利率与实际利率 (19)3.3.1 Excel实际年利率的计算 (20)3.3.2 Excel名义年利率的计算 (21)3.4 实际应用举例 (22)3.4.1 贷款年利率的计算 (22)3.4.2 贷款偿还期的计算 (23)3.4.3 等额分期付款方式下贷款年偿还额的计算 (24)3.4.4 现金流不规则分布情况下的现值计算 (30)3.5 其他几个资金时间价值的计算函数及其应用 (32)3.5.1 CUMIPMT函数 (33)3.5.2 CUMPRINC函数 (34)3.5.3 FVSCHEDULE函数 (35))1(n i P n i P P F s s s ⋅+⋅=⋅⋅+=第3章 Excel 在资金时间价值计算中的应用3.1 终值与现值的计算终值是指现在的一笔资金按给定的利率计算所得到的未来某一时刻的价值，也称为未来值。

现值是指未来的一笔资金按给定的利率计算所得到的现在时刻的价值。

3.1.1 单利终值与现值单利是指仅对本金计算利息，以前各期产生的利息不再计算利息的利息计算方式。

（1）单利终值假设：P 为现在投入的一笔资金，i s 单利年利率，n 为计息年数，F s 为n 年末的单利终值。

现在投入的一笔资金，n 年末的终值相当于n 年末的本利之和，则：利用Excel 计算单利终值非常简单，只需要在相应的单元格中输入上述计算公式即可。

例如，某人现在存入银行1000元，单利年利率5%，则5年后的本利和为1250元，详见下图：（2）单利现值如果已知一笔现在的存款一定时期后按单利计息的终值，则可求出其等值的现值。

第三讲EXCEL在资金时间价值计算的应用在资金管理和财务决策中，时间价值是一个非常重要的概念。

它指的是钱在不同时间点的价值不同，即在不同时间点上的一定金额的现金流具有不同的价值。

EXCEL是一个非常强大和广泛应用的电子表格软件，它可以帮助我们进行资金时间价值的计算和分析，下面将介绍EXCEL在资金时间价值计算中的应用。

首先，我们可以使用EXCEL的函数来计算一笔未来现金流的现值或未来值。

例如，我们可以使用PV函数来计算一笔未来现金流在当前时点的现值。

在计算时，需要输入一些参数，如未来现金流的金额、折现率（即贴现率）和未来现金流的时间点。

EXCEL可以轻松地计算出未来现金流的现值，并帮助我们做出明智的决策。

其次，我们可以使用EXCEL来计算资金的复利增长。

复利是指投资从一定的本金再投资收益后，下一期的投资收益又会继续以同样的利率投资，使得投资额逐渐增加的过程。

在EXCEL中，可以使用FV函数来计算出资金在未来时点的复利增长额。

同样，需要输入一些参数，如本金、利率和投资期限等。

EXCEL的计算结果可以帮助我们了解资金的增长情况，并作出相应的决策。

此外，EXCEL还可以帮助我们进行不同项目的财务比较和评估。

在资金管理和财务决策中，常常需要比较和评估不同项目或决策对资金时间价值的影响。

通过使用EXCEL的函数和工具，我们可以将不同项目的现金流进行系统地比较和评估。

例如，可以使用IRR函数计算不同项目的内部收益率，并对比选择最佳的项目。

此外，EXCEL还提供了一些工具和图表，帮助我们对资金时间价值进行可视化和分析。

例如，可以使用折线图来显示不同时间点上的现金流量或资金增长情况，从而更直观地比较和分析不同项目的现金流。

可以使用柱状图来显示不同项目的现金流差异，进一步帮助我们做出决策。

总之，EXCEL是一个非常强大和灵活的工具，可以帮助我们进行资金时间价值的计算和分析，从而更好地进行资金管理和财务决策。

通过使用EXCEL的函数、工具和图表，我们可以更直观地理解和比较不同项目的现金流和资金增长情况，以做出更明智的决策。

excel在时间价值中的应用实训报告Excel在时间价值中的应用实训报告时间价值是一种经济学概念，指的是同样数量的资金在不同时间点的价值不同。

因为在不同时间点，资金可以用来进行不同的投资，而不同的投资所能带来的回报率也不同。

因此，在财务决策中，需要考虑时间价值的因素。

在本次实训中，我们将学习如何使用Excel来计算时间价值，并且将其应用于实际的财务决策过程中。

我们需要了解时间价值的两个核心概念：现值和未来值。

现值指的是当前时间点下，一定数量的资金所对应的价值；未来值指的是在未来某个时间点，同样数量的资金所对应的价值。

在Excel中，可以使用PV函数来计算现值，使用FV函数来计算未来值。

这两个函数的参数包括利率、期数、每期支付金额、未来价值等。

其中，利率是指每期所使用的折现率，期数是指资金的投资期限，每期支付金额是指每期需要支付的资金，未来价值是指在投资期限结束后，资金所对应的价值。

假设我们需要在未来5年内投资10万元，并且预计每年可以获得10%的回报率。

那么我们可以使用FV函数来计算在5年后的未来价值：=FV(10%,5,0,-100000)其中，10%是利率，5是期数，0是每期支付金额，-100000是现值。

计算结果为161,051.00元，即在5年后，我们的投资将会增值到161,051.00元。

但是，在实际中，我们需要考虑到资金的时间价值。

也就是说，同样的10万元，在未来5年内的价值将会因为时间的推移而降低。

因此，我们需要将未来的现值折算到当前时间点，以便进行比较和决策。

在Excel中，可以使用PV函数来计算未来价值的现值。

假设我们需要在未来5年内获得161,051.00元的回报，我们可以使用PV函数来计算当前时间点下的现值：=PV(10%,5,0,-161051)其中，10%是利率，5是期数，0是每期支付金额，-161051是未来价值。

计算结果为100,000.00元，即我们在当前时间点下需要投资100,000.00元，才能够在未来5年内获得161,051.00元的回报。