R语言arima模型时间序列分析报告(附代码数据)

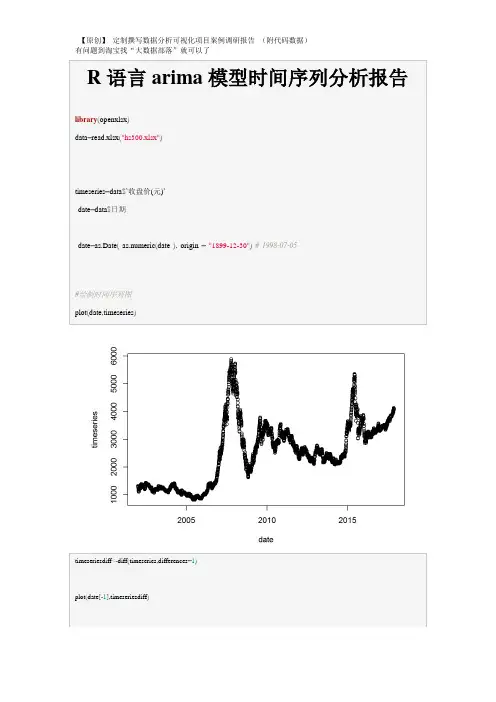
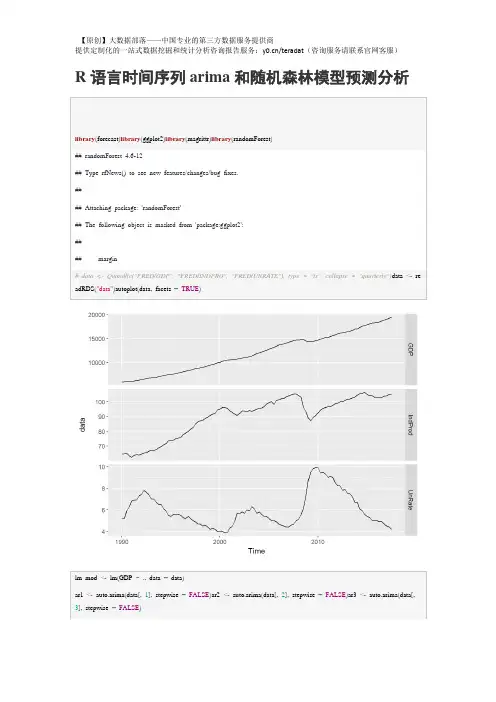
r语言时间序列预测代码一、引言R语言是一种广泛使用的统计软件，在做时间序列预测中有着非常重要的作用。

本文将介绍其在时间序列预测中的基本原理和应用例子，并提供R语言时间序列预测代码。

二、R语言时间序列预测原理时间序列预测就是根据历史数据预测未来数据发展的趋势。

它有三种主要的类型：趋势分析、季节性分析和平稳性分析。

趋势分析就是预测从过去到将来的趋势变化。

季节性分析就是预测一些带有明显季节性变动的变量，例如气温变化，季节性分析可以用来减少预测中的不确定性并预测出可能出现的短期变化。

平稳性分析就是预测在某一时间点之后，变量会围绕某一水平进行摆动的变化，这就是ARIMA模型。

R语言有三种常用的时间序列预测模型：ARIMA模型、自回归模型和移动平均模型。

三、R语言时间序列预测示例下面的示例使用R语言的ARIMA模型来预测一个出行指数的变化： # 导入模块library(forecast)# 读取数据data <- read.csv('travel_index.csv')# 将数据转换成时间序列data_ts <- ts(data, frequency =12,start=c(2015,1),end=c(2020,10))# 训练模型arima_model <- auto.arima(data_ts)# 预测forecast <- forecast(arima_model, h = 24)# 结果可视化plot(forecast)四、结论本文介绍了R语言在时间序列预测中的基本原理和应用，并提供了一个实例的R语言时间序列预测代码。

R语言在时间序列预测中有着广泛的应用，使用起来很方便，可以快速得到准确结果。

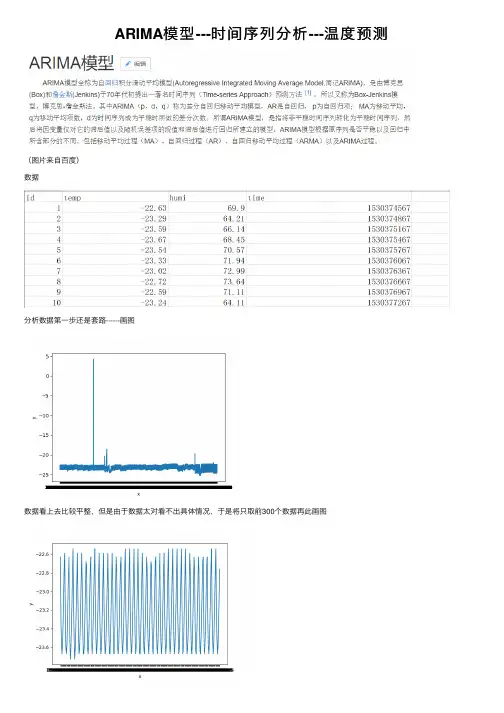
ARIMA模型---时间序列分析---温度预测（图⽚来⾃百度）数据分析数据第⼀步还是套路------画图数据看上去⽐较平整，但是由于数据太对看不出具体情况，于是将只取前300个数据再此画图这数据看上去很不错，感觉有隐藏周期的意思代码#coding:utf-8import csvimport matplotlib.pyplot as pltdef read_csv_data(aim_list_1, aim_list_2, file_name):i = 0csv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[1]))aim_list_2.append(data[3])returndef plot_picture(x, y):plt.xlabel('x')plt.ylabel('y')plt.plot(x, y)plt.show()returnif__name__ == '__main__':temp = []tim = []file_name = 'C:/Users/lichaoxing/Desktop/testdata.csv'read_csv_data(temp, tim, file_name)plot_picture(tim[:300], temp[:300])使⽤ARIMA模型（ARMA）第⼀步观察数据是否是平稳序列，通过上图可以看出是平稳的如果不平稳，则需要进⾏预处理，⽅法有对数变换差分对于平稳的时间序列可以直接使⽤ARMA(p, q)模型进⾏拟合ARMA (p, q) : AR(p) + MA(q)此时参数p和q的确定可以通过观察ACF和PACF图来确定通过观察PACF图可以看出，阶数为9也就是p=9，这⾥ACF图看出⾃相关呈现震荡下降收敛，但是怎么决定出q，我没太明⽩，这⾥姑且拍脑袋才⼀个吧就q=3但是这⾥我遇到了⼀个问题，没有搞懂，就是平稳的序列，如果我进⾏⼀阶差分后应该仍然是平稳的序列，但是这个时候我⼜画了⼀个ACF 与PACF图，竟然是下图这样，lag的范围是-0.04到0.04（不懂）lag的范围是-0.04到0.04的问题原因（修改于再次使⽤此模型）原因：当时，我使⽤的是⼀阶差分，也就是让数据的后⼀个值减去前⼀个值得到新的值，这样就会导致第⼀个值变为缺失值（下⾯的数据是再此使⽤此模型时的数据，与原博客数据⽆关）就是因为此处的值为缺失值，导致绘制ACF与PACF时数据有问题⽽⽆法成功显⽰解决办法，在绘制上述图形前，将第⼀个数据去除：dta= dta.diff(1)dta = dta.truncate(before= ym[1])#删除第⼀个缺失值其实还有就是使⽤ADF检验，得到的结果如图，这个p值很⼩===》平稳画图代码def acf_pacf(temp, tim):x = timy = tempdta = pd.Series(y, index = pd.to_datetime(x))fig = plt.figure(figsize=(9,6))ax1 = fig.add_subplot(211)fig = sm.graphics.tsa.plot_acf(dta,lags=50,ax=ax1)ax2 = fig.add_subplot(212)fig = sm.graphics.tsa.plot_pacf(dta,lags=50,ax=ax2)show()ADF检验代码def test_stationarity(timeseries):dftest = adfuller(timeseries, autolag='AIC')return dftest[1]这⾥先使⽤ARMA(9,3)来实验测试⼀下效果，取前300个数据中的前250个作为train，后⾯的作为test 效果可以说这个模型是真的强⼤，预测的还是⼗分准确的代码def test_300(temp, tim):x = tim[0:300]y = temp[0:300]dta = pd.Series(y[0:249], index = pd.to_datetime(x[0:249]))fig = plt.figure(figsize=(9,6))ax1 = fig.add_subplot(211)fig = sm.graphics.tsa.plot_acf(dta,lags=30,ax=ax1)ax2 = fig.add_subplot(212)fig = sm.graphics.tsa.plot_pacf(dta,lags=30,ax=ax2)arma_mod = sm.tsa.ARMA(dta, (9, 3)).fit(disp = 0)predict_sunspots = arma_mod.predict(x[200], x[299], dynamic=True)fig, ax = plt.subplots(figsize=(9, 6))ax = dta.ix[x[0]:].plot(ax=ax)predict_sunspots.plot(ax=ax)show()其实，可以通过代码来⾃动的选择p和q的值，依据BIC准则，⽬标就是bic越⼩越好代码def proper_model(timeseries, maxLag):init_bic = 100000000init_properModel = Nonefor p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q))try:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_properModel = results_ARMAinit_bic = bicreturn init_properModel遇到的问题，预测时predict函数没怎么使⽤明⽩当写于某些预测区间的时候，会报 “start”或“end”的相关错误，还有⼀个函数forcast，这个函数使⽤就是forcast(N)：预测后⾯N个值返回的是预测值（array型）标准误差（array型）置信区间（array型）还有：对于构造时间序列，时间可以是时间格式：如 “2018-01-01” 或者就是个时间戳，在⽤时间戳的时候，其实在序列⾥它会⾃动识别时间戳，并加上起始时间1970-01-01 00:00:01形式附录（代码）预测⼀序列中某⼀点的值#coding:utf-8import csvimport timeimport pandas as pdimport numpy as npfrom statsmodels.tsa.arima_model import ARMAimport argparseimport warningswarnings.filterwarnings('ignore')def timestamp_datatime(value):value = time.localtime(value)dt = time.strftime('%Y-%m-%d %H:%M',value)return dtdef time_timestamp(my_date):my_date_array = time.strptime(my_date,'%Y-%m-%d %H:%M')my_date_stamp = time.mktime(my_date_array)return my_date_stampdef read_csv_data(aim_list_1, aim_list_2, file_name):i = 0csv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[1])) #1：温度 2：湿度dt = int(data[3])aim_list_2.append(dt)returndef proper_model(timeseries, maxLag):init_bic = 100000000init_properModel = Nonefor p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q)) #bugtry:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_properModel = results_ARMAinit_bic = bicreturn init_properModeldef test_300(temp, tim, time_in):x = []y = []end_index = len(tim)for i in range(0, len(tim)):if (time_in - (tim[i]) < 300):end_index = ibreakif (end_index < 100):x = tim[0: end_index]y = temp[0: end_index]else:x = tim[end_index - 100: end_index]y = temp[end_index - 100: end_index]tidx = pd.DatetimeIndex(x, freq='infer')dta = pd.Series(y, index = tidx)print(dta)arma_mod = proper_model(dta, 9)predict_sunspots = arma_mod.forecast(1)return predict_sunspots[0]def predict_temperature(file_name, time_in):temp = []tim = []read_csv_data(temp, tim, file_name)result_temp = test_300(temp, tim, time_in)return result_tempif__name__ == '__main__':parser = argparse.ArgumentParser()parser.add_argument('-f', action='store', dest='file_name')parser.add_argument('-t', action='store', type = int, dest='time_')args = parser.parse_args()file_name = args.file_nametime_in = args.time_result_temp = predict_temperature(file_name, time_in)print ('the temperature is %f ' % result_temp)在上⾯的代码中，预测某⼀点的值我采⽤序列中此点的前100个点作为训练集如果给出待预测的多个点，由于每次都要计算模型的p和q以及拟合模型，时间会很慢，于是考虑将给定的待预测时间点序列切割成⼩段，使每⼀段中最⼤与最⼩的时间间隔在某⼀范围内在使⽤forcast(n)函数⼀次预测多点，然后在预测值中找到与待预测的时间值相近的值，速度⼤⼤提升，思路如图代码#coding:utf-8import csv#import timeimport pandas as pdimport numpy as npfrom statsmodels.tsa.arima_model import ARMAimport warningswarnings.filterwarnings('ignore')def proper_model(timeseries, maxLag):init_bic = 1000000000init_p = 1init_q = 1for p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q))try:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_p = pinit_q = qinit_bic = bicreturn init_p, init_qdef read_csv_data(file_name, clss = 1):i = 0aim_list_1 = [] #temperature(1) or humidity(2)aim_list_2 = [] #timecsv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[clss]))dt = int(data[3])aim_list_2.append(dt)tidx = pd.DatetimeIndex(aim_list_2, freq = None)dta = pd.Series(aim_list_1, index = tidx)init_p, init_q = proper_model(dta[:aim_list_2[100]], 9)return init_p, init_q, aim_list_2, dtadef for_kernel(p, q, tim, dta, tmp_time_list, result_dict):interval = 20end_index = len(tim) - 1for i in range(0, len(tim)):if (tmp_time_list[0]["time"] - tim[i] < tim[1] - tim[0]):end_index = ibreakif (end_index < 100):dta = dta.truncate(after = tim[end_index])else:dta = dta.truncate(before= tim[end_index - 101], after = tim[end_index])arma_mod = ARMA(dta, order=(p, q)).fit(disp = 0, method='css')#为未来interval天进⾏预测，返回预测结果，标准误差，和置信区间predict_sunspots = arma_mod.forecast(interval)####################################for tim_i in tmp_time_list:for tim_ in tim:if tim_i["time"] - tim_ >= 0 and tim_i["time"] - tim_ < tim[1] - tim[0]:result_dict[tim_i["time"]] = predict_sunspots[0][tim.index(tim_) - end_index] returndef kernel(p, q, tim, dta, time_in_list):interval = 20time_first = time_in_list[0]det_time = tim[1] - tim[0]result_dict = {}tmp_time_list = []for time_ in time_in_list:if time_first["time"] + det_time * interval > time_["time"]:tmp_time_list.append(time_)continuetime_first = time_for_kernel(p, q, tim, dta, tmp_time_list, result_dict)tmp_time_list = []tmp_time_list.append(time_first)for_kernel(p, q, tim, dta, tmp_time_list, result_dict)return result_dictdef predict_temperature(file_name, time_in_list, clss = 1):p, q, tim, dta = read_csv_data(file_name, clss)result_temp_dict = kernel(p, q, tim, dta, time_in_list)return result_temp_dictdef predict_humidity(file_name, time_in_list, clss = 2):p, q, tim, dta = read_csv_data(file_name, clss)result_humi_dict = kernel(p, q, tim, dta, time_in_list)return result_humi_dictif__name__ == '__main__':file_name = "testdata.csv"time_in = [{"time":1530419271,"temp":"","humi":""},{"time":1530600187,"temp":"","humi":""},{"time":1530825809,"temp":"","humi":""}] #time_in = [{"time":1530600187,"temp":"","humi":""},]result_temp = predict_temperature(file_name, time_in)print(result_temp)由于后续⼜改动了需求，需要预测温度以及湿度，完成了项⽬在github。

R 语言环境下使用ARIMA模型做时间序列预测1.序列平稳性检验通过趋势线、自相关(ACF)与偏自相关(PACF)图、假设检验和因素分解等方法确定序列平稳性，识别周期性，从而为选择适当的模型提供依据。

1.1绘制趋势线图1 序列趋势线图从图1很难判断出序列的平稳性。

1.2绘制自相关和偏自相关图图2 序列的自相关和偏自相关图从图2可以看出，ＡＣＦ拖尾，ＰＡＣＦ１步截尾（p=1），说明该现金流时间序列可能是平稳性时间序列。

1.3 ADF、PP和KPSS 检验平稳性图3 ADF、PP和KPSS检验结果通过ADF检验，说明该现金流时间序列是平稳性时间序列（p-value for ADF test <0.02，拒绝零假设）.pp test和kpss test 结果中的警告信息说明这两种检验在这里不可用。

但是这些检验没有充分考虑趋势、周期和季节性等因素。

下面对该序列进行趋势、季节性和不确定性因素分解来进一步确认序列的平稳性。

1.4 趋势、季节性和不确定性因素分解R 提供了两种方法来分解时间序列中的趋势、季节性和不确定性因素。

第一种是使用简单的对称过滤法，把相应时期内经趋势调整后的观察值进行平均，通过decompose()函数实现，如图4。

第二种方法更为精确，它通过平滑增大规模后的观察值来寻找趋势、季节和不确定因素，利用stl()函数实现。

如图5。

图4 decompose()函数分解法图5 stl()函数分解法两种方法得到的结果非常相似。

从上图可以看出，该现金流时间序列没有很明显的长期趋势。

但是有明显的季节性或周期性趋势，经分解后的不确定因素明显减少。

综上平稳性分析检验，我们选用包含季节性因素的S-ARIMA模型来预测现金流时间序列。

2．S-ARIMA模型2.1 建立SARIMA模型在R 软件包中包含auto.arima()、expand.grid() 等函数，针对p,d,q 众多的可能取值，可以通过expand.grid()建立所有的可能参数组合，用for()条件函数代入相应的arima（）模型，把结果储存在BIC当中。

时间序列分析R语言代码时间序列分解分析的R语言操作如下：选取R语言自带的数据包UKgas，即1960-1986每月英国天然气消耗的数据，并将其赋值于n：n<-UKgassummary（）函数提供了最小值、最大值、四分位数和数值型变量的均值： summary(n)画出UKgas的时序图：plot(n)时间序列分解分析方法一：基础包stats的decompose函数调用基础包stats：library("stats")利用基础包stats的decompose函数对时间序列进行分解分析，命名为fit1。

该函数基于移动平均方法，multiplicative表示使用乘法模型：fit1=decompose(n, type = c("multiplicative"))展示decompose函数的分解结果：fit1绘制方法一，即利用decompose函数分解的分解图：plot(fit1)`时间序列分解分析方法二：基础包stats的stl函数stl函数stl(x,s.window,s.degree=0,t.window = NULL, t.degree = 1, robust = FALSE,na.action = na.fail)x----待分解的变量s.window----提取季节性时的loess算法时间窗口宽度，可设为periodic，或者设为奇数并不能低于7s.degree -----提取季节性时局部拟合多项式的阶数，须为0或1 t.window----提取长期趋势性时的loess算法时间窗口宽度，缺省为NULL，或者奇数t.degree-----提取长期趋势性时的局部拟合多项式的阶数，须为0或1robust -----在loess过程中是否使用鲁棒拟合利用基础包stats的stl函数对时间序列进行分解分析，命名为fit2：fit2<-stl(n,s.window="periodic",s.degree = 0, t.window = NULL, t.degree = 1,robust= FALSE,na.action = na.fail)展示stl函数的分解结果：fit2绘制方法二的分解图： plot(fit2)。

对外汇数据进行时间序列分析时间序列存在于社会的经济、医学等很多领域，其中时间序列的趋势分析是一个具有重要现实意义的研究领域，因为人们掌握事物的发展趋势(内在规律)，就能利用这些规律制定相应的决策。

传统对时间序列的分析多从系统的角度出发，而本文对时间序列的分析是从数据挖掘的角度出发。

外汇汇率时间序列，往往含有较多的干扰因素，因此必须对原始数据进行平滑处理，尽可能的除去附加的干扰因素。

为了能够对时间序列进行数据挖掘，必须从时间序列数据中抽取决定时间序列行为发展趋势的静态属性。

数据选取首先我们从网站http://fx.sauder.ubc.ca/data.html下载CAD和USD需货币对的两年汇率，并将数据读入RDownload the exchange rate of your desired currency pairs for at least two years from the website: http://fx.sauder.ubc.ca/data.html, and read the data into R. （5 points）浏览数据dataJul.Day YYYY.MM.DD Wdy D1 2457025 2015/01/02 Fri 0.651012 2457028 2015/01/05 Mon 0.656443 2457029 2015/01/06 Tue 0.658964 2457030 2015/01/07 Wed 0.663445 2457031 2015/01/08 Thu 0.66151...576 2457864 2017/04/20 Thu 0.77942577 2457865 2017/04/21 Fri 0.78233578 2457868 2017/04/24 Mon 0.78227579 2457869 2017/04/25 Tue 0.77907580 2457870 2017/04/26 Wed 0.77896581 2457871 2017/04/27 Thu 0.77587582 2457872 2017/04/28 Fri 0.77299583 2457875 2017/05/01 Mon 0.77420584 2457876 2017/05/02 Tue 0.77392585 2457877 2017/05/03 Wed 0.77476586 2457878 2017/05/04 Thu 0.77456587 2457879 2017/05/05 Fri 0.77177588 2457882 2017/05/08 Mon 0.77263589 2457883 2017/05/09 Tue 0.77337590 2457884 2017/05/10 Wed 0.77278591 2457885 2017/05/11 Thu 0.77656592 2457886 2017/05/12 Fri 0.77651593 2457889 2017/05/15 Mon 0.77479594 2457890 2017/05/16 Tue 0.77466595 2457891 2017/05/17 Wed 0.77186596 2457892 2017/05/18 Thu 0.76994597 2457893 2017/05/19 Fri 0.76776598 2457897 2017/05/23 Tue 0.77037599 2457898 2017/05/24 Wed 0.77232600 2457899 2017/05/25 Thu 0.77218601 2457900 2017/05/26 Fri 0.78092绘制时间序列图收集历史资料，加以整理，编成时间序列，并根据时间序列绘成统计图。

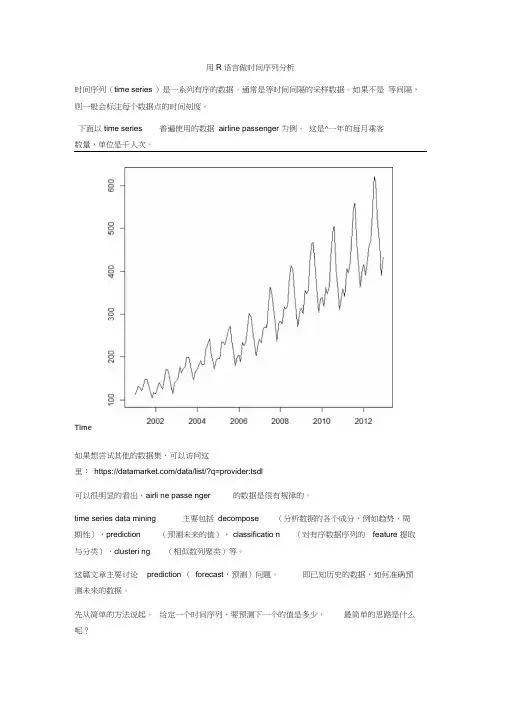
用R语言做时间序列分析时间序列（time series ）是一系列有序的数据。

通常是等时间间隔的采样数据。

如果不是等间隔，则一般会标注每个数据点的时间刻度。

下面以time series 普遍使用的数据airline passenger 为例。

这是^一年的每月乘客数量，单位是千人次。

Time如果想尝试其他的数据集，可以访问这里：https:///data/list/?q=provider:tsdl可以很明显的看出，airli ne passe nger 的数据是很有规律的。

time series data mining 主要包括decompose （分析数据的各个成分，例如趋势，周期性），prediction （预测未来的值），classificatio n （对有序数据序列的feature 提取与分类），clusteri ng （相似数列聚类）等。

这篇文章主要讨论prediction （forecast，预测）问题。

即已知历史的数据，如何准确预测未来的数据。

先从简单的方法说起。

给定一个时间序列，要预测下一个的值是多少，最简单的思路是什么呢？（1）m ean （平均值）：未来值是历史值的平均。

（2）exponential smoothing （指数衰减）：当去平均值得时候，每个历史点的权值可以不一样。

最自然的就是越近的点赋予越大的权重。

= aX± + ct^X2 + a3X3+ …或者，更方便的写法，用变量头上加个尖角表示估计值X t+1 = aX t+ （1 - a）X t（3） sn aive :假设已知数据的周期，那么就用前一个周期对应的时刻作为下一个周期对应时刻的预测值（4）d rift :飘移，即用最后一个点的值加上数据的平均趋势tX t+h|t =禺+占2心-斗-丄= x t +占（罠-如Tt = •介绍完最简单的算法，下面开始介绍两个time series 里面最火的两个强大的算法：Holt-Winters 和ARIMA 。

奶牛月产奶量的时间序列分析本文应用R软件对奶牛月产奶量建立时间序列模型并进行预测。

文章主要从以下几个方面进行：1.描述性统计2.模型识别3.参数估计4.模型诊断5.预测6.其他建模方法及效果对比7.结论最终通过多方面对比，我们选择了ARIMA(0,1,1)×(0,1,1)12模型用于以后数据的预测。

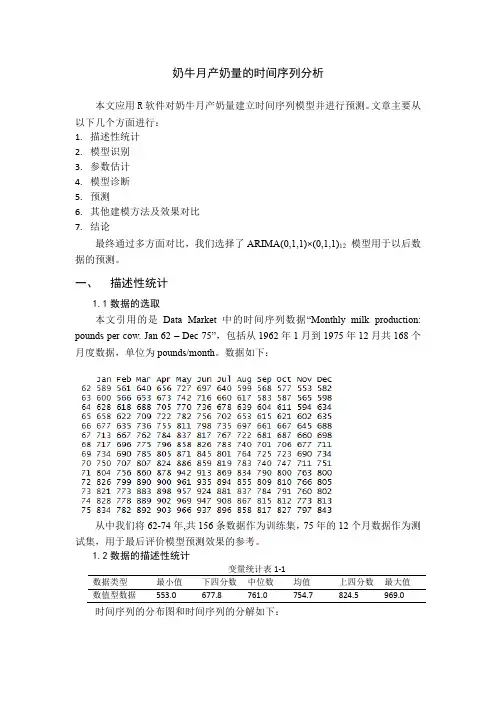
一、描述性统计1.1数据的选取本文引用的是Data Market中的时间序列数据“Monthly milk production: pounds per cow. Jan 62 –Dec 75”，包括从1962年1月到1975年12月共168个月度数据，单位为pounds/month。

数据如下：从中我们将62-74年,共156条数据作为训练集，75年的12个月数据作为测试集，用于最后评价模型预测效果的参考。

1.2数据的描述性统计变量统计表1-1数据类型最小值下四分数中位数均值上四分数最大值数值型数据553.0 677.8 761.0 754.7 824.5 969.0时间序列的分布图和时间序列的分解如下：时间序列分解图1-1由图可以看出，时间序列含有明显的季节性和上升趋势，且没有波动集群现象，可以考虑季节模型，最常用的是ARIMA模型。

1.3乘法季节模型乘法季节模型是随机季节模型与 ARIMA 模型的结合。

统计学上纯 RIMA （p，d， q ）模型记作：ΦΘ。

其中 t 代表时间，Xt 表示响应序列，B是后移算子， R=1-B，p、 d、 q 分别表示自回归阶数、差分阶数和移动平均阶数；Φ(B)表示自回归算子；Θ(B)表示滑动平均算子。

一个阶数为（P，d， q ）×（P， D， Q ） s 的乘积季节模型可表为：ΦΘ代表独立干扰项或随机误差项， s 的值是一个季节循环中观测的个数，atΦ表示同一周期内不同周期点的相关关系，则描述了不同周期中对应时点上的相关关系，二者结合起来便同时刻画了 2 个因数的作用。

第三次试验报告一、实验目的：根据AR模型、MA模型所学知识,利用R语言对数据进行AR、MA模型分析，得出实验结果并对数据进行一些判断，选择最优模型。

二、实验要求：三、实验步骤及结果：⑴建立新的文件夹以及R-project，将所需数据移入该文件夹中。

⑵根据要求编写代码，如下所示：为例）代码及说明：（以r t2⑶实验结果及相关说明：时间序列1；1.确定模型①时序图（TS图）：由图可知：该时间序列可能具有平稳性，均值在0附近。

②自相关函数图（ACF图）：由图可知：很快减小为0（q=0）2.定阶③偏相关函数（PACF图）由图可知，PACF图0步结尾。

3.参数估计：4. 模型诊断：（法一）利用tsdiag(fit1) 函数进行整体检验：对模型诊断得出下面一组图，每组包含三个小图：i第一个小图为标准化残差图，是ât/σ所得。

模型图看不出明显规律。

ii第二个小图为残差ât的自相关函数图，是单个ρk是否等于0的假设检验。

（蓝线置信区间内都可认为是0）可知：模型中单个ρk都等于0假设成立。

iii第三个小图为前m个ρk同时为0的L-B假设检验。

则由模型图知：在95%置信区间下认为ât为白噪声，模型充分性得到验证。

（法二）利用Box-Ljung test 进行检验：5. 拟合优度检验：①调整后R2：Adj-R2=1 - σ̂a2/σ̂r2②信噪比: SNR=σ̂r2/σ̂a2=[1/(1- Adj-R2)]-1由结果可知：Adj-R2= 0.001428571;信噪比SNR= 0.001430615;即由Adj-R2=14.28571% 较低，说明说明信号占整体数据信息比例较小，模型拟合效果不够好。

由SNR可知，噪音约为信号700倍，模型效果非常不好。

6. 预测：时间序列2：1.确定模型①时序图（TS图）：由图可知：该时间序列具有平稳性。

②自相关函数图（ACF图）：由图可知：很快减小为0，并呈周期性、指数衰减,并且3步结尾。

J I A N G S U U N I V E R S I T Y江苏省餐饮业零售总额分析预测学校：江苏大学学院：财经学院班级：统计1201组员：韩亚琼3120812015马海燕3120812022顾君颖3120812020王培培3120812009陆金龙3120812029白卓3120812028完成时间：2014年12月13日星期六一、摘要二、引言三、数据分析原始数据的获取：本文所有的样本数据均来自《江苏统计年鉴——2014》（/2014nj/nj14.htm）得到的样本数据参见表1：表1 按行业分社会消费品零售总额这里我们仅用到第三列数据，为了方便分析，我们将餐饮业零售总额序列命名为caterts。

第一步序列的平稳性检验为判断一个序列是否平稳，我们主要通过时序图以及自相关图进行检验。

对caterts做时序图，有图形发现有明显的指数趋势，序列非平稳，也可以初步发现江苏省的餐饮业零售总额逐年递增，尤其是在新世纪以后，人们的生活水平逐年提高，对餐饮业的贡献也增大：图1 caterts序列时序图因为原序列有明显的指数趋势，故先对数列进行对数变换得到新的数列logcatets，序列图如下，具有明显的非线性增长趋势：图2 对数化后的时序图对具有明显线性趋势的数列常用的平稳化措施是差分，我们对logcaterts序列进行一阶差分得到新的数列difflogcaterts，时序图如下：图3 对数化和一阶差分后的时序图通过对时序图分析发现数列具有平稳性，为了方便分析，我们对difflogcaterts 序列进行中心化处理，得到新的数列x。

对x进行ADF检验（单位根检验）。

R语言中有专门的fUnitRoots包，里面有urdftest功能，是专门进行序列的ADF单位根检验，通过R软件得到如下结果：Title:Augmented Dickey-Fuller Unit Root TestTest Results:Test regression noneCall:lm(formula = z.diff ~ g.1 - 1 + g)Residuals:Min 1Q Median 3Q Max-0.224894 -0.051073 0.006261 0.043257 0.242110Coefficients:Estimate Std. Error t value Pr(>|t|)g.1 -0.59259 0.19455 -3.046 0.0047 **g 0.02909 0.18067 0.161 0.8731---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 0.08821 on 31 degrees of freedomMultiple R-squared: 0.2853, Adjusted R-squared: 0.2392F-statistic: 6.188 on 2 and 31 DF, p-value: 0.005481Value of test-statistic is: -3.046Critical values for test statistics:1pct 5pct 10pcttau1 -2.62 -1.95 -1.61从结果可以看出ADF统计量为-3.046，在1%，5%，10%的置信水平下均拒绝原假设，认为序列x平稳。

时间序列分析R语言程序时间序列分析是一种研究数据随时间变化的趋势、周期性和不规则性的方法。

它在许多领域中都有广泛的应用，包括经济学、金融学、气象学和工程学等。

R语言是一种非常适合进行时间序列分析的编程语言，它提供了丰富的工具包和函数来进行数据处理、模型建立和预测。

为了进行时间序列分析，首先需要加载相关的R包，例如“ts”和“forecast”。

然后，可以使用“read.csv”函数将时间序列数据导入R 中。

以下是一个示例代码：```R#加载相关包library(ts)library(forecast)#导入时间序列数据data <- read.csv("data.csv")#将数据转换为时间序列对象ts_data <- ts(data$Value, start = c(year(data$Date)[1], month(data$Date)[1]), frequency = 12)#绘制时间序列图plot(ts_data, main = "Time Series Plot", xlab = "Date", ylab = "Value")#拟合时间序列模型model <- auto.arima(ts_data)#显示模型的摘要信息summary(model)#进行未来预测forecast <- forecast(model, h = 12)print(forecast)```上述代码中，首先加载了“ts”和“forecast”两个R包，然后使用“read.csv”函数导入了名为“data.csv”的时间序列数据文件。

数据文件中应包含“Date”和“Value”两列，分别表示时间和对应的数值。

接着，使用“ts”函数将导入的数据转换为时间序列对象。

在这个例子中，假设数据按月份记录，函数中的“start”参数指定了时间序列的起始年份和月份，而“frequency”参数表示每年包含的时间周期数。

R语言季节性arima模型案例代码数据文件sales.csv提供公司季度销售数据。

为这些数据构建时间序列图。

描述数据。

data=read.csv("sales.csv")head(data)## sales## 1 105715## 2 120136## 3 181669## 4 239813## 5 159980## 6 164760plot(as.numeric(data[,1]),type="l")# 分解为趋势和季节成分# 从数据来看，有明显得波动趋势，因此可能存在季节性趋势，需要进行季节性差分。

# 计算趋势（使用适当的移动平均线）和季节性成分。

将时间趋势，季节性因素和剩余序列与时间对应，并对您的地块进行评论。

kingstimeseries <-ts(as.numeric(data[,1]),frequency =12)kingstimeseries## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec## 1 3 8 19 25 14 15 24 29 21 23 28 33## 2 26 27 31 37 30 32 36 41 34 35 39 44## 3 38 40 47 50 42 43 51 55 45 46 54 4## 4 48 49 56 9 52 53 7 13 5 6 12 16## 5 10 11 18 22 17 20 2 1kingstimeseriescomponents <-decompose(kingstimeseries)kingstimeseriescomponents$seasonal # get the estimated values of the s easonal component## Jan Feb Mar Apr May Jun ## 1 -1.1649306 0.6059028 7.7934028 -4.4149306 5.3767361 7.1684028 ## 2 -1.1649306 0.6059028 7.7934028 -4.4149306 5.3767361 7.1684028 ## 3 -1.1649306 0.6059028 7.7934028 -4.4149306 5.3767361 7.1684028 ## 4 -1.1649306 0.6059028 7.7934028 -4.4149306 5.3767361 7.1684028 ## 5 -1.1649306 0.6059028 7.7934028 -4.4149306 5.3767361 7.1684028 ## Jul Aug Sep Oct Nov Dec ## 1 -2.1753472 2.7204861 -5.5503472 -4.2586806 1.4913194 -7.5920139 ## 2 -2.1753472 2.7204861 -5.5503472 -4.2586806 1.4913194 -7.5920139 ## 3 -2.1753472 2.7204861 -5.5503472 -4.2586806 1.4913194 -7.5920139 ## 4 -2.1753472 2.7204861 -5.5503472 -4.2586806 1.4913194 -7.5920139 ## 5 -2.1753472 2.7204861plot(kingstimeseriescomponents)# 从差分图来看，数据有明显得季节趋势，需要进行季节性差分。

【原创】R语言股票回归、时间序列分析报告论文附代码数据论文题目：股票价格回归分析报告摘要：主要思路为了准确的估计股票价格,了解股票的一般规律,更好的为资本市场提供参考意见和帮助股民进行投资股票作出正确的决策,本文从股票价格指数与整个经济环境角度出发,采用多元回归分析方法,应用月度时间序列数据,通过选取综合反映股票市场上所有公司股票价格整体水平的指标建立了线性回归模型,得出了股票价格趋势变动的影响因素.关键词：回归模型；指数模型；股票价格；预测一、引言主要思路为了准确的估计股票价格，本文从股票价格指数与整个经济环境角度出发,采用多元回归分析方法,应用月度时间序列数据建立了线性回归模型,具体分析步骤：1.关系分析基于以上原理,为大致了解股票价格与诸因素之间的关系,先分别绘制股票价格与各个因素之间的散点图,并分析它们之间的关系.股价用上证A股指数来表示,这样可以减少人为因素对股票价格的影响,尽量将注意力集中在我们假设选用的自变量上.我们采用的数据是2012年和2015年上半年的月度数据,分析影响我国股市趋势的因素。

之所以选取2012年和2015年7月的统计资料是基于以下两点考虑：中国股市发展时间较短,采用年度数据会因为样本量太小而使得回归分析失去意义;数据取得的存在较大难度,因季度数据不全而只能选取月度数据.因此选取2012年和2015年7月份月度数据作为样本.2.指数光滑时间序列展望模子3.挑选多项式回来模子3.1变量选取通过向前向后逐步迭代回归模型筛选出显著性较强的变量进行回归建模。

3.2明显性检修根据F值和p值统计量来判别模子是不是具有明显的统计意义。

3.3拟合预测使用得到的模型对实际数据进行拟合和预测。

4.分析得出结论得出各个自变量之间的关系，和它们对因变量的影响极端经济意义。

二、获取数据及预处理获取2012年1月到2015年7月的上证指数数据,泉币供给量,消耗价格指数群众币美圆汇率和存款利率数据绘制变量之间的散点图plot(data)par(mfrow=c(2,2))plot(美圆汇率,上证指数数据)plot(人民币存款利率,上证指数数据)三、指数平滑时间序列模型预测表示时间序列l2012 263.670 19.925 240.655 131.620 245.665 368. -51.615 -156.545 69.235 -46.705 -329.040 -181.635 -2. -65.535 87.565 79.200 37.740 -157.900 -118.655 59. -50.230 142.300 -11.580 -25.710 47.830 -92.995 -115.865Aug Sep Oct Nov Dec2012 -130.350 -216.610 125.145 163.415 44.4802013 145.310 5.895 236.405 97.135 -142.5552014 -176.755 -108.775 -71.055 32.655 -149.3202015Jan Feb Mar Apr May Jun Ju利用HoltWinters函数展望：p.hw<-XXX,h=24)h=24透露表现展望24个值四、进行多元回归模型并进行分析summary(lmmod)显示回来成效Call:lm(formula = y ~ x1 + x2 + x3 + x4, data = data)Residuals:Min 1Q Median 3Q Max-543.94 -90.09 1.69 113.01 500.68Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) -3.457e+04 9.319e+03 -3.710 0. ***x1 3.325e-03 1.369e-03 2.430 0. *x2 1.341e+01 2.663e+01 0.503 0.x3 4.787e+01 1.400e+01 3.420 0. **x4 7.870e+02 3.380e+02 2.328 0. *---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 246.5 on 38 degrees of freedomMultiple R-squared: 0.4804, Adjusted R-squared: 0.4257F-statistic: 8.783 on 4 and 38 DF, p-value: 4.012e-05回来成效分析从输出成效能够看出，回来方程为，变量和的统计量的估量值分别为-3.457e+04， 3.325e-03， 1.341e+01，4.787e+01和7.870e+02，除x2以外由对应的值都比显著性水平0.05小，可得两个偏回归系p数在显著性水平0.05下均显著不为零。

时间序列分析之ARIMA模型预测__R篇相关⽂章：时间序列分析之ARIMA模型预测__SAS篇之前⼀直⽤SAS做ARIMA模型预测，今天尝试⽤了⼀下R，发现灵活度更⾼，结果输出也更直观。

现在记录⼀下如何⽤R分析ARIMA模型。

1. 处理数据1.1. 导⼊forecast包forecast包是⼀个封装的ARIMA统计软件包，在默认情况下，R没有预装forecast包，因此需要先安装该包> install.packages("forecast')导⼊依赖包zoo，再导⼊forecast包> library("zoo")> library("forecast")1.2. 导⼊数据博主使⽤的数据是⼀组航空公司的销售数据，可在此下载数据：，共有132条数据，是以⽉为单位的销售数据。

> airline <- read.table("airline.txt")> airline V1 V2 1 1 112 2 2 118 3 3 132 4 4 129 5 5 121 6 6 135 7 7 148 8 8 148 9 9 136 10 10 119(........)1.3. 将数据转化为时间序列格式(ts)由于将数据转化为时间序列格式，我们并不需要时间字段，因此只取airline数据的第⼆列，即销售数据，⼜因为该数据是以⽉为单位的，因此Period是12。

> airline2 <- ariline[2]> airts <- ts(airline2,start=1,frequency=12)2. 识别模型2.1. 查看趋势图> plot.ts(airts)由图可见，该序列还不平稳，先做⼀次Log平滑，再做⼀次差分:> airlog <- log(airts)> airdiff <- diff(airlog, differences=1)> plot.ts(airdiff)这次看上去就⽐较平稳了，现在看看ACF和PACF的结果2.2. 查看ACF和PACF> acf(airdff, lag.max=30)> acf(airdff, lag.max=30,plot=FALSE)Autocorrelations of series ‘airdiff’, by lag0.00000.08330.16670.25000.33330.41670.50000.58330.66670.75000.83331.0000.188 -0.127 -0.154 -0.326 -0.0660.041 -0.098 -0.343 -0.109 -0.1200.91671.00001.08331.16671.25001.33331.41671.50001.58331.66671.75000.1990.8330.198 -0.143 -0.110 -0.288 -0.0460.036 -0.104 -0.313 -0.1061.83331.91672.00002.08332.16672.25002.33332.41672.5000-0.0850.1850.7140.175 -0.126 -0.077 -0.214 -0.0460.029> pacf(airdff, lag.max=30)> pacf(airdff, lag.max=30,plot=FALSE)Partial autocorrelations of series ‘airdiff’, by lag0.08330.16670.25000.33330.41670.50000.58330.66670.75000.83330.91670.188 -0.169 -0.101 -0.3170.018 -0.072 -0.199 -0.509 -0.171 -0.553 -0.3001.00001.08331.16671.25001.33331.41671.50001.58331.66671.75001.83330.5510.010 -0.2000.164 -0.052 -0.037 -0.1080.0940.005 -0.095 -0.0011.91672.00002.08332.16672.25002.33332.41672.50000.057 -0.074 -0.0480.0240.0730.0470.0100.033从ACF和PACF可以看出来，该序列在lag=12和lag=24处有明显的spike，说明该序列需要再做⼀次diff=12的差分。

R语言-时间序列时间序列:可以用来预测未来的参数,1.生成时间序列对象1 sales <- c(18, 33, 41, 7, 34, 35, 24, 25, 24, 21, 25, 20,2 22, 31, 40, 29, 25, 21, 22, 54, 31, 25, 26, 35)3# 1.生成时序对象4 tsales <- ts(sales,start = c(2003,1),frequency = 12)5 plot(tsales)6# 2.获得对象信息7 start(tsales)8 end(tsales)9 frequency(tsales)10# 3.对相同取子集11 tsales.subset <- window(tsales,start=c(2003,5),end=c(2004,6))12 tsales.subset 结论:手动生成的时序图2.简单移动平均案例:尼罗河流量和年份的关系1 library(forecast)2 opar <- par(no.readonly = T)3 par(mfrow=c(2,2))4 ylim <- c(min(Nile),max(Nile))5 plot(Nile,main='Raw time series')6 plot(ma(Nile,3),main = 'Simple Moving Averages (k=3)',ylim = ylim)7 plot(ma(Nile,7),main = 'Simple Moving Averages (k=3)',ylim = ylim)8 plot(ma(Nile,15),main = 'Simple Moving Averages (k=3)',ylim = ylim)9 par(opar) 结论:随着K值的增大,图像越来越平滑我们需要找到最能反映规律的K值3.使用stl做季节性分解案例:Arirpassengers年份和乘客的关系1# 1.画出时间序列2 plot(AirPassengers)3 lAirpassengers <- log(AirPassengers)4 plot(lAirpassengers,ylab = 'log(Airpassengers)')5# 2.分解时间序列6 fit <- stl(lAirpassengers,s.window = 'period')7 plot(fit)8 fit$time.series9 par(mfrow=c(2,1))10# 3.月度图可视化11 monthplot(AirPassengers,xlab='',ylab='')12# 4.季度图可视化13 seasonplot(AirPassengers,bels = T,main = '') 原始图 对数变换 总体趋势图 月度季度图4.指数预测模型 4.1单指数平滑 案例:预测康涅狄格州的气温变化# 1.拟合模型fit2 <- ets(nhtemp,model = 'ANN')fit2# 2.向前预测forecast(fit2,1)plot(forecast(fit2,1),xlab = 'Year',ylab = expression(paste("Temperature (",degree*F,")",)),main="New Haven Annual Mean Temperature")# 3.得到准确的度量accuracy(fit2) 结论:浅灰色是80%的置信区间,深灰色是95%的置信区间 4.2有水平项,斜率和季节项的指数模型 案例:预测5个月的乘客流量1# 1.光滑参数2 fit3 <- ets(log(AirPassengers),model = 'AAA')3 accuracy(fit3)4# 2.未来值预测5 pred <- forecast(fit3,5)6 pred7 plot(pred,main='Forecast for air Travel',ylab = 'Log(Airpassengers)',xlab = 'Time') 8# 3.使用原始尺度预测9 pred$mean <- exp(pred$mean)10 pred$lower <- exp(pred$lower)11 pred$upper <- exp(pred$upper)12 p <- cbind(pred$mean,pred$lower,pred$upper)13 dimnames(p)[[2]] <- c('mean','Lo 80','Lo 95','Hi 80','Hi 95')14 p 结论:从表格中可知3月份的将会有509200乘客,95%的置信区间是[454900,570000] 4.3ets自动预测 案例:自动预测JohnsonJohnson股票的趋势1 fit4 <- ets(JohnsonJohnson)2 fit43 plot(forecast(fit4),main='Johnson and Johnson Forecasts',4 ylab="Quarterly Earnings (Dollars)", xlab="Time") 结论:预测值使用蓝色线表示,浅灰色表示80%置信空间,深灰色表示95%置信空间5.ARIMA预测步骤: 1.确保时序是平稳的 2.找出合理的模型(选定可能的p值或者q值) 3.拟合模型 4.从统计假设和预测准确性等角度评估模型 5.预测library(tseries)plot(Nile)# 1.原始序列差分一次ndiffs(Nile)dNile <- diff(Nile)# 2.差分后的图形plot(dNile)adf.test(dNile)Acf(dNile)Pacf(dNile)# 3.拟合模型fit5 <- arima(Nile,order = c(0,1,1))fit5accuracy(fit5)# 4.评价模型qqnorm(fit5$residuals)qqline(fit5$residuals)Box.test(fit5$residuals,type = 'Ljung-Box')# 5.预测模型forecast(fit5,3)plot(forecast(fit5,3),xlab = 'Year',ylab = 'Annual Flow') 原始图 一次差分图形1 fit6 <- auto.arima(sunspots)2 fit63 forecast(fit6,3)4 accuracy(fit6)5 plot(forecast(fit6,3), xlab = "Year",6 ylab = "Monthly sunspot numbers")。

使用R语言进行时间序列（arima，指数平滑）分析读时间序列数据您要分析时间序列数据的第一件事就是将其读入R，并绘制时间序列。

您可以使用scan（）函数将数据读入R，该函数假定连续时间点的数据位于包含一列的简单文本文件中。

数据集如下所示：Age of Death of Successive Kings of England#starting with William the Conqueror#Source: McNeill, "Interactive Data Analysis"604367505642506568436534...仅显示了文件的前几行。

前三行包含对数据的一些注释，当我们将数据读入R时我们想要忽略它。

我们可以通过使用scan（）函数的“skip”参数来使用它，它指定了多少行。

要忽略的文件顶部。

要将文件读入R，忽略前三行，我们键入：> kings[1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48[26] 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56在这种情况下，英国42位连续国王的死亡年龄已被读入变量“国王”。

一旦将时间序列数据读入R，下一步就是将数据存储在R中的时间序列对象中，这样就可以使用R的许多函数来分析时间序列数据。

要将数据存储在时间序列对象中，我们使用R中的ts（）函数。

例如，要将数据存储在变量'kings'中作为R中的时间序列对象，我们键入：Time Series:Start = 1End = 42Frequency = 1[1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48[26] 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56有时，您所拥有的时间序列数据集可能是以不到一年的固定间隔收集的，例如，每月或每季度。