当前位置：文档之家 › 磁场中的磁介质

磁场中的磁介质

  • 格式：docx
  • 大小：204.29 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

磁场中的磁介质

磁场中的磁介质
矩
e ev 电子电流 I 2r / v 2r ev evr 2 m IS r 2r 2
m en
I S
e L 2m e
角动量 L me vr
二、原子的磁矩
2.电子的量子轨道磁矩
h L m, m 0,1,2, 1.05 10 34 J S 2 e 24 一个可能的值 m 9.27 10 J / T 2m e
分子电流为
dI n a 2 dr cos i
n m dr cos
M dr cos M dr


dI M dr
三、磁介质的磁化
若 dr 选在磁介质表面，则 d I 为面束缚电流。
面束缚电流密度
dI M cos M r j dr
电流为i，半径为 a，分子磁 矩为 m ,任取一微小矢量 dr 2 a 元 dr ，它与外磁场 B 的夹角 m i 为，则与 dr 套住的分子电 流的中心都是位于以为 dr 轴、 以 a2 为底面积的斜柱体内。 i
m
B
三、磁介质的磁化
若单位体积内的分子数为n ，则与 dr 套连的总
2.磁化强度
单位体积内分子磁矩的矢量和称作磁介质的 磁化强度。 mi M V
单位 安每米（A/m）
3.实验规律
实验发现，在外磁场不是很强时，对所有磁 介质
r 1 M BB
0 r
三、磁介质的磁化
3.束缚电流与磁化强度之间的关系
以顺磁质为例 , 等效分子
电子的自旋磁矩（内禀磁矩） 电子自旋角动量 内禀磁矩
s 2
玻尔磁子
e e mB s 9.27 10 24 J / T me 2me

第7章磁场中的磁介质.ppt

第7章磁场中的磁介质.ppt
第7章 磁介质
§7.1 磁介质对磁场的影响
§7.2 原子的磁矩
§7.3 磁介质的磁化
§7.4 H的环路定理
§7.5 铁磁质 §7.6 简单的磁路
1
一、磁介质 二、 磁介质磁化的微观机理
三、磁化电流与磁化强度
四、H的环路定理 五、铁磁质 六、简单的磁路
2
一、磁介质
1.磁介质的定义 在磁场中会受磁场影响而发生 变化,反过来又对磁场产生影响 的物质就叫磁介质. 2.磁介质对磁场的影响 均匀介质充满磁 场的情况下
得：
H dr I 0内
L
•H 的单位： A/m （ SI ）；
•真空： M 0 ，H B
0
18
2. B, M , H 的关系
各向同性磁介质 r 1 将 M B 代入 0 r 各向同性电介质 P 0 r 1E D 0E P
3. 磁化规律
各向同性磁介质 (顺磁质或抗磁质)
各向同性电介质
r 1 1 1 M B (1 ) B 0 r 0 r
P 0 r 1E
0 r
介质的 磁导率
0 r
介质的介 电常数
15
四、H的环路定理 1. H的环路定理
L
NI H nI 2πr 细螺绕环
R1 R2 r
O R1 r R2
22
NI H nI 2πr
B H nI
M ( r 1) H ( r 1)nI
j M 表
代入数据
M 7.94 10 A/m
5
7.94 10 5 A/m j
23
j 7.94 10 A/m

第11章磁场中的磁介质

第11章磁场中的磁介质

Bo
向，介质内部的磁场迅
速增加，在铁磁质充磁
过程中伴随着发声、发
热。
2.磁畴的形成
按照量子理论, 铁磁质内电子间存在着很强的由电子自旋引起的相互 作用——电子交换作用, 使各电子的自旋磁矩排列整齐，从而形成磁畴。 每个磁畴内的电子自旋磁矩整齐排列，磁性很强——自发磁化。
3.磁畴与外磁场的关系
无外磁场时, 各个磁畴由于热运动其方向排列无序, 因而整体对外 不显磁性。
顺磁质和抗磁质的磁性很弱，统称弱磁质；铁磁质的磁性很强，且具有非 线性和磁滞特性。
二、 介质的磁化
任何物质皆由原子或分子构成。 原子（分子）中的电子同时参与两种运 动：自旋及绕核的轨道运动，对应有轨 道磁矩和自旋磁矩。
分子电流——分子中所有电子对外产生 的磁效应的总和可用一用等效的分子电 流的磁效应来表示
磁场强度的单位：安培/米(A/m)
§ 11.2 铁磁质
在工程技术上常用的磁介质是铁磁质，如电机、变压器和电表等。铁 磁质比顺磁质和抗磁质的磁性均要复杂。
磁化曲线——磁介质内磁感 应强度B随磁场强度H的变化 关系曲线（B~H曲线）。
顺磁质和抗磁质的磁化曲 线为直线，即B与H成线性 关系；而铁磁质则不同， 具有非线性和磁滞性。
1.超导体的基本性质
零电阻率
超导体在临界温度以下时，电阻为零，所以它可以通过很大的电流， 而几乎无热损耗。
有人曾用超导体做成一个圆环，当把它冷却到临界温度以下后，突然 去掉磁场，由于电磁感应，在超导体环内产生一个相当强的电流，这 个电流在持续两年半的时间内仍没发现可观的变化。
2. 迈斯纳效应— 完全抗磁性
利用这种现象可制成超导 重力仪，用来预测地震， 当地震发生之前，地表面 的重力场会发生变化，超 导球的位置也会发生变化， 由此来预测地震。

大物电磁学磁场中的磁介质

大物电磁学磁场中的磁介质
分界面半径 R。再求此载流系统的磁感应 强度分布。（第一层介质的相对磁导率为r1 第二层介质的磁导率为2 ）
安培环路形状：以载流体的轴线为圆心、半
径 r、且所围平面垂直轴
的圆周。
安培环路定理左边 HdlH2r
圆柱内 r R1
L
Iint
I1
R12
r2
I1 R 12
r
2
根据 H
的安培环路定理
Hdl L
Hdl
L
I0int
②物理意义
沿任一闭合路径磁场强度的环流等于该 闭合路径所包围的自由电流的代数和。
③ 理解和应用 路内总自由电流，路上总磁场强度
用 H 的环路定理求 H 与前面所学的用 B 的环路定理求 B 的方法完全相同。
（同样的应用条件；在相同载流体的情况下 ，取同样的安培环路）
三、H 和 B 的相互关系
4. 磁化强度矢量 M 与磁化面电流密度 j′的关系
介质的体积为：V lS
I′
M
MmjlSj
l
V Sl
更一般的证明为： jM en
即磁化电流密度等于磁化强度沿该表 面处的分量。
M
B
5. 磁化强度M与束缚电流 I ′的关系
LM dlM l
j l
I
磁化强度M沿闭合回路的线积分等于 该回路包围的磁化电流代数和。
B r0 H H （点点对应关系）
相对磁导率 绝对磁导率
磁介质的磁化规律可与电介质的极化规律对比：
电极化现象原 因PP 与E的关 D系 SD .dS q0
(peql) P0(r1)E D0EP,
磁化现象(原pm因iSM ) M M与 B 的 r0r1B关 H H(D系 SH .Bd 0El) M,I0

磁场中的磁介质ppt

磁场中的磁介质ppt

第五版
一、 H矢量的安培环路定理
几点说明
15
磁场中的介质

H dl I0
L
（1）只与传导电流有关，与束缚电流无关
（2） H 与 D 一样是辅助量，描述电磁场
ED

B H
B 0 H
9
（3）在真空中： M 0 r 1
第五版
15
磁场中的介质
当外磁场由 H m 逐渐减小时，这种 B 的变化落后于H的变 化的现象，叫做磁滞 现象 ，简称磁滞. 由于磁滞， H 0 时，磁感强度 B 0 Br 叫做剩余磁感强 ， 度(剩磁).
Bm
H m Br
B
Q
P
Hm
H
O
P
'
Hc
Bm
磁滞回线 矫顽力
Hc
17
第七章 恒定磁场
r
第七章 恒定磁场
13
物理学
第五版
15
磁场中的介质
解 rd R
B H
dR
0 r I
H dl I
l
2π dH I
2π d H dl I I 0
l
r
I
2π dH 0 , H 0
d
I
B H 0
同理可求 d r , B 0
物理学
第五版
15
磁场中的介质
3 铁磁性材料 不同铁磁性物质的磁滞回线形状相差很大.
B B B
O
H
O
H
O
H
软磁材料
硬磁材料
第七章 恒定磁场
矩磁铁氧体材料

9-磁介质 大学物理

9-磁介质 大学物理

当线圈中通入电流后，在磁化场的力矩作用下， 当线圈中通入电流后，在磁化场的力矩作用下，各分子环 流的磁矩在一定程度上沿着场的方向排列起来，此时， 流的磁矩在一定程度上沿着场的方向排列起来，此时，软 铁棒被磁化了。 铁棒被磁化了。
对于各向同性的均匀介质，介质内部各分子电流相互抵消， 对于各向同性的均匀介质，介质内部各分子电流相互抵消， 而在介质表面，各分子电流相互叠加， 而在介质表面，各分子电流相互叠加，在磁化圆柱的表面出 磁化面电流（ 现一层电流，好象一个载流螺线管，称为磁化面电流 现一层电流，好象一个载流螺线管，称为磁化面电流（或安 培表面电流） 培表面电流）。
(2)电子自旋磁矩 (2)电子自旋磁矩 实验证明： 实验证明：电子有自旋磁矩
ps = 0.927×10-23 A⋅m2 0.927×
(3)分子磁矩 (3)分子磁矩 分子磁矩是分子中所有电子的轨道磁矩和自旋磁矩 与所有核磁矩的矢量和。 与所有核磁矩的矢量和。 三.顺磁质与抗磁质的磁化 顺磁质与抗磁质的磁化 1、顺磁质及其磁化（如铝、 1、顺磁质及其磁化（如铝、铂、氧) 分 子 磁 矩 分子的固有磁矩不为零 pm ≠ 0 无外磁场作用时， 无外磁场作用时，由 于分子的热运动， 于分子的热运动，分 子磁矩取向各不相同, 子磁矩取向各不相同 整个介质不显磁性。 整个介质不显磁性。
B0
I0 Is
Is——磁化电流 磁化电流 js——沿轴线单位长度上的磁 沿轴线单位长度上的磁 化电流（磁化面电流密度） 化电流（磁化面电流密度）
3、磁化强度和磁化电流密度之间的关系： 磁化强度和磁化电流密度之间的关系：
以长直螺线管中的圆柱形磁介质来说明它们的关系。 以长直螺线管中的圆柱形磁介质来说明它们的关系。
磁场中的磁介质

磁场中磁介质

磁场中磁介质

磁介质的分类
顺磁性介质
抗磁性介质
铁磁性介质
反铁磁性介质
在磁场中容易被磁化的 物质，如铝、铂等。
在磁场中不容易被磁化 的物质，如铜、金等。
在磁场中极易被磁化的 物质，如铁、钴、镍等。
在磁场中具有反铁磁性 的物质，如锰、铬等。
02
磁场对磁介质的影响
磁场对磁介质的作用
磁化现象
磁场对磁介质产生作用，使其内 部磁矩定向排列，形成磁化现象。
剩余磁化强度
当磁场去除后，磁介质仍会保留一部分磁化强度， 称为剩余磁化强度。
磁介质的磁导率
相对磁导率
描述磁介质在磁场中的导磁能力与真空导磁能 力的比值。
最大磁导率
在一定磁场强度下，磁介质的磁导率达到最大 值。
温度系数
表示磁导率随温度变化的系数，某些材料的温度系数较大，对温度变化较为敏 感。
03
磁介质的性质与特点
磁滞现象
磁介质在磁化过程中会出现滞后现 象，即当磁场反向时，磁介质的磁 化强度不会立即消失，而是逐渐减 小。
磁损耗
在交变磁场中，磁介质会因为磁滞 现象和涡流效应产生能量损耗。
磁介质的磁化过程
起始磁化
磁介质在磁场中开始被磁化的过程，起始磁化曲 线通常是非线性的。
磁饱和
随着磁场强度的增加，磁介质的磁化强度逐渐达 到饱和状态，此时磁导率不再变化。
3
磁滞损耗
由于磁滞现象产生的能量损耗，通常表现为热量。
磁介质的损耗特性
介电损耗
01
由于电场作用在磁介质上产生的能量损耗，通常表现为热量。
涡流损耗
02
由于磁场变化产生的涡旋电流在磁介质中产生的能量损耗，通
常表现为热量。

7-9磁场中的磁介质

7-9磁场中的磁介质

磁介质 磁化 磁介质的分类： 一、磁介质的分类： 电介质的极化 电介质的极化
E
'
磁介质的磁化 磁介质的磁化
B0
r = 1 + χm
B0
+ +
E0
B'
or
B'
B r = B0
'
E = E0 + E' E < E0
B = B0 + B' B > B0
B = B0 + B B < B0
= 0r
r > 1 锰、铬、铝、氧、氮 … 顺磁质： 顺磁质：B>B0 抗磁质：B<B0 r < 1 金、银、铜、铋、锑、氢… 镍等合金。 铁磁质： 铁磁质：B>>B0 r >> 1 铁、钴、镍等合金。 注意： 真空: 注意： 10 真空 B=B0 ，r=1 χm = 0 。 20 顺： χm > 0 抗： χm < 0 超导： χm = 1 ， ，超导：
高磁导率， 高磁导率， 计算机中的记忆元件；电子 矩磁材料 高电阻率。 高电阻率。 技术中的天线和电感中磁心
B
B
O
H
O
H
O
H
软磁材料
硬磁材料
矩磁铁氧体材料
小 结 名称 特点 应用
相对磁导率 和饱和磁感 电磁铁、变压器、交流电动 软磁材料 强度较大， 强度较大， 机、交流发电机中的铁心。 矫顽力小。 矫顽力小。 剩磁和矫顽 硬磁材料 力都比较大。 力都比较大。 压磁材料 磁致伸缩 适于制造永磁体 探测海洋深度和鱼群
r
介质中磁导率。 介质中磁导率。
相对磁导率。 B 相对磁导率。 0 χm : 磁化率 r = 1 + χm 本节主要讨论磁介质对磁场的影响：从微观结构出发, 本节主要讨论磁介质对磁场的影响：从微观结构出发 分析磁介质的磁性起源，简单介绍磁化规律。 分析磁介质的磁性起源，简单介绍磁化规律。

磁场中的磁介质

磁场中的磁介质

2 . 磁化曲线（ H—B曲线）
（1）弱磁质（顺磁质、 （2）铁磁质， r 是变量。
抗磁质）， r 为常量。
B H—B曲线斜率： tg 0 r H
Bm是饱和磁感应强度
3. 铁磁向顺磁质的转化 当温度达到一定时，铁磁质转变为顺磁质。 这一温度被称为“居里点”。
二、铁磁质的磁化过程与磁滞回线
dt
B
pm
L
p m M
L
进动附加的进动角动量 L 是与 B0 的方向一致的。与这一进
动相应的磁矩 p m ，称感应磁矩，它是 B0 与反向的。 反向磁矩对应的磁场使介质内 B B B B 0 0 部磁场减弱。 虽然顺磁质分子也会产生感应磁矩,但由于它远小于 固有磁矩（相差五个数量级）,所以顺磁质中主要是固有 磁矩起作用。
B0
I
I
B
I
I
B r B0
r ……该磁介质的相对磁导率
磁介质的分类
铝
2 磁介质磁化的微观机制 分子磁矩 分子是一个复杂的带电系统。原子 Pm 中电子参与两种运动：自旋及绕核 i 的轨道运动，对应有轨道磁矩和自 旋磁矩。一个分子对应一个等效电 S 流i , 相应有一个 分子等效磁矩。 pm 是各个的电子轨道磁矩、电子 p m is 自旋磁矩、原子核磁矩的总和。 分子电流所对应的磁矩在外磁场中的行为决定介质 的特性。
顺磁质 : B B0 B B0
抗磁质 : B B0 B B0
磁化电流
' B B0 B
2. 磁化强度与磁化电流
（1）磁化强度
Σpm
M=
Σ pm +Σ Δ pm

大学物理恒定磁场中的磁介质解读

大学物理恒定磁场中的磁介质解读
B
Br
Hc
b
f o Hc
a
c e
H
Br
d
铁磁质中μ 随H 的变化曲线
磁滞回线
二、铁磁质的分类 铁 磁 质 矩磁材料 1）软磁材料 —— 磁滞回线窄、矫顽力小的材料。 软磁材料 硬磁材料
如电工纯铁、硅钢片，铁氧体等。广泛应用于变压器，互 感器，接触器，继电器等的铁心。
2）硬磁材料 —— 磁滞回线宽、矫顽力大的材料。
第十四章 恒定磁场中的磁介质
本章的主要内容
1、磁介质磁化及其微观本质。
2、磁场强度 H及磁介质中的安培环路定理。
3、铁磁质的主要特性及其应用。
§14.1 磁介质的磁化
一、分子电流 磁化强度 1、磁介质: 在磁场的作用下性质发生变化并影响原磁场分布 的物质。 轨道磁矩 磁效应 分子 电子 等效圆电流 总和 自旋磁矩
O
R
r
§14.3 铁磁质
一、铁磁质的磁化规律 铁磁质是磁化性能很强，是性能特异，用途广泛的磁介质。 主要有∶铁、钴、镍等金属和它们的某些化合物。 铁磁质的磁化规律可用实验方法研究。
如图将铁磁质做成环状，外部绕以线圈，通入电流， 铁磁质被磁化，副线圈接冲击电流计，可测环中的磁感应 强度。
磁场强度为： H
m 0 r 1
m 1
m , r 不是常数,
用于制造永磁铁、磁电式仪表，电声换能元件，永磁电机， 指南针等。
3）矩磁材料 —— 剩磁大的软磁材料。 可用作记忆元件，控制元件，开关元件。
三、磁畴 近代科学实验证明，铁磁质的磁性主要来源于电子自旋磁 矩。在无外磁场的时，铁磁质中电子自旋磁矩可以在小范围内 “自发地”排列起来，形成一个个小的“自发磁化区” — 磁 畴。 自发磁化的原因是由于 相邻原子中电子之间存在 着一种交换作用（一种量 子效应），使电子的磁矩 平行排列起来而达到自发 磁化的饱和状态 当存在外磁场时， 在外场的作用下磁畴的 取向与外磁场一致，显 现一定的磁性。

磁场中的磁介质

磁场中的磁介质
续增加时，B急剧地增加；到达点N后，再 增大H时，B的增加就比较缓慢了，呈现出 磁化饱和的程度。点P所对应的B值一般称为 饱和磁感应强度Bm，这时在铁磁质中，几乎 所有磁畴都已沿着外磁场B0方向排列。
实验表明，铁磁质的磁化曲线都是不可逆的。即达到饱和
后，如果逐渐减小电流I，B并不沿起始磁化曲线逆向地随H的 减小而减小，而是沿下图所示中另一条曲线PQ比较缓慢地减 小。这种B的变化落后于H的变化规律称为磁滞现象（简称磁 滞）。由于磁滞的缘故，当磁场强度H减小到零时，磁感应强 度B并不等于零，而是仍有一定的数值Br，Br称为剩余磁感应 强度（简称剩磁）。这时撤去线圈，铁磁质就是一块永磁体。
物理学
磁场中的磁介质
1.1 磁介质
磁介质是指在磁场作用下，其内部状态发生变化，并反过 来影响磁场存在和分布的物质。磁介质在磁场作用下内部状态 的变化称为磁化。
磁化了的磁介质会产生附加磁场，对原磁场产生影响。磁 介质在磁感应强度为B0的外磁场中，受外磁场的作用而被磁化 产生附加磁场B'。此时，在磁介质中的磁场B是这两个磁感应 强度的矢量和，即
2．磁化曲线与磁滞回线
铁磁质的特点是：① r 1 ，可达102～105数量级；② 相 对磁导率μr和磁导率μ会随着磁场强度H的变化而变化，即磁感 应强度B与磁场强度H不成线形关系。以上这些特点可以用B-H 曲线（也称磁化曲线）来描述。
B和H的关系可用实验测定。在实验中，可得出某一铁磁质 开始的B-H曲线，称为初始磁化曲线，如下图所示。从曲线可以 看出，当外加的磁场强度H从零逐渐增大时，可以看出介质的磁 感应强度B也逐渐增加；到达点M后，H继
顺磁质在没有外磁场时，磁介质中各分子磁矩的方向是杂 乱无章的。大量分子的磁矩相互抵消，所以宏观上磁介质不显 磁性。当有外电场B0时，所有分子磁矩都受到磁场力矩的作用 ，使各分子都不同程度地沿磁场方向排列，分子电流产生了一 个沿外磁场B0方向的附加磁场B'，从而使总的磁感应强度增加 ，即磁感应强度的值为B＝B0＋B'＞B0。

大学物理-磁场中的磁介质_图文_图文

大学物理-磁场中的磁介质_图文_图文

试 求（1）磁介质中任意点
I
P 的磁感应强度的大小；
（2）圆柱体外面一点Q
I
的磁感强度.
解
I I
同理可求
三 铁磁质
1 磁畴
有 外 磁 场
无外磁场
2 磁化曲线 磁滞回线
B/10-4T
15
ห้องสมุดไป่ตู้10
B=f (H)
5
θ
0
400
600 800 1 000 H/(Am-1)
顺磁质的B-H曲线
当外磁场由 逐渐减小时，这种 B 的变化落后于H的变 化的现象，叫做磁滞 现象 ，简称磁滞.
由于磁滞， 时，磁感强度 ， 叫做剩余磁感强 度(剩磁).
O
磁滞回线 矫顽力
3 铁磁性材料 不同铁磁性物质的磁滞回线形状相差很大.
O
O
O
软磁材料
硬磁材料 矩磁铁氧体材料
4 磁屏蔽
把磁导率不 同的两种磁介质 放到磁场中，在 它们的交界面上 磁场要发生突变 ，引起了磁感应 线的折射.
磁屏蔽示意图
大学物理-磁场中的磁介质_图文_图文.ppt
2 顺磁质和抗磁质的磁化 分子圆电流和磁矩
顺磁质的磁化
无外磁场
顺磁质内磁场
有外磁场
无外磁场时抗磁质分子磁矩为零
抗磁质的磁化
同向时
抗磁质内磁场
反向时
3 磁化强度
分子磁矩 的矢量和
体积元
单位:
意义 磁介质中单位体积内分子 的合磁矩.
二 磁介质中的安培环路定理
分子磁矩
C
（单位体积分子磁矩数
）
传导电流 分布电流
B
C
A
D
磁场强度

磁介质

磁介质

B~H r ~ H
16:58
H 23
3、磁滞回线
饱和磁感应强度 剩 磁
B
BS . Br . b
f . HC
a
初始磁 化曲线
矫顽力
HS
.
HC . c O
.
HS
磁滞回线
H
e . Br
d
16:58
BS
24
①磁化过程不可逆 磁滞回线--不可逆过程 H c B的变化落后于H，从而具有 剩磁，即磁滞效应。
Hc
B
Hc
H ②
r 大，易磁化，也易退磁
用途：适用于交变磁场中 电子设备中的各种电感元件、变压器、 镇流器，电动机和发电机中的铁芯等。 继电器、电磁铁的铁芯也用软磁材料。
16:58
纯铁，硅钢坡莫合金(Fe，Ni)，铁氧体等。
30
2、硬磁材料——作永久磁铁
B
Hc
矫顽力(Hc)大（>102A/m)，剩磁Br大 H c 磁滞回线的面积大，损耗大。
例1 一环形螺线管，管内充满磁导率为μ，相对磁导 率为μr的顺磁质。环的横截面半径远小于环的半径。 单位长度上的导线匝数为n。
求：环内的磁场强度和磁感应强度
解： H dl H 2r NI L
NI H nI 2r
r
O
B H 0 r H
16:58 13
SB dS 0 LH dl I 0 B H
21
12-3 铁磁质
一、铁磁质的磁化规律 1、铁磁质的特性 （1）能产生特别强的附加磁场 B ,使磁介质中的 B （2）铁磁质的磁导率 不是常量，B 与 H 不是线 性关系 （3） 磁化强度随外磁场而变，其变化落后于外磁 场的变化，而且在外磁场停止作用后，仍保 留部分磁性 （4）一定的铁磁材料存在一特定的临界温度—居 里点，当温度超过居里点时，铁磁质转变为 16:58 22 顺磁质。 远大于 B0 ,其 r B 值可达几百、甚至几千以上 0

磁场中的磁介质

磁场中的磁介质
§11-1 磁介质的磁化 磁化强度 11-
磁场中的磁介质 第十一 章 磁场中的磁介质
一.磁介质
v v v' B = B0 + B
真空中的 磁感强度 介质磁化后的 附加磁感强度
磁介质中的 总磁感强度 顺磁质 抗磁质 铁磁质
v v B > B0 v v B < B0
v v B >> B0
（铝、氧、锰等） 锰等） （铜、铋、氢等） 氢等） （铁、钴、镍等） 镍等）
R1 < r < R2
v v ∫ H dl = I
l
r
d
I
R2
I 2 π rH = I H= 2πr 0 r I B = H = 2πr
R1
磁场中的磁介质 第十一 章 磁场中的磁介质 §11-2. 磁介质中的安培环路定理、磁场强度 11磁介质中的安培环路定理、
R1 < r < R 2
I
B =
0 r I
弱磁质
§11-1 磁介质的磁化 磁化强度 11分子圆电流和磁矩
磁场中的磁介质 第十一 章 磁场中的磁介质
v m
I
B = B0 + B
'
顺 磁
Is
v B0
磁
无外磁场
有外磁场
§11-1 磁介质的磁化 磁化强度 11-
磁场中的磁介质 第十一 章 磁场中的磁介质
v 无外磁场时抗磁质分子磁矩为零 无外磁场时抗磁质分子磁矩为零 m = 0 v v B0 v' B0 v m 抗 ω 磁 v 质 q v v v q F 的 F v' v 磁 v' m v m v 化 v m' ω
H
O

大学物理课件-第12章磁场中的磁介质及磁场总结

大学物理课件-第12章磁场中的磁介质及磁场总结

单位：牛顿·米
5.电荷垂直于磁场作圆周运动的轨道半径
R
mv qB
6. 周期
T
2m
qB
7.螺距h ：电荷以任意角度进入磁场 作螺旋线运动
h 2mv cos
qB
8.霍尔电压
VH
RH
IB d
霍尔系数
RH
1 nq
1.毕奥--萨伐尔定律
电流元的磁场
dB
0 4
I
dl r r3
运动电荷的磁场
B
0 4
qv r r3
（A）相同 （B）不相同 （C）不确定
答案：[ A ]
B 0nI
练习2 通有电流 I 的单匝环型线圈，将其
弯成 N = 2 的两匝环型线圈，导线长度 和电流不变，问：线圈中心 o 点的磁感 应强度 B 和磁矩 pm是原来的多少倍？
（A）4倍，1/4倍
（B）4倍，1/2倍
（C）2倍，1/4倍 （D）2倍，1/2倍
• 能产生非常强的附加磁场B´，甚至是外磁场
的千百倍，而且与外场同方向。 • 磁滞现象，B 的变化落后于H 的变化。
• B 和H 呈非线性关系， 不是一个恒量。 • 高 值。
铁磁质的分类：
磁滞回线细而窄，矫顽 力小。
磁滞损耗小，容易磁 化，容易退磁，适用 于交变磁场。如制造 电机，变压器等的铁 芯。
第12章 磁场中的磁介质 12.1 磁介质对磁场的影响 12.2 原子的磁矩 12.3 磁介质的磁化 12.4 H的环路定理 12.5 铁磁质
12.1-12.3 磁介质及其分类 一、磁介质
物质的磁性
当一块介质放在外磁场中将会与磁场 发生相互作用，产生一种所谓的“磁化” 现象，介质中出现附加磁场。我们把这种 在磁场作用下磁性发生变化的介质称为 “磁介质”。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

§13-4磁场中的磁介质
在磁场中的磁介质要和磁场发生相互作用，结果也会使磁介质和磁场发生相应的改变。

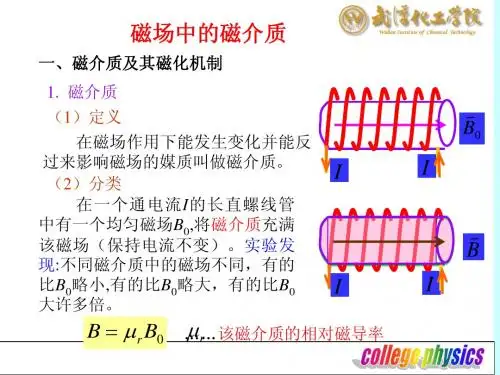
一、磁介质及其磁化机制
1．磁介质
所谓磁介质，是指在考虑物质受磁场的影响或它对磁场的影响时，我们把它们统称为磁介质(magnetic medium)
一个小圆电流所产生的磁场或它受磁场的作用都可以用它的磁偶极
矩（简称磁矩）来说明。

以I表示电流，S表示圆面积，则一个圆电流的磁矩为
下面我们用一个简单的模型来估算原子内电子轨道运动的磁矩的大小。

假设电子在半径为r的圆周上以恒定的速率绕原子核运动。

电子轨
道运动的周期就是。

由于每个周期内通过轨道上任一截面的电量为一个电子的电量e，
在一个分子中有许多电子和若干个核，一个分子的磁矩是其中所有电子的轨道磁矩和自旋磁矩以及核的自旋磁矩的矢量和。

有些分子在正常情况下，其磁矩的矢量和为零，由这些分子组成的物质称为抗磁质(diamagnetic medium)。

有些分子在正常情况下其磁矩的矢量和不为零，而是具有一定的值，这个值叫做分子的固有磁矩。

由这些分子组成的物质称为顺磁质
(paramagnetic medium )。

2．磁介质磁
化的微观机制
（1）进动与
附加磁矩
将物质放入
一外磁场0中，
在外磁场作用下，
电子的轨道磁矩
和自旋磁矩以及
原子核的自旋磁
矩都要受到磁力
矩的作用。

可以证明：不
论电子原来的磁
矩与磁场方向之
间的夹角是何值，在磁场0中，角动量进动的转向总是和0的方向满足右手螺旋关系。

电子的进动也相当于一个圆电流，因为电子带负电，这种等效电流的磁矩的方向永远与0的方向相反(图13-16a、b)。

因进动而产
生的等效电流的磁矩称为附加磁矩，用表示。

对电子及原子核的自旋，
外磁场也产生相同的效果。

因此，在外磁场的力矩作用下，一个分子内的所有电子和原子核都产生与外磁场方向相反的附加磁矩，这些附加磁矩的矢量和称为该分子在外磁场中所产生的感应磁矩(induced magnetic moment)。

感应磁矩的方向总是和外磁场的方向相反的。

[动画—电子进动]
（2）抗磁质的磁化
在抗磁质中，
每个原子或分子
中所有电子的轨
道磁矩和自旋磁
矩以及原子核的自旋磁矩的矢量和等于零（图13-17a、b）。

在外磁场0中每个分子都要产生一个感应磁矩，且外磁场越强，所产生的感应磁矩越大。

由于感应磁矩要激发一个附加磁场，其方向与外磁场方向相反（这种现象称为抗磁质的磁化），它对外磁场起着抵消的作用，所以抗磁质磁化后使磁介质中的磁场稍小于0。

（3）顺磁质
的磁化
顺磁质分子
具有固有磁矩，
在通常情况下，
由于分子热运动，
各个分子固有磁
矩的方向无规则排列（图13-18 a、b），其磁作用相互抵消，所以整个顺磁质物体不显示磁性。

当顺磁质放入磁场中时，其分子固有磁矩就要受到磁场的力矩的作用。

这力矩力图使分子的磁矩的方向转向与外磁场方向一致，当然分子的热运动会使各个分子的磁矩的这种取向不可能完全整齐。

外磁场越强，温度越低，分子磁矩的排列也越整齐，这些排列较整齐的分子磁矩要产生一个与外磁场同方向的附加磁场，这种现象称为顺磁质的磁化。

所以顺磁质对外磁场起着增强的作用。

也就是说顺磁质磁化后使磁介质中的磁场大
于0。

二、磁介质的磁
化规律
1．磁化电流
根据上面的
讨论，一块均匀
顺磁质放到外磁
场中时，它的分
子的固有磁矩要
沿着磁场方向取
向。

一块均匀抗
磁质放到外磁场中时，它的分子要产生感应磁矩。

考虑和这些磁矩相对应的小圆电流，可以发现在磁介质内部各处总是有相反的电流流过，它们的
磁作用相互抵消了。

但在磁介质表面上，这些小圆电流的外面部分未被抵消，它们都沿着相同的方向流动，这些表面上的小圆电流的总效果相当于在磁介质表面上有一层电流流过。

这种电流叫磁化电流(magnetization current)，也叫束缚电流(dound current)。

其面电流密度用j表示。

磁化电流是分子内的电荷运动一段段接合而成的，不同于导体中自由电荷定向移动而形成的传导电流，相比之下，导体中的传导电流可称作自由电流(free current)。

一块非均匀的磁介质放入磁场中时，除了在其表面要形成面磁化电流之外，在其内部还可以产生体磁化电流。

由于顺磁质分子的固有磁矩在磁场中的定向排列或抗磁质分子在磁场中产生了感应磁矩，因而在磁介质的内部或表面上出现磁化电流的现象叫做磁介质的磁化。

顺磁质的磁化电流的方向与磁介质中外磁场的方向满足右手螺旋关系，它产生的磁场要加强磁介质中的磁（图13-19a），抗磁质的磁化电流的方向与磁介质中外磁场的方向满足左手螺旋关系，它产生的磁场要减弱磁介质中的磁场（图13-19 b）。

这就是两种磁介质对磁场影响不同的原因。

[动画—磁化电流的形成]
2．磁介质中磁场
将磁介质放到磁场中时，由于磁场的作用，在磁介质中要出现磁化电流，而磁化电流产生的附加磁场反过来又影响磁场的分布。

这样，磁介质中的磁场就可以写成
式中0是真空中的磁场的磁感应强度，它可当作是某一自由电流所激发的；是磁化了的磁介质所激发的附加磁感应强度。

对于各向同性顺磁质，与0方向相同，B＞B0；对于各向同性抗磁质，与0方向相反，B ＜B0；而对于铁磁质来讲，B＞＞B0。

3．磁化强度
磁介质磁化后，在一个小体积元 V内的各个分子的磁矩的矢量和都将不等于零。

顺磁质分子的固有磁矩排列得越整齐，它们的矢量和就越大。

抗磁质分子所产生的感应磁矩越大，它们的矢量和也越大。

因此可以用单位体积内分子磁矩的矢量和来表示磁介质磁化的程度。

单位体积内分子磁矩的矢量和就叫做磁介质的磁化强度(magnetization intensity)。

以
表示小体积元∆V内磁介质的所有分子的磁矩的矢量和，以表示磁化强度，则有
式中表示小体积元∆V内磁介质的某个分子的磁矩，对于顺磁质，
是指分子的固有磁矩；对于抗磁质，是指分子的感应磁矩。

实验证明在一般的实验条件下，各向同性的顺磁质或抗磁质（以及铁磁质在一定条件下）的磁化强度都和磁感应强度成正比，其关系可表示为
由于磁介质的磁化电流是磁介质磁化的结果，所以磁化电流与磁化强度之间一定存在某种定量关系。

考虑磁介质内部一长度元，它和磁场的方向之间的夹角为θ。

由
于磁化，分子磁矩要沿的方向排列，因而等效分子电流的平面将转到与
垂直的方向。

设每个分子的分子电流为i，它所环绕的圆周半径为r，则与铰链的（即套住的）分子电流的中心都将位于以为轴线、以πr2为底面积的斜柱体内。

以n表示单位体积内的分子数，则与铰链的总分子电流为
如果dI是磁介质表面上沿表面的一个长度元，则dI将表现为面磁化电流。

dI/dl称做面磁化电流密度，以j表示面磁化电流密度，则由（13.4.4）可得
即面磁化电流密度等于该表面处磁介质的磁化强度沿表面的分量。

当 =0，即磁化强度与表面平行时，j=M，磁化电流与垂直。

在磁介质内与任意闭合路径L铰链的（闭合路径L包围的）总磁化电流，它应等于与L上各长度元铰链的磁化电流的和，即
三、有磁介质时的安培环路定理——磁场强度
1．有磁介质时的安培环路定理
磁介质放入磁场中时，由于磁化在磁介质中要出现磁化电流，而空间中的磁场分布也会发生相应的改变。

但系统平衡后（磁介质磁化后），空间中的磁场还是稳恒磁场，所以第十一章所述的真空中稳恒磁场的基本规律可以推广到有磁介质时的情况中来。

首先磁场的高斯定理的形式与前相同，即
高斯定理表明：不管是在真空中，还是在磁介质中，磁感应强度通过任意闭合曲面的通量恒等于零。

也就是说磁场是无源场。

下面再来推导安培环路定理的推广形式。

为了能形象地表示出磁场中磁场强度的分布，类似于用磁感应线描述磁感应强度分布的方法，我们也可以引入线来描述磁场。

线与矢量的关系规定如下：线上任一点的切线方向和该点矢量的方向相同，线的密度（即在与矢量垂直的单位面积上通过的线数目）和该点的
矢量的大小相等。

从（13.4.10）式可见，在各向同性的均匀磁介质中，通过任何截面的磁感应线的数目是通过同一截面线的 倍。