第6章 粒子群优化算法讲解
- 格式:ppt
- 大小:2.39 MB
- 文档页数:35

第6章粒子群优化算法PSO算法的基本原理是通过模拟粒子在空间中的移动,从而找到最优解。
每个粒子代表一个可能的解,并根据自身的经验和群体的经验进行。
粒子的速度和位置的更新使用以下公式:v(t+1) = w * v(t) + c1 * rand( * (pbest - x(t)) + c2 *rand( * (gbest - x(t))x(t+1)=x(t)+v(t+1)其中,v(t)代表粒子的当前速度,x(t)代表粒子的当前位置,w是惯性权重,c1和c2是学习因子,rand(是一个0到1之间的随机数,pbest 是粒子自身的最佳位置,gbest是整个群体的最佳位置。
PSO算法的过程如下:1.初始化粒子的位置和速度。
2.计算每个粒子的适应度值。
3. 更新每个粒子的pbest和gbest。
4.根据公式更新每个粒子的速度和位置。
5.重复步骤2到4,直到达到终止条件。
PSO算法有几个重要的参数需要设置:-群体大小:确定PSO算法中粒子的数量。
较大的群体大小可以增加整个空间的探索能力,但也增加了计算复杂度。
-惯性权重:控制粒子速度变化的因素。
较大的惯性权重可以增加粒子的飞行距离,但可能导致过程陷入局部最优解。
-学习因子:用于调节个体经验和群体经验的权重。
c1用于调节个体经验的权重,c2用于调节群体经验的权重。
较大的学习因子可以增加粒子的探索能力,但也可能增加时间。
PSO算法的优点是简单、易实现,收敛速度较快,对于多维、非线性、离散等问题具有良好的适应性。
然而,PSO算法也存在一些缺点,如易陷入局部最优解、对参数的敏感性等。
总之,粒子群优化算法是一种基于群体智能的优化算法,在求解复杂问题方面具有出色的性能。
它的基本原理是通过模拟粒子的移动来最优解,利用个体经验和群体经验进行自适应。
PSO算法在多个领域都有成功的应用,可以帮助解决实际问题。



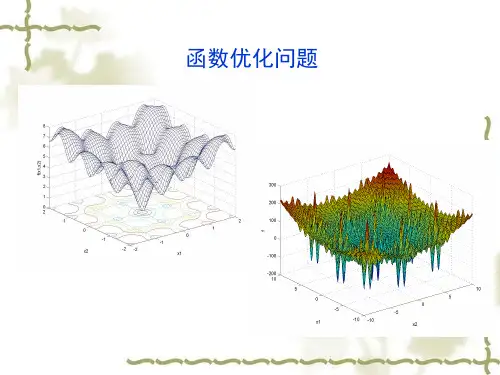




粒子群优化算法综述粒子群优化(Particle swarm optimization, PSO)是一种以群体行为模型为基础的进化算法,它是模拟群体中每个体的行动及各种影响机制来找到最优解。
1995年,Eberhart和Kennedy提出了粒子群优化(PSO)算法。
这个算法被用于多维、非线性优化问题,并认为其结果要好于其他搜索算法。
一、粒子群优化算法介绍:1、算法框架:粒子群优化算法是一种迭代搜索算法,它模拟生物世界中群体行为的进化机制来寻找最优解,它的基本框架如下:(1)初始化参数:决定搜索空间的边界条件,确定粒子群的初始状态;(2)计算适应度函数:按照不同的情况确定适应度函数,计算粒子群种群体的适应度;(3)更新种群体:根据当前种群体的适应度情况,更新个体的位置和速度;(4)迭代搜索:重复以上步骤,等待算法收敛到最优解;(5)结果输出:输出算法收敛的最优解。
2、算法特点:粒子群优化算法具有以下优势:(1)算法易于实现;(2)参数少;(3)计算局部搜索和全局搜索并重;(4)利用简单的几何形式,可以用于多目标优化问题。
二、应用情况:粒子群优化算法在多种复杂场景中应用十分灵活,它可以用于以下几个应用场景:(1)最优控制问题:用于解决轨道优化、多种自控问题。
(2)另一个应用领域是多元函数的优化求解,例如多元函数拟合、计算仿真等。
(3)另一个重要应用领域是信息处理,包括图像处理、模式识别等。
三、发展趋势:粒子群优化算法具有很好的搜索能力、实现简单以及参数少等优点,由于其交叉搜索能力和准确度,越来越受到关注,并被采用到各个领域。
然而,近些年,粒子群优化算法也因其原始算法难以改进收敛精度方面存在一定限制,受到两方面限制:一是获得最优解的能力较弱;二是收敛速度较慢。
四、结论:粒子群优化算法是一种利用生物行为模型进行优化的新算法,它在最优控制技术、多元函数优化求解以及信息处理等多个方面具有很好的应用价值。
虽然存在一定的缺点,但是随着计算机能力和计算机科学的发展,粒子群优化算法仍然具有良好的发展前景。


粒子群优化算法介绍
粒子群优化算法是一种基于群体智能的优化算法,它模拟了鸟群或鱼群等生物群体的行为,通过不断地迭代寻找最优解。
该算法最初由美国加州大学的Eberhart和Kennedy于1995年提出,目前已经被广泛应用于各种优化问题中。
粒子群优化算法的基本思想是将待优化问题转化为一个多维空间中的搜索问题,将每个解看作空间中的一个粒子,每个粒子的位置表示该解的参数值,速度表示该解的变化方向和速度。
在算法的每一次迭代中,每个粒子都会根据自身的历史最优解和群体最优解来更新自己的速度和位置,以期望找到更优的解。
具体来说,粒子群优化算法的实现过程如下:
1. 初始化粒子群,包括粒子的位置和速度等信息。
2. 计算每个粒子的适应度值,即待优化问题的目标函数值。
3. 更新每个粒子的速度和位置,包括考虑自身历史最优解和群体最优解的影响。
4. 判断是否满足停止条件,如果满足则输出最优解,否则返回第2步。
粒子群优化算法的优点在于其简单易懂、易于实现和收敛速度较快等特点。
同时,该算法还具有较好的全局搜索能力和鲁棒性,能够
应对复杂的非线性优化问题。
然而,粒子群优化算法也存在一些缺点,如易陷入局部最优解、对参数的选择较为敏感等问题。
因此,在实际应用中需要根据具体问题进行调整和优化。
粒子群优化算法是一种有效的优化算法,已经被广泛应用于各种领域,如机器学习、图像处理、控制系统等。
随着人工智能和大数据技术的不断发展,相信粒子群优化算法将会有更广泛的应用前景。