下载文档原格式
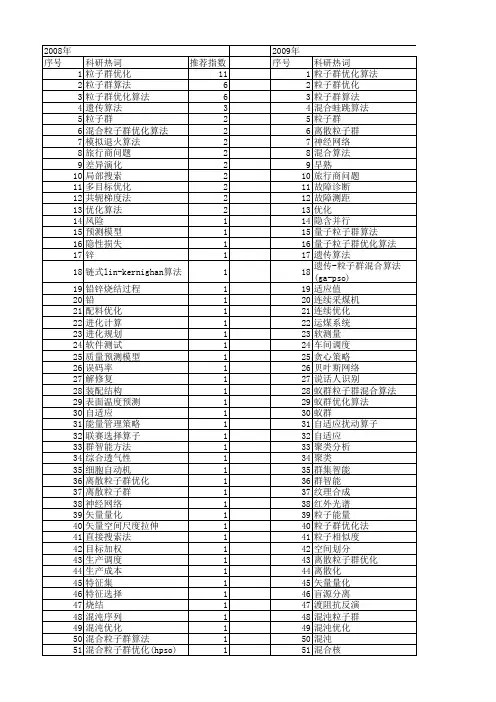
MATLAB 智能算法30个案例分析（终极版）1 基于遗传算法的TSP算法（王辉）2 基于遗传算法和非线性规划的函数寻优算法（史峰）3 基于遗传算法的BP神经网络优化算法（王辉）4 设菲尔德大学的MATLAB遗传算法工具箱（王辉）5 基于遗传算法的LQR控制优化算法（胡斐）6 遗传算法工具箱详解及应用（胡斐）7 多种群遗传算法的函数优化算法（王辉）8 基于量子遗传算法的函数寻优算法（王辉）9 多目标Pareto最优解搜索算法（胡斐）10 基于多目标Pareto的二维背包搜索算法（史峰）11 基于免疫算法的柔性车间调度算法（史峰）12 基于免疫算法的运输中心规划算法（史峰）13 基于粒子群算法的函数寻优算法（史峰）14 基于粒子群算法的PID控制优化算法（史峰）15 基于混合粒子群算法的TSP寻优算法（史峰）16 基于动态粒子群算法的动态环境寻优算法（史峰）17 粒子群算法工具箱（史峰）18 基于鱼群算法的函数寻优算法（王辉）19 基于模拟退火算法的TSP算法（王辉）20 基于遗传模拟退火算法的聚类算法（王辉）21 基于模拟退火算法的HEV能量管理策略参数优化（胡斐）22 蚁群算法的优化计算——旅行商问题（TSP）优化（郁磊）23 基于蚁群算法的二维路径规划算法（史峰）24 基于蚁群算法的三维路径规划算法（史峰）25 有导师学习神经网络的回归拟合——基于近红外光谱的汽油辛烷值预测（郁磊）26 有导师学习神经网络的分类——鸢尾花种类识别（郁磊）27 无导师学习神经网络的分类——矿井突水水源判别（郁磊）28 支持向量机的分类——基于乳腺组织电阻抗特性的乳腺癌诊断（郁磊）29 支持向量机的回归拟合——混凝土抗压强度预测（郁磊）30 极限学习机的回归拟合及分类——对比实验研究（郁磊）智能算法是我们在学习中经常遇到的算法，主要包括遗传算法，免疫算法，粒子群算法，神经网络等，智能算法对于很多人来说，既爱又恨，爱是因为熟练的掌握几种智能算法，能够很方便的解决我们的论坛问题，恨是因为智能算法感觉比较“玄乎”，很难理解，更难用它来解决问题。
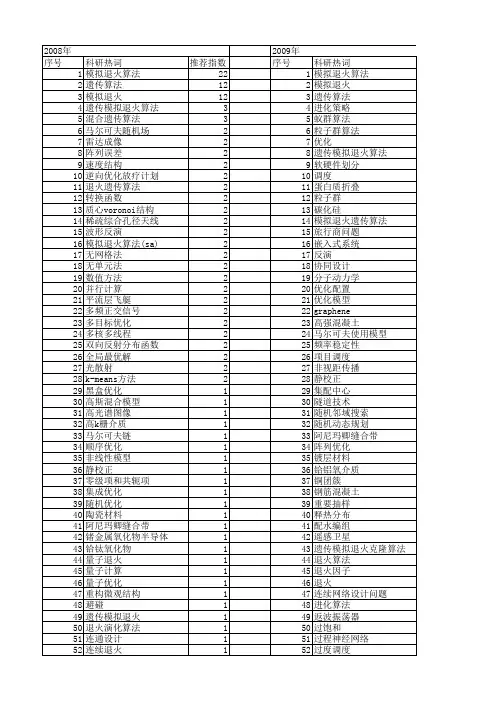
一种新混合粒子群算法及其在阵列天线方向图综合中的应用作者：姚旭曹祥玉陈沫来源：《现代电子技术》2008年第08期摘要：针对传统粒子群算法（PSO）中存在的易陷入局部最优解和后期收敛速度慢的问题，首次提出一种新混合粒子群算法（NHPSO），采用杂交粒子群算法和固定惯性权重策略，并把简化的二次插值法融入杂交粒子群算法中。
实验证明新算法大大提高了收敛速度，改善了解的质量。
对阵列天线特殊主瓣形式的波束赋形和旁瓣电平优化结果取得了非常好的效果，计算机仿真证实该新算法应用于此类问题非常有效。
关键词：粒子群算法；混合粒子群算法;二次插值法；阵列天线；波瓣赋形中图分类号：TN82文献标识码：B文章编号：1004-373X(2008)08-084-YAO Xu,CAO Xiangyu，(Laboratory of Microwave and Antennas Technology,Telecommunication College,Air ForceAbstract：A hybrid Particle Swarm Optimization(PSO) algorithm is proposed with fixed inertia weight in the hybrid particle swarm optimization algorithm,and a simplified quadratic interpolation method is integrated into this algorithm,aiming at overcoming easily trapping in the local extreme points and slow evolving speed of convergence.The experiment shows that this new algorithm improved the global search ability and the quality of optima.The results of both mainlobe shaping and sidelobe levels are very effective.The simulation results prove that the proposed hybrid new algorithm is efficieKeywords：particle swarm optimization algorithm;hybrid particle swarm optimization algorithm；quadratic interpolation method;array antennas;shaped beam在雷达、无线通信等众多领域中,常要求阵列天线具有确定的主瓣宽度、特殊形状的主瓣形状 (如余割波束、余割平方波束、扇形波束等)和低的副瓣电平。
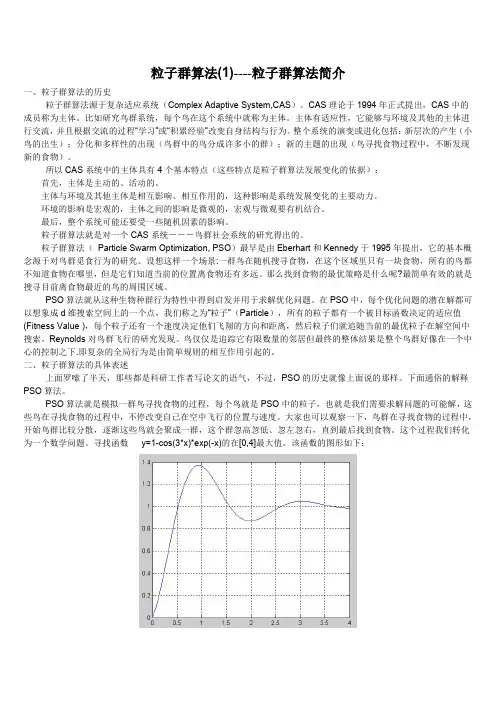
粒子群算法(1)----粒子群算法简介一、粒子群算法的历史粒子群算法源于复杂适应系统（Complex Adaptive System,CAS）。
CAS理论于1994年正式提出，CAS中的成员称为主体。
比如研究鸟群系统，每个鸟在这个系统中就称为主体。
主体有适应性，它能够与环境及其他的主体进行交流，并且根据交流的过程“学习”或“积累经验”改变自身结构与行为。
整个系统的演变或进化包括：新层次的产生（小鸟的出生）；分化和多样性的出现（鸟群中的鸟分成许多小的群）；新的主题的出现（鸟寻找食物过程中，不断发现新的食物）。
所以CAS系统中的主体具有4个基本特点（这些特点是粒子群算法发展变化的依据）：首先，主体是主动的、活动的。
主体与环境及其他主体是相互影响、相互作用的，这种影响是系统发展变化的主要动力。
环境的影响是宏观的，主体之间的影响是微观的，宏观与微观要有机结合。
最后，整个系统可能还要受一些随机因素的影响。
粒子群算法就是对一个CAS系统－－－鸟群社会系统的研究得出的。
粒子群算法（Particle Swarm Optimization,PSO）最早是由Eberhart和Kennedy于1995年提出，它的基本概念源于对鸟群觅食行为的研究。
设想这样一个场景:一群鸟在随机搜寻食物，在这个区域里只有一块食物，所有的鸟都不知道食物在哪里，但是它们知道当前的位置离食物还有多远。
那么找到食物的最优策略是什么呢?最简单有效的就是搜寻目前离食物最近的鸟的周围区域。
PSO算法就从这种生物种群行为特性中得到启发并用于求解优化问题。
在PSO中，每个优化问题的潜在解都可以想象成d维搜索空间上的一个点，我们称之为“粒子”（Particle），所有的粒子都有一个被目标函数决定的适应值(Fitness Value)，每个粒子还有一个速度决定他们飞翔的方向和距离，然后粒子们就追随当前的最优粒子在解空间中搜索。
Reynolds对鸟群飞行的研究发现。
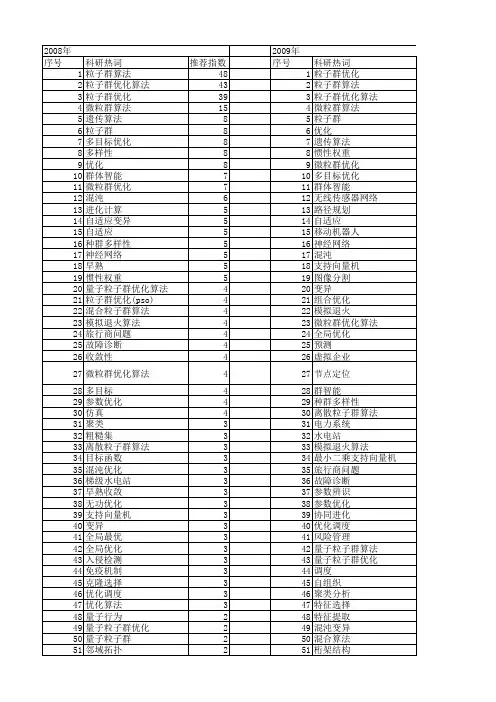
高效求解三维装箱问题的剩余空间最优化算法一、本文概述随着物流、制造业和计算机科学的快速发展，三维装箱问题（Three-Dimensional Bin Packing Problem, 3D-BPP）已成为一个备受关注的研究热点。
该问题涉及如何在有限的三维空间内，以最优的方式放置形状和大小各异的物体，以最大化空间利用率并减少浪费。
在实际应用中，如货物装载、仓库管理、集装箱运输等领域，高效求解三维装箱问题具有重大的经济价值和社会意义。
本文旨在研究三维装箱问题的剩余空间最优化算法，通过对现有算法的分析与改进，提出一种高效且实用的解决方案。
我们将对三维装箱问题进行详细定义和分类，阐述其在实际应用中的重要性和挑战性。
然后，我们将综述目前国内外在该领域的研究现状和进展，分析现有算法的优势和不足。
在此基础上，我们将提出一种基于启发式搜索和优化策略的剩余空间最优化算法，并通过实验验证其有效性和性能。
本文的主要贡献包括：1）对三维装箱问题进行系统性的分析和总结；2）提出一种新型的剩余空间最优化算法，以提高空间利用率和求解效率；3）通过实验验证所提算法的性能，并与其他先进算法进行比较和分析。
本文的研究成果将为三维装箱问题的求解提供新的思路和方法，有助于推动相关领域的理论研究和实际应用。
本文所提算法在实际应用中具有较高的推广价值，有望为物流、制造业等领域带来显著的经济效益和社会效益。
二、相关文献综述装箱问题，特别是三维装箱问题（3D Bin Packing Problem,3D-BPP），一直是计算机科学和运筹学领域研究的热点和难点。
随着物流、制造业等行业的快速发展，对装箱算法的效率和性能要求日益提高。
剩余空间最优化作为装箱问题中的一个重要目标，对于提高空间利用率、降低成本和减少浪费具有重要意义。
近年来，众多学者对三维装箱问题的剩余空间最优化算法进行了深入研究。
传统的启发式算法，如最先适应算法（First Fit）、最佳适应算法（Best Fit）和最差适应算法（Worst Fit）等，虽然简单直观，但在处理大规模或复杂装箱问题时往往效果不佳。
混合粒子群算法：基于模拟退火的算法
1. 算法原理
模拟退火算法在搜索过程中具有概率突跳的能力，能够有效地避免搜索过程中陷入局部
极小解。模拟退火算法在退火过程中不但接受好的解，而且还以一定的概率接受差得解，同
时这种概率受到温度参数的控制，其大小随温度的下降而减小。
2. 算法步骤
（1） 随机初始化种群中各微粒的位置和速度；
（2） 评价每个微粒的适应度，将当前各微子的位置和适应值存储在各微子的ip中，将所
有pbest的中适应最优个体的位置和适应值存储在gp中；
（3） 确定初始温度；
（4） 根据下式确定当前温度下各ip的适配值：
(()())/(()())/1()igigfpfptiNfpfptieTFpe
（5） 采用轮盘赌策略从所有ip中确定全局最优的某个替代值gp，然后根据下式更新各
微粒的速度和位置：
,,11,,22,,(1)()[()][()]ijijijijgjij
vtvtcrpxtcrpxt
,,,(1)()(1),1,2,...ijijij
xtxtvtjd
12
2
2
,24CccCCC
（6） 计算各微粒新的目标值，更新各微粒的ip值及群体的gp值；
（7） 进行退温操作；
（8） 若满足停止条件（通常为预设的运算精度或迭代次数），搜索停止，输出结果，否知
返回（4）继续搜索；
（9） 初始温度和退温温度对算法有一定的影响，一般采用如下的初温和退温方式：
10,()/ln5kkgtktfp
3. 算法MATLAB实现
在MATLAB中编程实现的基于杂交的粒子群算法优化函数为：SimuAPSO。
功能：用基于模拟退火的粒子群算法求解无约束优化问题。
调用格式：12[,](,,,,,,)xmfvSimuAPSOfitnessNcclamdaMD
其中，fitness：待优化的目标函数；
N
：粒子数目；
1
c
：学习因子1；
2
c
：学习因子2；
lamda
：退火常数；
M
：最大迭代次数；
D
：自变量的个数；
xm
：目标函数取最小值时的自变量值；
fv
：目标函数的最小值。
基于模拟退火的粒子群算法的MATLAB代码如下：
function [xm,fv]=SimuAPSO(fitness,N,c1,c2,lamda,M,D)
% fitness：待优化的目标函数;
% N：粒子数目;
% c1：学习因子1;
% c2：学习因子2;
% lamda:退火常数;
% M：最大迭代次数;
% D：自变量的个数;
% xm：目标函数取最小值时的自变量值;
% fv：目标函数的最小值。
format long;
for i=1:N
for j=1:D
x(i,j)=randn; %随机初始化位置
v(i,j)=randn; %随机初始化速度
end
end
for i=1:N
p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
pg=x(N,:); %pg为全局最优
for i=1:(N-1)
if fitness(x(i,:))
end
end
T=fitness(pg)/log(5); %初始温度
for t=1:M
groupFit=fitness(pg);
for i=1:N %当前温度下各个pi的适应值
Tfit(i)=exp(-(p(i)-groupFit)/T);
end
SumTfit=sum(Tfit);
Tfit=Tfit/SumTfit;
pBet=rand();
for i=1:N %用轮盘赌策略确定全局最优的某个替代值
ComFit(i)=sum(Tfit(1:i));
if pBet<=ComFit(i)
pg_plus=x(i,:);
break;
end
end
C=c1+c2;
ksi=2/abs(2-C-sqrt(C^2-4*C)); %速度压缩因子
for i=1:N
v(i,:)=ksi*(v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg_plus-x(i,:)));
x(i,:)=x(i,:)+v(i,:);
if fitness(x(i,:))
y(i,:)=x(i,:);
end
if p(i)
end
end
T=T*lamda;
end
xm=pg';
fv=fitness(pg);
例
基于模拟退火的粒子群算法应用实例。求下面函数的最小值
15211()0.01,1010,1,2,...51iiifxxiix
取粒子数目为40，学习因子都取2.05，迭代步数取10000，退火常数取为0.5。
解：
首先建立目标函数文件
.fitnessm
：
function F=fitness(x)
F=0;
for i=1:5
F=F+1/(i+(x(i)-1)^2);
end
F=1/(0.01+F);
在MATLAB命令窗口中输入：
>> [xm,fv]=SimuAPSO(@fitness,40,2.05,2.05,0.5,10000,5)
所得结果为：
xm =
0.999999992830566
0.999999968868289
1.000000045205848
0.999999990239291
0.999999963875179
fv =
0.436046511627907
从结果可以看出，基于模拟退火的粒子群算法求得的结果精度是非常高的。
