江苏专版2019届高三数学备考冲刺140分问题05应用三角函数的性质求解参数含解
- 格式:pdf
- 大小:510.36 KB
- 文档页数:17

问题5应用三角函数的性质求解参数问题一、考情分析利用三角函数的性质求参数取值或范围是往往是高考中的亮点,这类问题一般涉及到值域、单调性及周期性等性质,三角函数因为其函数性质的特殊性,如正弦函数和余弦函数的有界性,往往在确定变量范围,或者最大值最小值有关问题上起着特殊的作用.如果试题本身对自变量的取值范围还有限制,则更应该充分注意. 二、经验分享(1) 三角函数值域的不同求法 ①利用sin x 和cos x 的值域直接求;②把所给的三角函数式变换成y =A sin(ωx +φ)的形式求值域; ③通过换元,转换成二次函数求值域.(2)已知三角函数解析式求单调区间:①求函数的单调区间应遵循简单化原则,将解析式先化简,并注意复合函数单调性规律“同增异减”;②求形如y =A sin(ωx +φ)或y =A cos(ωx +φ)(其中ω>0)的单调区间时,要视“ωx +φ”为一个整体,通过解不等式求解.但如果ω<0,那么一定先借助诱导公式将ω化为正数,防止把单调性弄错.(3)已知三角函数的单调区间求参数.先求出函数的单调区间,然后利用集合间的关系求解. (4)对于函数y =A sin(ωx +φ),其对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点,因此在判断直线x =x 0或点(x 0,0)是不是函数的对称轴或对称中心时,可通过检验f (x 0)的值进行判断.(5)求三角函数周期的方法: ①利用周期函数的定义.②利用公式:y =A sin(ωx +φ)和y =A cos(ωx +φ)的最小正周期为2π|ω|,y =tan(ωx +φ)的最小正周期为π|ω|.(6)图象变换:由函数y =sin x 的图象通过变换得到y =A sin(ωx +φ)的图象,有两种主要途径:“先平移后伸缩”与“先伸缩后平移”.(8)求y =A sin(ωx +φ)+B (A >0,ω>0)解析式的步骤①求A ,B ,确定函数的最大值M 和最小值m ,则A =M -m2,B =M +m2.②求ω,确定函数的周期T ,则ω=2πT .③求φ,常用方法如下:i.代入法:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入.ii.五点法:确定φ值时,往往以寻找“五点法”中的特殊点作为突破口.具体如下:“第一点”(即图象上升时与x 轴的交点)为ωx +φ=0;“第二点”(即图象的“峰点”)为ωx +φ=π2;“第三点”(即图象下降时与x 轴的交点)为ωx +φ=π;“第四点”(即图象的“谷点”)为ωx +φ=3π2;“第五点”为ωx +φ=2π. 三、知识拓展 1.对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是14个周期.(2)正切曲线相邻两对称中心之间的距离是半个周期. 2.奇偶性若f (x )=A sin(ωx +φ)(A ,ω≠0),则(1)f (x )为偶函数的充要条件是φ=π2+k π(k ∈Z ); (2)f (x )为奇函数的充要条件是φ=k π(k ∈Z ).3.由y =sin ωx 到y =sin(ωx +φ)(ω>0,φ>0)的变换:向左平移φω个单位长度而非φ个单位长度.4.函数y =A sin(ωx +φ)的对称轴由ωx +φ=k π+π2,k ∈Z 确定;对称中心由ωx +φ=k π,k ∈Z 确定其横坐标. 四、题型分析(一) 与函数最值相关的问题 【例1】已知函数.(1)求函数()f x 的最小正周期与单调递增区间; (2)若时,函数()f x 的最大值为0,求实数m 的值.【分析】(1)()f x 化为,可得周期22T ππ==,由可得单调递增区间;(2)因为,所以,进而()f x 的最大值为,解得12m =.【解析】(1),则函数()f x 的最小正周期T π=, 根据,k Z ∈,得,k Z ∈,所以函数()f x 的单调递增区间为,k Z ∈.(2)因为,所以,则当262x ππ-=,3x π=时,函数取得最大值0, 即,解得12m =. 【点评】三角函数的最值问题,大多是含有三角函数的复合函数最值问题,常用的方法为:化为代数函数的最值,也可以通过三角恒等变形化为求y =A sin(ωx +φ)+B 的最值;或化为关于sin x (或cos x )的二次函数式,再利用换元、配方等方法转化为二次函数在限定区间上的最值. 【小试牛刀】【江苏省启东中学2018届高三上学期第二次月考】若方程在[)0,2π上有且只有两解,则实数m 的取值范围_____.【答案】【解析】所以当时, y m = 与22y t t =+ 只有一个交点,当3m =时1t =,方程解所以要使方程在[)0,2π上有且只有两解,实数m 的取值范围(二) 根据函数单调性求参数取值范围如果解析式中含有参数,要求根据函数单调性求参数取值范围,通常先求出函数的单调区间,然后利用集合间的关系求解.或转化为使得某个等式或不等式(可以、恒)成立,通常分离参数,求出解析式的范围或最值,进而求出参数的范围即可.【例2】已知ω>0,函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π4在⎝ ⎛⎭⎪⎫π2,π上单调递减,则ω的取值范围是________. 【分析】根据y =sin x 在⎝ ⎛⎭⎪⎫π2,3π2上递减,列出关于ω的不等式组【解析】 由π2<x <π,ω>0得,ωπ2+π4<ωx +π4<ωπ+π4, 又y =sin x 在⎝ ⎛⎭⎪⎫π2,3π2上递减,所以⎩⎪⎨⎪⎧ωπ2+π4≥π2,ωπ+π4≤3π2,解得12≤ω≤54.【答案】⎣⎢⎡⎦⎥⎤12,54【点评】求函数的单调区间应遵循简单化原则,将解析式先化简,并注意复合函数单调性规律“同增异减”;求形如y =A sin(ωx +φ)或y =A cos(ωx +φ)(其中ω>0)的单调区间时,要视“ωx +φ”为一个整体,通过解不等式求解.但如果ω<0,那么一定先借助诱导公式将ω化为正数,防止把单调性弄错;已知三角函数的单调区间求参数.先求出函数的单调区间,然后利用集合间的关系求解.【小试牛刀】【南京市、盐城市2018届高三年级第一次模拟】若函数sin y x ω=在区间[]0,2π上单调递增,则实数ω的取值范围是________.【答案】10,4⎛⎤ ⎥⎝⎦【解析】由题意得,所以5.(三) 根据函数图象的对称性求参数取值范围 【例3】已知函数.(1)若函数)(x f y =的图像关于直线对称,求a 的最小值;(2)若存在使成立,求实数m 的取值范围.【分析】(1)先利用降幂公式进行化简,然后利用辅助角公式将)(x f 化为,最后根据正弦函数的对称性求出对称轴,求出a 的最小值即可; (2)根据的范围求出320π+x 的范围,再结合正弦函数单调性求出函数f (x 0)的值域,从而可求出m =00021()20()sin(2)3mf x m f x x π-=⇒==+的取值范围.【解析】(1)首先将函数)(x f y =的解析式化简为:,又因为函数)(x f y =的图像关于直线对称,所以,即,又因为0>a ,所以a 的最小值为12π. (2)故.【点评】对于函数y =A sin(ωx +φ),其对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点,因此在判断直线x =x 0或点(x 0,0)是不是函数的对称轴或对称中心时,可通过检验f (x 0)的值进行判断.【小试牛刀】【2018届安徽省亳州市蒙城高三第五次月考】若将函数的图象向左平移()0ϕϕ>个单位,所得的图象关于y 轴对称,则ϕ的最小值是 【答案】8π【解析】函数的图象向左平移()0ϕϕ>个单位,得到图象关于y 轴对称,即,解得,又0ϕ>,当0k =时, ϕ的最小值为8π. (四) 等式或不等式恒成立问题在等式或不等式恒成立问题中,通常含有参数,而与三角函数相关的恒成立问题,一定要注意三角函数自身的有界性,结合自变量的取值范围,才能准确求出参数的取值或范围. 【例4】已知不等式对于,33x ππ⎡⎤∈-⎢⎥⎣⎦恒成立,则实数m 的取值范围是 【答案】22m ≤【解析】因为=,所以原不等式等价于在,33x ππ⎡⎤∈-⎢⎥⎣⎦恒成立.因为,所以∈22]2,所以22m ≤,故选B . 【点评】解决恒成立问题的关键是将其进行等价转化,使之转化为函数的最值问题,或者区间上的最值问题,使问题得到解决.具体转化思路为:若不等式()f x A >在区间D 上恒成立,则等价于在区间D 上()f x 的最小值大于A ;若不等式()f x B <在区间D 上恒成立,则等价于在区间D 上()f x 最大值小于B .【小试牛刀】【2018届江苏省常熟市高三上学期期中】已知函数,若对任意的实数,都存在唯一的实数[]0,m β∈,使,则实数m 的最小值是__________. 【答案】2π【解析】函数,若对任意的实数,则:f (α)∈[3由于使f (α)+f (β)=0,则:f (β)∈3].,,β=2π,所以:实数m 的最小值是2π.故答案为: 2π(五) 利用三角代换解决范围或最值问题由于三角函数的有界性,往往可以用它们来替换一些有范围限制的变量,再利用三角函数的公式进行变换,得到新的范围,达到解决问题的目的.【例5】已知12,F F 是椭圆和双曲线的公共焦点,P 是他们的一个公共点,且,则椭圆和双曲线的离心率的倒数之和的最大值为__________.A .33 B .33C .3D .2 【解析】设椭圆方程为22221x y a b+=(a >b >0),双曲线方程为222211x y a b -=(a >0,b >0),其中a >a 1,半焦距为c ,于是|PF 1|+|PF 2|=2a ,|PF 1|-|PF 2|=2a 1, 即|PF 1|=a +a 1,|PF 2|=a -a 1, 因为,由余弦定理:4c 2=(a +a 1)2+(a -a 1)2-2(a +a 1)(a -a 1)即4c 2=a 2+3a 12,即令ac =2cos θ13a c=2sin θ 所以【点评】合理使用三角代换,可以使得运算步骤(特别是与求最值相关的运算)变得非常简洁.【小试牛刀】已知实数,x y 满足221x y +=,则的最小值为【答案】43【解析】由221x y +=,可设,则=.五、迁移运用1.【江苏省常州市2019届高三上学期期末】已知函数是偶函数,点是函数图象的对称中心,则最小值为________.【答案】【解析】∵函数f (x )=sin (ωx +φ)(ω>0,φ∈R )是偶函数, ∴φ=,∵点(1,0)是函数y =f (x )图象的对称中心 ∴sin (ω+φ)=0,可得ω+φ=k 2π,k 2∈Z , ∴ω=k 2π﹣φ=(k 2﹣k 1)π﹣.又ω>0,所以当k 2﹣k 1=1时,ω的最小值为. 故答案为:.2.【江苏省盐城市、南京市2019届高三年级第一次模拟】设函数,其中.若函数在上恰有个零点,则的取值范围是________.【答案】【解析】取零点时满足条件,当时的零点从小到大依次为,所以满足 ,解得:3.【江苏省苏北四市2019届高三第一学期期末】将函数()的图象向左平移个单位长度后,所得图象关于直线对称,则的最小值为______.【答案】【解析】将函数f(x)=sin(ωx)(ω>0)的图象向左平移个单位后,可得函数y=sin(ωx)的图象,再根据所得图象关于直线x=π对称,可得ωπkπ,k ∈Z,∴当k=0时,ω取得最小值为,故答案为:.4.【江苏省徐州市2019届高三上学期期中】已知函数,若,且,则的最大值为______.【答案】【解析】令=1,,则,===,m,n,k都是整数,因为,所以,所以,的最大值为.5.【江苏省常州2018届高三上学期期末】如图,在平面直角坐标系xOy中,函数的图像与x 轴的交点A , B , C 满足,则ϕ=________.【答案】34π 【解析】不妨设0x ωϕ+=, πx ωϕ+=,,得,由,得,解得3π4ϕ=. 6.【江苏省淮安市等四市2018届高三上学期第一次模拟】若函数的图象与直线y m =的三个相邻交点的横坐标分别是6π, 3π, 23π,则实数ω的值为____. 【答案】4 【解析】,所以4ω=。

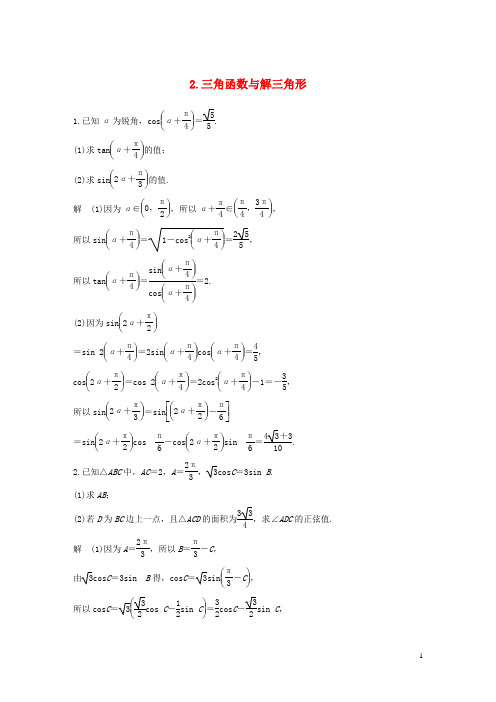
2.三角函数与解三角形1.已知α为锐角,cos ⎝ ⎛⎭⎪⎫α+π4=55. (1)求tan ⎝ ⎛⎭⎪⎫α+π4的值;(2)求sin ⎝⎛⎭⎪⎫2α+π3的值. 解 (1)因为α∈⎝ ⎛⎭⎪⎫0,π2,所以α+π4∈⎝ ⎛⎭⎪⎫π4,3π4,所以sin ⎝⎛⎭⎪⎫α+π4=1-cos 2⎝⎛⎭⎪⎫α+π4=255,所以tan ⎝ ⎛⎭⎪⎫α+π4=sin ⎝ ⎛⎭⎪⎫α+π4cos ⎝ ⎛⎭⎪⎫α+π4=2.(2)因为sin ⎝⎛⎭⎪⎫2α+π2=sin 2⎝ ⎛⎭⎪⎫α+π4=2sin ⎝ ⎛⎭⎪⎫α+π4cos ⎝ ⎛⎭⎪⎫α+π4=45, cos ⎝ ⎛⎭⎪⎫2α+π2=cos 2⎝ ⎛⎭⎪⎫α+π4=2cos 2⎝ ⎛⎭⎪⎫α+π4-1=-35, 所以sin ⎝ ⎛⎭⎪⎫2α+π3=sin ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫2α+π2-π6=sin ⎝ ⎛⎭⎪⎫2α+π2cos π6-cos ⎝ ⎛⎭⎪⎫2α+π2sin π6=43+310.2.已知△ABC 中,AC =2,A =2π3,3cos C =3sin B .(1)求AB ;(2)若D 为BC 边上一点,且△ACD 的面积为334,求∠ADC 的正弦值.解 (1)因为A =2π3,所以B =π3-C ,由3cos C =3sin B 得,cos C =3sin ⎝ ⎛⎭⎪⎫π3-C ,所以cos C =3⎝⎛⎭⎪⎫32cos C -12sin C =32cos C -32sin C ,所以12cos C =32sin C ,即tan C =33.又因为C ∈⎝⎛⎭⎪⎫0,π3,所以C =π6,从而得B =π3-C =π6,所以AB =AC =2.(2)由已知得12·AC ·CD sin π6=334,所以CD =332,在△ACD 中,由余弦定理得,AD 2=AC 2+CD 2-2AC ·CD cos C =74,即AD =72, 由正弦定理得,ADsin C =ACsin∠ADC ,故sin∠ADC =AC sin C AD =277. 3.已知函数f (x )=A sin ⎝ ⎛⎭⎪⎫ωx +π3(A >0,ω>0)图象的相邻两条对称轴之间的距离为π,且经过点⎝⎛⎭⎪⎫π3,32. (1)求函数f (x )的解析式;(2)若角α满足f (α)+3f ⎝ ⎛⎭⎪⎫α-π2=1,α∈(0,π),求角α的值. 解 (1)由条件知周期T =2π, 即2πω=2π,所以ω=1,即f (x )=A sin ⎝⎛⎭⎪⎫x +π3.因为f (x )的图象经过点⎝ ⎛⎭⎪⎫π3,32,所以A sin 2π3=32,所以A =1,所以f (x )=sin ⎝⎛⎭⎪⎫x +π3.(2)由f (α)+3f ⎝ ⎛⎭⎪⎫α-π2=1,得sin ⎝ ⎛⎭⎪⎫α+π3+3sin ⎝ ⎛⎭⎪⎫α+π3-π2=1,即sin ⎝ ⎛⎭⎪⎫α+π3-3cos ⎝⎛⎭⎪⎫α+π3=1,所以2sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α+π3-π3=1, 即sin α=12.因为α∈(0,π),所以α=π6或5π6.4.在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且b sin 2C =c sin B . (1)求角C 的大小;(2)若sin ⎝⎛⎭⎪⎫B -π3=35,求sin A 的值.解 (1)由b sin 2C =c sin B ,根据正弦定理得 2sin B sin C cos C =sin C sin B .因为sin B >0,sin C >0,所以cos C =12.又C ∈(0,π),所以C =π3.(2)因为C =π3,所以B ∈⎝ ⎛⎭⎪⎫0,2π3,所以B -π3∈⎝ ⎛⎭⎪⎫-π3,π3,又sin ⎝ ⎛⎭⎪⎫B -π3=35,所以cos ⎝⎛⎭⎪⎫B -π3=1-sin 2⎝⎛⎭⎪⎫B -π3=45.又A +B =2π3,即A =2π3-B ,所以sin A =sin ⎝ ⎛⎭⎪⎫2π3-B =sin ⎣⎢⎡⎦⎥⎤π3-⎝ ⎛⎭⎪⎫B -π3 =sin π3cos ⎝ ⎛⎭⎪⎫B -π3-cos π3sin ⎝⎛⎭⎪⎫B -π3=32×45-12×35=43-310. 5.已知向量a =(2cos α,sin 2α),b =(2sin α,t ),α∈⎝ ⎛⎭⎪⎫0,π2.(1)若a -b =⎝ ⎛⎭⎪⎫25,0,求t 的值;(2)若t =1,且a·b =1,求tan ⎝⎛⎭⎪⎫2α+π4的值.解 (1)方法一 因为向量a =(2cos α,sin 2α),b =(2sin α,t ),且a -b =⎝ ⎛⎭⎪⎫25,0,所以cos α-sin α=15,t =sin 2α.由cos α-sin α=15,得(cos α-sin α)2=125,即1-2sin αcos α=125,从而2sin αcos α=2425.所以(cos α+sin α)2=1+2sin αcos α=4925.因为α∈⎝⎛⎭⎪⎫0,π2,所以cos α+sin α=75,所以sin α=(cos α+sin α)-(cos α-sin α)2=35,从而t =sin 2α=925.方法二 因为向量a =(2cos α,sin 2α),b =(2sin α,t ), 且a -b =⎝ ⎛⎭⎪⎫25,0,所以cos α-sin α=15,t =sin 2α.又sin 2α+cos 2α=1,所以sin 2α+⎝ ⎛⎭⎪⎫sin α+152=1,整理得50sin 2α+10sin α-24=0, 解得sin α=-45或sin α=35.因为α∈⎝ ⎛⎭⎪⎫0,π2,所以sin α>0,所以sin α=35, 从而t =sin 2α=925.(2)方法一 因为t =1,且a·b =1,所以4sin αcos α+sin 2α=1,即4sin αcos α=cos 2α. 因为α∈⎝ ⎛⎭⎪⎫0,π2,所以cos α≠0,从而tan α=14.所以tan 2α=2tan α1-tan 2α=815. 从而tan ⎝⎛⎭⎪⎫2α+π4=tan 2α+tanπ41-tan 2α·tan π4=815+11-815=237.方法二 因为t =1,且a·b =1,所以4sin αcos α+sin 2α=1,即4sin αcos α=cos 2α. 所以2sin 2α=1+cos 2α2,即4sin 2α-cos 2α=1,又sin 22α+cos 22α=1,所以sin 22α+(4sin 2α-1)2=1, 整理得17sin 22α-8sin 2α=0, 解得sin 2α=817或sin 2α=0.因为α∈⎝⎛⎭⎪⎫0,π2,所以2α∈(0,π),所以sin 2α>0,所以sin 2α=817,代入4sin 2α-cos 2α=1,得cos 2α=1517,因为tan 2α=sin 2αcos 2α=815,从而tan ⎝⎛⎭⎪⎫2α+π4=tan 2α+tanπ41-tan 2α·tan π4=815+11-815=237.6.已知函数f (x )=23·sin 2⎝ ⎛⎭⎪⎫π4+x +2sin ⎝ ⎛⎭⎪⎫π4+x ·cos ⎝ ⎛⎭⎪⎫π4+x .(1)求函数f (x )的单调递增区间;(2)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且角A 满足f (A )=3+1,若a =3,BC 边上的中线长为3,求△ABC 的面积S .解 (1)f (x )=23sin 2⎝ ⎛⎭⎪⎫π4+x +2sin ⎝ ⎛⎭⎪⎫π4+x cos ⎝ ⎛⎭⎪⎫π4+x=3⎣⎢⎡⎦⎥⎤1-cos ⎝ ⎛⎭⎪⎫π2+2x +sin ⎝ ⎛⎭⎪⎫π2+2x=3sin 2x +cos 2x +3=2sin ⎝ ⎛⎭⎪⎫2x +π6+ 3.令-π2+2k π≤2x +π6≤π2+2k π,k ∈Z ,得-π3+k π≤x ≤π6+k π,k ∈Z ,所以函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤-π3+k π,π6+k π,k ∈Z .(2)由f (A )=2sin ⎝ ⎛⎭⎪⎫2A +π6+3=3+1,得sin ⎝⎛⎭⎪⎫2A +π6=12,因为A ∈(0,π),所以2A ∈(0,2π),2A +π6∈⎝ ⎛⎭⎪⎫π6,13π6,所以2A +π6=5π6,则A =π3,又BC 边上的中线长为3,所以|AC →+AB →|=6,所以|AC →|2+|AB →|2+2AC →·AB →=36,即b 2+c 2+2bc cos A =36,所以b 2+c 2+bc =36, ①由余弦定理a 2=b 2+c 2-2bc cos A , 得b 2+c 2-bc =9, ②由①②得,bc =272,所以S =12bc sin A =2738.。

江苏省2019年高三数学《三角函数》题型归纳(含解析)题型一:三角函数求值 (1)若1sin 34πα⎛⎫-=⎪⎝⎭,则cos 6πα⎛⎫+ ⎪⎝⎭=________. (2)已知2tan()3πα-=-,且(,)2παπ∈--,则cos()3sin()cos()9sin απαπαα-++-+=________. (3)已知()2tan =-απ,则ααααcos sin cos sin +-=________.(4)已知2)tan(-=-απ,则=+αα2cos 2cos 1________. (5)设α、β都是锐角,且cos α=13,sin (α+β)=45,则cos β=________. (6)设⎪⎭⎫⎝⎛∈⎪⎭⎫ ⎝⎛∈ππβπα,2,2,0,若()97sin ,31cos =+-=βαβ,则αsin =________.(7)若3cos()45πα-=,则sin 2α=________. (8)已知,022ππαπβ<<<<,3tan 4α=-,()5cos 13βα-=,则sin β的值为 . (9)已知错误!未找到引用源。
,且错误!未找到引用源。
,则cos α=________.(10)已知,αβ均为锐角,且cos()αβ+=sin()αβ-=2β=________. 答案:(1)14(2)15-(3)3 解析:()tan 2tan 2παα-=∴=- sin cos tan 1213sin cos tan 121αααααα----∴===++-+(4)25-解析:tan()tan 2παα-=-=-,则tan 2α=, 2222221sin cos cos 2cos cos sin cos ααααααα+=+-+2222tan 12152tan 222αα++===---(5 解析:由α是锐角及1cos 3α=知sin α=且3πα>,又β是锐角及4sin()5αβ+=,可得3cos()5αβ+=±,若3cos()5αβ+=,则αβ+为锐角,又4sin()5αβ+=<知3παβ+<,又3πα>,所以3παβ+>,与3παβ+<矛盾,3cos()5αβ+=-,可得[]cos cos ()βαβα=+-cos()cos sin()sin αβααβα=+++=314535-⋅+= (6)31(7)725- 解析:2237cos 22cos 12144525ππαα⎡⎤⎛⎫⎛⎫⎛⎫-=--=⋅-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ ,且cos 2cos 2sin 242ππααα⎡⎤⎛⎫⎡⎤-=-=⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦(8)6365解析:0-<<-αβπ,又因为()0135cos >=-αβ,所以02<-<-αβπ,()1312sin -=-αβ,因为43tan -=α,所以53sin =α,54cos -=α,而()[]()()6563131********sin cos cos sin sin sin =⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-+⨯=-+-=-+=αβααβααβαβ(9) 解析:由262cos 2sin =+αα得31sin 2α+=,所以1sin 2α=,因为),2(ππα∈,所以cos α=(10)4π解析:∵,αβ均为锐角,∴0αβπ<+<,∴sin()αβ+==,又∵22ππαβ-<-<,∴cos()αβ-==∴cos(2)cos[()()]βαβαβ=+--=+=∵β为锐角,∴02βπ<<,∴24πβ=.题型二:求三角函数的单调区间(1)已知函数1cos 222y x x =--,则函数函数的单调递增区间为______;单调递减区间为______.(2)将函数()()2sin 03f x x πωω⎛⎫=-> ⎪⎝⎭的图像向左平移3πω个单位,得到函数()y g x =的图像.若()y g x =在0,4π⎡⎤⎢⎥⎣⎦上为增函数,则ω的最大值为______.(3)已知函数),0)(62sin()(>+=ωπωx x f 直线21,x x x x ==是)(x f y =图像的任意两条对称轴,且21x x -的最小值为2π.则函数)(x f 的单调增区间为______.(4)函数sin 34y x π⎛⎫=-⎪⎝⎭的单调减区间为______. (5)函数()2cos tan xf x xsinx=的单调增区间为______. (6)函数()()2f x sin x ϕ=+,其中ϕ为实数,若()6f x f π⎛⎫≤⎪⎝⎭对x R ∈ 恒成立,且()f x 的单调递增区间是______.答案:(1)2,,63k k k z ππππ⎡⎤++∈⎢⎥⎣⎦;27,,36k k k z ππππ⎡⎤++∈⎢⎥⎣⎦ (2)2(3)Z k k k ∈++-],6,3[ππππ解析:由题意得,π=T 则1,()sin(2).6f x x πω=∴=+由222,262k x k πππππ-+≤+≤+解得.,63Z k k x k ∈+≤≤+-ππππ故)(x f 的单调增区间是Z k k k ∈++-],6,3[ππππ.(4)()22,12343k k k z ππππ⎡⎤-++∈⎢⎥⎣⎦ (5)(),2k k k z πππ⎛⎫+∈ ⎪⎝⎭(6)()263k ,k k Z ππππ⎡⎤++∈⎢⎥⎣⎦题型三:由sin()y A x ωϕ=+的图象求其函数式 (1)已知函数sin()y A x ωϕ=+),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的图象如图所示,则该函数的解析式是________.(2)函数sin()(0,0,||)2y A x A πωϕωϕ=+>><的图象如图所示,则y的表达式为________.(3)如图所示,是函数sin()y A x k ωϕ=++(0A >,0ω>,||2πϕ<)的图象的一部分,则函数解析式是________.答案:(1))48sin(4π+π-=x y (2))62sin(2π+=x y 解析:由图像可知最大值为2,所以A=2,周期22236T πππω⎛⎫=-=∴= ⎪⎝⎭,代入点,26π⎛⎫ ⎪⎝⎭得sin 136ππϕϕ⎛⎫+=∴= ⎪⎝⎭,所以函数式为)62sin(2π+=x y(3)2sin(2)16y x π=++题型四:求三角函数的周期(1)设函数)sin()(ϕω+=x x f ,0,0>>ωA ,若)(x f 在区间]2,6[ππ上单调,且⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛6322πππf f f ,则)(x f 的最小正周期为________. (2)函数cos(2)sin(2)36y x x ππ=---的最小正周期__________.(3)函数f (x )=sin x +cos x )cos x –sin x )的最小正周期是________. (4)函数()2sin sin cos 1f x x x x =++的最小正周期是 . (5)函数x x f 2sin 31)(-=的最小正周期为 .(6)已知函数()2sin 2xf x x =-.则()f x 的最小正周期为 . (7)函数()sin 3cos5f x x x =+的最小正周期为 .答案:(1)π解析:)sin()(ϕω+=x x f 在区间]2,6[ππ上单调,0>ω,ωπωπππ=⋅=≤∴22126-2T ,即30≤<ω,又⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛6322πππf f f ,1272322πππ=+=∴x 为)sin()(ϕω+=x x f 的一条对称轴,且3262πππ=+,则)0,3(π为)sin()(ϕω+=x x f 的一个对称中心,由于30≤<ω,所以127π=x 与)0,3(π为同一周期里相邻的对称轴和对称中心,则πππ=-=)3127(4T (2)π(3)π (4)π (5)π (6)2π(7)2π 解析:因为sin 3x 的最小正周期123T π=,cos5x 最小正周期225T π=,所以函数()sin 3cos5f x x x =+的最小正周期为2π题型五:三角函数的最值(1)函数x x x f sin 22cos )(+=的最小值为 .(2)函数2474sin cos 4cos 4cos y x x x x =-+-的最大值为 ;最小值为 .(3)已知函数()22sin cos 44f x x x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,则()f x 在02x π⎡⎤∈⎢⎥⎣⎦,上的最大值与最小值之差为 .(4)设当x θ=时,函数()2sin cos f x x x =-取得最大值,则cos θ=__________.(5)已知函数()sin cos f x x a x =+图象的一条对称轴是4x π=,且当x θ=时,函数()sin ()g x x f x =+取得最大值,则cos θ= .(6)已知1)4(cos 2)sin (cos 3)(222++--=πx x x x f 的定义域为[2,0π].则)(x f 的最小值为 .(7)函数sin 52sin x y x +=-的最大值为 .(8)函数2sin 2cos xy x-=-的最小值为 .(9)函数21sin 1sin xy x--=-在区间[0,)2π上的最小值为 .答案:(1)3-(2)10;6 解析:2474sin cos 4cos 4cos y x x x x =-+-()2272sin 24cos 1cos x x x =-+-2272sin 24cos sin x x x =-+272sin 2sin 2x x =-+()21sin 26x =-+令sin 2,[1,1]x μμ=∈-,由于函数()216z u =-+在[]11-,中的最大值为()2max 11610z =--+=最小值为()2min 1166z =-+=故当sin 21x =-时y 取得最大值10,当sin 21x =时y 取得最小值6. (3)3(4)()()2sin cos f x x x x φ=-=-,其中cos φφ==故当函数()f x 取得最大值时,2,,cos cos 2sin 22k k Z k ππθφπθφπφ⎛⎫-=+∈∴=++=-= ⎪⎝⎭(5(6)(7)6(8解析:设(2,2),(cosx,sinx),A P 则2sin 2cos PA x k x -=-,即PA k 为过点,A P 两点的斜率. 所以要求函数2sin 2cos xy x-=-的最大值,只要求直线PA 的斜率PA k 的最大值即可.因为22cos x sin x 1+=,所以(cosx,sinx)P 在单位圆上.因为直线PA 的方程为:(2)2PA y k x =--,所以直线PA 与单位圆相切时,斜率PA k 取得最值.1,解得PA k =2sin 2cos x y x -=-(9题型六:三角函数的对称性(1)若把函数cos y x x =的图像向左平移m 个单位()0m >后,所得到的图像关于y 轴对称,则m 的最小值为 .(2)已知函数y =A sin(2x +φ)的对称轴为x =π6,则φ的值为 .(3)若函数f (x )=sin(x +θ)(0<θ<π2)的图象关于直线x =π6对称,则θ= .(4)将函数f (x )=2sin(2x -π6)的图象向左平移m 个单位(m >0),若所得的图象关于直线x =π6对称,则m 的最小值为 . (5)已知函数f (x )=3sin(ωx -π6)(ω>0)和g (x )=3cos(2x +φ)的图象的对称中心完全相同,若x ∈[0,π2],则f (x )的取值范围是________. 答案:(1)23π(2)k π+π6(k ∈Z )(3)π3(4)π6(5)[-32,3]解析:由3sin(ωx -π6)=0,得ωx =k π+π6(k ∈Z),∴x =k πω+π6ω,即对称中心为(k πω+π6ω,0)(k ∈Z).由3cos(2x +φ)=0得2x =k π+π2-φ(k ∈Z),∴x =k π2+π4-φ2,即对称中心为(k π2+π4-φ2,0)(k ∈Z).∴k πω=k π2得ω=2,故f (x )=3sin(2x -π6),∵x ∈[0,π2],∴-12≤sin(2x -π6)≤1, 故-32≤f (x )≤3.。


♦♦♦学生用书(后跟详细参考答案和教师用书)♦♦♦把握命题趋势,提高复习效率,提升解题能力,打造高考高分!【助力高考】2019年高考备战数学专题复习精品资料第四章 三角函数、解三角形第20讲 三角函数的图象和性质★★★核心知识回顾★★★知识点一、用五点法作正弦函数和余弦函数的简图(1)在正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0).(2)在余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝⎛⎭⎫π2,0, ,⎝⎛⎭⎫3π2,0,(2π,1).知识点二、正弦、余弦、正切函数的图象与性质(下表中k ∈Z)π★★★高考典例剖析★★★________.答案⎣⎡⎦⎤2kπ+π4,2kπ+5π4(k∈Z)解析方法一要使函数有意义,必须使sin x-cos x≥0.利用图象,在同一坐标系中画出[0,2π]上y=sin x和y=cos x的图象,如图所示.在[0,2π]内,满足sin x=cos x的x为π4,5π4,再结合正弦、余弦函数的周期是2π,所以原函数的定义域为⎩⎨⎧⎭⎬⎫x⎪⎪2kπ+π4≤x≤2kπ+5π4,k∈Z.方法二利用三角函数线,画出满足条件的终边范围(如图阴影部分所示).所以定义域为⎩⎨⎧⎭⎬⎫x⎪⎪2kπ+π4≤x≤2kπ+5π4,k∈Z.1.函数f (x )=-2tan ⎝⎛⎭⎫2x +π6的定义域是( ) A.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠π6 B.⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠-π12 C.⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π+π6(k ∈Z ) D.⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2+π6(k ∈Z ) 2.已知函数f (x )=sin ⎝⎛⎭⎫x +π6,其中x ∈⎣⎡⎦⎤-π3,a ,若f (x )的值域是⎣⎡⎦⎤-12,1,则实数a 的取值范围是________.3.(2018·长沙质检)函数y =sin x -cos x +sin x cos x 的值域为__________. 考点二、三角函数的单调性 命题点1 求三角函数的单调性例2:函数f (x )=tan ⎝⎛⎭⎫2x -π3的单调递增区间是( ) A.⎣⎡⎦⎤k π2-π12,k π2+5π12(k ∈Z ) B.⎝⎛⎭⎫k π2-π12,k π2+5π12(k ∈Z ) C.⎝⎛⎭⎫k π+π6,k π+2π3(k ∈Z ) D.⎣⎡⎦⎤k π-π12,k π+5π12(k ∈Z ) 答案 B解析 由k π-π2<2x -π3<k π+π2(k ∈Z ),得k π2-π12<x <k π2+5π12(k ∈Z ), 所以函数f (x )=tan ⎝⎛⎭⎫2x -π3的单调递增区间为⎝⎛⎭⎫k π2-π12,k π2+5π12(k ∈Z ),故选B. 命题点2 根据单调性求参数例3: 已知ω>0,函数f (x )=sin ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递减,则ω的取值范围是________. 答案 ⎣⎡⎦⎤12,54解析 由π2<x <π,ω>0,得ωπ2+π4<ωx +π4<ωπ+π4, 又y =sin x 的单调递减区间为⎣⎡⎦⎤2k π+π2,2k π+3π2,k ∈Z , 所以⎩⎨⎧ωπ2+π4≥π2+2k π,ωπ+π4≤3π2+2k πk ∈Z ,解得4k +12≤ω≤2k +54,k ∈Z .又由4k +12-⎝⎛⎭⎫2k +54≤0,k ∈Z 且2k +54>0,k ∈Z ,得k =0,所以ω∈⎣⎡⎦⎤12,54.4. (2017·哈尔滨、长春、沈阳、大连四市联考)函数y =12sin x +32cos x ⎝⎛⎭⎫x ∈⎣⎡⎦⎤0,π2的单调递增区间是____________.5.若已知ω>0,函数f (x )=cos ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递增,则ω的取值范围是____. 6. (2017·济南模拟)若函数f (x )=sin ωx (ω>0)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω等于( )A.23B.32 C .2D .3考点三、三角函数的周期性、奇偶性、对称性 命题点1 三角函数的周期性例4:在函数①y =cos|2x |,②y =|cos x |,③y =cos ⎝⎛⎭⎫2x +π6,④y =tan ⎝⎛⎭⎫2x -π4中,最小正周期为π的所有函数为( ) A .①②③ B .①③④ C .②④ D .①③答案 A解析 ①y =cos|2x |=cos 2x ,最小正周期为π; ②由图象知y =|cos x |的最小正周期为π; ③y =cos ⎝⎛⎭⎫2x +π6的最小正周期T =2π2=π; ④y =tan ⎝⎛⎭⎫2x -π4的最小正周期T =π2,故选A. 命题点2 三角函数的奇偶性例5: (2017·银川模拟)函数f (x )=3sin ⎝⎛⎭⎫2x -π3+φ,φ∈(0,π)满足f (|x |)=f (x ),则φ的值为______. 答案5π6解析 由题意知f (x )为偶函数,关于y 轴对称, ∴f (0)=3sin ⎝⎛⎭⎫φ-π3=±3,∴φ-π3=k π+π2,k ∈Z ,又0<φ<π,∴φ=5π6.命题点3 三角函数图象的对称性例6: (2018·武汉模拟)若函数y =cos ⎝⎛⎭⎫ωx +π6(ω∈N *)图象的一个对称中心是⎝⎛⎭⎫π6,0,则ω的最小值为________. 答案 2解析 由题意知ω6π+π6=k π+π2(k ∈Z ),∴ω=6k +2(k ∈Z ),又ω∈N *,∴ωmin =2.6.若函数f (x )=2tan ⎝⎛⎭⎫kx +π3的最小正周期T 满足1<T <2,则自然数k 的值为________. 7.已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|≤π2,x =-π4为f (x )的零点,x =π4为y =f (x )图象的对称轴,且f (x )在⎝⎛⎫π18,5π36上单调,则ω的最大值为________.8.(2017·安徽江南十校联考)已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2的最小正周期为4π,且∀x ∈R ,有f (x )≤f ⎝⎛⎭⎫π3成立,则f (x )图象的一个对称中心坐标是( ) A.⎝⎛⎭⎫-2π3,0 B.⎝⎛⎭⎫-π3,0 C.⎝⎛⎭⎫2π3,0D.⎝⎛⎭⎫5π3,09.若将函数f (x )=sin ⎝⎛⎭⎫ωx +π3的图象向右平移π3个单位长度后与原函数的图象关于x 轴对称,则ω的最小正值是________.10.(2017·全国Ⅲ)设函数f (x )=cos ⎝⎛⎭⎫x +π3,则下列结论错误的是( ) A .f (x )的一个周期为-2πB .y =f (x )的图象关于直线x =8π3对称C .f (x +π)的一个零点为x =π6D .f (x )在⎝⎛⎭⎫π2,π上单调递减11.函数f (x )=cos(ωx +φ)的部分图象如图所示,则f (x )的单调递减区间为________.12.设函数f (x )=A sin(ωx +φ)(A ,ω,φ是常数,A >0,ω>0).若f (x )在区间⎣⎡⎦⎤π6,π2上具有单调性,且f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3=-f ⎝⎛⎭⎫π6,则f (x )的最小正周期为________.★★★知能达标演练★★★一、选择题1.下列函数中最小正周期为π且图象关于直线x =π3对称的是( )A .y =2sin ⎝⎛⎭⎫2x +π3B .y =2sin ⎝⎛⎭⎫2x -π6 C .y =2sin ⎝⎛⎭⎫x 2+π3D .y =2sin ⎝⎛⎭⎫2x -π3 2.(2018·广州质检)下列函数中,是周期函数的为( ) A .y =sin|x | B .y =cos|x | C .y =tan|x |D .y =(x -1)03.函数f (x )=sin ⎝⎛⎭⎫2x -π4在区间⎣⎡⎦⎤0,π2上的最小值为( ) A .-1 B .-22 C.22D .0 4.函数y =sin x 2的图象是( )5.(2017·成都诊断)函数y =cos 2x -2sin x 的最大值与最小值分别为( ) A .3,-1 B .3,-2 C .2,-1 D .2,-26.已知函数f (x )=2sin(2x +φ)⎝⎛⎭⎫|φ|<π2的图象过点(0,3),则f (x )图象的一个对称中心是( ) A.⎝⎛⎭⎫-π3,0 B.⎝⎛⎭⎫-π6,0 C.⎝⎛⎭⎫π6,0D.⎝⎛⎭⎫π12,07.(2017·衡水模拟)已知函数f (x )=⎪⎪⎪⎪tan ⎝⎛⎭⎫12x -π6,则下列说法正确的是( ) A .f (x )的周期是π2B .f (x )的值域是{y |y ∈R ,且y ≠0}C .直线x =5π3是函数f (x )图象的一条对称轴D .f (x )的单调递减区间是⎝⎛⎦⎤2k π-2π3,2k π+π3,k ∈Z 8.(2018·太原模拟)若f (x )=3sin x -4cos x 的一条对称轴方程是x =a ,则a 的取值范围可以是( ) A.⎝⎛⎭⎫0,π4 B.⎝⎛⎭⎫π4,π2 C.⎝⎛⎭⎫π2,3π4D.⎝⎛⎭⎫3π4,π9.已知函数f (x )=2cos(ωx +φ)+b 对任意实数x 有f ⎝⎛⎭⎫x +π4=f (-x )恒成立,且f ⎝⎛⎭⎫π8=1,则实数b 的值为( ) A .-1 B .3 C .-1或3 D .-3二、填空题10.函数f (x )=cos ⎝⎛⎭⎫2x +π4的最小正周期是________. 11. y =3sin ⎝⎛⎭⎫2x -π6在区间⎣⎡⎦⎤0,π2上的值域是________.12. y =tan 2x 的定义域是________.13.函数f (x )=4sin ⎝⎛⎭⎫π3-2x 的单调递减区间是______________________. 14.cos 23°,sin 68°,cos 97°的大小关系是________. 15.函数y =cos ⎝⎛⎭⎫π4-2x 的单调递减区间为__________.16.(2018·福州质检)函数y =cos 2x +sin x ⎝⎛⎭⎫|x |≤π4的最小值为____________. 17.已知函数f (x )=2sin ⎝⎛⎭⎫ωx -π6+1(x ∈R )的图象的一条对称轴为x =π,其中ω为常数,且ω∈(1,2),则函数f (x )的最小正周期为________.18.(2018·珠海模拟)设函数f (x )=3sin ⎝⎛⎭⎫π2x +π4,若存在这样的实数x 1,x 2,对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为________.19.已知关于x 的方程2sin ⎝⎛⎭⎫x +π6+1-a =0在区间⎣⎡⎦⎤0,2π3上存在两个根,则实数a 的取值范围是________. 三、解答题20.已知f (x )=2sin ⎝⎛⎭⎫2x +π4. (1)求函数f (x )图象的对称轴方程; (2)求f (x )的单调递增区间;(3)当x ∈⎣⎡⎦⎤π4,3π4时,求函数f (x )的最大值和最小值. 21. (2017·武汉调研)已知函数f (x )=a ⎝⎛⎭⎫2cos 2x2+sin x +b . (1)若a =-1,求函数f (x )的单调增区间;(2)当x ∈[0,π]时,函数f (x )的值域是[5,8],求a ,b 的值.22.(2018·兰州模拟)已知a >0,函数f (x )=-2a sin ⎝⎛⎭⎫2x +π6+2a +b ,当x ∈⎣⎡⎦⎤0,π2时, -5≤f (x )≤1.(1)求常数a ,b 的值;(2)设g (x )=f ⎝⎛⎭⎫x +π2且lg g (x )>0,求g (x )的单调区间.♦♦♦学生用书(后跟详细参考答案和教师用书)♦♦♦把握命题趋势,提高复习效率,提升解题能力,打造高考高分!【助力高考】2019年高考备战数学专题复习精品资料第四章 三角函数、解三角形第20讲 三角函数的图象和性质★★★核心知识回顾★★★知识点一、用五点法作正弦函数和余弦函数的简图(1)在正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0).(2)在余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫3π2,0,(2π,1).知识点二、正弦、余弦、正切函数的图象与性质(下表中k ∈Z)π★★★高考典例剖析★★★考点一、三角函数的定义域和值域♦♦♦跟踪训练♦♦♦1.答案 D解析 由正切函数的定义域,得2x +π6≠k π+π2,k ∈Z ,即x ≠k π2+π6(k ∈Z ),故选D. 2.答案 ⎣⎡⎦⎤π3,π解析 ∵x ∈⎣⎡⎦⎤-π3,a ,∴x +π6∈⎣⎡⎦⎤-π6,a +π6, ∵当x +π6∈⎣⎡⎦⎤-π6,π2时,f (x )的值域为⎣⎡⎦⎤-12,1, ∴由函数的图象(图略)知π2≤a +π6≤7π6,∴π3≤a ≤π. 3.答案 ⎣⎡⎦⎤-12-2,1 解析 设t =sin x -cos x ,则t 2=sin 2x +cos 2x -2sin x ·cos x ,sin x cos x =1-t 22,且-2≤t ≤ 2. ∴y =-t 22+t +12=-12(t -1)2+1,t ∈[-2,2]. 当t =1时,y max =1;当t =-2时,y min =-12- 2. ∴函数的值域为⎣⎡⎦⎤-12-2,1.考点二、三角函数的单调性♦♦♦跟踪训练♦♦♦4.答案 ⎣⎡⎦⎤0,π6 解析 ∵y =12sin x +32cos x =sin ⎝⎛⎭⎫x +π3, 由2k π-π2≤x +π3≤2k π+π2(k ∈Z ), 解得2k π-5π6≤x ≤2k π+π6(k ∈Z ). ∴函数的单调递增区间为⎣⎡⎦⎤2k π-5π6,2k π+π6(k ∈Z ), 又x ∈⎣⎡⎦⎤0,π2,∴单调递增区间为⎣⎡⎦⎤0,π6. 5.答案 ⎣⎡⎦⎤32,74解析 函数y =cos x 的单调递增区间为[-π+2k π,2k π],k ∈Z ,则⎩⎨⎧ ωπ2+π4≥-π+2k π,ωπ+π4≤2k πk ∈Z ,解得4k -52≤ω≤2k -14,k ∈Z , 又由4k -52-⎝⎛⎭⎫2k -14≤0,k ∈Z 且2k -14>0,k ∈Z , 得k =1,所以ω∈⎣⎡⎦⎤32,74.6. 答案 B解析 由已知得T 4=π3, ∴T =4π3,∴ω=2πT =32. 考点三、三角函数的周期性、奇偶性、对称性♦♦♦跟踪训练♦♦♦6.答案 2或3解析 由题意得,1<πk<2, ∴k <π<2k ,即π2<k <π, 又k ∈Z ,∴k =2或3.7.答案 9解析 因为x =-π4为f (x )的零点,x =π4为f (x )的图象的对称轴,所以π4-⎝⎛⎭⎫-π4=T 4+kT 2,即π2=2k +14T =2k +14·2πω,所以ω=2k +1(k ∈N ),又因为f (x )在⎝⎛⎭⎫π18,5π36上单调,所以5π36-π18=π12≤T 2=2π2ω,即ω≤12, 若ω=11,又|φ|≤π2,则φ=-π4, 此时,f (x )=sin ⎝⎛⎭⎫11x -π4,f (x )在⎝⎛⎭⎫π18,3π44上单调递增,在⎝⎛⎭⎫3π44,5π36上单调递减,不满足条件. 若ω=9,又|φ|≤π2,则φ=π4, 此时,f (x )=sin ⎝⎛⎭⎫9x +π4,满足f (x )在⎝⎛⎭⎫π18,5π36上单调的条件. 由此得ω的最大值为9.8.答案 A解析 由f (x )=sin(ωx +φ)的最小正周期为4π,得ω=12. 因为f (x )≤f ⎝⎛⎭⎫π3恒成立,所以f (x )max =f ⎝⎛⎭⎫π3,即12×π3+φ=π2+2k π(k ∈Z ), 由|φ|<π2,得φ=π3,故f (x )=sin ⎝⎛⎭⎫12x +π3. 令12x +π3=k π(k ∈Z ),得x =2k π-2π3(k ∈Z ), 故f (x )图象的对称中心为⎝⎛⎭⎫2k π-2π3,0(k ∈Z ), 当k =0时,f (x )图象的对称中心为⎝⎛⎭⎫-2π3,0. 9.答案 3解析 若将函数f (x )的图象向右平移π3个单位长度后与原函数的图象关于x 轴对称,则平移的大小最小为T 2,所以T 2≤π3,即T max =2π3,所以当T =2π3时,ωmin =2πT max =2π2π3=3. 10.答案 D解析 A 项,因为f (x )=cos ⎝⎛⎭⎫x +π3的周期为2k π(k ∈Z ),所以f (x )的一个周期为-2π,A 项正确;B 项,因为f (x )=cos ⎝⎛⎭⎫x +π3图象的对称轴为直线x =k π-π3(k ∈Z ),所以y =f (x )的图象关于直线x =8π3对称,B 项正确; C 项,f (x +π)=cos ⎝⎛⎭⎫x +4π3.令x +4π3=k π+π2(k ∈Z ),得x =k π-5π6,当k =1时,x =π6,所以f (x +π)的一个零点为x =π6,C 项正确; D 项,因为f (x )=cos ⎝⎛⎭⎫x +π3的单调递减区间为⎣⎡⎦⎤2k π-π3,2k π+2π3(k ∈Z ), 单调递增区间为⎣⎡⎦⎤2k π+2π3,2k π+5π3(k ∈Z ), 所以⎝⎛⎭⎫π2,2π3是f (x )的单调递减区间,⎣⎡⎭⎫2π3,π是f (x )的单调递增区间,D 项错误.故选D. 11.答案 ⎝⎛⎭⎫2k -14,2k +34,k ∈Z 解析 由图象知,周期T =2×⎝⎛⎭⎫54-14=2,∴2πω=2,∴ω=π. 由π×14+φ=π2+2k π,k ∈Z ,不妨取φ=π4, ∴f (x )=cos ⎝⎛⎭⎫πx +π4. 由2k π<πx +π4<2k π+π,k ∈Z ,得2k -14<x <2k +34,k ∈Z ,∴f (x )的单调递减区间为⎝⎛⎭⎫2k -14,2k +34,k ∈Z . 12.答案 π解析 记f (x )的最小正周期为T .由题意知T 2≥π2-π6=π3, 又f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3=-f ⎝⎛⎭⎫π6, 且2π3-π2=π6, 可作出示意图如图所示(一种情况):∴x 1=⎝⎛⎭⎫π2+π6×12=π3,x 2=⎝⎛⎭⎫π2+2π3×12=7π12,∴T 4=x 2-x 1=7π12-π3=π4,∴T =π. ★★★知能达标演练★★★一、选择题1.答案 B解析 函数y =2sin ⎝⎛⎭⎫2x -π6的周期T =2π2=π, 又sin ⎝⎛⎭⎫2×π3-π6=1, ∴函数y =2sin ⎝⎛⎭⎫2x -π6的图象关于直线x =π3对称. 2.答案 B解析 ∵cos|x |=cos x ,∴y =cos|x |是周期函数.3.答案 B解析 由已知x ∈⎣⎡⎦⎤0,π2,得2x -π4∈⎣⎡⎦⎤-π4,3π4, 所以sin ⎝⎛⎭⎫2x -π4∈⎣⎡⎦⎤-22,1, 故函数f (x )=sin ⎝⎛⎭⎫2x -π4在区间⎣⎡⎦⎤0,π2上的最小值为-22.故选B. 4.答案 D解析 函数y =sin x 2为偶函数,排除A ,C ;又当x =π2时函数取得最大值,排除B ,故选D.5.答案 D解析 y =cos 2x -2sin x =1-sin 2x -2sin x=-sin 2x -2sin x +1,令t =sin x ,则t ∈[-1,1],y =-t 2-2t +1=-(t +1)2+2,所以y max =2,y min =-2.6.答案 B解析 函数f (x )=2sin(2x +φ)⎝⎛⎭⎫|φ|<π2的图象过点(0,3),则f (0)=2sin φ=3,∴sin φ=32, 又|φ|<π2,∴φ=π3, 则f (x )=2sin ⎝⎛⎭⎫2x +π3,令2x +π3=k π(k ∈Z ), 则x =k π2-π6(k ∈Z ),当k =0时,x =-π6, ∴⎝⎛⎭⎫-π6,0是函数f (x )的图象的一个对称中心. 7.答案 D解析 函数f (x )的周期为2π,A 错;f (x )的值域为[0,+∞),B 错;当x =5π3时,12x -π6=2π3≠k π2,k ∈Z ,∴x =5π3不是f (x )的对称轴,C 错;令k π-π2<12x -π6≤k π,k ∈Z ,可得2k π-2π3<x ≤2k π+π3,k ∈Z ,∴f (x )的单调递减区间是⎝⎛⎦⎤2k π-2π3,2k π+π3,k ∈Z ,D 正确. 8.答案 D解析 因为f (x )=3sin x -4cos x =5sin(x -φ)⎝⎛⎭⎫其中tan φ=43且0<φ<π2,则sin(a -φ)=±1, 所以a -φ=k π+π2,k ∈Z ,即a =k π+π2+φ,k ∈Z ,而tan φ=43且0<φ<π2,所以π4<φ<π2,所以k π+3π4<a <k π+π,k ∈Z ,取k =0,此时a ∈⎝⎛⎭⎫3π4,π,故选D. 9.答案 C解析 由f ⎝⎛⎭⎫x +π4=f (-x )可知函数f (x )=2cos(ωx +φ)+b 关于直线x =π8对称,又函数f (x )在对称轴处取得最值,故±2+b =1,∴b =-1或b =3.二、填空题10.答案 π11.答案 ⎣⎡⎦⎤-32,3 解析 当x ∈⎣⎡⎦⎤0,π2时,2x -π6∈⎣⎡⎦⎤-π6,5π6, sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤-12,1, 故3sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤-32,3, 即y =3sin ⎝⎛⎭⎫2x -π6的值域为⎣⎡⎦⎤-32,3.12.答案 ⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2+π4,k ∈Z 解析 由2x ≠k π+π2,k ∈Z ,得x ≠k π2+π4,k ∈Z , ∴y =tan 2x 的定义域是⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2+π4,k ∈Z . 13.答案 ⎣⎡⎦⎤k π-π12,k π+512π(k ∈Z ) 解析 f (x )=4sin ⎝⎛⎭⎫π3-2x =-4sin ⎝⎛⎭⎫2x -π3. 所以要求f (x )的单调递减区间,只需求y =4sin ⎝⎛⎭⎫2x -π3的单调递增区间. 由-π2+2k π≤2x -π3≤π2+2k π(k ∈Z ),得 -π12+k π≤x ≤512π+k π(k ∈Z ). 所以函数f (x )的单调递减区间是⎣⎡⎦⎤-π12+k π,512π+k π(k ∈Z ). 14.答案 sin 68°>cos 23°>cos 97°解析 sin 68°=cos 22°,又y =cos x 在[0°,180°]上是减函数,∴sin 68°>cos 23°>cos 97°.15.答案 ⎣⎡⎦⎤k π+π8,k π+5π8(k ∈Z ) 解析 因为y =cos ⎝⎛⎭⎫π4-2x =cos ⎝⎛⎭⎫2x -π4, 所以令2k π≤2x -π4≤2k π+π(k ∈Z ), 解得k π+π8≤x ≤k π+5π8(k ∈Z ), 所以函数的单调递减区间为⎣⎡⎦⎤k π+π8,k π+5π8(k ∈Z ). 16.答案 1-22解析 令t =sin x ,∵|x |≤π4,∴t ∈⎣⎡⎦⎤-22,22. ∴y =-t 2+t +1=-⎝⎛⎭⎫t -122+54, ∴当t =-22时,y min =1-22.17.答案 6π5解析 由函数f (x )=2sin ⎝⎛⎭⎫ωx -π6+1(x ∈R )的图象的一条对称轴为x =π,可得ωπ-π6=k π+π2,k ∈Z ,∴ω=k +23,又ω∈(1,2),∴ω=53, 从而得函数f (x )的最小正周期为2π53=6π5. 18.答案 2解析 |x 1-x 2|的最小值为函数f (x )的半个周期,又T =4,∴|x 1-x 2|的最小值为2.19.答案 [2,3)解析 sin ⎝⎛⎭⎫x +π6=a -12在⎣⎡⎦⎤0,2π3上存在两个根,设x +π6=t ,则t ∈⎣⎡⎦⎤π6,5π6, ∴y =sin t ,t ∈⎣⎡⎦⎤π6,5π6的图象与直线y =a -12有两个交点,∴12≤a -12<1,∴2≤a <3. 三、解答题20.解 (1)f (x )=2sin ⎝⎛⎭⎫2x +π4, 令2x +π4=k π+π2,k ∈Z , 得x =k π2+π8,k ∈Z . 所以函数f (x )图象的对称轴方程是x =k π2+π8,k ∈Z . (2)令2k π-π2≤2x +π4≤2k π+π2,k ∈Z , 得k π-3π8≤x ≤k π+π8,k ∈Z . 故f (x )的单调递增区间为⎣⎡⎦⎤k π-3π8,k π+π8,k ∈Z . (3)当x ∈⎣⎡⎦⎤π4,3π4时,3π4≤2x +π4≤7π4, 所以-1≤sin ⎝⎛⎭⎫2x +π4≤22, 所以-2≤f (x )≤1,所以当x ∈⎣⎡⎦⎤π4,3π4时,函数f (x )的最大值为1,最小值为- 2.21.解 f (x )=a (1+cos x +sin x )+b=2a sin ⎝⎛⎭⎫x +π4+a +b . (1)当a =-1时,f (x )=-2sin ⎝⎛⎭⎫x +π4+b -1, 由2k π+π2≤x +π4≤2k π+3π2(k ∈Z ), 得2k π+π4≤x ≤2k π+5π4(k ∈Z ), ∴f (x )的单调增区间为⎣⎡⎦⎤2k π+π4,2k π+5π4(k ∈Z ). (2)∵0≤x ≤π,∴π4≤x +π4≤5π4, ∴-22≤sin ⎝⎛⎭⎫x +π4≤1.依题意知a ≠0, ①当a >0时,⎩⎨⎧ 2a +a +b =8,b =5,∴a =32-3,b =5; ②当a <0时,⎩⎨⎧b =8,2a +a +b =5,∴a =3-32,b =8. 综上所述,a =32-3,b =5或a =3-32,b =8.22.解 (1)∵x ∈⎣⎡⎦⎤0,π2,∴2x +π6∈⎣⎡⎦⎤π6,7π6, ∴sin ⎝⎛⎭⎫2x +π6∈⎣⎡⎦⎤-12,1, ∴-2a sin ⎝⎛⎭⎫2x +π6∈[-2a ,a ], ∴f (x )∈[b,3a +b ],又∵-5≤f (x )≤1,∴b =-5,3a +b =1,因此a =2,b =-5.(2)由(1)得f (x )=-4sin ⎝⎛⎭⎫2x +π6-1, g (x )=f ⎝⎛⎭⎫x +π2=-4sin ⎝⎛⎭⎫2x +7π6-1 =4sin ⎝⎛⎭⎫2x +π6-1, 又由lg g (x )>0,得g (x )>1,∴4sin ⎝⎛⎭⎫2x +π6-1>1,∴sin ⎝⎛⎭⎫2x +π6>12, ∴2k π+π6<2x +π6<2k π+5π6,k ∈Z , 其中当2k π+π6<2x +π6≤2k π+π2,k ∈Z 时,g (x )单调递增,即k π<x ≤k π+π6,k ∈Z , ∴g (x )的单调增区间为⎝⎛⎦⎤k π,k π+π6,k ∈Z . 又∵当2k π+π2<2x +π6<2k π+5π6,k ∈Z 时, g (x )单调递减,即k π+π6<x <k π+π3,k ∈Z . ∴g (x )的单调减区间为⎝⎛⎭⎫k π+π6,k π+π3,k ∈Z . ∴g (x )的单调增区间为⎝⎛⎦⎤k π,k π+π6,k ∈Z , 单调减区间为⎝⎛⎭⎫k π+π6,k π+π3,k ∈Z .♦♦♦教师用书♦♦♦把握命题趋势,提高复习效率,提升解题能力,打造高考高分!【助力高考】2019年高考备战数学专题复习精品资料第四章 三角函数、解三角形第20讲 三角函数的图象和性质★★★核心知识回顾★★★知识点一、用五点法作正弦函数和余弦函数的简图(1)在正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0).(2)在余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫3π2,0,(2π,1).知识点二、正弦、余弦、正切函数的图象与性质(下表中k ∈Z)π★★★高考典例剖析★★★________.答案⎣⎡⎦⎤2kπ+π4,2kπ+5π4(k∈Z)解析方法一要使函数有意义,必须使sin x-cos x≥0.利用图象,在同一坐标系中画出[0,2π]上y=sin x和y=cos x的图象,如图所示.在[0,2π]内,满足sin x=cos x的x为π4,5π4,再结合正弦、余弦函数的周期是2π,所以原函数的定义域为⎩⎨⎧⎭⎬⎫x⎪⎪2kπ+π4≤x≤2kπ+5π4,k∈Z.方法二利用三角函数线,画出满足条件的终边范围(如图阴影部分所示).所以定义域为⎩⎨⎧⎭⎬⎫x⎪⎪2kπ+π4≤x≤2kπ+5π4,k∈Z.1.函数f (x )=-2tan ⎝⎛⎭⎫2x +π6的定义域是( ) A.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠π6 B.⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠-π12 C.⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π+π6(k ∈Z ) D.⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2+π6(k ∈Z ) 答案 D解析 由正切函数的定义域,得2x +π6≠k π+π2,k ∈Z ,即x ≠k π2+π6(k ∈Z ),故选D.2.已知函数f (x )=sin ⎝⎛⎭⎫x +π6,其中x ∈⎣⎡⎦⎤-π3,a ,若f (x )的值域是⎣⎡⎦⎤-12,1,则实数a 的取值范围是________. 答案 ⎣⎡⎦⎤π3,π解析 ∵x ∈⎣⎡⎦⎤-π3,a ,∴x +π6∈⎣⎡⎦⎤-π6,a +π6, ∵当x +π6∈⎣⎡⎦⎤-π6,π2时,f (x )的值域为⎣⎡⎦⎤-12,1, ∴由函数的图象(图略)知π2≤a +π6≤7π6,∴π3≤a ≤π.3.(2018·长沙质检)函数y =sin x -cos x +sin x cos x 的值域为__________. 答案 ⎣⎡⎦⎤-12-2,1 解析 设t =sin x -cos x ,则t 2=sin 2x +cos 2x -2sin x ·cos x ,sin x cos x =1-t 22,且-2≤t ≤ 2.∴y =-t 22+t +12=-12(t -1)2+1,t ∈[-2,2].当t =1时,y max =1;当t =-2时,y min =-12- 2.∴函数的值域为⎣⎡⎦⎤-12-2,1. 考点二、三角函数的单调性 命题点1 求三角函数的单调性例2:函数f (x )=tan ⎝⎛⎭⎫2x -π3的单调递增区间是( ) A.⎣⎡⎦⎤k π2-π12,k π2+5π12(k ∈Z ) B.⎝⎛⎭⎫k π2-π12,k π2+5π12(k ∈Z ) C.⎝⎛⎭⎫k π+π6,k π+2π3(k ∈Z ) D.⎣⎡⎦⎤k π-π12,k π+5π12(k ∈Z ) 答案 B解析 由k π-π2<2x -π3<k π+π2(k ∈Z ),得k π2-π12<x <k π2+5π12(k ∈Z ), 所以函数f (x )=tan ⎝⎛⎭⎫2x -π3的单调递增区间为 ⎝⎛⎭⎫k π2-π12,k π2+5π12(k ∈Z ),故选B.命题点2 根据单调性求参数例3: 已知ω>0,函数f (x )=sin ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递减,则ω的取值范围是________. 答案 ⎣⎡⎦⎤12,54解析 由π2<x <π,ω>0,得ωπ2+π4<ωx +π4<ωπ+π4, 又y =sin x 的单调递减区间为⎣⎡⎦⎤2k π+π2,2k π+3π2,k ∈Z , 所以⎩⎨⎧ωπ2+π4≥π2+2k π,ωπ+π4≤3π2+2k πk ∈Z ,解得4k +12≤ω≤2k +54,k ∈Z .又由4k +12-⎝⎛⎭⎫2k +54≤0,k ∈Z 且2k +54>0,k ∈Z ,得k =0,所以ω∈⎣⎡⎦⎤12,54.4. (2017·哈尔滨、长春、沈阳、大连四市联考)函数y =12sin x +32cos x ⎝⎛⎭⎫x ∈⎣⎡⎦⎤0,π2的单调递增区间是____________. 答案 ⎣⎡⎦⎤0,π6 解析 ∵y =12sin x +32cos x =sin ⎝⎛⎭⎫x +π3, 由2k π-π2≤x +π3≤2k π+π2(k ∈Z ),解得2k π-5π6≤x ≤2k π+π6(k ∈Z ).∴函数的单调递增区间为⎣⎡⎦⎤2k π-5π6,2k π+π6(k ∈Z ), 又x ∈⎣⎡⎦⎤0,π2,∴单调递增区间为⎣⎡⎦⎤0,π6. 5.若已知ω>0,函数f (x )=cos ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递增,则ω的取值范围是____. 答案 ⎣⎡⎦⎤32,74解析 函数y =cos x 的单调递增区间为[-π+2k π,2k π],k ∈Z ,则⎩⎨⎧ωπ2+π4≥-π+2k π,ωπ+π4≤2k πk ∈Z ,解得4k -52≤ω≤2k -14,k ∈Z ,又由4k -52-⎝⎛⎭⎫2k -14≤0,k ∈Z 且2k -14>0,k ∈Z ,得k =1,所以ω∈⎣⎡⎦⎤32,74.6. (2017·济南模拟)若函数f (x )=sin ωx (ω>0)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω等于( ) A.23 B.32 C .2 D .3答案 B解析 由已知得T 4=π3,∴T =4π3,∴ω=2πT =32.考点三、三角函数的周期性、奇偶性、对称性 命题点1 三角函数的周期性例4:在函数①y =cos|2x |,②y =|cos x |,③y =cos ⎝⎛⎭⎫2x +π6,④y =tan ⎝⎛⎭⎫2x -π4中,最小正周期为π的所有函数为( ) A .①②③ B .①③④ C .②④ D .①③ 答案 A解析 ①y =cos|2x |=cos 2x ,最小正周期为π; ②由图象知y =|cos x |的最小正周期为π; ③y =cos ⎝⎛⎭⎫2x +π6的最小正周期T =2π2=π; ④y =tan ⎝⎛⎭⎫2x -π4的最小正周期T =π2,故选A. 命题点2 三角函数的奇偶性例5: (2017·银川模拟)函数f (x )=3sin ⎝⎛⎭⎫2x -π3+φ,φ∈(0,π)满足f (|x |)=f (x ),则φ的值为______. 答案5π6解析 由题意知f (x )为偶函数,关于y 轴对称, ∴f (0)=3sin ⎝⎛⎭⎫φ-π3=±3,∴φ-π3=k π+π2,k ∈Z ,又0<φ<π,∴φ=5π6.命题点3 三角函数图象的对称性例6: (2018·武汉模拟)若函数y =cos ⎝⎛⎭⎫ωx +π6(ω∈N *)图象的一个对称中心是⎝⎛⎭⎫π6,0,则ω的最小值为________. 答案 2解析 由题意知ω6π+π6=k π+π2(k ∈Z ),∴ω=6k +2(k ∈Z ),又ω∈N *,∴ωmin =2.6.若函数f (x )=2tan ⎝⎛⎭⎫kx +π3的最小正周期T 满足1<T <2,则自然数k 的值为________. 答案 2或3解析 由题意得,1<πk <2,∴k <π<2k ,即π2<k <π,又k ∈Z ,∴k =2或3.7.已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|≤π2,x =-π4为f (x )的零点,x =π4为y =f (x )图象的对称轴,且f (x )在⎝⎛⎭⎫π18,5π36上单调,则ω的最大值为________. 答案 9解析 因为x =-π4为f (x )的零点,x =π4为f (x )的图象的对称轴,所以π4-⎝⎛⎭⎫-π4=T 4+kT 2,即π2=2k +14T =2k +14·2πω,所以ω=2k +1(k ∈N ),又因为f (x )在⎝⎛⎭⎫π18,5π36上单调,所以5π36-π18=π12≤T2=2π2ω,即ω≤12, 若ω=11,又|φ|≤π2,则φ=-π4,此时,f (x )=sin ⎝⎛⎭⎫11x -π4,f (x )在⎝⎛⎭⎫π18,3π44上单调递增,在⎝⎛⎭⎫3π44,5π36上单调递减,不满足条件. 若ω=9,又|φ|≤π2,则φ=π4,此时,f (x )=sin ⎝⎛⎭⎫9x +π4,满足f (x )在⎝⎛⎭⎫π18,5π36上单调的条件. 由此得ω的最大值为9.8.(2017·安徽江南十校联考)已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2的最小正周期为4π,且∀x ∈R ,有f (x )≤f ⎝⎛⎭⎫π3成立,则f (x )图象的一个对称中心坐标是( ) A.⎝⎛⎭⎫-2π3,0 B.⎝⎛⎭⎫-π3,0 C.⎝⎛⎭⎫2π3,0 D.⎝⎛⎭⎫5π3,0答案 A解析 由f (x )=sin(ωx +φ)的最小正周期为4π, 得ω=12.因为f (x )≤f ⎝⎛⎭⎫π3恒成立, 所以f (x )max =f ⎝⎛⎭⎫π3, 即12×π3+φ=π2+2k π(k ∈Z ), 由|φ|<π2,得φ=π3,故f (x )=sin ⎝⎛⎭⎫12x +π3. 令12x +π3=k π(k ∈Z ),得x =2k π-2π3(k ∈Z ), 故f (x )图象的对称中心为⎝⎛⎭⎫2k π-2π3,0(k ∈Z ), 当k =0时,f (x )图象的对称中心为⎝⎛⎭⎫-2π3,0. 9.若将函数f (x )=sin ⎝⎛⎭⎫ωx +π3的图象向右平移π3个单位长度后与原函数的图象关于x 轴对称,则ω的最小正值是________. 答案 3解析 若将函数f (x )的图象向右平移π3个单位长度后与原函数的图象关于x 轴对称,则平移的大小最小为T 2,所以T 2≤π3,即T max =2π3,所以当T =2π3时,ωmin =2πT max =2π2π3=3.10.(2017·全国Ⅲ)设函数f (x )=cos ⎝⎛⎭⎫x +π3,则下列结论错误的是( ) A .f (x )的一个周期为-2πB .y =f (x )的图象关于直线x =8π3对称C .f (x +π)的一个零点为x =π6D .f (x )在⎝⎛⎭⎫π2,π上单调递减 答案 D解析 A 项,因为f (x )=cos ⎝⎛⎭⎫x +π3的周期为2k π(k ∈Z ),所以f (x )的一个周期为-2π,A 项正确;B 项,因为f (x )=cos ⎝⎛⎭⎫x +π3图象的对称轴为直线x =k π-π3(k ∈Z ),所以y =f (x )的图象关于直线x =8π3对称,B 项正确;C 项,f (x +π)=cos ⎝⎛⎭⎫x +4π3.令x +4π3=k π+π2(k ∈Z ),得x =k π-5π6,当k =1时,x =π6,所以f (x +π)的一个零点为x =π6,C 项正确;D 项,因为f (x )=cos ⎝⎛⎭⎫x +π3的单调递减区间为⎣⎡⎦⎤2k π-π3,2k π+2π3(k ∈Z ), 单调递增区间为⎣⎡⎦⎤2k π+2π3,2k π+5π3(k ∈Z ), 所以⎝⎛⎭⎫π2,2π3是f (x )的单调递减区间,⎣⎡⎭⎫2π3,π是f (x )的单调递增区间,D 项错误.故选D. 11.函数f (x )=cos(ωx +φ)的部分图象如图所示,则f (x )的单调递减区间为________.答案 ⎝⎛⎭⎫2k -14,2k +34,k ∈Z 解析 由图象知,周期T =2×⎝⎛⎭⎫54-14=2, ∴2πω=2,∴ω=π. 由π×14+φ=π2+2k π,k ∈Z ,不妨取φ=π4,∴f (x )=cos ⎝⎛⎭⎫πx +π4.由2k π<πx +π4<2k π+π,k ∈Z ,得2k -14<x <2k +34,k ∈Z ,∴f (x )的单调递减区间为⎝⎛⎭⎫2k -14,2k +34,k ∈Z .12.设函数f (x )=A sin(ωx +φ)(A ,ω,φ是常数,A >0,ω>0).若f (x )在区间⎣⎡⎦⎤π6,π2上具有单调性,且f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3=-f ⎝⎛⎭⎫π6,则f (x )的最小正周期为________. 答案 π解析 记f (x )的最小正周期为T . 由题意知T 2≥π2-π6=π3,又f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3=-f ⎝⎛⎭⎫π6, 且2π3-π2=π6, 可作出示意图如图所示(一种情况):∴x 1=⎝⎛⎭⎫π2+π6×12=π3, x 2=⎝⎛⎭⎫π2+2π3×12=7π12,∴T 4=x 2-x 1=7π12-π3=π4,∴T =π.★★★知能达标演练★★★一、选择题1.下列函数中最小正周期为π且图象关于直线x =π3对称的是( ) A .y =2sin ⎝⎛⎭⎫2x +π3 B .y =2sin ⎝⎛⎭⎫2x -π6 C .y =2sin ⎝⎛⎭⎫x 2+π3D .y =2sin ⎝⎛⎭⎫2x -π3 答案 B解析 函数y =2sin ⎝⎛⎭⎫2x -π6的周期T =2π2=π, 又sin ⎝⎛⎭⎫2×π3-π6=1, ∴函数y =2sin ⎝⎛⎭⎫2x -π6的图象关于直线x =π3对称. 2.(2018·广州质检)下列函数中,是周期函数的为( )A .y =sin|x |B .y =cos|x |C .y =tan|x |D .y =(x -1)0 答案 B解析 ∵cos|x |=cos x ,∴y =cos|x |是周期函数.3.函数f (x )=sin ⎝⎛⎭⎫2x -π4在区间⎣⎡⎦⎤0,π2上的最小值为( ) A .-1 B .-22 C.22 D .0 答案 B解析 由已知x ∈⎣⎡⎦⎤0,π2,得2x -π4∈⎣⎡⎦⎤-π4,3π4, 所以sin ⎝⎛⎭⎫2x -π4∈⎣⎡⎦⎤-22,1, 故函数f (x )=sin ⎝⎛⎭⎫2x -π4在区间⎣⎡⎦⎤0,π2上的最小值为-22.故选B. 4.函数y =sin x 2的图象是( )答案 D解析 函数y =sin x 2为偶函数,排除A ,C ;又当x =π2时函数取得最大值,排除B ,故选D.5.(2017·成都诊断)函数y =cos 2x -2sin x 的最大值与最小值分别为( )A .3,-1B .3,-2C .2,-1D .2,-2答案 D解析 y =cos 2x -2sin x =1-sin 2x -2sin x=-sin 2x -2sin x +1,令t =sin x ,则t ∈[-1,1],y =-t 2-2t +1=-(t +1)2+2,所以y max =2,y min =-2.6.已知函数f (x )=2sin(2x +φ)⎝⎛⎭⎫|φ|<π2的图象过点(0,3),则f (x )图象的一个对称中心是() A.⎝⎛⎭⎫-π3,0 B.⎝⎛⎭⎫-π6,0C.⎝⎛⎭⎫π6,0 D.⎝⎛⎭⎫π12,0答案 B解析 函数f (x )=2sin(2x +φ)⎝⎛⎭⎫|φ|<π2的图象过点(0,3),则f (0)=2sin φ=3,∴sin φ=32,又|φ|<π2,∴φ=π3,则f (x )=2sin ⎝⎛⎭⎫2x +π3,令2x +π3=k π(k ∈Z ),则x =k π2-π6(k ∈Z ),当k =0时,x =-π6,∴⎝⎛⎭⎫-π6,0是函数f (x )的图象的一个对称中心.7.(2017·衡水模拟)已知函数f (x )=⎪⎪⎪⎪tan ⎝⎛⎭⎫12x -π6,则下列说法正确的是( )A .f (x )的周期是π2B .f (x )的值域是{y |y ∈R ,且y ≠0}C .直线x =5π3是函数f (x )图象的一条对称轴D .f (x )的单调递减区间是⎝⎛⎦⎤2k π-2π3,2k π+π3,k ∈Z答案 D解析 函数f (x )的周期为2π,A 错;f (x )的值域为[0,+∞),B 错;当x =5π3时,12x -π6=2π3≠k π2,k ∈Z ,∴x =5π3不是f (x )的对称轴,C 错;令k π-π2<12x -π6≤k π,k ∈Z ,可得2k π-2π3<x ≤2k π+π3,k ∈Z ,∴f (x )的单调递减区间是⎝⎛⎦⎤2k π-2π3,2k π+π3,k ∈Z ,D 正确. 8.(2018·太原模拟)若f (x )=3sin x -4cos x 的一条对称轴方程是x =a ,则a 的取值范围可以是( )A.⎝⎛⎭⎫0,π4 B.⎝⎛⎭⎫π4,π2 C.⎝⎛⎭⎫π2,3π4D.⎝⎛⎭⎫3π4,π答案 D解析 因为f (x )=3sin x -4cos x =5sin(x -φ)⎝⎛⎭⎫其中tan φ=43且0<φ<π2,则sin(a -φ)=±1, 所以a -φ=k π+π2,k ∈Z ,即a =k π+π2+φ,k ∈Z ,而tan φ=43且0<φ<π2,所以π4<φ<π2,所以k π+3π4<a <k π+π,k ∈Z ,取k =0,此时a ∈⎝⎛⎭⎫3π4,π,故选D. 9.已知函数f (x )=2cos(ωx +φ)+b 对任意实数x 有f ⎝⎛⎭⎫x +π4=f (-x )恒成立,且f ⎝⎛⎭⎫π8=1,则实数b 的值为( )A .-1B .3C .-1或3D .-3 答案 C解析 由f ⎝⎛⎭⎫x +π4=f (-x )可知函数f (x )=2cos(ωx +φ)+b 关于直线x =π8对称,又函数f (x )在对称轴处取得最值,故±2+b =1,∴b =-1或b =3.二、填空题10.函数f (x )=cos ⎝⎛⎭⎫2x +π4的最小正周期是________. 答案 π11. y =3sin ⎝⎛⎭⎫2x -π6在区间⎣⎡⎦⎤0,π2上的值域是________. 答案 ⎣⎡⎦⎤-32,3 解析 当x ∈⎣⎡⎦⎤0,π2时,2x -π6∈⎣⎡⎦⎤-π6,5π6, sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤-12,1,故3sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤-32,3, 即y =3sin ⎝⎛⎭⎫2x -π6的值域为⎣⎡⎦⎤-32,3. 12. y =tan 2x 的定义域是________.答案 ⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2+π4,k ∈Z 解析 由2x ≠k π+π2,k ∈Z ,得x ≠k π2+π4,k ∈Z , ∴y =tan 2x 的定义域是⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2+π4,k ∈Z . 13.函数f (x )=4sin ⎝⎛⎭⎫π3-2x 的单调递减区间是______________________. 答案 ⎣⎡⎦⎤k π-π12,k π+512π(k ∈Z ) 解析 f (x )=4sin ⎝⎛⎭⎫π3-2x =-4sin ⎝⎛⎭⎫2x -π3. 所以要求f (x )的单调递减区间,只需求y =4sin ⎝⎛⎭⎫2x -π3的单调递增区间. 由-π2+2k π≤2x -π3≤π2+2k π(k ∈Z ),得 -π12+k π≤x ≤512π+k π(k ∈Z ). 所以函数f (x )的单调递减区间是⎣⎡⎦⎤-π12+k π,512π+k π(k ∈Z ). 14.cos 23°,sin 68°,cos 97°的大小关系是________. 答案 sin 68°>cos 23°>cos 97°解析 sin 68°=cos 22°,又y =cos x 在[0°,180°]上是减函数,∴sin 68°>cos 23°>cos 97°.15.函数y =cos ⎝⎛⎭⎫π4-2x 的单调递减区间为__________.答案 ⎣⎡⎦⎤k π+π8,k π+5π8(k ∈Z ) 解析 因为y =cos ⎝⎛⎭⎫π4-2x =cos ⎝⎛⎭⎫2x -π4, 所以令2k π≤2x -π4≤2k π+π(k ∈Z ), 解得k π+π8≤x ≤k π+5π8(k ∈Z ),所以函数的单调递减区间为⎣⎡⎦⎤k π+π8,k π+5π8(k ∈Z ). 16.(2018·福州质检)函数y =cos 2x +sin x ⎝⎛⎭⎫|x |≤π4的最小值为____________. 答案 1-22解析 令t =sin x ,∵|x |≤π4,∴t ∈⎣⎡⎦⎤-22,22. ∴y =-t 2+t +1=-⎝⎛⎭⎫t -122+54, ∴当t =-22时,y min =1-22. 17.已知函数f (x )=2sin ⎝⎛⎭⎫ωx -π6+1(x ∈R )的图象的一条对称轴为x =π,其中ω为常数,且ω∈(1,2),则函数f (x )的最小正周期为________.答案 6π5解析 由函数f (x )=2sin ⎝⎛⎭⎫ωx -π6+1(x ∈R )的图象的一条对称轴为x =π,可得ωπ-π6=k π+π2,k ∈Z ,∴ω=k +23,又ω∈(1,2),∴ω=53, 从而得函数f (x )的最小正周期为2π53=6π5. 18.(2018·珠海模拟)设函数f (x )=3sin ⎝⎛⎭⎫π2x +π4,若存在这样的实数x 1,x 2,对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为________. 答案 2解析 |x 1-x 2|的最小值为函数f (x )的半个周期,又T =4,∴|x 1-x 2|的最小值为2.19.已知关于x 的方程2sin ⎝⎛⎭⎫x +π6+1-a =0在区间⎣⎡⎦⎤0,2π3上存在两个根,则实数a 的取值范围是________.答案 [2,3)解析 sin ⎝⎛⎭⎫x +π6=a -12在⎣⎡⎦⎤0,2π3上存在两个根,设x +π6=t ,则t ∈⎣⎡⎦⎤π6,5π6, ∴y =sin t ,t ∈⎣⎡⎦⎤π6,5π6的图象与直线y =a -12有两个交点,∴12≤a -12<1,∴2≤a <3. 三、解答题20.已知f (x )=2sin ⎝⎛⎭⎫2x +π4. (1)求函数f (x )图象的对称轴方程;(2)求f (x )的单调递增区间;(3)当x ∈⎣⎡⎦⎤π4,3π4时,求函数f (x )的最大值和最小值.解 (1)f (x )=2sin ⎝⎛⎭⎫2x +π4, 令2x +π4=k π+π2,k ∈Z , 得x =k π2+π8,k ∈Z . 所以函数f (x )图象的对称轴方程是x =k π2+π8,k ∈Z . (2)令2k π-π2≤2x +π4≤2k π+π2,k ∈Z , 得k π-3π8≤x ≤k π+π8,k ∈Z . 故f (x )的单调递增区间为⎣⎡⎦⎤k π-3π8,k π+π8,k ∈Z . (3)当x ∈⎣⎡⎦⎤π4,3π4时,3π4≤2x +π4≤7π4, 所以-1≤sin ⎝⎛⎭⎫2x +π4≤22, 所以-2≤f (x )≤1,所以当x ∈⎣⎡⎦⎤π4,3π4时,函数f (x )的最大值为1,最小值为- 2.21. (2017·武汉调研)已知函数f (x )=a ⎝⎛⎭⎫2cos 2x 2+sin x +b . (1)若a =-1,求函数f (x )的单调增区间;(2)当x ∈[0,π]时,函数f (x )的值域是[5,8],求a ,b 的值. 解 f (x )=a (1+cos x +sin x )+b=2a sin ⎝⎛⎭⎫x +π4+a +b . (1)当a =-1时,f (x )=-2sin ⎝⎛⎭⎫x +π4+b -1, 由2k π+π2≤x +π4≤2k π+3π2(k ∈Z ), 得2k π+π4≤x ≤2k π+5π4(k ∈Z ), ∴f (x )的单调增区间为⎣⎡⎦⎤2k π+π4,2k π+5π4(k ∈Z ).(2)∵0≤x ≤π,∴π4≤x +π4≤5π4, ∴-22≤sin ⎝⎛⎭⎫x +π4≤1.依题意知a ≠0, ①当a >0时,⎩⎨⎧ 2a +a +b =8,b =5,∴a =32-3,b =5; ②当a <0时,⎩⎨⎧b =8,2a +a +b =5,∴a =3-32,b =8. 综上所述,a =32-3,b =5或a =3-32,b =8.22.(2018·兰州模拟)已知a >0,函数f (x )=-2a sin ⎝⎛⎭⎫2x +π6+2a +b ,当x ∈⎣⎡⎦⎤0,π2时, -5≤f (x )≤1.(1)求常数a ,b 的值;(2)设g (x )=f ⎝⎛⎭⎫x +π2且lg g (x )>0,求g (x )的单调区间. 解 (1)∵x ∈⎣⎡⎦⎤0,π2,∴2x +π6∈⎣⎡⎦⎤π6,7π6, ∴sin ⎝⎛⎭⎫2x +π6∈⎣⎡⎦⎤-12,1, ∴-2a sin ⎝⎛⎭⎫2x +π6∈[-2a ,a ], ∴f (x )∈[b,3a +b ],又∵-5≤f (x )≤1,∴b =-5,3a +b =1,因此a =2,b =-5.(2)由(1)得f (x )=-4sin ⎝⎛⎭⎫2x +π6-1, g (x )=f ⎝⎛⎭⎫x +π2=-4sin ⎝⎛⎭⎫2x +7π6-1 =4sin ⎝⎛⎭⎫2x +π6-1, 又由lg g (x )>0,得g (x )>1,∴4sin ⎝⎛⎭⎫2x +π6-1>1,∴sin ⎝⎛⎭⎫2x +π6>12, ∴2k π+π6<2x +π6<2k π+5π6,k ∈Z , 其中当2k π+π6<2x +π6≤2k π+π2,k ∈Z 时, g (x )单调递增,即k π<x ≤k π+π6,k ∈Z , ∴g (x )的单调增区间为⎝⎛⎦⎤k π,k π+π6,k ∈Z .又∵当2k π+π2<2x +π6<2k π+5π6,k ∈Z 时, g (x )单调递减,即k π+π6<x <k π+π3,k ∈Z . ∴g (x )的单调减区间为⎝⎛⎭⎫k π+π6,k π+π3,k ∈Z . ∴g (x )的单调增区间为⎝⎛⎦⎤k π,k π+π6,k ∈Z , 单调减区间为⎝⎛⎭⎫k π+π6,k π+π3,k ∈Z .。
江苏专用高考数学一轮复习考点17三角函数的图像与性质必刷题含解析1.(江苏省苏北四市2019届高三第一学期期末考试考前模拟)将函数()的图象向左平移个单位长度后,所得图象关于直线对称,则的最小值为______.【答案】【解析】将函数f(x)=sin(ωx)(ω>0)的图象向左平移个单位后,可得函数y=sin(ωx)的图象,再根据所得图象关于直线x=π对称,可得ωπkπ,k∈Z,∴当k=0时,ω取得最小值为,故答案为:.2.(江苏省清江中学2019届高三第二次教学质量调研)将函数的图像向右平移个单位,得到函数的图像,则函数在区间上的值域____________.【答案】【解析】由题得y=g(x)=,因为,所以.所以函数y=g(x)的值域为.故答案为:3.(盐城市2019届高三年级第一学期期中模拟考试)已知函数的最小正周期为4,则=________.【答案】【解析】由周期计算公式可得,解得=4.(苏省苏州市2019届高三高考模拟最后一卷)设函数()sin(2)3f x x π=+,若120x x <,且12()()0f x f x +=,则21x x -的取值范围是_______.【答案】(3π,+∞) 【解析】不妨设120x x <<,则2121x x x x -=-,由图可知210()33x x ππ->--=.故答案为:(3π,+∞) 5.(江苏省苏锡常镇四市2019届高三教学情况调查二)函数()cos()(0)3f x x πωω=->的图像关于直线2x π=对称,则ω的最小值为_______.【答案】23【解析】因为函数()cos (0)3f x x πωω⎛⎫=-> ⎪⎝⎭的图像关于直线2x π=对称, 所以cos 123ππω⎛⎫⨯-=± ⎪⎝⎭,所以()23k k Z ππωπ⨯-=∈. 解得:()223k k Z ω=+∈,又0>ω, 所以当0k =时,ω最小且为236.(江苏省2019届高三第二学期联合调研测)函数()sin()(0,0)f x A x A ωϕω=+>>的图象如图所示,则(0)(1)(2)...(2019)f f f f ++++的值为_____.【答案】222+ 【解析】观察图像易知2A =,8T =,4πω=,0ϕ=所以()2sin4f x x π=所以()()040f f ==,()()132f f ==,()22f =,()()572f f ==-,()62f =-所以()()()0170f f f +++=因为2019除以8余3 所以()()()()()()()()012201901230227222f f f f f f f f ++++=++++⨯=+故答案为:222+7.(江苏省苏州市2019届高三下学期阶段测试)已知函数sin()(0,0,||)y A x A ωϕωϕπ=+>><的图象如图所示,则该函数的解析式是__________.【答案】2sin 26y x π⎛⎫=+ ⎪⎝⎭【解析】根据图象可以看出A =2, 图像过(0,1)∴2sinφ=1,故φπ6=∵函数的图象过点(7π12-,0)所以7ππω126-+=2kππ+,k∈Z,故125ω2k76⎛⎫=-+⎪⎝⎭, k∈Z由题7π3,2124T T<<即1812ω77>>故当k=-1,ω2=∴函数的解析式是πy2sin2x6⎛⎫=+⎪⎝⎭.故答案为πy2sin2x6⎛⎫=+⎪⎝⎭8.(江苏省南京市、盐城市2019届高三第二次模拟考试)在中,若,则的最大值为______.【答案】【解析】在△ABC中,有,所以==,当即时取等.故答案为:9.(江苏省南京市、盐城市2019届高三第二次模拟考试)若函数的图象经过点,且相邻两条对称轴间的距离为,则的值为______.【答案】【解析】因为相邻两条对称轴间的距离为,所以所以.因为函数的图象经过点所以.所以,所以.故答案为:10.(江苏省南通市基地学校2019届高三3月联考)已知角的终边经过点,函数图象的相邻两条对称轴之间的距离等于,则的值为____.【答案】【解析】角终边经过点,两条相邻对称轴之间距离为即本题正确结果:11.(江苏省无锡市2019届高三上学期期末考试)已知直线与函数的图象恰有四个公共点,,,,则__________.【答案】-2【解析】直线y=a(x+2)过定点(-2,0),如下图所示,由图可知,直线与余弦函数图象在x4处相切,且∈,即a(x4+2)=-cos,所以,a=又,即直线的斜率为:a=,因此a==,即+=+=--2=-2.故答案为:-2.12.(江苏省镇江市2019届高三考前三模)若函数()2sin()f x x ωϕ=+ (01ω<<,02πϕ<<)的图像过点3),且关于点(2,0)-对称,则(1)f -=_______. 【答案】1 【解析】函数()()2sin f x x ωϕ=+的图像过点(3 2sin 3ϕ∴=3sin 2ϕ=02πϕ<<3πϕ∴=又函数图象关于点()2,0-对称 2sin 203πω⎛⎫∴-+= ⎪⎝⎭,即:23k πωπ-+=,k Z ∈ 126k πωπ∴=-+,k Z ∈01ω<< 6πω∴= ()2sin 63f x x ππ⎛⎫∴=+ ⎪⎝⎭,()12sin 2sin 1636f πππ⎛⎫∴-=-+== ⎪⎝⎭13.(江苏省南通市2019届高三模拟练习卷四模)已知函数()sin()f x x ωϕ=+(0>ω,π2<ϕ)的图象关于直线π6x =对称,两个相邻的最高点之间的距离为2π. (1)求()f x 的解析式; (2)在△ABC 中,若3()5f A =-,求sin A 的值. 【答案】(1)()πsin 3f x x ⎛⎫=+ ⎪⎝⎭;(2433-. 【解析】(1)∵函数()sin()f x x ωϕ=+(ω>0,π2<ϕ)的图象上相邻两个最高点的距离为2π, ∴函数的周期T =2π,∴2πω=2π,解得ω=1,∴f (x )=sin (x+φ),又∵函数f (x )的图象关于直线π6x =对称,∴62k ππϕπ+=+,k ∈Z , ∵π2<ϕ,∴ϕ=3π,∴f (x )=sin (x+3π).(2)在△ABC 中,∵3()5f A =-,A ∈(0,π),∴3sin 035A π⎛⎫+=-< ⎪⎝⎭,∴244,,cos 1sin 33335A A A πππππ⎛⎫⎛⎫⎛⎫+∈∴+=--+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ∴sin sin ()sin cos cos()sin 333333A A A A ππππππ⎡⎤⎛⎫=+-=+-+ ⎪⎢⎥⎣⎦⎝⎭3143433525210-⎛⎫⎛⎫=-⨯--⨯=⎪ ⎪⎝⎭⎝⎭. 14.(江苏省苏州市2019届高三高考模拟最后一卷)选修4-4:极坐标与参数方程:在直角坐标系xOy 中,以坐标原点O 为极点,以x 轴正半轴为极轴,建立极坐标系,直线l 的极坐标方程为(3cos )43sm ρθθ+=设点P 是曲线22:19y C x +=上的动点,求P 到直线l 距离的最大值.【答案】33【解析】直线:3430l x y +-= 设点(cos ,3sin )P αα,∴|3sin 3cos 43|d αα+-=23sin 436|2343|332πα⎛⎫+- ⎪--⎝⎭== 当且仅当262k ππαπ+=-,即223k αππ=-∈,(k Z)时取“=”所以P 到直线l 距离的最大值为33.15.(江苏省南京市、盐城市2019届高三第二次模拟考试)某公园内有一块以为圆心半径为米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形区域,其中两个端点,分别在圆周上;观众席为梯形内切在圆外的区域,其中,,且,在点的同侧.为保证视听效果,要求观众席内每一个观众到舞台处的距离都不超过米.设,.问:对于任意,上述设计方案是否均能符合要求?【答案】能符合要求【解析】过作垂直于,垂足为.在直角三角形中,,,所以,因此.由图可知,点处观众离点处最远.在三角形中,由余弦定理可知.因为,所以当时,即时,,即.因为,所以观众席内每一个观众到舞台处的距离都不超过米.答:对于任意,上述设计方案均能符合要求.16.(江苏省扬州市2018-2019学年度第一学期期末检测试题)已知函数,.(1)求函数的单调增区间;(2)求方程在(0,]内的所有解.【答案】(1),;(2)或【解析】(1)由,,解得:,.∴函数的单调增区间为,(2)由得,解得:,即,∵,∴或.17.(江苏省如皋市2019届高三教学质量调研三)在中,,.(1)求角的大小;(2)设,其中,求取值范围.【答案】(1);(2).【解析】(1)因为,所以,所以,又因为,所以,解得,由余弦定理得,因为,所以.(2),因为,所以,所以取值范围为.18.(江苏省苏州市2018届高三调研测试)已知函数.(1)求函数的最小值,并写出取得最小值时自变量x的取值集合;(2)若,求函数的单调增区间.【答案】(1)取得最小值0,(2)单调增区间是和.【解析】(1).当,即时,取得最小值0.此时,取得最小值时自变量x的取值集合为.(2)因为,令,解得,又,令,,令,,所以函数在的单调增区间是和.19.(江苏省清江中学2018届高三学情调研考试)已知函数.(1)求的单调递增区间;(2)求在区间上的最小值.【答案】(I),;(II).【解析】(I).由得,,则的单调递增区间为,.(II)∵,∴,当,时,.1。