2020年中考数学复习每日一练 第二十九讲 《图形的对称》(含答案)

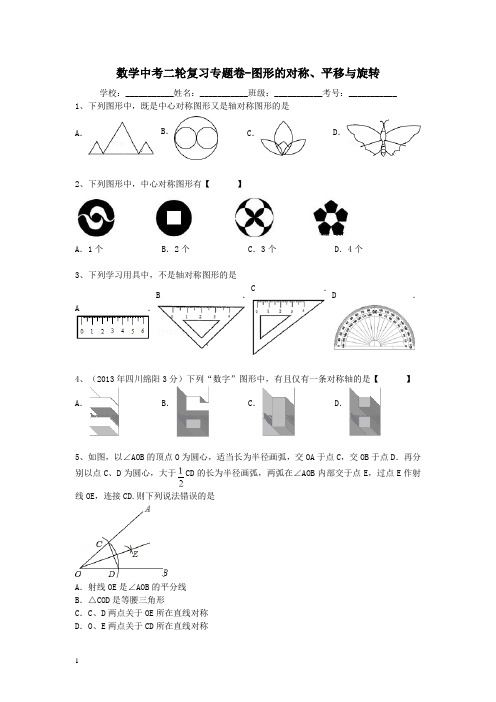
数学中考二轮复习专题卷-图形的对称、平移与旋转学校：___________姓名：___________班级：___________考号：___________ 1、下列图形中，既是中心对称图形又是轴对称图形的是 A ．B ．C ．D ．2、下列图形中，中心对称图形有【 】A ．1个B ．2个C ．3个D ．4个3、下列学习用具中，不是轴对称图形的是A．B ．C．D．4、（2013年四川绵阳3分）下列“数字”图形中，有且仅有一条对称轴的是【 】 A ．B ．C ．D ．5、如图，以∠AOB 的顶点O 为圆心，适当长为半径画弧，交OA 于点C ，交OB 于点D ．再分别以点C 、D 为圆心，大于CD 的长为半径画弧，两弧在∠AOB 内部交于点E ，过点E 作射线OE ，连接CD.则下列说法错误的是A ．射线OE 是∠AOB 的平分线 B ．△COD 是等腰三角形C ．C 、D 两点关于OE 所在直线对称 D ．O 、E 两点关于CD 所在直线对称6、（2013年四川攀枝花3分）如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC 绕点A旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′=【】A．30°B．35°C．40°D．50°7、下列图形中,不是轴对称图形的是A．B．C．D．8、如图，正方形地砖的图案是轴对称图形，该图形的对称轴有A．1条B．2条C．4条D．8条9、下列四种图形都是轴对称图形，其中对称轴条数最多的图形是A．等边三角形B．矩形C．菱形D．正方形10、下列图案中，既是轴对称图形又是中心对称图形的是【】A．B．C．D．11、在如图所示的单位正方形网格中，△ABC经过平移后得到△A1B1C1，已知在AC上一点P （2.4，2）平移后的对应点为P1，点P1绕点O逆时针旋转180°，得到对应点P2，则P2点的坐标为A．（1.4，－1）B．（1.5，2）C．（1.6，1）D．（2.4，1）12、下列图形：其中所有轴对称图形的对称轴条数之和为A．13 B．11 C．10 D．813、P是∠AOB内一点，分别作点P关于直线OA、OB的对称点P1、P2，连接OP1、OP2，则下列结论正确的是A．OP1⊥OP2 B．OP1=OP2 C．OP1⊥OP2且OP1=O P2 D．OP1≠OP214、如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE．若∠CAE=65°，∠E=70°，且AD⊥BC，∠BAC的度数为A．60°B．75°C．85°D．90°15、在下列图形中既是轴对称图形又是中心对称图形的是A．角B．线段C．等腰三角形D．平行四边形16、下列命题中，真命题是【】A．位似图形一定是相似图形B．等腰梯形既是轴对称图形又是中心对称图形C．四条边相等的四边形是正方形D．垂直于同一直线的两条直线互相垂直17、如图，将边长为1cm的等边三角形ABC沿直线l向右翻动（不滑动），点B从开始到结束，所经过路径的长度为A．B．C．D．3cm18、如图（1），已知两个全等三角形的直角顶点及一条直角边重合。

考点三十二：图形的轴对称1．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴．把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点．2．图形轴对称的性质如果两个图形关于某条直线对称，那么对称轴是任意一对对应点所连线段的垂直平分线．轴对称图形的对称轴，是任意一对对应点所连线段的垂直平分线．对应线段、对应角相等．3．由一个平面图形可以得到它关于一条直线l对称的图形，这个图形与原图形的形状、大小完全一样；新图形上的每一点，都是原图形上的某一点关于直线l的对称点；连接任意一对对应点的线段被对称轴垂直平分．这样，由一个平面图形得到它的轴对称图形叫做轴对称变换．一个轴对称图形可以看作以它的一部分为基础，经轴对称变换而成．4. 轴对称与轴对称图形轴对称图形和图形的轴对称之间的的区别是：轴对称图形是一个具有特殊性质的图形，而图形的轴对称是说两个图形之间的位置关系；两者之间的联系是：若把轴对称的两个图形视为一个整体，则它就是一个轴对称图形；若把轴对称图形在对称轴两旁的部分视为两个图形，则这两个图形就形成轴对称的位置关系．中考数学模拟试卷一、选择题（本题包括10个小题，每小题只有一个选项符合题意）1．我国古代数学著作《孙子算经》中有“多人共车”问题：今有三人共车，二车空；二人共车，九人步．问人与车各几何？其大意是：每车坐3人，两车空出来；每车坐2人，多出9人无车坐. 问人数和车数各多少？设车x 辆，根据题意，可列出的方程是 ( )．A ．3229x x -=+B ．3(2)29x x -=+C ．2932x x +=- D ．3(2)2(9)x x -=+ 【答案】B【解析】根据题意，表示出两种方式的总人数，然后根据人数不变列方程即可.【详解】根据题意可得：每车坐3人，两车空出来，可得人数为3（x-2）人；每车坐2人，多出9人无车坐，可得人数为（2x+9）人，所以所列方程为：3（x-2）=2x+9.故选B.【点睛】此题主要考查了一元一次方程的应用，关键是找到问题中的等量关系：总人数不变，列出相应的方程即可.2．若点A （1+m ，1﹣n ）与点B （﹣3，2）关于y 轴对称，则m+n 的值是（ ）A ．﹣5B ．﹣3C ．3D ．1【答案】D【解析】根据关于y 轴的对称点的坐标特点：横坐标互为相反数，纵坐标不变，据此求出m 、n 的值，代入计算可得．【详解】∵点A （1+m ，1﹣n ）与点B （﹣3，2）关于y 轴对称，∴1+m=3、1﹣n=2，解得：m=2、n=﹣1，所以m+n=2﹣1=1，故选D ．【点睛】本题考查了关于y 轴对称的点，熟练掌握关于y 轴对称的两点的横坐标互为相反数，纵坐标不变是解题的关键.3．若分式有意义，则x 的取值范围是（ ） A ．x ＞3B ．x ＜3C ．x≠3D ．x=3 【答案】C【解析】试题分析：∵分式13x -有意义，∴x﹣3≠0，∴x≠3；故选C ． 考点：分式有意义的条件．4．要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划7天，每天安排4场比赛.设比赛组织者应邀请x 个队参赛，则x 满足的关系式为（）A ．1(1)282x x -=B ．1(1)282x x +=C ．(1)28x x -=D ．(1)28x x +=【答案】A【解析】根据应用题的题目条件建立方程即可.【详解】解：由题可得：1(1)472x x -=⨯ 即：1(1)282x x -= 故答案是：A.【点睛】本题主要考察一元二次方程的应用题，正确理解题意是解题的关键.5．如图，等腰直角三角形ABC 位于第一象限，2AB AC ==，直角顶点A 在直线y x =上，其中点A 的横坐标为1，且两条直角边AB ，AC 分别平行于x 轴、y 轴，若反比例函数k y x=的图象与ABC △有交点，则k 的取值范围是（ ）．A ．12k <<B ．13k ≤≤C ．14k ≤<D ．14k ≤≤【答案】D 【解析】设直线y=x 与BC 交于E 点，分别过A 、E 两点作x 轴的垂线，垂足为D 、F ，则A （1，1），而AB=AC=2，则B （3，1），△ABC 为等腰直角三角形，E 为BC 的中点，由中点坐标公式求E 点坐标，当双曲线与△ABC 有唯一交点时，这个交点分别为A 、E ，由此可求出k 的取值范围.解：∵2AC BC ==，90CAB ∠=︒．()1,1A ．又∵y x =过点A ，交BC 于点E ，∴2EF ED ==， ∴()2,2E ，∴14k ≤≤．故选D.6．共享单车已经成为城市公共交通的重要组成部分，某共享单车公司经过调查获得关于共享单车租用行驶时间的数据，并由此制定了新的收费标准：每次租用单车行驶a 小时及以内，免费骑行；超过a 小时后，每半小时收费1元，这样可保证不少于50%的骑行是免费的．制定这一标准中的a 的值时，参考的统计量是此次调查所得数据的（ ）A ．平均数B ．中位数C ．众数D ．方差【答案】B 【解析】根据需要保证不少于50%的骑行是免费的，可得此次调查的参考统计量是此次调查所得数据的中位数.【详解】因为需要保证不少于50%的骑行是免费的，所以制定这一标准中的a 的值时，参考的统计量是此次调查所得数据的中位数，故选B ．【点睛】本题考查了中位数的知识，中位数是以它在所有标志值中所处的位置确定的全体单位标志值的代表值，不受分布数列的极大或极小值影响，从而在一定程度上提高了中位数对分布数列的代表性。

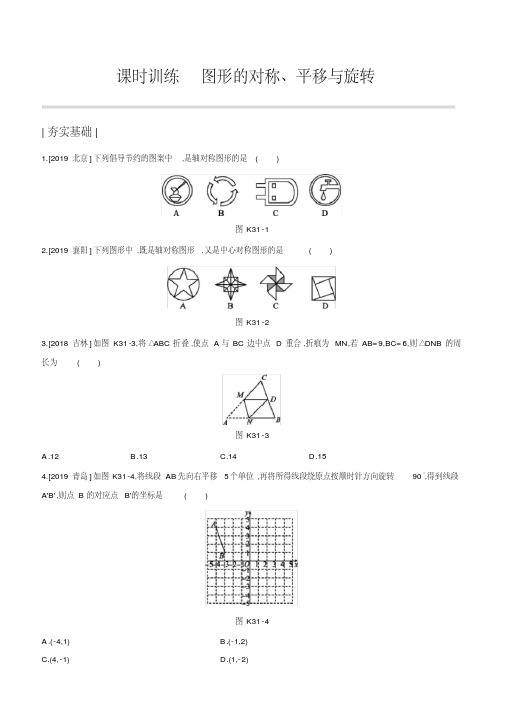
课时训练图形的对称、平移与旋转|夯实基础|1.[2019·北京]下列倡导节约的图案中,是轴对称图形的是()图K31-12.[2019·襄阳]下列图形中,既是轴对称图形,又是中心对称图形的是()图K31-23.[2018·吉林]如图K31-3,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为()图K31-3A.12B.13C.14D.154.[2019·青岛]如图K31-4,将线段AB先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段A'B',则点B的对应点B'的坐标是()图K31-4A.(-4,1)B.(-1,2)线段AP与EF的交点Q处,BC=4√3,则线段AB的长是()图K31-5A.8B.8√2C.8√3D.106.[2019·随州]如图K31-6,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为.图K31-67.[2017·东营]如图K31-7,已知菱形ABCD的周长为16,面积为8√3,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为.图K31-78.[2019·河池]如图K31-8,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.图K31-89.[2019·淮安]如图K31-9,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连结AP,则tan∠HAP=.线段AP与EF的交点Q处,BC=4√3,则线段AB的长是()图K31-5A.8B.8√2C.8√3D.106.[2019·随州]如图K31-6,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为.图K31-67.[2017·东营]如图K31-7,已知菱形ABCD的周长为16,面积为8√3,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为.图K31-78.[2019·河池]如图K31-8,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.图K31-89.[2019·淮安]如图K31-9,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连结AP,则tan∠HAP=.图K31-9线段AP与EF的交点Q处,BC=4√3,则线段AB的长是()图K31-5A.8B.8√2C.8√3D.106.[2019·随州]如图K31-6,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为.图K31-67.[2017·东营]如图K31-7,已知菱形ABCD的周长为16,面积为8√3,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为.图K31-78.[2019·河池]如图K31-8,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.图K31-89.[2019·淮安]如图K31-9,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连结AP,则tan∠HAP=.图K31-9线段AP与EF的交点Q处,BC=4√3,则线段AB的长是()图K31-5A.8B.8√2C.8√3D.106.[2019·随州]如图K31-6,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为.图K31-67.[2017·东营]如图K31-7,已知菱形ABCD的周长为16,面积为8√3,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为.图K31-78.[2019·河池]如图K31-8,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.图K31-89.[2019·淮安]如图K31-9,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连结AP,则tan∠HAP=.图K31-9线段AP与EF的交点Q处,BC=4√3,则线段AB的长是()图K31-5A.8B.8√2C.8√3D.106.[2019·随州]如图K31-6,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为.图K31-67.[2017·东营]如图K31-7,已知菱形ABCD的周长为16,面积为8√3,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为.图K31-78.[2019·河池]如图K31-8,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.图K31-89.[2019·淮安]如图K31-9,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连结AP,则tan∠HAP=.图K31-9线段AP与EF的交点Q处,BC=4√3,则线段AB的长是()图K31-5A.8B.8√2C.8√3D.106.[2019·随州]如图K31-6,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为.图K31-67.[2017·东营]如图K31-7,已知菱形ABCD的周长为16,面积为8√3,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为.图K31-78.[2019·河池]如图K31-8,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.图K31-89.[2019·淮安]如图K31-9,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连结AP,则tan∠HAP=.图K31-9线段AP与EF的交点Q处,BC=4√3,则线段AB的长是()图K31-5A.8B.8√2C.8√3D.106.[2019·随州]如图K31-6,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为.图K31-67.[2017·东营]如图K31-7,已知菱形ABCD的周长为16,面积为8√3,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为.图K31-78.[2019·河池]如图K31-8,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.图K31-89.[2019·淮安]如图K31-9,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连结AP,则tan∠HAP=.图K31-9线段AP与EF的交点Q处,BC=4√3,则线段AB的长是()图K31-5A.8B.8√2C.8√3D.106.[2019·随州]如图K31-6,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为.图K31-67.[2017·东营]如图K31-7,已知菱形ABCD的周长为16,面积为8√3,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为.图K31-78.[2019·河池]如图K31-8,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.图K31-89.[2019·淮安]如图K31-9,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连结AP,则tan∠HAP=.图K31-9线段AP与EF的交点Q处,BC=4√3,则线段AB的长是()图K31-5A.8B.8√2C.8√3D.106.[2019·随州]如图K31-6,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为.图K31-67.[2017·东营]如图K31-7,已知菱形ABCD的周长为16,面积为8√3,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为.图K31-78.[2019·河池]如图K31-8,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.图K31-89.[2019·淮安]如图K31-9,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连结AP,则tan∠HAP=.图K31-9。

2024年中考数学二轮复习模块专练—轴对称和中心对称（含答案）一、轴对称1．轴对称图形的定义：一个图形沿着某直线折叠，直线两旁的部分能完全重合，这个图形就叫做轴对称图形，该直线就是它的对称轴．2．轴对称：对于两个图形，如果沿一条直线对折后，它们能够完全重合，那么这两个图形关于这条直线成轴对称．3．轴对称的性质（1）对应线段相等，对应角相等；（2）对应点所连的线段被对称轴垂直平分；4．轴对称作图（1）找出图形中的关键点；（2）作关键点的对称点：一垂二延三相等；（3）连接关键点；二、中心对称1．中心对称定义：如果把一个图形绕着某一点旋转180°，它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做它们的对称中心．2．中心对称图形定义：把一个图形绕某个点旋转180°如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心．区别：中心对称→两个图形的关系，中心对称图形→一种图形的特征．3．中心对称性质：成中心对称的两个图形中，对应点所连线段经过对称中心，且被对试卷第2页，共12页称中心平分．同心对称具有旋转的性质．4．中心对称图形作图（1）找出图形中的关键点；（2）作关键点的对称点：一连（关键点与对称中心连接）二延三相等；（3）连接关键点；《义务教育数学课程标准》2022年版，学业质量要求：1．理解轴对称和中心对称的概念；2．知道轴对称和中心对称的性质；3．会用轴对称和中心对称的运动认识、理解和表达现实世界中相应的现象；4．理解几何图形的对称性，感悟现实世界中的对称美，知道可以用数学语言表达对称；【例1】（2023·青海西宁·统考中考真题）1．河湟剪纸被列入青海省第三批省级非物质文化遗产名录，是青海劳动人民结合河湟文化，创造出独具高原特色的剪纸．以下剪纸图案既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D．【变1】（2023·山东青岛·统考中考真题）2．生活中有许多对称美的图形，下列是中心对称图形但不是轴对称图形的是（）A．B．C．D．【例1】（2023·河北沧州·统考二模）的3．如图由66⨯个边长为1的小正方形组成，每个小正方形的顶点称为格点，ABC绕着点O顺时针三个顶点A，B，C均在格点上，O是AC与网格线的交点，将ABC旋转180︒．以下是嘉嘉和淇淇得出的结论，下列判断正确的是（）嘉嘉：旋转后的三角形的三个顶点均在格点上；淇淇：旋转前后两个三角形可形成平行四边形A．只有嘉嘉对B．只有淇淇对C．两人都对D．两人都不对试卷第4页，共12页【例1】（2023·安徽亳州·校联考模拟预测）5．如图，在平面直角坐标系中，(1)作出ABC 关于y 轴对称的A B C ''' ；(2)作出ABC 关于点O 成中心对称的111A B C △；(3)在x 轴上找一点P ，使1PB PC =，并写出点P 的坐标．【变1】（2023·四川广安·统考中考真题）6．将边长为2的正方形剪成四个全等的直角三角形，用这四个直角三角形拼成符合要求的四边形，请在下列网格中画出你拼成的四边形（注：①网格中每个小正方形的边长为1；②所拼的图形不得与原图形相同；③四边形的各顶点都在格点上）．一、选择题（2023·江苏·统考中考真题）7．剪纸是中国优秀的传统文化．下列剪纸图案中，是轴对称图形的是（）．A．B．C．D．（2023·河北衡水·统考二模）8．三个全等的等边三角形按图1所示位置摆放，现添加一个大小相同的等边三角形，使四个等边三角形组成一个中心对称图形（如图2），则添加的等边三角形所放置的位置是（）A．①B．②C （2023·黑龙江·统考中考真题）9．如图，在平面直角坐标中，矩形ABCD的边直线OE折叠到如图所示的位置，线段OD恰好经过点A．()1,2B．(-二、填空题（2023·吉林长春·统考中考真题）10．如图，将正五边形纸片ABCDE试卷第6页，共12页（2023·黑龙江绥化·统考中考真题）的半径为2cm，12．如图，O翻折，使点C与圆心O重合，则阴影部分的面积为（2023·湖北武汉·统考中考真题）13．如图，DE平分等边交于,G H两点．若DG（2023·江苏扬州·统考中考真题）14．如图，已知正方形ABCD着EF翻折，点B恰好落在积比为3∶5，那么线段FC的长为（2023·江苏泰州·统考二模）15．如图，在平面直角坐标系中，B-，点D的交点，点(2,0)且D、F两点关于y轴上某点成中心对称，连接（2023·山东济南·统考中考真题）16．如图，将菱形纸片ABCD折痕CP交AD于点P．若三、解答题（2023·浙江温州·统考中考真题）试卷第8页，共12页(1)在图中画一个等腰三角形画出该三角形绕矩形ABCD△(2)在图中画一个Rt PQR角形向右平移1个单位后的图形．（2023·江西南昌·校考二模）18．如图，在矩形ABCD中，(1)在图1中作矩形ABCD关于点E成中心对称的图形．(2)在图2中作以E为顶点的矩形．（2023·湖北宜昌·统考中考真题）(1)画出线段OA绕点O顺时针旋转关于直线OB对称的图形，点(2)画出与AOB∠的度数为_________(3)填空：OCB试卷第10页，共12页（2023·山东枣庄·统考中考真题）20．（1）观察分析：在一次数学综合实践活动中，老师向同学们展示了图①，图②，图③三幅图形，请你结合自己所学的知识，观察图中阴影部分构成的图案，写出三个图案都具有的两个共同特征：___________，___________．（2）动手操作：请在图④中设计一个新的图案，使其满足你在（1）中发现的共同特征．（2023·江苏南通·统考一模）21．如图，矩形ABCD 中，63AB AD ==，．E 为边AB 上一动点，连接DE ．作AF D E ⊥交矩形ABCD 的边于点F ，垂足为G ．(1)求证：AFB DEA ∠=∠；(2)若1CF =，求AE 的长；(3)点O 为矩形ABCD 的对称中心，探究OG 的取值范围．（2023·江苏无锡·统考中考真题）22．如图，四边形ABCD 是边长为4的菱形，60A ∠=︒，点Q 为CD 的中点，P 为线段AB 上的动点，现将四边形PBCQ 沿PQ 翻折得到四边形PB C Q ''．(1)当45QPB ∠=︒时，求四边形BB C C ''的面积；(2)当点P 在线段AB 上移动时，设BP x =，四边形BB C C ''的面积为S ，求S 关于x 的函数表达式．（2023·内蒙古通辽·统考中考真题）23．综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动，有一位同学操作过程如下：操作一：对折正方形纸片ABCD ，使AD 与BC 重合，得到折痕EF ，把纸片展平；操作二：在AD 上选一点P ，沿BP 折叠，使点A 落在正方形内部点M 处，把纸片展平，连接PM 、BM ，延长PM 交CD 于点Q ，连接BQ ．(1)如图1，当点M 在EF 上时，EMB ∠=___________度；(2)改变点P 在AD 上的位置（点P 不与点A ，D 重合）如图2，判断MBQ ∠与CBQ ∠的数量关系，并说明理由．（2023·山东枣庄·统考中考真题）24．问题情境：如图1，在ABC 中，1730AB AC BC ===，，AD 是BC 边上的中线．如图2，将ABC 的两个顶点B ，C 分别沿,EF GH 折叠后均与点D 重合，折痕分别交,,AB AC BC 于点E ，G ，F ，H ．试卷第12页，共12页猜想证明：(1)如图2，试判断四边形AEDG 的形状，并说明理由．问题解决；(2)如图3，将图2中左侧折叠的三角形展开后，重新沿MN 折叠，使得顶点B 与点H 重合，折痕分别交,AB BC 于点M ，N ，BM 的对应线段交DG 于点K ，求四边形MKGA 的面积．参考答案：1．D【分析】根据轴对称图形和中心对称图形的特点逐项判断即可．【详解】解：A．是轴对称图形，不是中心对称图形，故该选项不符合题意；B．既不是轴对称图形，也不是中心对称图形，故该选项不符合题意；C．既不是轴对称图形，也不是中心对称图形，故该选项不符合题意；D．既是轴对称图形，又是中心对称图形，故该选项符合题意．故选D．【点睛】本题考查识别轴对称图形与中心对称图形．识别轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．识别中心对称图形是要寻找对称中心，旋转180度后与自身重合．2．D【分析】根据中心对称图形定义：把图形沿某点旋转180︒得到的新图形与原图形重合的图形叫中心对称图形，轴对称图形定义：把一个图形沿某条直线对折两边完全重合的图形叫轴对称图形，逐个判断即可得到答案．【详解】解：由题意可得，A选项图形即是中心对称图形又是轴对称图形，不符合题意，B选项图形即是中心对称图形又是轴对称图形，不符合题意，C选项图形即是中心对称图形又是轴对称图形，不符合题意，D选项图形是中心对称图形但不是轴对称图形，符合题意，故选：D；【点睛】本题考查中心对称图形定义：把图形沿某点旋转180︒得到的新图形与原图形重合的图形叫中心对称图形，轴对称图形定义：把一个图形沿某条直线对折两边完全重合的图形答案第2页，共28页叫轴对称图形．3．C【分析】画出旋转后的图形，根据图形解答．【详解】如图，取格点B '，连接OB '，OB ，取格点E ，F ．∵,,AEO CFO AOE COF AE CF ∠=∠∠=∠=，∴AOE COF △≌△，∴OA OF =，∴点A 关于点O 的对称点与点C 重合，点C 关于点O 的对称点与点A 重合．同理可证：点B 与点B '关于点O 对称，∴旋转后的三角形的三个顶点均在格点上，故嘉嘉说法正确；由中心对称的性质得A ABC B C '''≌△△，∴AB A B ''=，BC B C ''=，∴四边形ABA B ''是平行四边形，∴旋转前后两个三角形可形成平行四边形，故淇淇说法正确．故选C ．【点睛】本题考查了全等三角形的判定与性质，的关键．4．210【分析】取BC中点H，连接AH，取由折叠可知AD CD DE x===则DF=三角形中位线定理得到15BG=，从而推导出答案第4页，共28页答案第6页，共28页A B C '''∴△即为所求；（2）解：如图所示：111A B C ∴ 即为所求；（3）如图所示：1,0-．【点睛】本题考查作图﹣旋转变换，轴对称变换，熟练掌握基本作图知识是解题的关键．6．见解析（答案不唯一，符合题意即可）【分析】根据轴对称图形和中心对称图形的性质进行作图即可．【详解】解：①要求是轴对称图形但不是中心对称图形，则可作等腰梯形，如图四边形ABCD 即为所求；②要求是中心对称图形但不是轴对称图形，则可作一般平行四边形，如图四边形ABCD即为所求；③要求既是轴对称图形又是中心对称图形，则可作菱形、矩形等，如图四边形ABCD即为所求；④要求既不是轴对称图形又不是中心对称图形，则考虑作任意四边形，如图四边形ABCD即为所求．答案第8页，共28页【点睛】本题考查轴对称图形和中心对称图形的概念及作图，轴对称图形：把一个图形沿着某条直线折叠，能够与另一个图形重合；中心对称图形：把一个图形绕着某个点旋转180 能够和原图形重合．7．B【分析】根据轴对称图形的概念逐项分析判断即可，轴对称图形的概念：平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形．【详解】解：选项A 、C 、D 均不能找到这样的一条直线，使直线两旁的部分能够完全重合的图形，所以不是轴对称图形；选项B 能找到这样的一条直线，使直线两旁的部分能够完全重合的图形，所以是轴对称图形；故选：B ．【点睛】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．8．D【分析】根据中心对称图形的定义：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形可得答案．【详解】解：依题意，添加的等边三角形④，可得中心对称图形，【点睛】本题考查了矩形的判定和性质，理的应用等知识，通过证明三角形相似，10．45【分析】根据题意求得正五边形的每一个内角为'答案第10页，共28页∵将 AB 沿弦AB 翻折，使点∴AC AO =，OC AB⊥答案第12页，共28页答案第14页，共28页则90FGK DHK ∠=∠=︒，记FD 交y 轴于点K ，∵D 点与F 点关于y 轴上的∴KF KD =，答案第16页，共28页【点睛】本题主要考查了菱形的性质，折叠的性质，解直角三角形，解题的关键是熟练掌握菱形和折叠的性质，正确画出辅助线，构造直角三角形求解．17．(1)见解析(2)见解析答案第18页，共28页（2）画法不唯一，如图3或图4．【点睛】本题主要考查了格点作图，解题关键是掌握网格的特点，灵活画出相等的线段和互相垂直或平行的线段．18．(1)见解析；(2)见解析【分析】（1）连接AE 并延长至点M ，使得AE ME =；连接BE 并延长至点N ，使得BE NE =，连接DN 、MN 、CN ，即可得到矩形DCMN 为所求作；（2）连接AC 、BD ，交点为点O ，连接EO 并延长交AB 于点F ，根据中位线定理，得到EF AD BC ∥∥，即可得到矩形ADEF 或矩形BCEF 为所求作．【详解】（1）解：如图1中，矩形DCMN 即为所求；（2）解：如图2中，矩形ADEF 或矩形BCEF 即为所求．【点睛】本题考查了画中心对称图形，矩形的判定和性质，三角形中位线定理等知识，根据相关性质正确作图是解题关键．19．(1)详见解析(2)详见解析(3)45︒【分析】（1）根据题目叙述画出图形即可；（2）根据题目叙述画出图形即可；（3）由（1）作图可得AOB 是等腰直角三角形，且=45A ︒∠，由对称的性质可得45OCB ∠=︒．【详解】（1）在方格纸中画出线段OA 绕点O 顺时针旋转90︒后得到的线段OB ，连接AB ,如图；（2）画出与AOB 关于直线OB 对称的图形，点A 的对称点是C ；如上图所示：（3）由（1）作图可得AOB 是等腰直角三角形，且=45A ︒∠，再根据对称的性质可得45OCB A ∠=∠=︒．故答案为：45︒．【点睛】此题考查了旋转作图及作轴对称图形，解答本题的关键是仔细审题，得出旋转三要素，进而得出旋转后的图形．20．（1）观察发现四个图形都是轴对称图形，且面积相等；（2）见解析【分析】（1）应从对称方面，阴影部分的面积等方面入手思考；（2）应画出既是轴对称图形，且面积为4的图形．【点睛】此题主要考查了利用轴对称图形设计图案，关键是掌握利用轴对称的作图方法来作图，通过变换对称轴来得到不同的图案．21．(1)见解析答案第20页，共28页同（1）可证DAF DEA∠=∠tan tanDAF DEA∴∠=∠，∴DF ADAD AE=，即533AE=，95AE∴=，1 AE∴=或9 5；答案第22页，共28页则OG OH HG ≥-．90AGE AGD ∠=∠=︒ ，1322HG AD ∴==，∵点O 为矩形ABCD 的对称中心，∴点O 为AC 的中点．答案第24页，共28页答案第26页，共28页∵1122 CHGS CH HG=⋅=∴154302CG HE⋅=⨯=，平行四边形的判定和性质．熟练掌握相关知识点，并灵活运用，是解题的关键．答案第28页，共28页。

图形变换之对称 知识精讲 习题集中考内容中考要求A B C图形的轴对称了解图形的轴对称和轴对称图形，理解对应点所连的线段被对称轴垂直平分的性质 能按要求作出简单平面图形经过一次或两次轴对称后的图形；掌握简单图形之间的轴对称关系，并能指出对称轴；掌握基本图形（等腰三角形、矩形、菱形、等腰梯形、正多边形、圆）的轴对称性及其相关性质能运用轴对称的知识解决简单问题⎧⎪⎧⎪⎪⎪⎨⎪⎨⎪⎪⎪⎪⎪⎩⎩轴对称垂直平分线对称角分线轴对称图形等腰三角形等边三角形一、轴对称与轴对称图形：1、轴对称：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，两个图形中的对应点叫做对称点，对应线段叫做对称线段。

2、轴对称图形：如果一个图形沿着一条直线折叠，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线就是它的对称轴。

【注意】对称轴是直线而不是线段3、轴对称的性质：（1）关于某条直线对称的两个图形是全等形；（2）如果两个图形关于某条直线对称，那么对称轴是对应点连线的垂直平分线；（3）两个图形关于某条直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上； （4）如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。

二、线段垂直平分线：1、定义：垂直平分一条线段的直线是这条线的垂直平分线。

2、性质：线段垂直平分线上的点到这条线段两个端点的距离相等；3、判定：到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．中考大纲知识精讲知识网络图【注意】1、据线段垂直平分线的这一特性可以推出：三角形三边的垂直平分线交于一点，并且这一点到三个顶点的距离相等。

2、垂直平分线中线段的中点的特殊性，常需要分类讨论．三、角的平分线：1、定义：把一个角分成两个相等的角的射线叫做角的平分线.2、性质：在角的平分线上的点到这个角的两边的距离相等.3、判定：到一个角的两边距离相等的点，在这个角的平分线上.【注意】根据角平分线的性质，三角形的三个内角的平分线交于一点，并且这一点到三条边的距离相等.3、角分线常见辅助线（1）往角两边作垂线用角平分线上的点往角两边作垂线，这是常用的辅助线，可以利用边角边构造全等（2）往角两边截取相等的线段在角两边截取相等的线段，这也是角平分线常用的辅助线，常用于解决线段和差问题（3）：过角平分线上的点作垂线过角平分线上的点作垂线，常用于构造三线合一，构造等腰三角形（4）：过角平分线上的点作角一边的平行线可以构造等腰三角形，可以记作口诀：“角平分线+平行线，等角三角形现。

中考数学复习----《图形的对称变换》知识点总结与专项练习题（含答案解析）知识点总结1. 轴对称与轴对称图形的概念：①轴对称的概念：把一个图形沿某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，也称轴对称；这条直线叫做对称轴。

②轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也可以说这个图形关于这条直线（成轴）对称。

2. 轴对称的性质：①成轴对称的两个图形全等。

即有对应边相等，对应角相等。

②对称轴是任意一组对应点连线的垂直平分线。

3. 关于坐标轴对称的点的坐标：①关于x 轴对称的点的坐标：横坐标不变，纵坐标互为相反数。

即()b a ，关于x 轴对称的点的坐标为()b a −，。

②关于y 轴对称的点的坐标：纵坐标不变，横坐标互为相反数。

即()b a ，关于y 轴对称的点的坐标为()b a ，−。

③关于原点对称的点的坐标：横纵坐标均互为相反数。

即()b a ，关于原点对称的点的坐标为()b a −−，。

4. 关于直线对称的点的坐标：①关于直线m x =对称，()b a P ，⇒()b a m P ，−2②关于直线n y =对称，()b a P ，⇒()b n a P −22 ，练习题1、（2022•六盘水）下列汉字中，能看成轴对称图形的是（ ）A ．坡B ．上C ．草D ．原【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．【解答】解：A，B，D选项中的汉字都不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；C选项中的汉字能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；故选：C．2、（2022•福建）美术老师布置同学们设计窗花，下列作品为轴对称图形的是（）A．B．C．D．【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．【解答】解：选项B、C、D不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形，选项A能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，故选：A．3、（2022•贵港）若点A（a，﹣1）与点B（2，b）关于y轴对称，则a﹣b的值是（）A．﹣1B．﹣3C．1D．2【分析】根据两点关于y轴对称的点的坐标的特点列出有关a、b的方程求解即可求得a ﹣b的值．【解答】解：∵点A（a，﹣1）与点B（2，b）关于y轴对称，∴a＝﹣2，b＝﹣1，∴a﹣b＝﹣2﹣（﹣1）＝﹣1，故选：A．4、（2022•常州）在平面直角坐标系xOy中，点A与点A1关于x轴对称，点A与点A2关于y轴对称．已知点A1（1，2），则点A2的坐标是（）A．（﹣2，1）B．（﹣2，﹣1）C．（﹣1，2）D．（﹣1，﹣2）【分析】关于x轴的对称点的坐标特点：横坐标不变，纵坐标互为相反数．关于y轴的对称点的坐标特点：横坐标互为相反数，纵坐标不变．【解答】解：∵点A与点A1关于x轴对称，已知点A1（1，2），∴点A的坐标为（1，﹣2），∵点A与点A2关于y轴对称，∴点A2的坐标为（﹣1，﹣2），故选：D．5、（2022•新疆）在平面直角坐标系中，点A（2，1）与点B关于x轴对称，则点B的坐标是（）A．（2，﹣1）B．（﹣2，1）C．（﹣2，﹣1）D．（2，1）【分析】直接利用关于x轴对称点的性质，横坐标不变，纵坐标改变符号，进而得出答案．【解答】解：∵点A（2，1）与点B关于x轴对称，∴点B的坐标是：（2，﹣1）．故选：A．6、（2022•六盘水）如图，将一张长方形纸对折，再对折，然后沿图中虚线剪下，剪下的图形展开后可得到（）A．三角形B．梯形C．正方形D．五边形【分析】动手操作可得结论．【解答】解：将一张长方形纸对折，再对折，然后沿图中虚线剪下，剪下的图形展开后可得到：正方形．故选：C．。

中考数学复习《对称、平移与旋转》专项测试卷(含参考答案)学校:___________班级：___________姓名：___________考号：___________知识点一、轴对称1、下列图案中，是轴对称图形的是（）A．B．C．D．2、在美术字中，有些汉字可以看成是轴对称图形．下列汉字中，是轴对称图形的是（）A．B．C．D．3、如图，△ABC与△A′B′C′关于直线l对称，∠A＝50°，∠C′＝30°，则∠B的度数为（）A．90°B．100°C．70°D．80°4、如图，∠AOB内一点P，P1，P2分别是P关于OA、OB的对称点，P1P2交OA于点M，交OB于点N．若△PMN的周长是5cm，则P1P2的长为（）A．3cm B．4cm C．5cm D．6cm5、如图，在Rt△ACB中，∠BAC＝90°，AD⊥BC，垂足为D，△ABD与△ADB′关于直线AD对称，点B的对称点是点B′，若∠B′AC＝14°，则∠B的度数为（）A．38°B．48°C．50°D．52°知识点二、中心对称1、搭载神舟十六号载人飞船的长征二号F遥十六运载火箭于2023年5月30日成功发射升空，景海鹏、朱杨柱、桂海潮3名航天员开启“太空出差”之旅，展现了中国航天科技的新高度．下列图标中，其文字上方的图案是中心对称图形的是（）A．B．C．D．2、将四个数字看作一个图形，则下列四个图形中，是中心对称图形的是（）A．B．C．D．3、在平面直角坐标系中，已知点A（﹣4，3）与点B关于原点对称，则点B的坐标为（）A．（﹣4，﹣3）B．（4，3）C．（4，﹣3）D．（﹣4，3）4、在平面直角坐标系中，点（a+2，2）关于原点的对称点为（4，﹣b），则ab的值为（）A．﹣4B．4C．12D．﹣125、在平面直角坐标系中，若点P（m，m﹣n）与点Q（﹣2，3）关于原点对称，则点M（m，n）在（）A．第一象限B．第二象限C．第三象限D．第四象限6、如图，△ABC与△A′B′C′关于点O成中心对称，则下列结论不成立的是（）A．点A与点A′是对称点B．BO＝B′OC．AB∥A′B′D．∠ACB＝∠C′A′B′知识点三、平移1、如图，将△ABC沿BC向右平移得到△DEF，若BC＝5，BE＝2，则CF的长是（）A．2B．2.5C．3D．52、如图，已知点A（1，0），B（4，m），若将线段AB平移至CD，其中点C（﹣2，1），D（a，n），则m﹣n的值为（）A．﹣3B．﹣1C．1D．33、在直角坐标系中，把点A（m，2）先向右平移1个单位，再向上平移3个单位得到点B．若点B的横坐标和纵坐标相等，则m＝（）A．2B．3C．4D．54、如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB＝10，DO＝4，平移距离为6，则阴影部分面积为（）A．48B．96C．84D．425、如图，将△ABE向右平移2cm得到△DCF，如果△ABE的周长是16cm，那么四边形ABFD的周长是（）A．16cm B．18cm C．20cm D．21cm6、如图，把△ABC沿着BC的方向平移到△DEF的位置，它们重叠部分的面积是△ABC面积的一半，若BC＝，则△ABC移动的距离是（）A．B．C．D．﹣7、如图，将△ABC沿BC边上的中线AD平移到△A′B′C′的位置．已知△ABC的面积为16，阴影部分三角形的面积9．若AA′＝1，则A′D等于（）A．2B．3C．4D．知识点四、旋转1、如图，△AOB绕点O逆时针旋转65°得到△COD，若∠COD＝30°，则∠BOC的度数是（）A．30°B．35°C．40°D．45°2、如图，△ABC中，∠ACB＝90°，∠ABC＝40°．将△ABC绕点B逆时针旋转得到△A′BC′，使点C的对应点C′恰好落在边AB上，则∠CAA′的度数是（）A．50°B．70°C．110°D．120°3、如图，在△ABC中，∠CAB＝65°，将△ABC在平面内绕点A旋转到△AB'C'的位置，使CC'∥AB，则旋转角的度数为（）A．35°B．40°C．50°D．65°4、如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，AC＝3，将△ABC绕点C按逆时针方向旋转得到△A′B′C，此时点A′恰好在AB边上，连接BB′，则BB′的长为（）A．6B．C．D．35、如图，在△ABC中，∠BAC＝108°，将△ABC绕点A按逆时针方向旋转得到△AB′C′．若点B′恰好落在BC边上，且AB＝CB′，则∠C′的度数为（）A．18°B．20°C．24°D．28°6、如图，矩形ABCD绕B点旋转，使C点落到AD上的E处，AB＝AE，连接AF，AG．（1）求证：AF＝AG；（2）求∠GAF的度数．7、已知，点P是等边三角形△ABC中一点，线段AP绕点A逆时针旋转60°到AQ，连接PQ、QC．（1）求证：△BAP≌△CAQ．（2）若P A＝3，PB＝4，∠APB＝150°，求PC的长度．参考答案知识点一、轴对称1-5 ACBCD知识点二、中心对称1-6 CDCDAD知识点三、平移1-7 ABCAC DB知识点四、旋转1-5 BDCCC6、（1）证明：由旋转性质，得∠GBE＝∠FEB＝90°，BG＝CD＝EF∵AB＝AE∴∠ABE＝∠AEB∴∠ABG＝∠AEF在△ABG和△AEF中，AB＝AE，∠ABG＝∠AEF，BG＝EF∴△ABG≌△AEF∴AG＝AF（2）解：∵AB＝AE，∠BAE＝90°∴∠ABE＝∠AEB＝45°∴∠ABG＝90°﹣45°＝45°由旋转性质，得AB＝BG∴∠BAG＝∠AGB＝67.5°∵△ABG≌△AEF∴∠EAF＝∠BAG＝67.5°∴∠GAF＝360°﹣90°﹣67.5°﹣67.5°＝135°7、（1）证明：由旋转性质，得AP＝AQ，∠P AQ＝60°∴∠P AC+∠CAQ＝60°∵△ABC是等边三角形∴∠P AC+∠BAP＝60°，AB＝AC∴∠BAP＝∠CAQ在△BAP和△CAQ中，AP＝AQ，∠BAP＝∠CAQ，AB＝AC ∴△BAP≌△CAQ（2）解：∵AP＝AQ＝3，∠P AQ＝60°∴AP＝PQ＝3，∠AQP＝60°∵∠APB＝150°∴∠PQC＝∠APB﹣∠AQP＝90°∵PB＝QC＝4∴PC＝＝5。

2020中考数学专题练习：图形的轴对称、平移与旋转（含答案）A级基础题1．下列图形中，是轴对称图形的是()2．在平面直角坐标系中，点P(－1,2)关于x轴的对称点的坐标为()A．(－1，－2) B．(1，－2)C．(2，－1) D．(－2,1)3．如图X6－1－1，将周长为8的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为()图X6－1－1A．6B．8C．10D．124．把一张正方形纸片按如图X6－1－2(1)、(2)对折两次后，再按如图X6－1－2(3)挖去一个三角形小孔，则展开后的图形是()图X6－1－25．下列图形：①平行四边形；②菱形；③圆；④梯形；⑤等腰三角形；⑥直角三角形；⑦国旗上的五角星．这些图形中既是轴对称图形又是中心对称图形的有()A．1种B．2种C．3种D．4种6．如图X6－1－3，矩形ABCD中，点E在边AB上，将矩形ABCD沿直线DE折叠，点A恰好落在边BC的点F处．若AE＝5，BF＝3，则CD的长是()A．7 B．8 C．9 D．10图X6－1－3图X6－1－4图X6－1－57．在平面直角坐标系中，一青蛙从点A(－1,0)处向右跳2个单位长度，再向上跳2个单位长度到点A′处，则点A′的坐标为__________．8．如图X6－1－4，点D是等边△ABC内的一点，如果△ABD绕点A逆时针旋转后能与△ACE重合，那么旋转了________度．9．分别以正方形的各边为直径向其内部作半圆得到的图形如图X6－1－5.将该图形绕其中心旋转一个合适的角度后会与原图形重合，则这个旋转角的最小度数是__________ 度．图X6－1－610．如图X6－1－6，在Rt△ABC中，∠B＝90°，沿AD折叠，使点B落在斜边AC上，若AB＝3，BC ＝4，则BD＝__________.11．如图X6－1－7，梯形ABCD是直角梯形．(1)直接写出点A，B，C，D的坐标；(2)画出直角梯形ABCD关于y轴的对称图形，使它与梯形ABCD构成一个等腰梯形；(3)将(2)中的等腰梯形向上平移四个单位长度，画出平移后的图形(不要求写作法)．图X6－1－712．如图X6－1－8，将一个钝角△ABC(其中∠ABC＝120°)绕点B顺时针旋转得△A1BC1，使得点C落在AB的延长线上的点C1处，连接AA1.(1)写出旋转角的度数；(2)求证：∠A1AC＝∠C1.图X6－1－8B级中等题图X6－1－913．如图X6－1－9，在Rt△ABC中，∠C＝90°，AC＝4，将△ABC沿CB向右平移得到△DEF，若平移距离为2，则四边形ABED的面积等于________．14．在平面直角坐标系中，O为坐标原点，点A的坐标为(3，1)，将OA绕原点按逆时针方向旋转30°得OB，则点B的坐标为()A．(1，3) B．(－1，3)C．(0,2) D．(2,0)15．如图X6－1－10，在Rt△ABC中，∠ABC＝90°，点D在BC的延长线上，且BD＝AB，过点B作BE ⊥AC，与BD的垂线DE交于点E.(1)求证：△ABC≌△BDE；(2)△BDE可由△ABC旋转得到，利用尺规作出旋转中心O(保留作图痕迹，不写作法)．图X6－1－10C级拔尖题16．如图X6－1－11，在平面直角坐标系中，有一Rt△ABC，且A(－1,3)，B(－3，－1)，C(－3,3)，已知△A1AC1是由△ABC旋转得到的．(1)请写出旋转中心的坐标是________，旋转角是________度；(2)以(1)中的旋转中心为中心，分别画出△A 1AC 1顺时针旋转90°、180°的三角形；(3)设Rt △ABC 两直角边BC ＝a ，AC ＝b ，斜边AB ＝c ，利用变换前后所形成的图X6－案证明勾股定理．图X6－1－11选做题17．如图X6－1－12，O 为正方形ABCD 的中心，分别延长OA ，OD 到点F ，E ，使OF ＝2OA ，OE ＝2OD ，连接EF .将△EOF 绕点O 逆时针旋转α角得到△E 1OF 1(如图X6－1－13)．(1)探究AE 1与BF 1的数量关系，并给予证明； (2)当α＝30°时，求证：△AOE 1为直角三角形．图X6－1－12图X6－1－13参考答案1．B 2.A 3.C 4.C 5.B 6.C 7.(1,2) 8.609．90 10.3211．解：(1)如图D66，根据A ，B ，C ，D 的位置得出点A ，B ，C ，D 的坐标分别为(－2，－1)，(－4，－4)，(0，－4)，(0，－1)．(2)根据A，B两点关于y轴对称点分别为A′(2，－1)，(4，－4)，连接各点，即可得出图象，如图D66.(3)将对应点分别向上移动4个单位，即可得出图象，如图D.图D6612．(1)解：∵∠ABC＝120°，∴∠CBC1＝180°－∠ABC＝180°－120°＝60°，∴旋转角为60°.(2)证明：由题意可知，△ABC≌△A1BC1，∴A1B＝AB，∠C＝∠C1，由(1)，知∠ABA1＝60°，∴△A1AB是等边三角形．∴∠BAA1＝60°.∴∠BAA1＝∠CBC1.∴AA1∥BC，∴∠A1AC＝∠C.∴∠A1AC＝∠C1.13．814.A15．(1)证明：在Rt△ABC中，∵∠ABC＝90°，∴∠ABE＋∠DBE＝90°.∵BE⊥AC，∴∠ABE＋∠A＝90°.∴∠A＝∠DBE.∵DE是BD的垂线，∴∠D＝90°.在△ABC和△BDE中，∵∠A＝∠DBE，AB＝DB，∠ABC＝∠D，∴△ABC≌△BDE(ASA)．(2)作法一：如图D67(1)，点O就是所求作的旋转中心．作法二：如图D67(2)，点O就是所求作的旋转中心．图D6716．解：(1)旋转中心的坐标是O(0,0)，旋转角是90度．(2)画出的图形如图D68：图D68(3)由旋转的过程可知，四边形CC 1C 2C 3和四边形AA 1A 2B 是正方形． ∵S 正方形CC 1C 2C 3＝S 正方形AA 1A 2B ＋4S △ABC ，∴(a ＋b )2＝c 2＋4×12ab ，即a 2＋2ab ＋b 2＝c 2＋2ab ，∴a 2＋b 2＝c 2.17．(1)解：AE 1＝BF 1.证明：∵O 为正方形ABCD 的中心，∴OA ＝OD . ∵OF ＝2OA ，OE ＝2OD ，∴OE ＝OF .∵将△EOF 绕点O 逆时针旋转α角得到△E 1OF 1， ∴OE 1＝OF 1.∵∠F 1OB ＝∠E 1OA ，OA ＝OB ， ∴△E 1AO ≌△F 1BO . ∴AE 1＝BF 1.图D69(2)证明：如图D69，取OE 1中点G ，连接AG ， ∵∠AOD ＝90°，α＝30°. ∴∠E 1OA ＝90°－α＝60°. ∵OE 1＝2OA ， ∴OA ＝OG .∴∠E 1OA ＝∠AGO ＝∠OAG ＝60°. ∴AG ＝GE 1.∴∠GAE 1＝∠GE 1A ＝30°. ∴∠E 1AO ＝90°.∴△AOE 1为直角三角形．。

初三数学图形的对称平移与旋转试题答案及解析1.如图，在Rt△ABC中，∠BAC=90°．如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置，点B1恰好落在边BC的中点处．那么旋转的角度等于（）A．55°B．60°C．65°D．80°【答案】B【解析】∵在Rt△ABC中，∠BAC=90°，将该三角形绕点A按顺时针方向旋转到△AB1C1的位置，点B1恰好落在边BC的中点处，∴AB1=BC，BB1=B1C，AB=AB1，∴BB1=AB=AB1，∴△ABB1是等边三角形，∴∠BAB1=60°，∴旋转的角度等于60°．故选：B．【考点】旋转的性质2.如图1，小红将一张直角梯形纸片沿虚线剪开，得到矩形和三角形两张纸片，测得AB=15，AD=12．在进行如下操作时遇到了下面的几个问题，请你帮助解决．（1）将△EFG的顶点G移到矩形的顶点B处，再将三角形绕点B顺时针旋转使E点落在CD边上，此时，EF恰好经过点A（如图2）求FB的长度（2）在（1）的条件下，小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4，请问哪种包裹纸片的方法使得未包裹住的面积大？（纸片厚度忽略不计）请你通过计算说服小红。

【答案】(1)30;(2) 二种包裹纸片的方法使得未包裹住的面积相等．【解析】（1）利用矩形的性质以及得出△ADE ∽△FBE ，求出即可；(2)根据Rt △F ，HN ～Rt △F ，EG ，得到HN=3，从而S △AMH =144；由Rt △GBE ～Rt △C ，B ,G ，得到GB ,=24，从而S △B ,C ,G =144，进行比较即可．⑴BE=AD=15，在RtBCE 中，CE 2="B" E 2-BC 2=152-122，求得CE=9，DE=6， 证Rt △ADE ～Rt △FBE, 求得BF="30"⑵①如图1，将矩形ABCD 和Rt △FBE 以CD 为轴翻折，则△AMH 即为未包裹住的面积，由Rt △F ，HN ～Rt △F ，EG ，得到HN=3， 从而S △AMH =144②如图2，将矩形ABCD 和Rt △ECF 以AD 为轴翻折,由Rt △GBE ～Rt △C ，B ,G ，得到GB ,=24，从而S △B ,C ,G =144,∴未包裹的面积为144． ∴按照二种包裹的方法未包裹的面积相等。