2017届高三数学一轮复习-防错纠错1 集合与简易逻辑 Word版含答案答案

高考数学一轮总复习：第一章集合与简易逻辑第1课时集合1．下列各组集合中表示同一集合的是( )A．M＝{(3，2)}，N＝{(2，3)}B．M＝{2，3}，N＝{3，2}C．M＝{(x，y)|x＋y＝1}，N＝{y|x＋y＝1}D．M＝{2，3}，N＝{(2，3)}答案 B2．若A＝{0，1，2，3}，B＝{x|x＝3a，a∈A}，则A∩B＝( ) A．{1，2} B．{0，1}C．{0，3} D．{3}答案 C解析B＝{x|x＝3a，a∈A}＝{0，3，6，9}，所以A∩B＝{0，3}．3．设集合M＝{x|x2＝x}，N＝{x|lgx≤0}，则M∪N＝( ) A．[0，1] B．(0，1]C．[0，1) D．(－∞，1]答案 A解析集合M＝{0，1}，集合N＝{x|0<x≤1}，M∪N＝{x|0≤x≤1}，所以M∪N＝[0，1]．4．若A＝{x|x2－2x<0}，B＝{x|1x≤1}，则A∩B＝( )A．(0，1) B．(0，2) C．(1，2) D．[1，2) 答案 D解析因为A＝{x|x2－2x<0}＝{x|0<x<2}，B＝{x|1x≤1}＝{x|x≥1或x<0}，所以A∩B＝{x|1≤x<2}．5．已知m∈A，n∈B，且集合A＝{x|x＝2a，a∈Z}，B＝{x|x＝2b＋1，b∈Z}，C＝{x|x＝4c＋1，c∈Z}，则有( )A．m＋n∈A B．m＋n∈BC．m＋n∈C D．m＋n不属于A，B，C中任意一个集合答案 B解析∵m∈A，∴设m＝2a1，a1∈Z，又n∈B，∴设n＝2b1＋1，b1∈Z，∴m＋n＝2(a1＋b1)＋1，而a1＋b1∈Z，∴m＋n∈B，故选B.6．已知集合A＝{x∈N|πx<16}，B＝{x|x2－5x＋4<0}，则A∩(∁R B)的真子集的个数为( )A．1 B．3C．4 D．7答案 B解析因为A＝{x∈N|πx<16}＝{0，1，2}，B＝{x|x2－5x＋4<0}＝{x|1<x<4}，故∁R B＝{x|x≤1或x≥4}，故A∩(∁R B)＝{0，1}，故A∩(∁R B)的真子集的个数为22－1＝3，故选B.7．设集合A＝{x||x－1|<2}，B＝{y|y＝2x，x∈[0，2]}，则A∩B＝( ) A．[0，2] B．(1，3)C．[1，3) D．(1，4)答案 C解析|x－1|<2⇔－2<x－1<2，故－1<x<3，即集合A＝(－1，3)．根据指数函数的性质，可得集合B＝[1，4]．所以A∩B＝[1，3)．8．已知实数集R，集合A＝{x|log2x<1}，B＝{x∈Z|x2＋4≤5x}，则(∁R A)∩B ＝( )A．[2，4] B．{2，3，4}C．{1，2，3，4} D．[1，4]答案 B解析由log2x<1，解得0<x<2，故A＝(0，2)，故∁R A＝(－∞，0]∪[2，＋∞)，由x2＋4≤5x，即x2－5x＋4≤0，解得1≤x≤4，又x∈Z，所以B＝{1，2，3，4}．故(∁R A)∩B＝{2，3，4}．故选B.9．若全集U＝R，集合A＝{x|1<2x<4}，B＝{x|x－1≥0}，则A∩(∁UB)＝( )A．{x|1<x<2} B．{x|0<x≤1}C．{x|0<x<1} D．{x|1≤x<2}答案 C解析由题意知，A＝{x|0<x<2}，B＝{x|x≥1}，∁UB＝{x|x<1}，所以A∩(∁UB)＝{x|0<x<1}．10．已知全集U为R，集合A＝{x|x2<16}，B＝{x|y＝log3(x－4)}，则下列关系正确的是( )A．A∪B＝R B．A∪(∁UB)＝RC．(∁U A)∪B＝R D．A∩(∁UB)＝A答案 D解析因为A＝{x|－4<x<4}，B＝{x|x>4}，所以∁UB＝{x|x≤4}，所以A∩(∁UB)＝A，故选D.11．已知集合A＝{x|x>2}，B＝{x|x<2m，m∈R}且A⊆∁R B，那么m的值可以是( )A．1 B．2C．3 D．4答案 A解析由B＝{x|x<2m，m∈R}，得∁R B＝{x|x≥2m，m∈R}．因为A⊆∁R B，所以2m≤2，m≤1，故选A.12．已知集合A＝{x|1<x<k}，集合B＝{y|y＝2x－5，x∈A}，若A∩B＝{x|1<x<2}，则实数k的值为( )A．5 B．4.5C．2 D．3.5答案 D解析B＝(－3，2k－5)，由A∩B＝{x|1<x<2}，知k＝2或2k－5＝2，因为k＝2时，2k－5＝－1，A∩B＝∅，不合题意，所以k＝3.5，故选D.13．已知函数f(x)的图像如图所示，设集合A＝{x|f(x)>0}，B＝{x|x2<4}，则A∩B＝( )A．(－2，－1)∪(0，2) B．(－1，1)C ．(－2，－1)∪(1，2)D ．(－∞，3)答案 C解析 由题意可得A ＝(－∞，－1)∪(1，3)，B ＝(－2，2)，所以A∩B＝(－2，－1)∪(1，2)．14． 集合A ＝{0，|x|}，B ＝{1，0，－1}，若A ⊆B ，则A∩B＝________，A ∪B ＝________，∁B A ＝________．答案 {0，1} {1，0，－1} {－1}解析 因为A ⊆B ，所以|x|∈B，又|x|≥0，结合集合中元素的互异性，知|x|＝1，因此A ＝{0，1}，则A∩B＝{0，1}，A ∪B ＝{1，0，－1}，∁B A ＝{－1}．15．设全集U ＝A∪B＝{x∈N *|lgx<1}，若A∩(∁U B)＝{m|m ＝2n ＋1，n ＝0，1，2，3，4}，则集合B ＝________．答案 {2，4，6，8}解析 U ＝{1，2，3，4，5，6，7，8，9}，A ∩(∁U B)＝{1，3，5，7，9}，∴B ＝{2，4，6，8}．16． 已知集合A ＝{x|log 2x<1}，B ＝{x|0<x<c}，(c>0)．若A∪B＝B ，则c 的取值范围是________．答案 [2，＋∞)解析 A ＝{x|0<x<2}，由数轴分析可得c≥2.17．已知集合P ＝{x|a ＋1≤x≤2a＋1}，Q ＝{x|x 2－3x≤10}． (1)若a ＝3，求(∁R P )∩Q；(2)若P∪Q＝Q ，求实数a 的取值范围． 答案 (1){x|－2≤x<4} (2)(－∞，2]解析 (1)因为a ＝3，所以P ＝{x|4≤x≤7}，∁R P ＝{x|x<4或x>7}．又Q ＝{x|x 2－3x －10≤0}＝{x|－2≤x≤5}，所以(∁R P )∩Q＝{x|x<4或x>7}∩{x|－2≤x≤5}＝{x|－2≤x<4}．(2)由P∪Q＝Q ，得P ⊆Q.当P≠∅时，有⎩⎨⎧a ＋1≥－2，2a ＋1≤5，2a ＋1≥a＋1，解得0≤a≤2；当P ＝∅，即2a ＋1<a ＋1时，有P ⊆Q ，得a<0.综上，实数a 的取值范围是(－∞，2]．18．已知集合A ＝{x|1<x<3}，集合B ＝{x|2m<x<1－m}． (1)若A ⊆B ，求实数m 的取值范围；(2)若A∩B＝(1，2)，求实数m 的取值范围； (3)若A∩B＝∅，求实数m 的取值范围．答案 (1)(－∞，－2] (2)m ＝－1 (3)[0，＋∞)解析(1)由A ⊆B ，得⎩⎨⎧1－m>2m ，2m ≤1，1－m≥3，得m≤－2，即实数m 的取值范围为(－∞，－2]． (2)由已知，得⎩⎨⎧2m≤1，1－m ＝2⇒⎩⎨⎧m ≤12，m ＝－1，∴m ＝－1.(3)由A∩B＝∅，得①若2m≥1－m ，即m≥13时，B ＝∅，符合题意；②若2m<1－m ，即m<13时，需⎩⎨⎧m<13，1－m≤1或⎩⎨⎧m<13，2m ≥3，得0≤m<13或∅，即0≤m<13.综上知m≥0，即实数m 的取值范围为[0，＋∞)．第2课时 命题及其关系、充分条件与必要条件1． 命题“若x 2<1，则－1<x<1”的逆否命题是( ) A ．若x 2≥1，则x≥1或x≤－1 B ．若－1<x<1，则x 2<1 C ．若x>1或x<－1，则x 2>1 D ．若x≥1或x≤－1，则x 2≥1 答案 D解析原命题的逆否命题是把条件和结论都否定后，再交换位置，注意“－1<x<1”的否定是“x≥1或x≤－1”．2．命题“若m>－1，则m>－4”以及它的逆命题、否命题、逆否命题中，假命题的个数为( )A．1 B．2C．3 D．4答案 B解析原命题为真命题，从而其逆否命题也为真命题；逆命题“若m>－4，则m>－1”为假命题，故否命题也为假命题，故选B.3．命题“若x2＋y2＝0，则x＝y＝0”的否命题是( )A．若x2＋y2＝0，则x，y中至少有一个不为0B．若x2＋y2≠0，则x，y中至少有一个不为0C．若x2＋y2≠0，则x，y都不为0D．若x2＋y2＝0，则x，y都不为0答案 B解析否命题既否定条件又否定结论．4．下列命题中为真命题的是( )A．命题“若x>y，则x>|y|”的逆命题B．命题“若x2≤1，则x≤1”的否命题C．命题“若x＝1，则x2－x＝0”的否命题D．命题“若a>b，则1a<1b”的逆否命题答案 A解析A中原命题的逆命题是“若x>|y|，则x>y”，由x>|y|≥y可知其是真命题；B中原命题的否命题是“若x2>1，则x>1”，是假命题，因为x2>1⇔x>1或x<－1；C中原命题的否命题是“若x≠1，则x2－x≠0”，是假命题；D中原命题的逆命题是“若1a≥1b，则a≤b”是假命题，举例：a＝1，b＝－1，故选A.5．若命题p的否命题是命题q的逆否命题，则命题p是命题q的( ) A．逆命题B．否命题C．逆否命题D．p与q是同一命题答案 A解析设p：若A，则B，则p的否命题为若綈A，则綈B，从而命题q为若B，则A，则命题p是命题q的逆命题，故选A.6．设有下面四个命题：p 1：若复数z满足1z∈R，则z∈R；p2：若复数z满足z2∈R，则z∈R；p 3：若复数z1，z2满足z1z2∈R，则z1＝z2；p 4：若复数z∈R，则z－∈R.其中的真命题为( )A．p1，p3B．p1，p4C．p2，p3D．p2，p4答案 B解析对于p1，由1z∈R，即z－z·z－∈R得z－|z|2∈R，∴z－∈R，∴z∈R.故p1为真命题．对于p2，显然i2＝－1，但i∉R.故p2为假命题．对于p3，若z1＝1，z2＝2，则z1z2＝2，满足z1z2∈R，而它们的实部不相等，不是共轭复数．故p3为假命题．对于p4，z∈R，则z－∈R.故p4为真命题，故选B.7．祖暅原理：“幂势既同，则积不容异”．它是中国古代一个涉及几何体体积的问题，意思是两个同高的几何体，如在等高处截面的面积恒相等，则体积相等．设A，B为两个同高的几何体，p：A，B的体积不相等，q：A，B在等高处的截面积不恒相等，根据祖暅原理可知，p是q的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案 A解析p⇒q，而q p，∴选A.8．“α＝π6＋2kπ(k∈Z )”是“cos2α＝12”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件答案 A解析 由α＝π6＋2kπ(k∈Z )，知2α＝π3＋4kπ(k∈Z )，则cos2α＝cosπ3＝12成立， 当cos2α＝12时，2α＝2kπ±π3，即α＝kπ±π6(k∈Z )，故选A.9． “1x >1”是“e x －1<1”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案 A解析 ∵1x >1，∴x ∈(0，1)．∵e x －1<1，∴x<1.∴“1x>1”是“e x －1<1”的充分不必要条件．10． 设a ，b ∈R ，则“a>b”是“a|a|>b|b|”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件答案 C解析 构造函数f(x)＝x|x|，则f(x)在定义域R 上为奇函数．因为f(x)＝⎩⎨⎧x 2，x ≥0，－x 2，x ＜0，所以函数f(x)在R 上单调递增，所以a>b ⇔f(a)>f(b)⇔a|a|>b|b|.选C.11． “(m－1)(a －1)>0”是“log a m>0”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件答案 B解析 (m －1)(a －1)>0等价于⎩⎨⎧m>1，a>1或⎩⎨⎧m<1，a<1，而log a m>0等价于⎩⎨⎧m>1，a>1或⎩⎨⎧0<m<1，0<a<1，所以条件具有必要性，但不具有充分性，比如m ＝0，a ＝0时，不能得出log a m>0，故选B.12． 命题“对任意x∈[1，2)，x 2－a≤0”为真命题的一个充分不必要条件可以是( )A ．a ≥4B ．a>4C ．a ≥1D ．a>1答案 B解析 由题意知a≥x 2，对x∈[1，2)恒成立，当x∈[1，2)时，1≤x 2<4，则a≥4.从而a>4是命题为真的一个充分不必要条件．13．若不等式13<x<12的必要不充分条件是|x －m|<1，则实数m 的取值范围是( )A ．[－43，12]B ．[－12，43]C ．(－∞，12)D ．(43，＋∞)答案 B解析 由|x －m|<1，解得m －1<x<m ＋1.因为不等式13<x<12的必要不充分条件是|x －m|<1，所以⎩⎪⎨⎪⎧m －1≤13，12≤m ＋1，且等号不能同时取得，解得－12≤m ≤43，故选B.14． 若“x>1”是“不等式2x >a －x 成立”的必要而不充分条件，则实数a 的取值范围是( )A ．a>3B ．a<3C ．a>4D ．a<4 答案 A解析 若2x >a －x ，即2x ＋x>a.设f(x)＝2x ＋x ，则函数f(x)为增函数．由题意知“2x ＋x>a 成立，即f(x)>a 成立”能得到“x>1”，反之不成立．因为当x>1时，f(x)>3，∴a>3.15．(1)“x>y>0”是“1x <1y ”的________条件．(2)“tanθ≠1”是“θ≠π4”的________条件．答案 (1)充分不必要 (2)充分不必要 解析 (1)1x <1y ⇒xy ·(y －x)<0，即x>y>0或y<x<0或x<0<y. (2)题目即判断θ＝π4是tanθ＝1的什么条件，显然是充分不必要条件． 16． 下列不等式：①x<1；②0<x<1；③－1<x<0；④－1<x<1.其中可以作为“x 2<1”的一个充分条件的所有序号为________． 答案 ②③④17．设命题p ：2x －1x －1<0，命题q ：x 2－(2a ＋1)x ＋a(a ＋1)≤0，若p 是q 的充分不必要条件，求实数a 的取值范围．答案 [0，12]解析 2x －1x －1<0⇒(2x －1)(x －1)<0⇒12<x<1，x 2－(2a ＋1)x ＋a(a ＋1)≤0⇒a ≤x ≤a ＋1， 由题意得(12，1)[a ，a ＋1]，故⎩⎨⎧a ≤12，a ＋1≥1，解得0≤a≤12.第3课时 逻辑联结词与量词1．下列命题中的假命题是( )A．∀x∈R，e x－1>0 B．∀x∈N*，(x－1)2>0 C．∃x∈R，lnx<1 D．∃x∈R，tanx＝2答案 B解析因为当x＝1时，(x－1)2＝0，所以B为假命题，故选B.2．命题“∃x0∈∁RQ，x3∈Q”的否定是( )A．∃x0∉∁RQ，x3∈Q B．∃x∈∁RQ，x3∈QC．∀x∉∁R Q，x3∈Q D．∀x∈∁RQ，x3∉Q答案 D解析该特称命题的否定为“∀x∈∁RQ，x3∉Q”．3．命题“∀x∈R，f(x)·g(x)≠0”的否定是( )A．∀x∈R，f(x)＝0且g(x)＝0 B．∀x∈R，f(x)＝0或g(x)＝0C．∃x0∈R，f(x)＝0且g(x)＝0 D．∃x∈R，f(x)＝0或g(x)＝0答案 D解析根据全称命题与特称命题的互为否定的关系可得：命题“∀x∈R，f(x)g(x)≠0”的否定是“∃x0∈R，f(x)＝0或g(x)＝0”．故选D.4．若命题p：x∈A∩B，则綈p：( )A．x∈A且x∉B B．x∉A或x∉BC．x∉A且x∉B D．x∈A∪B答案 B5．下列命题的否定是真命题的是( )A．有些实数的绝对值是正数B．所有平行四边形都不是菱形C．任意两个等边三角形都是相似的D．3是方程x2－9＝0的一个根答案 B6．已知命题p，q，“綈p为真”是“p∧q为假”的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案 A解析因为綈p为真，所以p为假，那么p∧q为假，所以“綈p为真”是“p∧q为假”的充分条件；反过来，若“p∧q为假”，则“p真q假”或“p假q真”或“p假q假”，所以由“p∧q为假”不能推出綈p为真．综上可知，“綈p为真”是“p∧q为假”的充分不必要条件．7．设x∈Z，集合A是奇数集，集合B是偶数集．若命题p：∀x∈A，2x∈B，则( )A．綈p：∀x∈A，2x∉B B．綈p：∀x∉A，2x∉BC．綈p：∃x∉A，2x∈B D．綈p：∃x∈A，2x∉B答案 D解析因全称命题的否定是特称命题，故命题的否定为綈p：∃x∈A，2x∉B.故选D.8．已知集合A＝{y|y＝x2＋2}，集合B＝{x|y＝lg x－3}，则下列命题中真命题的个数是( )①∃m∈A，m∉B；②∃m∈B，m∉A；③∀m∈A，m∈B；④∀m∈B，m∈A.A．4 B．3C．2 D．1答案 C解析因为A＝{y|y＝x2＋2}，所以A＝{y|y≥2}，因为B＝{x|y＝lg x－3}，所以B＝{x|x>3}，所以B是A的真子集，所以①④为真，②③为假命题，所以真命题的个数为2，故选C.9．下列4个命题中，其中的真命题是( )p 1：∃x∈(0，＋∞)，(12)x<(13)xp2：∃x∈(0，1)，log12x>log13xp 3：∀x∈(0，＋∞)，(12)x<log12xp 4：∀x∈(0，13)，(12)x<log13xA．p1，p3B．p1，p4C．p2，p3D．p2，p4答案 D解析 p 1，p 2为存在性命题，所以只要找到符合条件的x 即可．p 1可作出y ＝(12)x ，y ＝(13)x 的图像，通过观察发现找不到符合条件的x ；p 2同样作图可得∀x ∈(0，1)，log 12x>log 13x ，所以p 2正确；p 3通过作图可发现图像中有一部分(12)x <log 12x ，所以p 3错误；在p 4中，可得当x∈(0，13)时，(12)x <(12)0＝1，log 13x>log 13(13)＝1，所以(12)x<1<log 13x ，p 4正确．综上可得：p 2，p 4正确．10．已知命题p ：∃x 0∈R ，mx 02＋1≤0；命题q ：∀x ∈R ，x 2＋mx ＋1>0.若p∨q 为假命题，则实数m 的取值范围为( )A ．{m|m ≥2}B ．{m|m ≤－2}C ．{m|m ≤－2或m≥2}D ．{m|－2≤m≤2}答案 A解析 由p ：∃x ∈R ，mx 2＋1≤0，可得m<0；由q ：∀x ∈R ，x 2＋mx ＋1>0，可得Δ＝m 2－4<0，解得－2<m<2.因为p∨q 为假命题，所以p 与q 都是假命题，若p 是假命题，则有m≥0；若q 是假命题，则有m≤－2或m≥2，故实数m 的取值范围为{m|m≥2}．故选A.11． 已知命题p ：∃x ∈R ，lnx ＋x －2＝0，命题q ：∀x ∈R ，2x ≥x 2，则下列命题中为真命题的是( )A ．p ∧qB ．綈p∧qC ．p ∧(綈q)D ．綈p∧(綈q) 答案 C解析 分别判断p ，q 真假，令f(x)＝lnx ＋x －2，可得f(1)f(2)<0.由零点存在性定理可知∃x ∈(1，2)，使得f(x)＝lnx ＋x －2＝0，p 为真；通过作图可判断出当x∈(2，4)时，2x <x 2，故q 为假：结合选项可得：p∧(綈q)为真．12． 不等式组⎩⎨⎧x ＋y≥1，x －2y≤4的解集记为D ，有下面四个命题：p 1：∀(x ，y )∈D，x ＋2y≥－2； p 2：∃(x ，y)∈D，x ＋2y≥2； p 3：∀(x ，y )∈D，x ＋2y≤3；p 4：∃(x ，y )∈D，x ＋2y≤－1.其中的真命题是( )A．p2，p3B．p1，p4C．p1，p2D．p1，p3答案 C解析画出可行域如图所示中阴影部分，由图可知，当目标函数z＝x＋2y经过可行域内的点A(2，－1)时，z取得最小值0，故x＋2y≥0，因此p1，p2是真命题，选C.13．若命题p的否定是“对所有正数x，x>x＋1”，则命题p是________．答案∃x0∈(0，＋∞)，x≤x＋114．已知p：1x2－x－2>0，则綈p对应的x的集合为________．答案{x|－1≤x≤2}解析p：1x2－x－2>0⇔x>2或x<－1，∴綈p：－1≤x≤2.注：本题若利用綈p：1x2－x－2≤0求解会致误．15．已知命题“∀x∈R，sinx－a≥0”是真命题，则a的取值范围是________．答案(－∞，－1]解析由题意，对∀x∈R，a≤sinx成立．由于对∀x∈R，－1≤sinx≤1，所以a≤－1.16．若命题“∃x0∈R，x2＋(a－1)x＋1≤0”为假命题，则实数a的取值范围为________．答案(－1，3)解析由“∃x0∈R，x2＋(a－1)x＋1≤0”为假命题，得“∀x∈R，x2＋(a－1)x＋1>0”为真命题，所以Δ＝(a－1)2－4<0，解得－1<a<3，所以a的取值范围为(－1，3)．x－a≥0”，q：“存在x∈R，x2 17．已知p：“对任意的x∈[2，4]，log2＋2ax＋2－a＝0”．若p，q均为命题，而且“p且q”是真命题，求实数a的取值范围．答案a≤－2或a＝1解析p：a≤1，q：4a2－4(2－a)≥0，即a≤－2或a≥1.因为p且q是真命题，所以a≤－2或a＝1.。

．(·高考全国卷Ⅰ改编)设命题：存在∈，>，则綈为( )．存在∈，≤．对任意的∈，>．存在∈，＝．对任意的∈，≤解析：选.因为“存在∈，()”的否定是“对任意的∈，綈()”，所以命题“存在∈，>”的否定是“对任意的∈，≤”．．(·高考湖北卷改编)命题“存在∈(，＋∞)，＝－”的否定是( )．对任意的∈(，＋∞)，≠－．对任意的∉(，＋∞)，＝－．存在∈(，＋∞)，≠－．存在∉(，＋∞)，＝－解析：选.特称命题的否定为全称命题，所以存在∈(，＋∞)，＝－的否定是对任意的∈(，＋∞)，≠－，故选.．将＋＋＝(＋)改写成全称命题是( )．存在，∈，＋＋＝(＋)．存在<，>，＋＋＝(＋)．对任意的>，>，＋＋＝(＋)．对任意的，∈，＋＋＝(＋)解析：选.全称命题含有量词“任意”，故排除、，又等式＋＋＝(＋)对于全体实数都成立，故选.．下列命题中的假命题是( )．存在∈，＝．存在∈，＝．对任意的∈，>．对任意的∈，>解析：选.当＝时，＝，故命题“存在∈，＝”是真命题；当＝时，＝，故命题“存在∈，＝”是真命题；由于＝－时，<，故命题“对任意的∈，>”是假命题；根据指数函数的性质，对对任意的∈，>，故命题“对任意的∈，>”是真命题．．命题：对任意的∈(－∞，]，≤，则( )．是假命题；綈：存在∈(－∞，]，>．是假命题；綈：对任意的∈(－∞，]，≥．是真命题；綈：存在∈(－∞，]，>．是真命题；綈：对任意的∈(－∞，]，≥解析：选.因为对任意的∈(－∞，]，≤＝，所以是真命题．又因为綈：存在∈(－∞，]，>.故选.．已知命题：若＞，则－＜－；命题：若＞，则＞.在命题①且；②或；③且(綈)；④(綈)或中，真命题是( )．①③．①④．②④．②③解析：选.当＞时，－＜－，故命题为真命题，从而綈为假命题．当＞时，＞不一定成立，故命题为假命题，从而綈为真命题．由真值表知，①且为假命题；②或为真命题；③且(綈)为真命题；④(綈)或为假命题．故选.．“命题‘存在∈，＋－<’为假命题”是“－≤≤”的( )．充要条件．必要不充分条件．充分不必要条件．既不充分也不必要条件解析：选.因为“存在∈，＋－<”为假命题，所以“对任意的∈，＋－≥”为真命题．所以Δ＝＋≤，即－≤≤.所以“命题‘存在∈，＋－<’为假命题”是“－≤≤”的充要条件．．在一次跳伞训练中，甲、乙两位学员各跳一次．设命题是“甲降落在指定范围”，是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为( )．或(綈)．(綈)或(綈)．或．(綈)且(綈) 解析：选.命题“至少有一位学员没有降落在指定范围”包含以下三种情况：“甲、乙均没有降落在指定范围”“甲降落在指定范围，乙没有降落在指定范围”“乙降落在指定范围，甲没有降落在指定范围”．或者是命题“至少有一位学员没有降落在指定范围”等价于命题“甲、乙均降落在指定范围”的否定，即“且”的否定．选.．(·江西省三校联考)下列四个结论：①若>，则>恒成立；②命题“若－＝，则＝”的逆命题为“若≠，则－≠”；③“命题或为真”是“命题且为真”的充分不必要条件；④命题“对任意的∈，－>”的否定是“存在∈，－≤”．其中正确结论的个数是( )．．．．解析：选.记()＝－，>，则′()＝－≥，函数()在(，＋∞)上是增函数，因此当>时，()>()，即－>，>，①正确；命题“若－＝，则＝”的逆命题为“若＝，则－＝”，②不正确；由命题“或”为真不能得知命题“且”为真，反过来，由命题“且”为真命题可得知命题“或”为真，因此“命题或”为真是“命题且”为真的必要不充分条件，③不正确；命题“对任意的∈，－>”的否定是“存在∈，－≤”，④正确．综上所述，正确结论的个数是，故选.．(·昆明联考)若“：存在∈[，]，≤”是真命题，则实数的最小值是( )．．．－．－解析：选.问题转化为＝在∈[，]的取值范围，则∈[－，]，故选.．(·辽宁省五校联考)下列选项中，说法正确的是( )．命题“存在∈，－≤”的否定是“存在∈，－>”．命题“或为真”是命题“且为真”的充分不必要条件．命题“若≤，则≤”是假命题．命题“在△中，若<，则<”的逆否命题为真命题解析：选中命题的否定是：对任意的∈，－>，故不对；中当为假命题、为真命题时，或为真，且为假，故不对；中当＝时，，∈，故的说法正确；中命题“在△中，若<，则<”为假命题，所以其逆否命题为假命题．故选.．(·山东省实验中学第一次诊断)下列有关命题的叙述错误的是( )．若綈是的充分条件，则是綈的必要条件．若且为假命题，则，均为假命题．命题“对任意的∈，－>”的否定是“存在∈，－≤”．“>”是“<”的充分不必要条件解析：选.易知，正确；且为假，，至少有一个为假，错误；“任意”的否定是“存在”，“>”的否定是“≤”，正确；“>”一定能推出“<”，但当＝－时，满足<，但不满足>，所以“>”是“<”的充分不必要条件，正确．综上可知，选.．(·郑州调研)命题“存在∈，>”的否定是．答案：对任意的∈，≤．已知命题：存在∈，－＝，：对任意的∈，＋＋≥，若或(綈)为假命题，则实数的取值范围是．解析：若或(綈)为假命题，则假真．命题为假命题时，有≤<；命题为真命题时，有Δ＝－≤，。

1．1 集合的概念与运算一、选择题1．已知集合A ＝{0，1，2，3}，集合B ＝{(x ，y )|x ∈A ，y ∈A ，x ≠y ，x ＋y ∈A }，则B 中所含元素的个数为( )A ．3B ．6C ．8D ．102．设集合A ＝{x |(x ＋1)(x －2)<0}，B ＝{x |1<x <3}，则A ∪B ＝( )A ．{x |－1<x <3}B ．{x |－1<x <1}C ．{x |1<x <2}D ．{x |2<x <3}3．已知A ＝{x |a －1≤x ≤a ＋2}，B ＝{x |3<x <5}，则使得B ⊆A 成立的实数a 的取值范围是( )A ．(3，4]B ．[3，4]C ．(3，4)D ．∅4．(2015·湖南高三质检)若集合P ＝{x |3＜x ≤22}，非空集合Q ＝{x |2a ＋1≤x ＜3a －5}，则能使Q ⊆(P ∩Q )成立的所有实数a 的取值范围为( )A ．(1，9)B ．[1，9]C ．[6，9)D ．(6，9]5．已知U ＝⎩⎨⎧⎭⎬⎫x ∈Z y ＝ln ⎝⎛⎭⎫9x －1，M ＝{x ∈Z ||x －4|≤1}，N ＝⎩⎨⎧⎭⎬⎫x ∈N 6x ∈Z ，则集合{4，5}等于导学号74780000( )A ．M ∩NB ．M ∩(∁U N )C ．N ∩(∁U M )D ．(∁U M )∪(∁U N )答案：1．C 2.A 3.B 4.D 5.B二、填空题6．设a ，b ∈R ，集合⎩⎨⎧⎭⎬⎫a ，b a ，1＝{a 2，a ＋b ，0}，则a 2 017＋b 2 017＝________. 7．(2015·原创题)已知集合A ＝{(x ，y )|x 2＋y 2＝1}，B ＝{(x ，y )||x |＋|y |＝λ}，若A ∩B ≠∅，则实数λ的取值范围是________.导学号747800018．在整数集Z 中，被5除所得余数为k 的所有整数组成一个“类”，记为[k ]，即[k ]＝{5n ＋k |n ∈Z }，k ＝0，1，2，3，4.给出如下四个结论：①2 014∈[4]；②－3∈[3]；③Z ＝[0]∪[1]∪[2]∪[3]∪[4]；④“整数a ，b 属于同一‘类’”的充要条件是“a －b ∈[0]”．其中，正确结论的序号是________．答案：6．－1 7.[1，2] 8.①③④三、解答题9．已知集合A ＝{x |x 2－3x －10≤0}，(1)若B ⊆A ，且B ＝{x |m ＋1≤x ≤2m －1}，求实数m 的取值范围；(2)若A ⊆B ，且B ＝{x |m －6≤x ≤2m －1}，求实数m 的取值范围．解析：(1)A ＝{x |－2≤x ≤5}．∵B ⊆A ，∴①B ＝∅，则m ＋1＞2m －1，∴m <2；②B ≠∅，则⎩⎪⎨⎪⎧m ＋1≤2m －1，m ＋1≥－2，2m －1≤5，∴2≤m ≤3；综上知，m ≤3.(2)A ＝{x |－2≤x ≤5}．∵A ⊆B ，∴⎩⎨⎧2m －1＞m －6，m －6≤－2，2m －1≥5，解得⎩⎨⎧m >－5，m ≤4，m ≥3，∴3≤m ≤4.10．已知集合A ＝{x ||x －1|<2}，B ＝{x |x 2＋ax －6<0}，C ＝{x |x 2－2x －15<0}．(1)若A ∪B ＝B ，求a 的取值范围；(2)是否存在a 的值使得A ∪B ＝B ∩C ？若存在，求出a 的值；若不存在，请说明理由． 解析：A ＝{x |－1<x <3}，C ＝{x |－3<x <5}．(1)由A ∪B ＝B 知，A ⊆B ，令f (x )＝x 2＋ax －6，则⎩⎪⎨⎪⎧f （－1）＝（－1）2－a －6≤0，f （3）＝32＋3a －6≤0， 解得－5≤a ≤－1，即a 的取值范围是[－5，－1]．(2)假设存在a 的值使得A ∪B ＝B ∩C ，由A ∪B ＝B ∩C ⊆B 知A ⊆B ，由A ∪B ＝B ∩C ⊆C 知B ⊆C ，于是A ⊆B ⊆C ，由(1)知若A ⊆B ，则a ∈[－5，－1]，当B ⊆C 时，由Δ＝a 2＋24>0，知B 不可能是空集，于是⎩⎪⎨⎪⎧f （－3）＝（－3）2－3a －6≥0，f （5）＝52＋5a －6≥0，－3<－a 2<5，解得a ∈⎣⎡⎦⎤－195，1. 综合a ∈[－5，－1]知存在a ∈⎣⎡⎦⎤－195，－1满足条件．11．已知集合A ＝{x |x 2－ax ＋a 2－19＝0}，B ＝{x |x 2－5x ＋6＝0}，C ＝{x |x 2＋2x －8＝0}，是否存在实数a ，使得A ∩C ＝∅和∅A ∩B 同时成立？若存在，求出a 值；若不存在，说明理由.导学号74780002解析：由已知可求得B ＝{2，3}，C ＝{2，－4}．假设存在a 使得A ∩C ＝∅和∅A ∩B ，则由A ∩C ＝∅知，2和－4都不是方程x 2－ax ＋a 2－19＝0的根．由∅A ∩B ，知A ∩B ≠∅，∴x ＝3是方程x 2－ax ＋a 2－19＝0的根，即9－3a ＋a 2－19＝0，解得a ＝5或a ＝－2.当a ＝5时，可求得A ＝{2，3}，此时A ∩C ＝{2}，这与A ∩C ＝∅矛盾，∴a ＝5舍去．当a ＝－2时，可求得A ＝{3，－5}，满足A ∩C ＝∅和∅A ∩B .∴存在a 值，使得A ∩C ＝∅和∅A ∩B 同时成立，此时a ＝－2.。

山东省13市2017届高三最新考试数学文试题分类汇编集合与常用逻辑用语2017.03一、集合1、（滨州市2017届高三上期末）设集合{}02A x x =≤≤，{}21B x x =>，则集合AB =（ ）A ．{}01x x ≤≤B ．{}01x x x ><-或 C ．{}12x x <≤ D ．{}02x x <≤2、（德州市2017届高三第一次模拟考试）设集合{}2|230A x x x =--<，{}|ln(2)B x y x ==-，则A B =（ ）A ．{}|13x x -<<B ．{}|12x x -<<C ．{}|32x x -<<D ．{}|12x x <<3、（菏泽市2017年高考一模）若集合A={﹣2，﹣1，0，1，2}，集合B={x |lg （x +1）＞0}，则A ∩B 等于（ ）A ．{﹣1，0，1，2}B ．{﹣1，﹣2}C ．{1，2}D ．{0，1，2}4、（济宁市2017届高三第一次模拟（3月））已知全集{}1,2,3,4,5U =，{}3,4,5M =，{}2,3N =，则集合()U N M =ð（ ） A ．{}2B ．{}1,3C ．{}2,5D ．{}4,55、（聊城市2017届高三上期末）设集合，{0,1,2,3,4,5}{0,1,3}{1,2,5}U A B ===，，，则()U C A B =∩（ ）A.{2,4,5}B.{1,2,4,5}C.{2,5}D.{0,2,3,4,5}6、（临沂市2017届高三2月份教学质量检测（一模））若集合{}0A x x =≥，且A B B =I ，则集合B 可能是 （A ）{}2x x ≥（B ）{}1x x ≤（C ）{}1x x ≥-（D ）R7、（青岛市2017年高三统一质量检测）设全集2I {|9Z}x x x =<∈，，{12}A =，，{2,1,2}B =--，则 I ()A B =ðA ．{1}B ．{1,2}C ．{2}D ．{0,1,2}8、（日照市2017届高三下学期第一次模拟）已知集合{}{}0,1,2,11,M N x x x Z ==-≤≤∈，则M ∩N 为(A)()0,1(B) []0,1(C) {}0,1 (D) ∅9、（泰安市2017届高三第一轮复习质量检测（一模））已知集合{}}2230,03A x x x B x x A B =+-<=<<⋂=，则A ．(0，1)B ．(0，3)C ．(－1，1)D ．(－1，3)10、（潍坊市2017届高三下学期第一次模拟）设集合A={}2,x x n n N *=∈，B=122x x ⎧⎫⎪⎪≤⎨⎬⎪⎪⎩⎭，则A ∩B=A ．{}2B ．{}2,4C ． {}2,3,4D ．{}1,2,3,411、（烟台市2017届高三3月高考诊断性测试（一模））设集合2{90}A x x =-<，{2}B x x N =∈，则A B 中元素的个数为（ ）A ．3B ．4C ．5D ．6 12、（枣庄市2017届高三下学期第一次模拟考试）已知集合{}(){}()32,1,log 21,R A x x x B x x A C B =≥≤-=-≤⋂=或则A ．{}1x x <-B ．{}1,2x x x ≤-或＞C ．{}2,=1x x x ≥-或D ．{}1,2x x x <-≥或13、（淄博市2017届高三3月模拟考试）已知集合{}24A x x =>，{}0,1,2,3B =，则AB =（ ）A ．∅B ．{}0C ．{}0,1D ．{}0,1,2参考答案1、C2、B3、C4、D5、C6、A7、D8、C9、A 10、B 11、D 12、D 13、C二、常用逻辑用语1、（滨州市2017届高三上期末）下列说法中，不正确的是（ ） A ．“1s i n 2θ=”是“30θ=”的充分不必要条件B ．命题p ：0n N ∃∈，021000n >，则:p n N ⌝∀∈，21000n ≤C.命题“若2320x x -+=，则1x =”的逆否命题为“若1x ≠，则2320x x -+≠”D ．命题“若()0x ∀∈+∞，，则23x x <”是真命题 2、（德州市2017届高三第一次模拟考试）“22ac bc >”是“a b >”的（ ） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3、（菏泽市2017年高考一模）“m ＞1“是“函数f （x ）=3x +m ﹣3在区间1，+∞）无零点”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4、（济宁市2017届高三第一次模拟（3月））设a R ∈，“，，16为等比数列”是“4a =”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件5、（聊城市2017届高三上期末）已知,αβ是相交平面，直线l ⊂平面α，则“l β⊥”是“αβ⊥”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 6、（临沂市2017届高三2月份教学质量检测（一模））已知命题:(,0),23;xxP x ∃∈-∞＜命题:(0,),sin 1,q x x π∀∈≤则下列命题为真命题的是(A) p q ∧(B) ()p q ∨⌝(C) ()p q ∧⌝ (D) ()p q ⌝∧7、（青岛市2017年高三统一质量检测）已知R λ∈,向量()()3,,1,2a b λλ==-，则“35λ=”是“a b ⊥”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件8、（日照市2017届高三下学期第一次模拟）“()2log 231x -<”是“32x >”的 (A)充分不必要条件 (B)必要不充分条件 (C)充分必要条件(D)既不充分也不必要条件9、（泰安市2017届高三第一轮复习质量检测（一模））以下命题①“1x =”是“2320x x -+=”的充分不必要条件②命题“若23201x x x -+==，则”的逆否命题为“若21320x x x ≠-+≠，则”③对于命题2:0,10p x x x ∃>++<使得，则2:010p x x x ⌝∀≤++≥，均有 ④若p q ∨为假命题，则p 、q 均为假命题其中正确命题的序号为 ▲ (把所有正确命题的序号都填上)10、（潍坊市2017届高三下学期第一次模拟）已知命题p ：对任意x ∈R ，总有22x x >；q ：“1ab >”是“a >l ，b >l ”的充分不必要条件．则下列命题为真命题的是 A ．p q ∧ B ．p q ⌝∧ C ．p q ∧⌝ D ．p q ⌝∧⌝11、（烟台市2017届高三3月高考诊断性测试（一模））设0,a b R <∈，则“a b <”是“a b <”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件12、（枣庄市2017届高三下学期第一次模拟考试）已知R a ∈，则“0＜a ”是“函数()()()01，在∞-+=ax x x f 上是减函数”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要13、（淄博市2017届高三3月模拟考试）下列命题为真命题的是（ ）. A ．若0x y >>，则ln ln 0x y +> B ．“4πϕ=”是“函数sin(2)y x ϕ=+为偶函数”的充要条件C ．0(,0)x ∃∈-∞，使0034xx<成立D ．已知两个平面,αβ，若两条异面直线,m n 满足,m n αβ⊂⊂且//,//m n βα，则//αβ参考答案1、B2、A3、A4、B5、A6、D7、C8、A9、①②④ 10、D 11、B 12、A 13、D。

山东省2017届高三数学文一轮复习专题突破训练集合与常逻辑用语一、集合1、（2016年山东高考)设集合{1,2,3,4,5,6},{1,3,5},{3,4,5}U A B ===，则()U A B = (A ）{2,6} （B ）{3,6} （C ）{1,3,4,5} (D){1,2,4,6}2、（2015年高考)已知集合A=｛x ｜2〈x 〈4}，B=｛x ｜（x-1）（x-3）<0}，则A ⋂B=（ ）（A ）(1,3） (B ）（1,4） (C ）(2，3） (D)（2，4)3、（2014年高考)设集合},41{,}02{2≤≤=<-=x x B x x x A 则=B A（A ）（0,2] (B ） （1，2） （C ） 1，2） （D ）(1,4)4、(临沂市2016届高三11月期中质量检测)已知集合{}{}220,,,,1A x B x x x A B ==--⊆，若，则实数x 的值为A 。

1或1- B.1 C 。

1- D 。

25、（齐鲁名校协作体2016届高三上学期第二次调研联考）已知全集{0,1,2,3,4,5,6}=U ，集合2{|560}=∈-+≤A x Z x x ，集合{1,3,4,6}B ，则集合A U B （）（ )(A ） {0} （B) {2} (C ） {0,1,2,4,6} （D){0,2,3,5}6、（泰安市2016届高三二模）已知集合{{}2,20A x y B x x x ===-<,则 A ．A B ⋂=∅ B ．A B R ⋃= C ．B A ⊆ D ．A B ⊆7、（乳山市2016届高三上学期期中考试）已知集合[){}21,,10,M N x x M N =-+∞=-≤⋂=则A. []1,1- B 。

[)1,-+∞ C 。

[)1,+∞ D. ∅8、（东营市、潍坊市2016届高三高三三模）已知全集{}2,560U R A x x x ==-+≥，则U A =（ ）A ．{}2x x >B ．{}3x x <C ．{}23x x ≤≤D ．{}23x x << 9、(济宁市2016届高三三模）设集合{0,1,2,3}A =,2{30}B x xx =-<，则A B 等于（ ）A ．{}0,1B ．{}1,2C ．{}0,1,2D ．{}210、（德州市2016届高三上学期期末）已知全集U=｛0,1，2，3,4，5，6,7,8}，A={2，5,8 ｝，B=｛1,3，5，7}，则()U A B = A ．｛5｝ B ．{1，3，7}C ．{2，8｝D ．{1，3，4，5，6，7，8}11、(济宁市2016届高三上学期期末）设集合{}220A x xx =-≥，集合{}21x B x A B =>⋂=，则 A 。

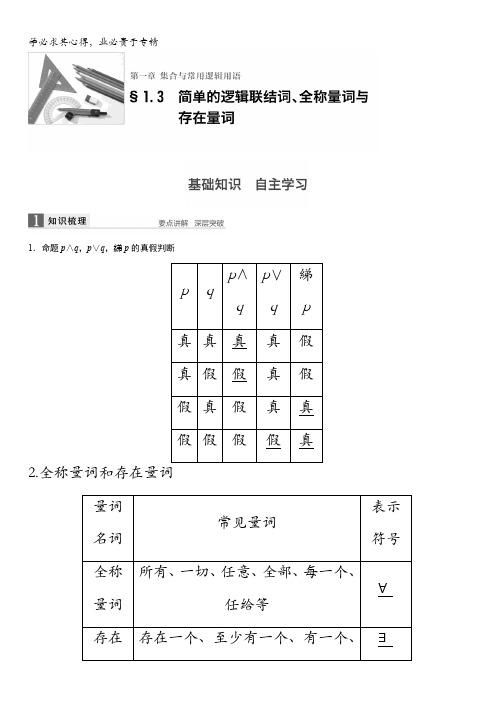
1．命题p∧q，p∨q，綈p的真假判断p q p∧qp∨q綈p真真真真假真假假真假假真假真真假假假假真2.全称量词和存在量词量词名词常见量词表示符号全称量词所有、一切、任意、全部、每一个、任给等∀存在存在一个、至少有一个、有一个、∃34判断下面结论是否正确（请在括号中打“√”或“×”) (1）命题p∧q为假命题，则命题p、q都是假命题．（×）(2)命题p和綈p不可能都是真命题．( √）(3)若命题p、q至少有一个是真命题，则p∨q是真命题．( √)（4）全称命题一定含有全称量词，特称命题一定含有存在量词．( ×）(5）写特称命题的否定时，存在量词变为全称量词．（√）(6)∃x0∈M，p（x0)与∀x∈M，綈p(x）的真假性相反．( √)1．设命题p：函数y＝sin 2x的最小正周期为错误!；命题q：函数y＝cos x的图象关于直线x＝错误!对称，则下列判断正确的是( ) A．p为真B．綈q为假C．p∧q为假D．p∨q为真答案C解析函数y＝sin 2x的最小正周期为错误!＝π，故命题p为假命题;x ＝错误!不是y＝cos x的对称轴,命题q为假命题，故p∧q为假．故选C。

2．已知命题p：对任意x∈R，总有｜x｜≥0；q：x＝1是方程x＋2＝0的根．则下列命题为真命题的是( ）A．p∧（綈q) B．（綈p）∧qC．(綈p)∧(綈q）D．p∧q答案A解析由题意知，命题p为真命题，命题q为假命题,故綈q为真命题，所以p∧(綈q)为真命题．3．（2015·浙江）命题“∀n∈N＊，f（n)∈N*且f(n)≤n”的否定形式是（)A．∀n∈N＊，f（n)∉N*且f（n）＞nB．∀n∈N*，f（n)∉N*或f(n)＞nC．∃n0∈N*，f(n0)∉N＊且f（n0)＞n0D．∃n0∈N＊，f(n0)∉N*或f(n0）＞n0答案D解析写全称命题的否定时,要把量词∀改为∃，并且否定结论,注意把“且"改为“或"．故选D。

大一轮复习数学（文) 第一章集合与常用逻辑用语1．集合与元素（1）集合中元素的三个特征：确定性、互异性、无序性．(2)元素与集合的关系是属于或不属于两种，用符号∈或∉表示．(3）集合的表示法：列举法、描述法、图示法．（4）常见数集的记法集合自然数集正整数集整数集有理数集实数集符号NN＊(或N＋）Z Q R2.关系自然语言符号语言Venn图子集集合A 中所有元素都在集合B中(即若x∈A，则x∈B）A⊆B（或B⊇A)真子集集合A是集合B的子集，且集合B中至少有一个元素不在集合A中A B（或B A)集合相等集合A，B中元素相同或集合A，B互为子集A＝B3。

集合的运算集合的并集集合的交集集合的补集图形符号A∪B＝｛x｜x∈A或x∈B｝A∩B＝{x|x∈A且x∈B｝∁U A＝{x｜x∈U，且x∉A｝4.（1)若有限集A中有n个元素，则A的子集个数为2n个，非空子集个数为2n－1个,真子集有2n－1个．（2）A⊆B⇔A∩B＝A⇔A∪B＝B.【思考辨析】判断下面结论是否正确（请在括号中打“√”或“×”）(1){x｜y＝x2＋1}＝{y|y＝x2＋1}＝{(x，y）｜y＝x2＋1}．（×）（2）若{x2，1｝＝{0,1｝，则x＝0，1.( ×）(3）｛x｜x≤1｝＝{t｜t≤1}．( √)（4）对于任意两个集合A，B，关系(A∩B)⊆(A∪B）恒成立．（√)（5）若A∩B＝A∩C，则B＝C.( ×）(6)含有n个元素的集合有2n个真子集．( ×)1．（2015·四川)设集合A＝{x|－1＜x＜2}，集合B＝｛x|1＜x＜3｝，则A∪B等于( ）A．{x｜－1＜x＜3｝B．{x｜－1＜x＜1}C．｛x｜1＜x＜2｝D．{x｜2＜x＜3}答案A解析借助数轴知A∪B＝{x|－1＜x＜3｝．2．已知集合A＝{x｜x2－x－2≤0},集合B为整数集，则A∩B等于（)A．｛－1，0,1,2} B．{－2,－1，0，1}C．｛0,1} D．｛－1，0｝答案A解析因为A＝｛x|x2－x－2≤0}＝{x｜－1≤x≤2}，又因为集合B 为整数集,所以集合A∩B＝{－1,0,1，2｝，故选A。

【创新设计】2017版高考数学一轮复习第一章集合与常用逻辑用语阶段滚动检测理北师大版(建议用时：40分钟)一、选择题1.(2016·成都诊断)已知集合A＝{x|x≤1}，B＝{x|x2－2x＜0}，则A∩B等于( )A.(0，1]B.[1，2)C.(0，1)D.(0，2)解析因为B＝{x|x2－2x＜0}＝{x|0＜x＜2}，所以A∩B＝{x|0＜x≤1}，故选A.答案 A2.(2015·郑州质量预测)集合U＝{1，2，3，4，5，6}，A＝{2，3}，B＝{x∈Z|x2－6x＋5＜0}，则∁U(A∪B)等于( )A.{1，5，6}B.{1，4，5，6}C.{2，3，4}D.{1，6}解析化简知B＝{x∈Z|1＜x＜5}＝{2，3，4}，∴A∪B＝{2，3，4}，∴∁U(A∪B)＝{1，5，6}.答案 A3.命题“存在x∈∁R Q，x3∈Q”的否定是( )A.存在x∉∁R Q，x3∈QB.存在x∈∁R Q，x3∉QC.任意x∉∁R Q，x3∈QD.任意x∈∁R Q，x3∉Q解析根据特称命题的否定为全称命题知，选D.答案 D4.(2016·日照一模)设a，b为实数，命题甲：a＜b＜0，命题乙：ab＞b2，则命题甲是命题乙的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件解析由a＜b＜0，可得ab－b2＝(a－b)b＞0，即ab＞b2，当a＝2，b＝1时，ab＞b2，显然a＜b＜0不成立，故选A.答案 A5.(2016·东北三省三校联考)已知集合A＝{0，b}，B＝{x∈Z|x2－3x＜0}，若A∩B≠∅，则b等于( )A.1B.2C.3D.1或2解析由题意知B＝{1，2}，∵A∩B≠∅，∴b＝1或2.答案 D6.(2016·芜湖一调)设全集U＝R，M＝{x|x2＞4}，N＝{x|x＜1或x≥3}都是U的子集，则图中阴影部分所表示的集合是( )A.{x|－2≤x＜1}B.{x|－2≤x≤2}C.{x|1＜x≤2}D.{x|x＜2}解析图中阴影部分表示N∩(∁U M)，M＝{x|x2＞4}＝{x|x＞2或x＜－2}，∴∁U M＝{x|－2≤x≤2}，∴N∩(∁U M)＝{x|－2≤x＜1}.答案 A7.(2015·唐山模拟)命题p：存在x0∈N，x30＜x20；命题q：任意a∈(0，1)∪(1，＋∞)，函数f(x)＝log a(x－1)的图像过点(2，0)，则( )A.p假q真B.p真q假C.p假q假D.p真q真解析∵x3＜x2，∴x2(x－1)＜0，∴x＜0或0＜x＜1，故命题p为假命题，易知命题q为真命题，选A.答案 A8.(2016·沈阳质量监测)设直线l1：2x－my＝1，l2：(m－1)x－y＝1，则“m＝2”是“l1∥l2”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件解析因为当l1∥l2时，－2＋m(m－1)＝0，解得m＝2或m＝－1，所以“m＝2”是“l1∥l2”的充分不必要条件，故选A.答案 A9.已知两个非空集合A＝{x|x(x－3)＜4}，B＝{x|x≤a}，若A∩B＝B，则实数a的取值范围是( )A.(－1，1)B.(－2，2)C.[0，2)D.(－∞，2)解析解不等式x(x－3)＜4，得－1＜x＜4，所以A＝{x|－1＜x＜4}；又B是非空集合，所以a≥0，B＝{x|0≤x≤a2}.而A∩B＝B⇔B⊆A，借助数轴可知a2＜4，解得0≤a＜2，故选C.答案 C10.(2016·长沙模拟)下列命题中，真命题是( )A.存在x∈R，|x|≤0B.任意x∈R，e x＞x eC.a －b ＝0的充要条件是a b＝1 D.若p 且q 为假，则p 或q 为假解析 B 选项：当x ＝e 时，e e＝e e，∴B 错误；C 选项：当a ＝b ＝0时，满足a －b ＝0，但不满足a b＝1，∴C 错误；D 选项：若p 且q 为假，则p ，q 至少有一个为假，当p 真q 假或p 假q 真时，p 或q 为真，∴D 错误.答案 A11.(2016·遵义省级市范高中联考)下列说法不正确的是( ) A.命题“若x ＞0且y ＞0，则x ＋y ＞0”的否命题是假命题 B.任意a ＞0，函数f (x )＝ln 2x ＋ln x －a 有零点 C.两个三角形全等是这两个三角形面积相等的必要条件 D.α＜0时，幂函数y ＝x α在(0，＋∞)上单调递减解析 对于A ，“若x ＞0且y ＞0，则x ＋y ＞0”的逆命题为“若x ＋y ＞0，则x ＞0且y ＞0”显然为假命题，所以其否命题是假命题；对于B ，令ln x ＝t ，任意a ＞0，对于方程t 2＋t －a ＝0，Δ＝1－4(－a )＞0，方程恒有解，故满足条件；对于C ，由两个三角形的面积相等不能得知这两个三角形全等，因此选项C 不正确；对于D ，显然正确. 答案 C12.ax 2＋2x ＋1＝0至少有一个负实根的充要条件是( ) A.0＜a ≤1 B.a ＜1C.a ≤1D.0＜a ≤1或a ＜0解析 法一 当a ＝0时，原方程为一元一次方程2x ＋1＝0，有一个负实根. 当a ≠0时，原方程为一元二次方程，有实根的充要条件是Δ＝4－4a ≥0， 即a ≤1.设此时方程的两根分别为x 1，x 2， 则x 1＋x 2＝－2a ，x 1x 2＝1a，当只有一个负实根时，⎩⎪⎨⎪⎧a ≤1，1a＜0⇒a ＜0；当有两个负实根时，⎩⎪⎨⎪⎧a ≤1，－2a ＜0，⇒0＜a ≤1.1a ＞0综上所述，a ≤1.法二 (排除法)当a ＝0时，原方程有一个负实根，可以排除A ，D ； 当a ＝1时，原方程有两个相等的负实根，可以排除B. 答案 C 二、填空题13.(2016·合肥质检)若全集U ＝{0，1，2，3，4，5}且∁U A ＝{x ∈N *|1≤x ≤3}，则集合A 的真子集共有________个.解析 求出集合后求解真子集.由题意可得A ＝{0，4，5}，所以集合A 的真子集有23－1＝7(个). 答案 714.若命题“存在x ∈R ，使得x 2＋(a －1)x ＋1＜0”是真命题，则实数a 的取值范围是________.解析 ∵“存在x ∈R ，使得x 2＋(a －1)x ＋1＜0”是真命题， ∴Δ＝(a －1)2－4＞0，即(a －1)2＞4， ∴a －1＞2或a －1＜－2， ∴a ＞3或a ＜－1.答案 (－∞，－1)∪(3，＋∞)15.若x <m －1或x >m ＋1是x 2－2x －3>0的必要不充分条件，则实数m 的取值范围是________. 解析 由已知易得{x |x 2－2x －3>0}{x |x <m －1或x >m ＋1}，又{x |x 2－2x －3>0}＝{x |x <－1或x >3}，∴⎩⎪⎨⎪⎧－1≤m －1，m ＋1<3或⎩⎪⎨⎪⎧－1<m －1，m ＋1≤3，∴0≤m ≤2. 答案 [0，2]16.设命题p ：方程x 2＋2mx ＋1＝0有两个不相等的正根；命题q ：方程x 2＋2(m －2)x －3m ＋10＝0无实根.则使p 或q 为真，p 且q 为假的实数m 的取值范围是________.解析 设方程x 2＋2mx ＋1＝0的两根分别为x 1，x 2，由⎩⎪⎨⎪⎧Δ1＝4m 2－4＞0，x 1＋x 2＝－2m ＞0，得m ＜－1，所以命题p 为真时：m ＜－1.由方程x 2＋2(m －2)x －3m ＋10＝0无实根，可知Δ2＝4(m －2)2－4(－3m ＋10)＜0，得－2＜m ＜3，所以命题q 为真时：－2＜m ＜3.由p 或q 为真，p 且q 为假，可知命题p ，q 一真一假， 当p 真q 假时，⎩⎪⎨⎪⎧m ＜－1，m ≥3或m ≤－2，此时m ≤－2；当p 假q 真时，⎩⎪⎨⎪⎧m ≥－1，－2＜m ＜3，此时－1≤m ＜3，所以所求实数m的取值范围是(－∞，－2]∪[－1，3). 答案(－∞，－2]∪[－1，3)。

1．四种命题及相互关系2．四种命题的真假关系(1)两个命题互为逆否命题,它们有相同的真假性；（2)两个命题互为逆命题或互为否命题，它们的真假性没有关系．3．充分条件与必要条件(1）如果p⇒q，则p是q的充分条件，同时q是p的必要条件；(2)如果p⇒q,但q p，则p是q的充分不必要条件；(3)如果p⇒q，且q⇒p，则p是q的充要条件;（4)如果q⇒p，且p q，则p是q的必要不充分条件；（5)如果p q，且q p，则p是q的既不充分又不必要条件．【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)（1）“x2＋2x－3<0”是命题．（×)(2）命题“α＝错误!,则tan α＝1”的否命题是“若α＝错误!，则tan α≠1"．（×）（3）若一个命题是真命题，则其逆否命题是真命题．（√) (4）当q是p的必要条件时，p是q的充分条件．（√)(5）当p是q的充要条件时,也可说成q成立当且仅当p成立．( √）（6)若p是q的充分不必要条件,则綈p是綈q的必要不充分条件．（√）1．（2015·山东）若m∈R，命题“若m〉0,则方程x2＋x－m＝0有实根”的逆否命题是（）A．若方程x2＋x－m＝0有实根，则m＞0B．若方程x2＋x－m＝0有实根,则m≤0C．若方程x2＋x－m＝0没有实根，则m＞0D．若方程x2＋x－m＝0没有实根，则m≤0答案D解析原命题为“若p,则q”,则其逆否命题为“若綈q，则綈p”．∴所求命题为“若方程x2＋x－m＝0没有实根，则m≤0”．2．已知命题p ：若x ＝－1，则向量a ＝（1，x ）与b ＝(x ＋2，x )共线，则在命题p 的原命题、逆命题、否命题、逆否命题中,真命题的个数为（ )A ．0B ．2C ．3D ．4答案 B解析 向量a ，b 共线⇔x －x (x ＋2）＝0⇔x ＝0或x ＝－1，∴命题p 为真，其逆命题为假，故在命题p 的原命题、逆命题、否命题、逆否命题中,真命题的个数为2。

集合与逻辑02解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)1．已知命题p ：“”；命题q ：“”．若命题“”是真命题，求实数a 的取值范围．【答案】p ：∵，∴，即；q ：∵，∴得或． 若“”是真命题，则p 真q 真，∴或．2．已知集合，,定义为集合中元素之和，求所有的和。

【答案】.3．已知命题p ：方程a 2x 2＋ax －2＝0在－1，1上有解；命题q ：只有一个实数x满足不等式x 2＋2ax ＋2a ≤0，若命题“p 或q ”是假命题，求a 的取值范围．【答案】由题意知a ≠0，若命题p 正确，由于a 2x 2＋ax －2＝(ax ＋2)(ax －1)＝0.∴x ＝1a 或x ＝－2a． 若方程在－1，1上有解，满足－1≤1a ≤1或－1≤－2a≤1， 解之得a ≥1或a ≤－1.若q 正确，即只有一个实数x 满足x 2＋2ax ＋2a ≤0.则有Δ＝0，即a ＝0或2.若p 或q 是假命题．则p 和q 都是假命题，有⎩⎨⎧－1＜a ＜1，a ≠0且a ≠2.所以a 的取值范围是(－1，0)∪(0，1)．2[1,2],0x x a ∀∈-≥2,220x R x ax a ∃∈++-=p q ∧2[1,2],0x x a ∀∈-≥2min (),[1,2]a x x ≤∈1a ≤2,220x R x ax a ∃∈++-=2(2)4(2)0a a ∆=--≥2a ≤-1a ≥p q ∧2a ≤-1a ={}12,11,9,7,6,0,4,5--=A A X ⊆)(x S X )(x S S 46082)1211976045(7=⨯++++++--=S4．已知 且； q ：集合且.若∨为真命题，∧为假命题，求实数的取值范围.【答案】对p ：所以． 若命题p 为真，则有 ；对q ：∵且∴若命题q 为真，则方程无解或只有非正根．∴或, ∴∵p, q 中有且只有一个为真命题∴ (1) p 真，q 假：则有； (2) p 假，q 真：则有； ∴或．21．记函数f （x ）＝lg （x 2一x 一2）的定义域为集合A ，函数g （x的定义域为集合B ．(1）求AB ；(2）若C ＝｛x ｜x 2＋4x ＋4一p 2＜0，p ＞0｝，且C ，求实数p 的取值1:(),3x p f x -=|()|2f a <}0x |x {B },R x ,01x )2a (x |x {A 2>=∈=+++=∅=⋂B A p q p q a 1|()| ||23a f a -=<75<<-a }0x |x {B >=∅=⋂B A 01x )2a (x )x (g 2=+++=04)2a (2<-+=∆0(0)0202g a ⎧⎪∆≥⎪≥⎨⎪+⎪-<⎩4a ->4a 54a 7a 5-≤<-⎩⎨⎧-≤<<-，即有7a 4a 5a 7a ≥⎩⎨⎧->-≤≥，即有或4a 5-≤<-7a ≥()A B ⊆范围．【答案】(1）(2）22．已知集合A ＝{x |x ＝m 2－n 2，m ∈Z ，n ∈Z }．求证：(1)3∈A ； (2)偶数4k －2(k ∈Z )不属于A .【答案】 (1),(2)设，则存在,使成立，即.当m ，n 同奇或同偶时，m －n ，m ＋n 均为偶数，∴(m －n )(m ＋n )为4的倍数，与4k －2不是4的倍数矛盾． 当m ，n 一奇，一偶时，m －n ，m ＋n 均为奇数，∴(m －n )(m ＋n )为奇数，与4k －2是偶数矛盾．∴4k －2∉A .22123-= A ∈∴3A k ∈-24Z n m ∈,2224n m k -=-24))((-=+-k n m n m。