当前位置：文档之家 › 平板波导理论

平板波导理论

  • 格式：doc
  • 大小：1014.00 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

第4章多层平板波导

第4章多层平板波导
• 式（ 4 . 19 ）可约化为如下形式：
2020年1月22日星期三 共 UP
DOWN
BACK
• 4 . 1 . 2 非对称多层平板波导
2020年1月22日星期三 共 UP
DOWN
BACK
• 对于如图 4 . 3 所示的非对称 l 十 2 层平板波导，只 要推广 4 . 1 . 1 节的结果，便可得到 TE 波的矩阵形 式的模式本征方程:
射率差决定。折射率差大，则Φ (s)也大；折 射率差小，则Φ (s)也小。
• 综合上述分析，可得以下重要结论：对多层平 板波导，不仅要考虑主波的相位贡献，而且要 考虑层间反射子波的相位贡献。
2020年1月22日星期三 共 UP
DOWN
BACK
2020年1月22日星期三 共 UP
DOWN
BACK
• 2 场匹配理论 设横向电场分布为
2020年1月22日星期三 共 UP
DOWN
BACK
p.23
2020年1月22日星期三 共 UP
DOWN
BACK
2020年1月22日星期三 共 UP
DOWN
BACK
• 而方程（ 4 . 19 ）中左边第二、三项前的振幅 分别是主波从 n1 介质射向 n2介质和主波从n2介 质射向 nl 介质时的反射系数。可见这两项代表 波导传输的反射子波。主波与反射子波的相干 叠加构成了四层波导中的导波.
第四章 多层平板波导
黄衍堂
2020年1月22日星期三
1
第４章 多层平板波导
由于多层平板波导在模场分布、模式截止和功率约 束等方面具有许多独特的性质，因此，这种结构在半 导体激光器、光波导定向藕合器、光波导偏振器等波 导器件中有着重要的应用。本章首先分析非对称平板 波导的色散性质，然后再讨论对称多层平板波导及其 重要特性，最后，利用传输型色散方程和微扰理论分 析平板藕合波导及其重要性质。

平板介质光波导理论

平板介质光波导理论

(3,1 －5a )
(3.1 - 5b )
可以得出：Hy = Ex = 0 因此，只有y方向电场存在 利用分离变量法对波动方程(3.1 – 13)求解，便可得到平板 介质波导的场模表示式为
E y(x, z,t) E y(x)exp j t z
其中Ey(x)及模传播常数满足
(3.2 – l)
(3.1 - 12) (3.1 - 13)
(3.1 - 14)
• 最简单的情况是设光波的电矢量 沿y方向偏振、沿z方向传播的平 面电磁波，即有 • E = Ey、Ex = Ez = 0。
• Ey在z方向以角频率 = 2发生 周期变化， • 因为只在z方向有空间变化，故 有/x = /y = 0 • 由式(3.1 – 13)可以得到以z和t作 为函数的Ey：
3.1 光波的电磁场理论
• 一、基本的电磁场理论
•
麦克斯韦方程组
B E t D H J t B 0
(3,1 －1a )
(3.1 - 1b ) (3.1 - 1c ) (3.1 - 1d )
D
• 设介质是均匀且各向同性的，且假设在低场强下不足以 产生非线性效应，并且不考虑在半导体介质中实际存在 的色散效应，而认为和与光波的频率无关。 (3.1 - 3a ) D E
第三章 平板介质光波导理论
引言 3.1 光波的电磁场理论 3.2 光在平板介质波导中的传输特性
引言
• 从理论上说，平板介质光波导是一种最简单的光波导形式， 可以运用电磁场的基本理论，将平板介质波导处理为边界 条件，从而得到数学上简单、物理上容易理解的基本光波 导的有关方程。一旦熟悉了这种介质光波导的一般方法， 就不难从数学上深入认识圆形光波导（如光纤）和其它形 状的光波导． • 分析介质波导的一般方法是根据介质波导的边界条件求解 麦克斯韦方程，得出有关光场传播模式的表示式； • 传播模式可以分为偶阶的和奇阶的横电波（ TE ）和横磁 波 ( TM ) ； • 由传播模式的本征方程或特征方程得出与模有关的传播常 数。然后求出传输模的截止条件、相位延迟等与波导有关 的参数， • 分析平板介质波导的实际意义在于，许多半导体光电子器 件和集成光学是以平板介质波导作为工作基础的。如，异 质结半导体激光器和发光二极管正是利用异质结所形成的 光波导效应将光场限制在有源区内并使其在输出方向上传 播。

光波导理论PPT

光波导理论PPT

模式所携带的能量基本上限制在导波层内，因此被成为束
缚模或导模。
③对于 k0n2 k0n0，图（2）中的d范围，方程 （1.4）解对应于覆盖层中的指数函数、导波层和衬底中的 振荡函数，这些模式称为衬底辐射模。
④对于 0 k0n2 ，图（2）中的（e）范围，方程 （1.4）的解在波导的三层介质中都是振荡函数，这类模式 称为辐射模或包层模。
(k1h)
1 p2
0
（2.11）
解之，可得
tan(k1h)
p0 p2
k1 (1
p0 p2 k12
)
（2.12）
式（2.12）为TE波的相位型色散方程，式（2.11）称为矩
阵形式的TE波的模式本征方程。
对于一般非对称n+2层平板波导，推广上述的结果，便 可得到TE波的矩阵形式的模式本征方程
在分界面上连续，所以最后的场分布如图2（a）所示。
场随着离开波导两界面的距离而无限制增加，这个解在物
理上是不能实现的，因此它并不对应于真实的波。
②对于 k0n0 两点的情况，因为
k0
1 Ey
n21xE2，y 对0，应由于方图程（（2）1.中4）（可b）知，和导（波c）层
中的解是正余弦形式，其余区域为指数形式的。由于这些
1b
1b
前面分析得到导模截止时，b=0,所以可得模式归一化截止 频率
Vcut m arctan a, m 0,1,2, 由上式可知波导进行单模传输的条件为
arctan a V arctan a
（1.26） （1.27）
对于完全对称波导（衬底与覆盖层的折射率相等）， a=0,此时的模式归一化截止频率
k0n0
N n0
②波导的归一化频率

多层平板波导[wsg]

多层平板波导[wsg]

特征方程：
2 K 2d
五层平板波导
x2 n2 n1 n0 n-1 n-2 d+ 2a d-
x1 x0 x-1 x-2
各区场解为（中心层为振荡区，其余各层为指数解）：
＋ 2＝ A＋ 0 cos ＋ 0
1＝ 0＝ 0＝ 1＝
2a x 2a 2d
exp[ p 3 ( x 2 a 2 d )]
p3 p4 K2 2 K 1 a m arctan C 14 ＋ arctan C 12 tan arctan C 23 K1 K1 K2
(TE 模）
C ij ( n i /n j )
(TM 模）
由 （TE模）或n-2 （TM模）的连续条件可得模式方程
2 K 0 a m arctan[ C 01 arctan[ C 0 1 p 1 K0 p 1 K0 tanh( ar tanh C 12 p2 p 1 p 1 d 1 )] p 1 d 1 )]
A 0 cos K 0 ( x a ) 0 A 0 cos 0 A 0 cos 0
A＋ 0 cos K 0 ( x a ) 0
cosh[ p 1 ( x x 1 ) 1 ] cosh 1 cosh[ p 1 d 1 1 ] cosh 1 exp[ p 2 ( x x 2 )]
2y E y 0 H x dE y j 0 H z dx dH z j E y j H x dx
方程组2： (TM模） ＝ H

第二章-理想平板介质光波导中的光传播特性及仿真

第二章-理想平板介质光波导中的光传播特性及仿真

第2章介质光波导分析方法2.1 平板介质光波导一般概念2.1 平板介质光波导一般概念波动理论法则是把平板介质光波导中的光波看作是满足波导边界条件的麦克斯韦方程组的解。

2.2 平板光波导分析的射线法振幅反射率和附加相移振幅反射率和附加相移S 波（TE 波——电矢量平行于界面）振幅反射率：光传播过程相位变化：光波不仅在介质中传播过程中相位会发生改变，在界面上反射时相位也会变化。

对于θ1 ＜ θ1c ，界面上发生全反射，此时上式的分子和分母中第二个平方根内为负数，因此得到的振幅反射率r 为复数。

1.106分子分母同乘k ）振幅反射率和附加相移振幅反射率和附加相移s 波（ TE波——电矢量平行于界面） 附加相移为：p 波（ TM波——磁矢量平行于界面）在界面发生全反射时引起的附加相移为：（1.145）（1.144）界面：n1、n2、n3的界面，不是入射面平板波导中的其他光场均可视为TEM 模：模式只有横向分量，而无纵导模特征方程导模特征方程入射光线两次反射后与入射光线同方向传输特征方程特征方程A、B 两点的距离为:C、D两点的距离为:光线CD 还经历了两个附加相移:分别是介质1、3 界面处全反射的附加相移ϕ3 和介质1、2 界面处全反射的附加相移ϕ2.平板光波导的特征方程：特征方程特征方程 界面处的附加相移会因入射光偏振方向的不同而有所差异，因此就能够得到两个不同模式下的特征方程电矢量平行于界面的导波式中：特征方程特征方程同样地，磁矢量平行于界面的导波TM 模的特征方程（代入ΦM2和ΦM3） ：这里采用的是简单光线传播的射线理论。

实际上，从麦克斯韦方程出发，结合介质界面处的边界条件也可以推导出以上特征方程。

引入的几个重要参数——都是θ的函数,得到一个光波模式的波矢就可以求解其他引入的几个重要参数——都是θ的函数,得到一个光波模式的波矢就可以求解其他纵向波矢横向波矢衰减系数< n 1kn 2k << n 1k2.3 平板光波导中的TE模TE模的电磁理论求解TE模的电磁理论求解平板光波导中的TE模仅有E y由麦克斯韦方程：(2.30)TE模的电磁理论求解TE模的电磁理论求解的式子因此可以将H的分量表示为Ey代入式(2.30)，可以得到关于Ey的波动方程，j = 1;2;3 表示分别是在芯层、衬底和覆盖层。

1.2-介质板波导

1.2-介质板波导
( x d )
k k0 n2
应有K 2 k0 2 n2 2 2 0, 令 2 2 k0 2 n2 2
D ( x d ) e i D x ( x d ) ( )e x
12
（3） 边界条件和特征方程式
当x d 时, 应有E y1 E y 2 , H z1 H z 2 A(1 K
1.2 介质平板波导
1
主要内容
1.
基本波动方程和波导方程式
2.
3.
对称介质平板波导的传输模式
介质板波导中的多模群时延
2
1、波动方程和波导方程式
1）波动方程：由麦克斯韦方程组推导出
B E t E ( B ) t D 2 ( E ) E ( ) t t D ( E ) E E 0 E E
准备2
i E z H z Ex 2 ( ) K x y i H z E z Hx ( ) 2 K x y i E z H z E y 2 ( ) K y x i H z E z Hy ( ) 2 K y x K 2 k 2 2 2 2
两个平面波的传输方向与介质板的法线夹角
tan

K
在介质板上，两个平面波满足内部全反射条件， 它们对介质板入射角度是由模式传输矢量的分量β、K所决定。
21 结论：模式截止的情况与以临界角入射到介质板上的平面波相对应
3）TM模式（以TE分析类似） 3.介质板波导中的多模群时延
d dL dH K 2 k0 2 n12 2 f 0
得 令

平板光波导

k0n f max( k0ns , k0nc )
根据边界条件，在x=a,-a处，有 E y , H z 连续（E y 和它的偏导数）
tan(ha ) q
h
tan(ha ) p
h
h(2a) m arctan(q ) arctan(p )
h
h
这就是TE模的特征方程
13
类似地，再研究TM模
To explain metal’s dispersion regulation, another more precise mode was demonstrate called Drude mode.
Where,
()
p2 2 i
p
Is totally caused by the transition of
令
2 1
k021
2
2 2
2
k02 2
在X=a处利用
1
dH y (x) dx
可以得到
tan( 1a)
1 2 2 1
T
1a m arctan(T )
16
对于奇对称的情况：
Hy(x)
Asin(1a)e 2 (xa) , x a Asin(1x),| x | a Asin(1a)e 2 (xa) , x a
2h 212 210
5
如果相干相长，即满足谐振条件，则此入射角对应的光 线（模式）可以被导波所接受
2h 212 210 2m
物理意义：在波导厚度h确定的情况下，平板波导所能 维持的导模模式数量是有限的，此时m只能取有限个整 数值，这个方程也称作平板波导的本征方程
每一模式对应的锯齿光路和横向光场分布
6
对于特征方程中的 12 10 是上下界面处全反射所引起的相移，那 么具体可根据菲涅尔公式求出。

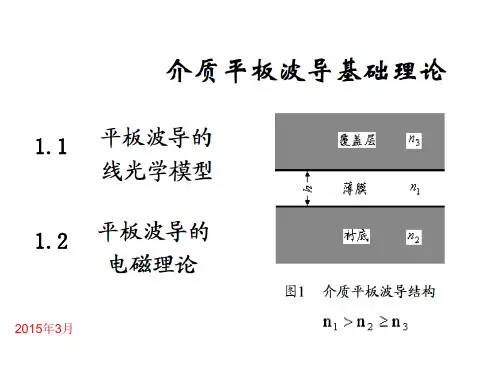
2-平板波导的电磁理论

即电场垂直于波传播方向的模式。
ε =ε = k0 ω = ε 0 µ0 2π / λ 0n ，
2
j = 1, 2,3
TE波的波动方程：
E ( x, z , t ) E ( x) exp[i (z t )] H ( x, z , t ) H ( x) exp[i (z t )]
2 3 2 2
NTE
1 2 2 n2 n3 (Vc arctan 2 2 ) n n 1 2 int
N total NTE NTM
小结：波动光学方法
• 波动理论是一种比几何光学方法更为严 格的分析方法,其严格性在于:(1)从光波的 本质特性──电磁波出发,通过求解电磁波 所遵从的麦克斯韦方程,导出电磁场的场 分布,具有理论上的严谨性;(2) 未作任何 前提近似,因此适用于各种折射率分布的 单模光和多模光波导。
光波导技术的广阔应用领域光波导技术有源无源器件光纤通信干线光交换接入网aondwdmoadmotdmfttcboh位移振动温度压力应变应力电流电压电场磁场流量浓度可以测量70多个物理化学量广告显示牌激光手术刀仪表照明工艺装饰电力输送光纤面板医用内窥镜潜望镜光子集成光电子集成集成光路光收发模块光接入模块光开关模块光放大模块信息获取信息传输信息处理其它应用作业
1. 波导的有效折射率 N
定义： 由于： 所以：
N / k0 k0 n2 k0 n1
n2 N n1
k0 n2
N n2
波导中导模截止条件： 指数衰减场
2. 波导的归一化频率V
2 1/2 V k0 h(n12 n2 )
V ( , h, n)的物理意义？
广告显示牌 激光手术刀 仪表照明 工艺装饰 电力输送 光纤面板 医用内窥镜 潜望镜

集成光学ppt课件 第二章第2节 平板波导的射线光学理论




而12 0
TE波的色散方程变为
1
w k0 n 1 2n2 2marctan n n 1 2 2 2 n n3 2 2 2 2,m 0,1 ,2
故某一模式的截止波长为
w
cTE2
1 n12n22
marctann n122 2 n n3 22 21 2
T E 模
n 1 2 n e 2 ff 1 2k 0 w m a rc ta n n n 1 2 2 2 n n 1 e 2 2 ff n n e 2 f2 f 2 1 2 a rc ta n n n 1 3 2 2 n n 1 e 2 2 ff n n e 2 f3 2 f 1 2
§2.2平板波导的射线光学理论
• 2.2.1光波导的分类 • (a)平板波导(slab waveguide) • (b)条形波导(strip waveguide) • (c)圆柱波导(cylindrical waveguide)
平板波导
n3cladding
n1 core n2substract
c 1 3 i c 1 2 时 ， 形 成 衬 底 辐 射 波 ；
i c 1 2 且 c 1 3 时 ， 形 成 传 导 波 或 导 行 波 。
2.2.2 用射线方法研究平板光波导的导模
h n1 k0

1. 波矢的横向分量
把波矢分解为平行于波导的分量（相位常数为β）和垂直 于波导的分量（相位常数为h），三者关系为：
T M 模
如何理解模的概念？
(1)模式是光波导中一个常用的概念。 (2)从数学方面理解，模式是满足亥姆霍兹方程其在波导中心

1.1平板波导几何光学分析1102


1 1
1 1
导模
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
波导的n1、n2界面的全反射临界角 波导的n1、n3界面的全反射临界角 因为 n2 n3，所以 C12 C13
C 12 arcsin
C 13 arcsin
n2 n1
n3 n1
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
X 覆盖层 薄膜层 衬底层
Z
n3 n1 n2
Y
平板波导
Z-光波传输方向
从物理量随着指标变化来看，平板波导只与X、Z两 个指标波导。又可称平板波导为二维波导。
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
设n1 > n2 n3
n2= n3－对称平板波导； n2 n3－非对称平板波导；
sin 1 sin C 12 sin C 13
将
sin C 12
n2 n1
代入
n1sin 1 n2
n2 sin1 n1
k0n1sin 1 k0n2
而传播常数
k1z k0 n1 sin 1
n2 k0
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
1、导模 （1）传播常数 因为是导模，所以 1 > C12 C13， 定义：传播常数－薄膜层中，沿Z方向的波数。
k1z k0 n1 sin 1
n1k0
1
Z
＝k1z =n1k0 sin1
§1.1 平板波导几何光学分析 2011年2月

第一章 平板波导
覆盖层中，
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第一章平板波导的射线理论光束在介质中传输时，由于介质的吸收和散射而引起损耗，由于绕射而引起发散，这些情况都会导致光束中心部分的强度不断地衰减。

因此，有必要设计制作某种器件，它能够引导光束的传播，从而使光束的能量在横的方向上受到限制，并使损耗和噪声降到最小，这种器件通常称为光波导，简称波导。

结构最简单的波导是由三层均匀介质组成的，中间的介质层称为波导层或芯层，芯两侧的介质层称为包层。

芯层的介电常数比芯两侧包层的介电常数稍高，使得光束能够集中在芯层中传输，因而起到导波的作用。

这种波导的介电常数分布是陡变的，也称为阶梯变化的，常称这种波导为平板波导。

对光波导特性的分析，应用两种理论，即射线光学理论和波动光学理论。

射线光学理论的优点是对平板波导的分析过程简单直观，对某些物理概念能给出直观的物理意义，容易理解。

缺点是对于结构复杂的多层波导射线光学理论不便于应用，或只能得出粗糙的结果。

一般而言，若想全面、正确地分析各种结构的光波导的模式特性，还必须采用波动理论。

光射线，简称射线或光线，可以这样理解：一条很细很细的光束，它的轴线就是光射线。

它的方向沿着光能流的方向。

光线与光束是不同的，光线是无限细的，光束则有一定的尺寸。

光线在均匀介质中的传输轨迹是一条直线，在非均匀介质中的传输轨迹是一条曲直线。

用射线去代表光能量传输路线的方法称为射线光学。

射线光学是忽略光波长的光学，亦即射线理论是光波长趋于零的波动理论。

本章将应用射线光学的基本理论对三层平板波导加以分析，目的是对波导的导波原理和与之相关的某些物理概念为读者给出直观的物理意义和清晰的理解，并为以后运用波动光学理论分析各种结构光波导的模式特性打好基础。

1.1 模式类型我们把波导中所能传输的电磁场型称为波导的模式，在平板波导中存在两种基本模式，一种称为TE 模，另一种称为TM 模。

两种模式用光的电场和磁场的偏振方向来定义比较直观。

选择电场只沿平行于波导界面的方向偏振，此时电场垂直于光的传播方向，是横向的，因而把这种模式称为横电模，英文为Transverse Electric Mode ，取其字头称为TE 模。

选择磁场只沿平行于波导界面的方向偏振，此时磁场垂直于光的传播方向，是横向的，因而把这种模式称为横磁模，英文为Transverse Magnetic Mode ，取其字头称为TM 模。

根据模式的导波性或辐射性，可进一步把模式分为导引模式和辐射模式，前者简称导模，而后者简称辐射模。

现来研究三层平板波导，其横截面和相对介电常数分布如图1-1所示，光沿垂直纸面的z 方向传输，图中b 为波导芯厚度，1、2、3分别为芯层、下包层和上包层的相对介电常数，相应的折射率分别为n1、n2、n3，它们与相对介电常数的关系为211n =ε、222n =ε、233n =ε。

为了分析方便，常令321εεε≥>，或321n n n ≥>。

当上下包层为同一种介质时，32εε=，此时为对称三层波导，当上下包层为两种不同的介质时，32εε≠，此时为非对称三层波导。

令光沿z 方向传输，光在y 方向不受限制。

下面我们对非对称三层波导进行分析，即321εεε>>、321n n n >>。

对于对称三层波导，只要在分析结果中令32n n =即可。

0246810246810ε1ε2ε3bε(x )xyxb上 包 层下 包 层波导芯ε2 = n 22ε1 = n 12ε3 = n 32图1-1 三层平板波导的横截面图及相对介电常数分布， 1 >2 3，当2 =3时为对称三层平板波导，当23时为非对称三层平板波导。

1.1.1 折射定律和全反射光在波导中传输时，从射线的角度来看，要不断地在波导的两个界面上发生反射和折射，如图1-2所示。

反射光的轨迹在芯层中是一个锯齿波。

令入射角为1，在下界面的折射角为2，在上界面的折射角为3。

当入射角1较小时光在上下两个界面上都不发生全反射，此时光在上下两个界面上的折射满足折射定律2211sin sin θθn n = 3311sin sin θθn n = (1.1-1)即有332211sin sin sin θθθn n n == (1.1-2)由式(1.1-1)可得2121sin sin θθn n =3131sin sin θθn n =(1.1-3)因为321n n n >>，由式(1.1-2)可判断出321θθθ<<。

当入射角1增大时，折射角为 2 和3也随之增大。

当3增大到90时，光在上界面上发生全反射。

如果入射角1继续增大，使得2也增大到90时，光在下界面上也要发生全反射。

光发生全反射时的入射角称为临界角。

由式(1.1-3)可得到光在下、上两个界面上发生全反射时的临界角12、13分别为1212arcsinn n =θ1313arcsinn n =θ (1.1-4)因为32n n >，所以1312θθ>。

1.1.2 空间辐射模当入射角较小时，使得光在上下两个界面上都不发生全反射，如图1-2所示。

在这种情况下，光在传输过程中不断地有折射光进入上下包层，即光能量不断地从上下包层中辐射出去，这种模式称为空间辐射模。

因此若产生空间辐射模，入射角1必须满足下述条件13131arcsinn n =<θθ (1.1-5)由上式还可得到311sin n n <θ (1.1-6)我们定义11sin θn N =为模式的有效折射率。

引入有效折射率的概念后，产生空间辐射模的条件又可写为3n N < (1.1-7)令002λπ=k ，称k0为为真空中波数，0真空中光波长，并定义N k 0=β为模式的传播常数，它是波矢k 的z 分量，即β=z k 。

引入传播常数的概念后，上式两端同乘以k0，因此产生空间辐射模的条件又可写为300n k N k <=β (1.1-8)我们把产生空间辐射模的条件合写如下13131arcsinn n =<θθ 311sin n n N <=θ 300n k N k <=β (1.1-9)传播常数的单位通常采用cm-1或mm-1。

246810246810θ2n 3n 2n 1θ1θ3θ1图1-2 空间辐射模1.1.3 衬底辐射模 如果入射角1增大到使光在上界面发生全反射但在下界面还没发生全反射，如图1-3所示。

此时光在传输过程中不断地有折射光进入下包层，即光能量不断地从下包层(有时也为衬底)中辐射出去，这种模式称为衬底辐射模。

因此若产生衬底辐射模，入射角1必须满足下述条件121211313arcsin arcsinn n n n =<<=θθθ (1.1-10)由上式还可把产生衬底辐射模的条件写为2113sin n n N n <=<θ (1.1-11)上式两端同乘以真空中波数k0，产生空间辐射模的条件又可写为20030n k N k n k <=<β (1.1-12)246810246810θ2n 3n 2n 1θ1θ1图1-3 衬底辐射模1.1.4 导模 如果入射角1增大到使光在上下两个界面上都发生全反射时，此时上下包层中不再有折射光，如图1-4所示。

在这种情况下，光能量不再向包层中辐射，光被限制在波导芯中以锯齿波的形式沿z 方向传输，这种模式称为导模。

因此若产生导模，入射角1必须满足下述条件11212arcsinθθ<=n n (1.1-13)由上式还可把产生导模的条件写为1112sin n n N n <=<θ (1.1-14)上式两端同乘以真空中波数k0，产生空间辐射模的条件又可写为10020n k N k n k <=<β (1.1-15)2468100246810n 3n 2n 1θ1θ1图1-4 导模1.1.5 禁区 如果入射角1增大到90，则光将沿z 方向前进，此时导模的有效折射率N = n1，传播常数10n k =β，这是导模最大可能的传播常数。

对于组成波导的各层介质都是线性的情况，N > n1或10n k >β的区域为禁区，代表不存在模式的区域。

1.1.6 表面模对于某些特殊结构的波导，如金属包层波导和非线性波导，会出现其有效折射率大于n1、传播常数大于 k0n1的情况。

这种N > n1或10n k >β的模式称为表面模。

1.2 全反射相移光在波导界面上发生全反射时，入射角大于临界角。

以下界面为例，有11212arcsinθθ<=n n 或0sin 122122<-θn n (1.2-1) 下面我们分别讨论TE 和TM 模由全反射而引起的相移。

1.2.1 TE 模的全反射相移 TE 模的反射系数公式为22112211cos cos cos cos 'θθθθn n n n E E r +-==(1.2-2)式中E 、'E 分别为入射场强和反射场强。

光在下界面发生全反射时，利用式(1.1-1)和(1.2-1)可得()()2112212222112222121222sin 1sin 1sin 1cos θθθθn n n n n -=⎪⎪⎭⎫ ⎝⎛-=-=()212212212sin n n n j -=θ (1.2-3)上式说明发生全反射时折射角2变为虚数。

上式代入式(1.2-2)得到()()21221221112122122111sin cos sin cos 'n n j n n n j n E E r -+--==θθθθ()⎥⎥⎦⎤⎢⎢⎣⎡--=1121221221cos sin arctan2exp θθn n n j()122exp φj -= (1.2-4)上式表明，光在下界面发生全反射时，反射光和入射光之间产生一个相移212，其中()112122122112cos sin arctan22θθφn n n-= (1.2-5)令122γγ=T 133γγ=T (1.2-6a)()2122101Nn k -=γ()122202n Nk -=γ()2123203n N k -=γ (1.2-6b)则有()()110112212102122101cos sin θθγn k n n k N n k =-=-= (1.2-7a)()()2122122102122202sin n n k n N k -=-=θγ (1.2-7b) ()()21231221212323sin n nk n Nk -=-=θγ (1.2-7c)代入式(1.2-5)则有()212112122122112arctan 2arctan2cos sin arctan22T n n n==-=γγθθφ (1.2-8)同理，光在上界面发生全反射时的也要产生一个相移213，其中()313112123122113arctan 2arctan2cos sin arctan22T n n n==-=γγθθφ (1.2-9)1.2.2 TM 模的全反射相移 TM 模的反射系数公式为12211221cos cos cos cos 'θθθθn n n n E E r +-== (1.2-10) 光在下界面发生全反射时，上式(1.2-3)代入式(1.2-10)得到()()212212212112212212212112sin cos sin cos 'n n n n j n n n n n j n E E r -+-+-==θθθθ ()⎥⎥⎦⎤⎢⎢⎣⎡--=11212212212221cos sin arctan 2exp θθn n n n n j ()122exp φj -= (1.2-11) 其中212为光在下界面发生全反射时，反射光和入射光之间产生的相移()1121221221222112cos sin arctan 22θθφn n n n n -= (1.2-12)此时令1222212γγn n T =1233213γγn n T =(1.2-13a)()2122101N n k -=γ ()2122202n N k -=γ ()2123203n N k -=γ (1.2-13b)仍有()()110211221210122101cos sin θθγn k n n k N n k =-=-= (1.2-14a)()()2122122102122202sin n n k n N k -=-=θγ (1.2-14b) ()()21231221212323sin n nk n Nk -=-=θγ (1.2-14c)代入式(1.2-12)则有()21222211121221221222112arctan 2arctan2cos sin arctan 22T n n n n n n n ==-=γγθθφ (1.2-15)同理，光在上界面发生全反射时，反射光和入射光之间也要产生一个相移213，其中()31233211121231221232113arctan 2arctan2cos sin arctan 22T n n n n n n n ==-=γγθθφ (1.2-16)对于TE 和TM 模，T 2、T 3的定义是不同的，参见式(1.2-6a)、(1.2-13a)，因而它们的全反射相移也是不同的。