下载文档原格式
层次分析法判断矩阵求权值以及一致性检验程序层次分析法（Analytic Hierarchy Process，AHP）是一种用于多准则决策的数学模型和方法。
它是由美国管理学家托马斯·L·赛蒙在20世纪70年代提出的。
AHP方法能够帮助决策者在多个准则和多个选择之间进行有效的决策，通过定量和定性的方式来对选择进行评估和比较。
在AHP方法中，决策问题被分解成一个层次结构，其中包含目标层、准则层和选择层。
每个层次都有不同的准则和可能的选择。
决策者需要对每个层次中的准则和选择进行配对比较，从而确定它们之间的重要性和权重。
通过对一系列两两比较的判断矩阵求权值，最终得到每个准则和选择的权重，进而做出最终决策。
下面是一种求解AHP中矩阵权值和进行一致性检验的程序：1. 建立判断矩阵：根据决策问题的结构，建立一个判断矩阵。
判断矩阵的大小是n×n，其中n是比较对象的数量。
矩阵的每个元素(a_ij)表示第i个对象相对于第j个对象的重要性或影响程度。
2. 进行两两比较：对矩阵的每个元素(a_ij)，决策者需要进行两两比较，确定它们之间的相对重要性。
比较的结果可以使用系数1-9进行量化，其中1表示相等重要性，9表示绝对重要性的差异。
3.归一化判断矩阵：将比较得到的判断矩阵归一化，使得每一列的元素之和等于1、这可以通过将每个元素除以其所在列的元素之和来实现。
4.求解权值：通过归一化后的判断矩阵，可以计算每个对象的权重。
权重可以通过计算每一行的元素之和来得到。
5.计算一致性指标：在AHP方法中，一致性是指判断矩阵中的数值是否在合理范围内。
为了检验一致性，需要计算一致性指标。
一致性指标的计算方法是通过求解最大特征值和一致性比率来得到。
6.进行一致性检验：计算一致性指标后，需要将其与预先给定的随机一致性指标进行比较。
如果计算得到的一致性指标小于预先给定的一致性指标，则认为判断矩阵中的数值具有一致性。
层次分析法步骤及案例分析层次分析法（AHP）是一种通过对比判断不同因素的重要性来进行决策的方法。
它由匹兹堡大学的数学家托马斯·萨蒙在20世纪70年代初提出，并逐渐应用于各个领域。
本文将介绍层次分析法的步骤，并通过一个实际案例来进行分析。
一、层次分析法的步骤层次分析法主要包括以下几个步骤：1. 确定层次结构：首先，需要明确决策问题的层次结构。
将问题划分为若干个层次，从总目标到具体的子目标，形成一棵树状结构。
例如，在一个购车的决策问题中，总目标可以是“选择一辆适合自己的车”，下面的子目标可以包括“价格”、“外观”、“安全性”等因素。
2. 构造判断矩阵：在每个层次中，需要对不同因素之间的两两比较进行判断。
判断可以基于专家经验、问卷调查或实际数据。
对于两两比较，通常采用一个1到9的比较尺度，其中1表示相等，3表示略微重要，5表示中等重要，7表示强烈重要，9表示绝对重要。
如果因素A相对于因素B的重要性大于1，则B相对于A的重要性是1/A。
3. 计算权重向量：根据判断矩阵中的比较结果，可以计算出每个层次中各个因素的权重向量。
通过对判断矩阵的特征值和特征向量进行计算，可以得到各个因素的权重。
4. 一致性检验：在进行层次分析时，需要检验判断矩阵的一致性。
一致性是指在两两比较中的逻辑关系的一致性。
通常使用一致性指数和一致性比率来判断判断矩阵的一致性程度。
5. 综合评价：通过将各层次中因素的权重向量进行乘积运算，并将结果汇总得到最后的评价结果。
在这一步骤中，可以对不同的决策方案进行排序或进行多目标决策。
二、案例分析为了更好地了解层次分析法的应用，我们来看一个实际案例。
假设某公司需要选择新的供应商，供应商选择的主要考虑因素包括产品质量、交货周期和价格。
我们可以按照以下步骤进行决策：1. 确定层次结构：总目标是选择合适的供应商，下面的子目标是产品质量、交货周期和价格。
2. 构造判断矩阵：对于每个子目标，可以进行两两比较。
function [w,CR]=mycom(A,m,RI)[x,lumda]=eig(A);r=abs(sum(lumda));n=find(r==max(r));max_lumda_A=lumda(n,n);max_x_A=x(:,n);w=A/sum(A);CR=(max_lumda_A-m)/(m-1)/RI;end本matlab程序用于层次分析法中计算判断矩阵给出的权值已经进行一致性检验。
其中A为判断矩阵，不同的标度和评定A将不同。
m为A的维数RI为判断矩阵的平均随机一致性指标：根据m的不同值不同。
当CR<0.1时符合一致性检验，判断矩阵构造合理。
下面是层次分析法的简介，以及判断矩阵构造方法。
一.层次分析法的含义层次分析法（The analytic hierarchy process）简称AHP，在20世纪70年代中期由美国运筹学家托马斯·塞蒂（T.L.Saaty）正式提出。
它是一种定性和定量相结合的、系统化、层次化的分析方法。
由于它在处理复杂的决策问题上的实用性和有效性，很快在世界范围得到重视。
它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。
二.层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一样的。
（1）层次分析法的原理层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构，然后得用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再加权和的方法递阶归并各备择方案对总目标的最终权重，此最终权重最大者即为最优方案。
这里所谓“优先权重”是一种相对的量度，它表明各备择方案在某一特点的评价准则或子目标，标下优越程度的相对量度，以及各子目标对上一层目标而言重要程度的相对量度。
层次分析法比较适合于具有分层交错评价指标的目标系统，而且目标值又难于定量描述的决策问题。
层次分析法实验报告层次分析法实验报告一、引言层次分析法（Analytic Hierarchy Process，简称AHP）是一种多准则决策方法，由美国运筹学家托马斯·L·塞蒂（Thomas L. Saaty）于1970年提出。
该方法通过对决策问题进行层次结构分解，建立判断矩阵，计算权重，最终得出决策结果。
本实验旨在通过使用层次分析法解决一个实际问题，验证该方法在决策问题中的应用效果。
二、实验目的1. 了解层次分析法的基本原理和步骤；2. 掌握构建层次结构和判断矩阵的方法；3. 熟悉计算权重和一致性检验的过程；4. 验证层次分析法在决策问题中的实际应用效果。
三、实验过程1. 确定决策问题：选择一个实际的决策问题，例如购买一台新电脑；2. 构建层次结构：将决策问题分解为准则层、子准则层和方案层，形成层次结构；3. 制作判断矩阵：对每个层次的元素进行两两比较，根据重要性进行评分，构建判断矩阵；4. 计算权重：通过特征向量法计算每个层次的权重；5. 一致性检验：计算一致性指标，判断判断矩阵是否合理；6. 决策结果：根据权重计算得出最终的决策结果。
四、实验结果在购买新电脑的决策问题中，我们构建了准则层、子准则层和方案层的层次结构。
准则层包括性能、价格和品牌三个元素；子准则层包括CPU、内存、硬盘、显卡和屏幕五个元素；方案层包括若干个不同品牌和型号的电脑。
通过对每个层次的元素进行两两比较，我们制作了判断矩阵。
以性能为例，我们对CPU、内存、硬盘、显卡和屏幕进行了两两比较，根据其重要性进行评分。
同样地，我们对价格和品牌也进行了两两比较，得到了相应的判断矩阵。
接下来，我们通过特征向量法计算了每个层次的权重。
将判断矩阵的列向量归一化后，求得特征向量，并计算了每个元素的权重。
通过一致性检验，我们发现判断矩阵的一致性指标在合理范围内，说明判断矩阵的构建是可靠的。
最终，根据权重计算得出了最佳决策结果。
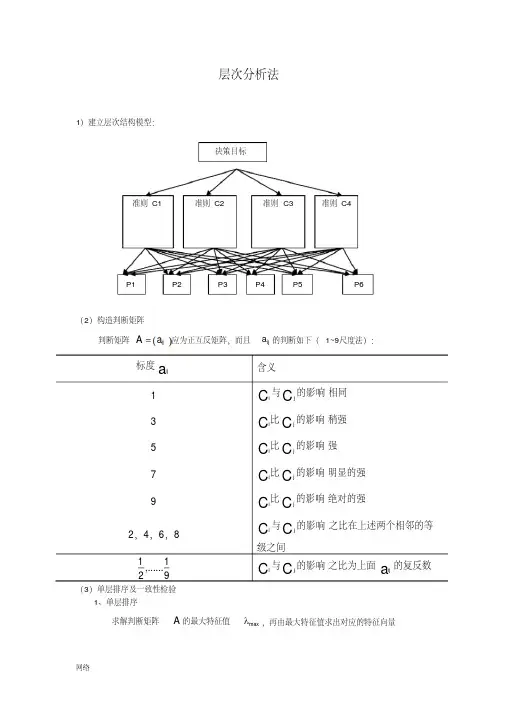
层次分析法1）建立层次结构模型：（2）构造判断矩阵判断矩阵()ij A a =应为正互反矩阵，而且ij a 的判断如下（1~9尺度法）：（3）单层排序及一致性检验1、单层排序求解判断矩阵A 的最大特征值max λ，再由最大特征值求出对应的特征向量ω()max A ωλω=，并将ω标准化，即为同一层相对于上一层某一因素的权重，根据此权重的大小，便可确定该层因素的排序。
2、一致性检验取一致性指标max 1nCI n λ-=-，（n 为A 的阶数）令CICR RI=，若0.1CR <，则认为A 具有一致性。
否则，需要对A 进行调整，直到具有满意的一致性为止。
（4）层次总排序及一致性检验假定准则层12,,,n C C C 排序完成，其权重分别为12,,,n a a a ，方案层P 包含m 个方案：12,,,m P P P 。
其相对于上一层的()1,2,,j C j n =对方案层P 中的m 个方案进行单层排序，其排序权重记为12,,,j j mj b b b()1,2,,j n =，则方案层P 中第i 个方案Pi 的总排序权重为1nj ij j a b =∑，见下表：从而确定层的排序。
例：纯文本文件txt3.txt 中的数据格式如下：1 1 1 4 1 1/2 1 1 2 4 1 1/2 1 1/2 1 53 1/2 1/4 1/4 1/5 1 1/3 1/3 1 1 1/3 3 1 1 2 2 2 3 3 1 1 1/4 1/2 4 1 3 2 1/3 1 1 1/4 1/5 4 1 1/2 5 2 1 1 3 1/3 1/3 1 1/7 3 7 1 1 1/3 5 3 1 7 1/5 1/7 1 1 1 7 1 1 7 1/7 1/7 1 1 7 9 1/7 1 1 1/9 1 1 matlab 程序：>> fid=fopen('txt3.txt','r');n1=6;n2=3;a=[];for i=1:n1tmp=str2num(fgetl(fid));a=[a;tmp]; %读准则层判断矩阵endfor i=1:n1str1=char(['b',int2str(i),'=[];']);str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']); eval(str1);for j=1:n2tmp=str2num(fgetl(fid));eval(str2); %读方案层的判断矩阵endendri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标[x,y]=eig(a);lamda=max(diag(y));num=find(diag(y)==lamda);w0=x(:,num)/sum(x(:,num));cr0=(lamda-n1)/(n1-1)/ri(n1)for i=1:n1[x,y]=eig(eval(char(['b',int2str(i)])));lamda=max(diag(y));num=find(diag(y)==lamda);w1(:,i)=x(:,num)/sum(x(:,num));cr1(i)=(lamda-n2)/(n2-1)/ri(n2);endcr1, ts=w1*w0, cr=cr1*w0。
先确定判断矩阵；
然后用以下程序就好了：
%层次分析法的matlab程序%%%%diertimoxingyi
clc,clear
disp('输入判断矩阵');% 在屏幕显示这句话
A=input('A=');% 从屏幕接收判断矩阵
[n,n]=size(A);% 计算A的维度，这里是方阵，这么写不太好
x=ones(n,100);% x为n行100列全1的矩阵
y=ones(n,100);% y同x
m=zeros(1,100);% m为1行100列全0的向量
m(1)=max(x(:,1));% x第一列中最大的值赋给m的第一个分量
y(:,1)=x(:,1);% x的第一列赋予y的第一列
x(:,2)=A*y(:,1);% x的第二列为矩阵A*y(:,1)
m(2)=max(x(:,2));% x第二列中最大的值赋给m的第二个分量
y(:,2)=x(:,2)/m(2);% x的第二列除以m(2)后赋给y的第二列
p=0.0001;i=2;k=abs(m(2)-m(1));% 初始化p，i，k为m(2)-m(1)的绝对值
while k>p% 当k>p是执行循环体
i=i+1;% i自加1
x(:,i)=A*y(:,i-1);% x的第i列等于A*y的第i-1列
m(i)=max(x(:,i));% m的第i个分量等于x第i列中最大的值
y(:,i)=x(:,i)/m(i);% y的第i列等于x的第i列除以m的第i个分量
k=abs(m(i)-m(i-1));% k等于m(i)-m(i-1)的绝对值
end
a=sum(y(:,i));% y的第i列的和赋予a
w=y(:,i)/a;% y的第i列除以a
t=m(i);% m的第i个分量赋给t
disp('权向量:');disp(w);% 显示权向量w
disp('最大特征值:');disp(t);% 显示最大特征值t
%以下是一致性检验
CI=(t-n)/(n-1);% t-维度再除以维度-1的值赋给CI
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];% 计算的标准
CR=CI/RI(n);% 计算一致性
if CR<0.10
disp('此矩阵的一致性可以接受!');
disp('CI=');disp(CI);
disp('CR=');disp(CR);
else
disp('此矩阵的一致性不可以接受!'); end。
