固体电子学(6,7,8章习题)f

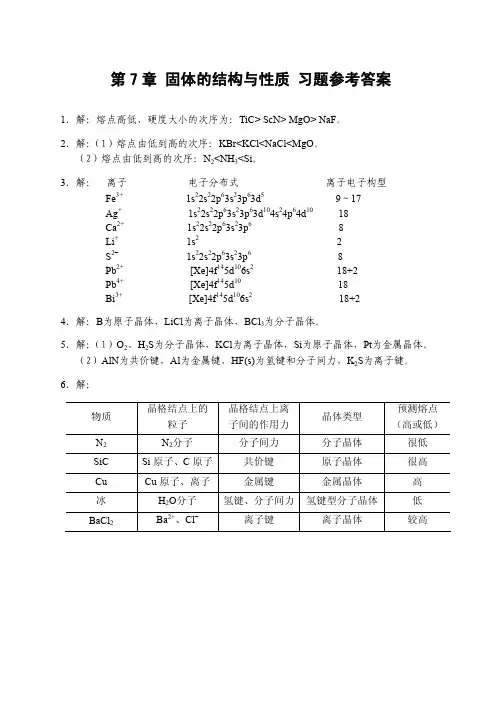
第7章 固体的结构与性质 习题参考答案1．解：熔点高低、硬度大小的次序为：TiC> ScN> MgO> NaF。

2．解：（1）熔点由低到高的次序：KBr<KCl<NaCl<MgO。

（2）熔点由低到高的次序：N2<NH3<Si。

3．解： 离子 电子分布式 离子电子构型 Fe3+ 1s22s22p63s23p63d59～17Ag+1s22s22p63s23p63d104s24p64d1018Ca2+ 1s22s22p63s23p68Li+ 1s2 2S2−1s22s22p63s23p68Pb2+[Xe]4f145d106s2 18+2Pb4+[Xe]4f145d1018Bi3+[Xe]4f145d106s218+24．解：B为原子晶体，LiCl为离子晶体，BCl3为分子晶体。

5．解：（1）O2、H2S为分子晶体，KCl为离子晶体，Si为原子晶体，Pt为金属晶体。

（2）AlN为共价键，Al为金属键，HF(s)为氢键和分子间力，K2S为离子键。

6．解：物质晶格结点上的粒子晶格结点上离子间的作用力晶体类型预测熔点（高或低）N2N2分子分子间力分子晶体很低SiC Si原子、C原子共价键原子晶体很高Cu Cu原子、离子金属键金属晶体高冰H2O分子氢键、分子间力氢键型分子晶体低BaCl2Ba2+、Cl−离子键离子晶体较高7．解： 3θmf Al(s)+ F (g)AlF (s)H Δ⎯⎯⎯→\D (F －F) −UA 13+3e 3F(g)3F (g)E−−⎯⎯⎯→ +\m sub H ΔAl(g) Al 3+(g)U ＝+(F －F)+3+ I − \m sub H Δ\D 1AE \m f H Δ＝ [326.4+32×156.9+3×（−322）+5139.1−（−1510）]kJ · mol −1＝ 6245 kJ · mol −18．解：f mH ΔK(s) +12I 2(s)KI(s)sub m H Δ(K) sub m H Δ(I 2)12I 2(g) −U12θ(I-I)D I(g) +e − I −(g)+ 1A E −e −K(g) I 1 K +(g)Δ=(K)+ \m f H \m sub H Δ12\m sub H Δ(I 2)+ 12θ(I-I)D ++ I 1A E 1 −U=[90+ 12×62.4+12×152.549+(−295)+418.9−649] kJ · mol −1=−328 kJ · mol −19．解：（1）极化力：Na +，，Al 3+，Si 4+；变形性：Si 4+，Al 3+，Na +。

第四章 固体电子论 参考答案1. 导出二维自由电子气的能态密度。

解：二维情形，自由电子的能量是：2πL x x k n =，2πL y y k n =在/k =h 到d k k +区间： 那么：2d ()d Z Sg E E =其中：22()πm g E =h2. 若二维电子气的面密度为n s ，证明它的化学势为：解：由前一题已经求得能态密度：电子气体的化学势μ由下式决定： ()()222E-/E-/001d ()d πe 1e 1B B k T k T L m E N g E L E μμ∞∞==++⎰⎰h 令()/B E k T x μ-≡，并注意到：2s N n L=那么可以求出μ：证毕。

3. He 3是费米子，液体He 3在绝对零度附近的密度为0.081 g ／cm 3。

计算它的费米能E F 和费米温度T F 。

解：He 3的数密度：其中m 是单个He 3粒子的质量。

可得：代入数据，可以算得： E F ＝6.8x 10-16 erg = 4.3x 10-4eV.则：F F E T k =＝4.97 K.4.已知银的密度为310.5/g cm ，当温度从绝对零度升到室温（300K ）时，银金属中电子的费米能变化多少？解：银的原子量为108，密度为310.5/g cm ，如果1个银原子贡献一个自由电子，1摩尔物质包含有6.022x 1023个原子，则单位体积内银的自由电子数为在T=0K 时，费米能量为代如相关数据得2/3272227302812(6.6310)()3 5.910()29.110()8 3.148.8710() 5.54()F erg s cm E g erg eV -----⎛⎫⨯⋅⨯⨯= ⎪⨯⨯⨯⎝⎭≈⨯≈ 在≠T 0K 时，费米能量所以，当温度从绝对零度升到室温（300K ）时, 费米能变化为代如相关数据得可见，温度改变时，费米能量的改变是微不足道的。

5. 已知锂的密度为30.534/g cm ，德拜温度为370K ，试求（1）室温（300K ）下电子的摩尔比热；（2）在什么温度下，锂的电子比热等于其晶格比热？解：（1）金属中每个电子在常温下贡献的比热 2'0()2B V B F k T C k E π= （1） 式中0FE 为绝对零度下的费米能： 202/33()28F h n E m π= （2）锂的密度30.534/g cm ，原子量6.94，每立方厘米锂包含的摩尔数为0.534/6.94，1摩尔物质中包含 6.022x 1023个原子，每个锂贡献一个电子，则每立方厘米中的电子数已知将数据代入（2）得在室温（300K ）下，0.026B k T eV =，由（1）式可以求得电子的摩尔比热代入相关数据得（2）电子比热只在低温下才是重要的。

第一章 金属自由电子气体模型习题及答案1. 你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的？[解答] 自由电子论只考虑电子的动能。

在绝对零度时，金属中的自由（价）电子，分布在费米能级及其以下的能级上，即分布在一个费米球内。

在常温下，费米球内部离费米面远的状态全被电子占据，这些电子从格波获取的能量不足以使其跃迁到费米面附近或以外的空状态上，能够发生能态跃迁的仅是费米面附近的少数电子,而绝大多数电子的能态不会改变。

也就是说，常温下电子的平均动能与绝对零度时的平均动能十分相近。

2. 晶体膨胀时，费米能级如何变化？[解答] 费米能级3/222)3(2πn mE o F= ， 其中n 单位体积内的价电子数目。

晶体膨胀时，体积变大，电子数目不变，n 变小，费密能级降低。

3． 为什么温度升高，费米能反而降低？[解答] 当K T 0≠时，有一半量子态被电子所占据的能级即是费米能级。

除了晶体膨胀引起费米能级降低外，温度升高，费米面附近的电子从格波获取的能量就越大，跃迁到费米面以外的电子就越多，原来有一半量子态被电子所占据的能级上的电子就少于一半，有一半量子态被电子所占据的能级必定降低，也就是说，温度生高，费米能反而降低。

4． 为什么价电子的浓度越大，价电子的平均动能就越大？[解答] 由于绝对零度时和常温下电子的平均动能十分相近，我们讨论绝对零度时电子的平均动能与电子的浓度的关系。

价电子的浓度越大，价电子的平均动能就越大，这是金属中的价电子遵从费米—狄拉克统计分布的必然结果。

在绝对零度时，电子不可能都处于最低能级上，而是在费米球中均匀分布。

由式3/120)3(πn k F =可知，价电子的浓度越大费米球的半径就越大，高能量的电子就越多，价电子的平均动能就越大。

这一点从3/2220)3(2πn m E F=和3/222)3(10353πn mE E oF ==式看得更清楚。

电子的平均动能E 正比于费米能o F E ，而费米能又正比于电子浓度32l n。

固体物理期末考试题及答案一、选择题（每题2分，共20分）1. 晶体中原子排列的周期性结构被称为：A. 晶格B. 晶胞C. 晶面D. 晶向答案：A2. 描述固体中电子行为的基本理论是：A. 经典力学B. 量子力学C. 相对论D. 电磁学答案：B3. 以下哪项不是固体物理中的晶体缺陷：A. 点缺陷B. 线缺陷C. 面缺陷D. 体缺陷答案：D4. 固体物理中，晶格振动的量子称为：A. 声子B. 光子C. 电子D. 空穴答案：A5. 以下哪个不是固体的电子能带结构：A. 价带B. 导带C. 禁带D. 散射带答案：D二、简答题（每题10分，共30分）6. 解释什么是晶格常数，并举例说明。

晶格常数是晶体中最小重复单元的尺寸，通常用来描述晶体的周期性结构。

例如，立方晶系的晶格常数a是指立方体的边长。

7. 简述能带理论的基本概念。

能带理论是量子力学在固体物理中的应用，它描述了固体中电子的能量分布。

在固体中，电子的能量不是连续的，而是分成一系列的能带。

价带是电子能量较低的区域，导带是电子能量较高的区域，而禁带是两带之间的能量区域，电子不能存在。

8. 什么是费米能级，它在固体物理中有什么意义？费米能级是固体中电子的最高占据能级，它与温度有关，但与电子的化学势相等。

在绝对零度时，费米能级位于导带的底部，它决定了固体的导电性质。

三、计算题（每题15分，共30分）9. 假设一个一维单原子链的原子质量为m，相邻原子之间的弹簧常数为k。

求该链的声子频率。

解：一维单原子链的声子频率可以通过下面的公式计算：\[ \omega = 2 \sqrt{\frac{k}{m}} \]10. 给定一个半导体的电子亲和能为Ea，工作温度为T，求该半导体在该温度下的费米-狄拉克分布函数。

解：费米-狄拉克分布函数定义为：\[ f(E) = \frac{1}{e^{\frac{E-E_F}{kT}} + 1} \] 其中，E是电子的能量，E_F是费米能级，k是玻尔兹曼常数，T 是温度。

固体物理习题一、 固体电子论基础1． 已知金属铯的E F =1.55eV ，求每立方厘米的铯晶体中所含的平均电子数。

(提示:常温下F E 与0F E 相差不大，可以令0F F E E ≈)解：因为常温下费米能级E F 与绝对零度时的费米能级E F 0相差不大，可令E F ≈E F 0。

金属中的电子可近似地按自由电子气处理，在E ～E+dE 能量区间内的电子态数(计及自旋)为:()dE CE dE E hm VdZ 212132324==π其中：()2132324E hm VC π=， V 为金属的体积，m 为电子的质量。

由于电子遵循费米分布，于是在能量区间E ～E+dE 中的电子数为： dE E E Cf dZ E f dN )()(==式中)(E f 是费米分布函数。

由于在绝对零度时有：⎪⎩⎪⎨⎧><=)E (E 0)E (E 1)(0F 0FE f因此电子总数为：2332300)2(38)(32)(0F FE mE h VE C dEE C dE E E Cf N Fπ====⎰⎰∞单位体积内的电子数为： 233)2(38F mE hV Nn π==代入有关数据得到： )(108.7 )106.155.1101.92()1063.6(314.38321231228327----⨯≈⨯⨯⨯⨯⨯⨯⨯⨯⨯=cm n2． 证明：在T=0K 时，费米能级0F E 处的能态密度为：0023)(FF EN E N =，式中N为金属中的自由电子数。

证明：在K 空间中，在周期性边界条件下，以K K =为半径的球内，电子的数目为（记及自旋）：3342K V n π⋅=因此：dK K V dn 28π⋅= （1） 已知自由电子的能量为：mK h E 222=，代入（1）式得：d E E hm Vd n 21323)2(4π= （2）因此电子按照能量分布的状态密度：21323)2(4)(E hm Vd E d nE N π==（3）当T=0K 时，全部电子处于费米球内。

福州大学至诚学院《固体电子学》试卷答案（一）一、单项选择（每题 2 分，共10 分）1．电子在晶体中的共有化运动指的是 C 。

A．电子在晶体中各处出现的几率相同B．电于在晶体原胞中各点出现的几率相同C. 电子在晶体各原胞对应点出现的几率相同D．电子在晶体各原胞对应点有相同位相2．离子晶体可能的最大配位数是 B 。

A．12 B．8 C．6 D．43．根据费米分布函数，电子占据（E F + kT）能级的几率 B 。

A．等于空穴占据（E F + kT）能级的几率 B. 等于空穴占据（E F－kT）能级的几率C．大于电子占据E F的几率D．大于空穴占据E F的几率4．下列说法中错误的是 A 。

A．特鲁德模型，即量子的自由电子气模型，是建立在金属电子气体假设基础上的。

B. 在特鲁德模型中，认为金属电子气体是玻色子，遵循玻尔兹曼统计规律。

C．在索末菲模型中，认为金属电子气体是费米子，遵循费米统计规律。

D. 特鲁德对金属结构的基本描述是金属原子由原子实和价电子两部分构成。

5．对于只含一种杂质的非简并n型半导体，费米能级E F随温度上升而 D 。

A．单调上升 B. 单调下降C．经过一极小值趋近E F D．经过一极大值趋近E F二、填空（每空 2 分，共20 分）1．氯化钠结构复式格子可以看作是由两个面心立方结构子晶格套构而成。

2．电子亲和能一般随着原子半径的减小而增大。

3．由正负离子相间排列的一维离子链的马德隆常数是2ln2 。

4．B原子在Si晶体中形成的是p型半导体，P原子在Si晶体中形成的是n型半导体。

5．原子电负性=0.18（电离能+ 电子亲和能），用它来作为一种元素的原子对外层电子吸引能力的衡量尺度。

6．两种不同金属接触后，费米能级高的金属带正电，对导电有贡献的是费米面附近位置的电子。

7．我们一般采用回旋共振实验来测量有效质量。

三、简答题（每题8分，共24分）1．从能带论的角度解释为什么导体，半导体和绝缘体的导电能力存在差别；半导体与导体，半导体与绝缘体的最大区别在哪里？答：满带和空带不导电，半满带才导电。

固体物理学考试题及答案一、选择题（每题2分，共20分）1. 固体物理学中，描述晶体中原子排列的周期性规律的数学表达式是（）。

A. 布洛赫定理B. 薛定谔方程C. 泡利不相容原理D. 费米-狄拉克统计答案：A2. 固体中电子的能带结构是由（）决定的。

A. 原子的核外电子B. 晶体的周期性势场C. 原子的核电荷D. 原子的电子云答案：B3. 在固体物理学中，金属导电的原因是（）。

A. 金属中存在自由电子B. 金属原子的电子云重叠C. 金属原子的价电子可以自由移动D. 金属原子的电子云完全重叠答案：C4. 半导体材料的导电性介于导体和绝缘体之间，这是因为（）。

A. 半导体材料中没有自由电子B. 半导体材料的能带结构中存在带隙C. 半导体材料的原子排列无序D. 半导体材料的电子云完全重叠答案：B5. 固体物理学中，描述固体中电子的波动性的数学表达式是（）。

A. 薛定谔方程B. 麦克斯韦方程C. 牛顿第二定律D. 热力学第一定律答案：A6. 固体中声子的概念是由（）提出的。

A. 爱因斯坦B. 德拜C. 玻尔D. 费米答案：B7. 固体中电子的费米能级是指（）。

A. 电子在固体中的最大能量B. 电子在固体中的最小能量C. 电子在固体中的平均水平能量D. 电子在固体中的动能答案：A8. 固体物理学中，描述固体中电子的分布的统计规律是（）。

A. 麦克斯韦-玻尔兹曼统计B. 费米-狄拉克统计C. 玻色-爱因斯坦统计D. 高斯统计答案：B9. 固体中电子的能带理论是由（）提出的。

A. 薛定谔B. 泡利C. 费米D. 索末菲答案：D10. 固体中电子的跃迁导致（）的发射或吸收。

A. 光子B. 声子C. 电子D. 质子答案：A二、填空题（每题2分，共20分）1. 固体物理学中，晶体的周期性势场是由原子的______产生的。

答案：周期性排列2. 固体中电子的能带结构中，导带和价带之间的能量区域称为______。

答案：带隙3. 金属导电的原因是金属原子的价电子可以______。