电工电子学第2章习题解答

第2章正弦交流电路习题解答习2.1题π⎞⎛电流i = 10sin ⎜100πt −⎟，问它的三要素各为多少？在交流电路中，有两个负载，3⎠⎝π⎞π⎞⎛⎛已知它们的电压分别为u1 = 60sin ⎜ 314t −⎟ V，u2 = 80sin ⎜ 314t + ⎟ V，求总电压u 的瞬时值6⎠ 3⎠⎝⎝表达式，并说明u、u1、u2 三者的相位关系。

解：(1)最大值为10（V），角频率为100 π rad/s，初相角为-60°。

（2）U1m = 60 / − 30°（V）U 2 m = 80 / 60°（V）则U m = U1m + U 2 m = 60 / −30° + 80 / 60°= 100 / 23.1°（V）u = 100 sin(314t + 23.1°) （V）u 滞后u2，而超前u1。

2.2两个频率相同的正弦交流电流，它们的有效值是I1=8A，I2=6A，求在下面各种情况下，合成电流的有效值。

（1）i1 与i2 同相。

（2）i1 与i2 反相。

（3）i1 超前i2 90º角度。

（4）i1 滞后i2 60º角度。

解：1）I = I1 + I 2 = 8 + 6 = 14 （A）（（2）I= I 1 − I 2 = 8 + 6 （A）I1 + I 2 = 82 + 62 = 10 （A）2 2（3）I =（4）设I1 = 8/ 0°（A）则I 2 = 6 / 60°（A）I = I1 + I 2 = 8/ 0° + 6/ 60° = 12.2/ 25.3°（A）I = 12.2 （A）2.3 把下列正弦量的时间函数用相量表示。

（1）u = 10 2 sin314t V 解：(1) U =10/0º (V) （2）i = −5 sin(314t –60º) A (2) I m =－5/－60º =5/180º－60º=5/120º (A)2.4 已知工频正弦电压uab 的最大值为311V，初相位为–60°，其有效值为多少？写出其瞬时值表达式；当t=0.0025s 时，Uab 的值为多少？解：∵U abm = 2 U ab∴有效值U ab =1 1 × 311 = 220 (V) U abm =2 2 瞬时值表达式为u ab = 311sin (314t −60°) (V) ⎛⎝当t=0.0025S 时，U ab = 311 × sin ⎜100π×0.0025 −π⎞⎟= 311sin( − ) = −80.5 (V) 3⎠ 12π2.5题 2.5 图所示正弦交流电路，已知u1=220 2 sin314t V，u2=220 2 sin(314t–120º) V，第2章正弦交流电路习题解答65试用相量表示法求电压ua 和ub。

一、选择题1、如图所示，其节点数、支路数、回路数及网孔数分别为（C ）。

A、2、5、3、3B、3、6、4、6C、2、4、6、32、如图所示，I=（B ）A。

A、2B、7C、5D、63、如图所示，E=（B ）V。

A、3B、4C、—4D、—3/4、如图所示电路中，I1和I2的关系为（C ）。

A、I1<I2B、I1>I2C、I1=I2D、不确定5、如图所示，求I1和I2的大小。

解：对于左边节点：I1=10+3+5=18A对于右边节点：I2=10+2-5=7A6、基尔霍夫第一定律的依据是（D ）A.欧姆定律B.全电流定律C.法拉第定律D.电荷守恒定￥7、理想电压源和理想电流源间（C ）A.有等效变换关系B.没有等效变换关系C.有条件下的等效关系D.无法判定8、下列说法错误的是（D ）A.在电路节点处，各支路电流参考方向可以任意设定。

B.基尔霍夫电流定律可以扩展应用于任意假定的封闭面。

C.基尔霍夫电压定律应用于任意闭合路径。

D.∑I=0式中各电流的正负号与事先任意假定的各支路电流方向无关9、实际电压源和电流源模型中，其内阻与理想电压源和电流源之间的正确连接关系是（C）A.理想电压源与内阻串联，理想电流源与内阻串联"B.理想电压源与内阻并联，理想电流源与内阻串联C.理想电压源与内阻串联，理想电流源与内阻并联D.理想电压源与内阻并联，理想电流源与内阻并联10、79.下面的叙述正确的是（B ）。

A.理想电压源和理想电流源是不能等效变换的B.理想电压源和理想电流源等效变换后内部是不等效的C.理想电压源和理想电流源等效变换后外部是不等效的D.以上说法都不正确二、填空题1、不能用电阻串、并联化简的电路称为__复杂电路_______。

;2、电路中的_____每一分支_______称为支路，____3条或3条以上支路___所汇成的交点称为节点，电路中__________闭合的电路______________都称为回路。

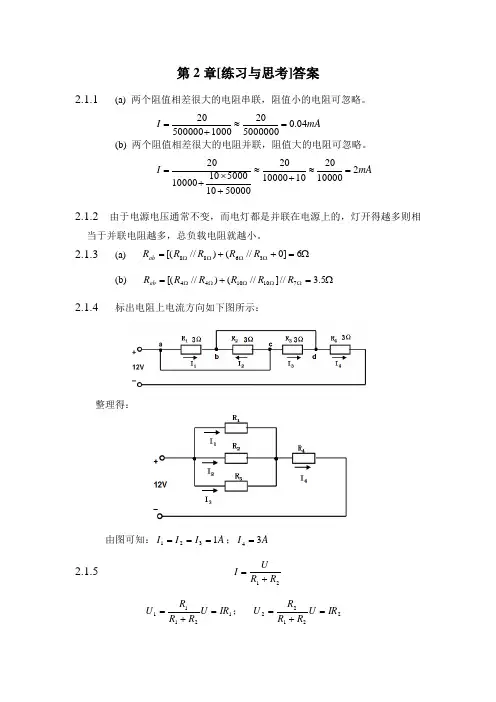
第2章[练习与思考]答案2.1.1 (a) 两个阻值相差很大的电阻串联，阻值小的电阻可忽略。

mA I 04.0500000020100050000020=≈+=(b) 两个阻值相差很大的电阻并联，阻值大的电阻可忽略。

mA I 2100002010100002050000105000101000020=≈+≈+⨯+=2.1.2 由于电源电压通常不变，而电灯都是并联在电源上的，灯开得越多则相当于并联电阻越多，总负载电阻就越小。

2.1.3 (a) Ω=++=ΩΩΩΩ6]0//()//[(3688R R R R R ab(b) Ω=+=ΩΩΩΩΩ5.3//]//()//[(7101044R R R R R R ab2.1.4 标出电阻上电流方向如下图所示：整理得：由图可知：A I I I 1321===；A I 34=2.1.5 21R R UI +=12111IR U R R R U =+=； 22122IR U R R R U =+=(1) Ω=k R 302时， mA I 5.0301020=+=V IR U 511== ； V IR U 1522== (2) ∞→2R 时， 0=I ；01=U ； 02=U (3) Ω=k R 02时， mA I 21020==V IR U 2011== ； V IR U 022==在电路通路时，电阻2R 上无电压无电流的情况是电阻2R 被短接，如下图所示：2.1.6 (1) S 断开时：滑动触点在a 点，V U 100= 滑动触点在b 点，V U 00= 滑动触点在c 点，V U R R R U 52120=+=(2) S 闭合时：滑动触点在a 点，V U 100= 滑动触点在b 点，V U 00= 滑动触点在c 点，V U R R R R R U L L44.4////2120=+=2.1.7 U R R R R R R U R R R R R U L P LL L )//()(//////2222120+-=+=故可知： Ω=k R 217.01；Ω=k R 783.022.3.12.3.2 (1) 不是（2）对(a)图有V U U S 122==，A R U I 3412222=== 对(b)图有A I I S 22==，V R I U 8222==(3) 无影响 （4 ）对(a)图有A R R U I S5//21==对(b)图有V R R I U S 20)(21=+=(5) 有影响。

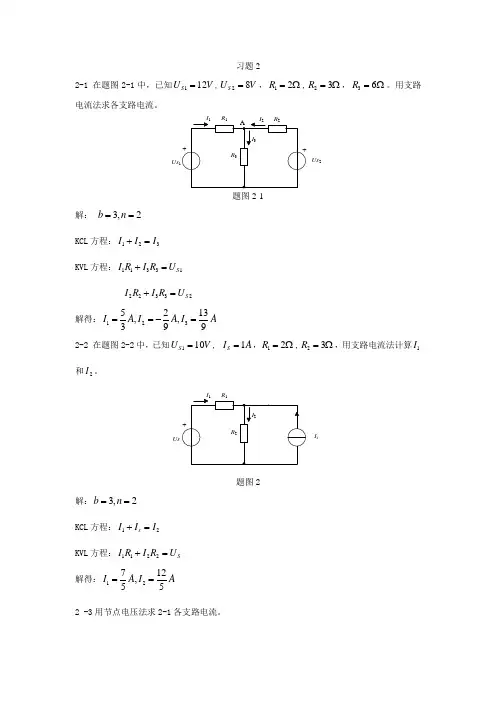
习题22-1 在题图2-1中，已知112S U V =,28S U V =，12R =Ω,23R =Ω，36R =Ω。

用支路电流法求各支路电流。

Us 2Us题图2-1解： 3,2b n == KCL 方程：123I I I += KVL 方程：11331S I R I R U += 22332S I R I R U += 解得：1235213,,399I A I A I A ==-= 2-2 在题图2-2中，已知110S U V =, 1S I A =，12R =Ω,23R =Ω，用支路电流法计算1I 和2I 。

IsUs题图2解：3,2b n == KCL 方程：12s I I I += KVL 方程：1122S I R I R U += 解得：12712,55I A I A ==2 -3用节点电压法求2-1各支路电流。

解：121212312882623611111133236s S abU U R R U V R R R ++===+=++++ 11126125323s abU U I A R --=== 2222682339S abU U I A R --===- 332613369ab U I A R ===2-4用节点电压法求2-2的电流1I 和2I 。

解：112101627.211115236sS abU I R U V R R ++====++111107.21.42s ab U U I A R --=== 227.2 2.43ab U I A R ===或211 1.41 2.4S I I I A =+=+= 2-5 在题图2-5中，已知110s U V =, 26S U V =, 2S I A =,12R =Ω,23R =Ω，36R =Ω，1S R =Ω，用节点电压法求电流1I 和2I 和3I 。

sR U题图2-5解：设上面的节点为a ，下面的节点为b 则12121231262236111111236s S S abU U I R R U V R R R +-+-===++++11112632S ab U U I A R --=== 2226603S ab U U I A R --===33616ab U I A R === 2-6在题图2-6中，已知10S U V =, 2S I A =，14R =Ω,22R =Ω，38R =Ω。

第二章 电路的分析方法2.1.1 在图2.01的电路中，V 6=E ，Ω=61R ，Ω=32R ，Ω=43R ，Ω=34R ，Ω=15R 。

试求3I 和4I 。

4I ↓图2.01解：图2.01电路可依次等效为图（a ）和图（b ）。

R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。

Ω=1R A2S =图2.12解：根据电压源与电流源的等效变换，图2.12所示电路可依次等效为图（a ）和图（b ），由图（b ）可求得A 2.15.023=+=I由图（a ）可求得：A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中，（1）当将开关S 合在a 点时，求电流1I ，2I 和3I ；（2）当将开关S 合在b 点时，利用（1）的结果，用叠加定理计算电流321,I I I 和 。

I图2.19I (a)I (b)解：（1）当将开关S 合在a 点时，图2.19所示电路即为图（a ），用支路电流法可得：=+=+=+12042130423231321I I I I I I I 解得：===A 25A 10A 15321I I I(2)开关S 合在b 点时，利用叠加原理图2.19所示电路可等效为图（a ）和图（b ），其中图（a ）电路中130V 和120V 两个电压源共同作用时所产生的电流已在（1）中求得，即：A 151=,I A 102=,I A 253=,I由图3（b ）可求得：A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则：A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20（a ）所示，V 10ab ,,V 124321=====U R R R R E 。

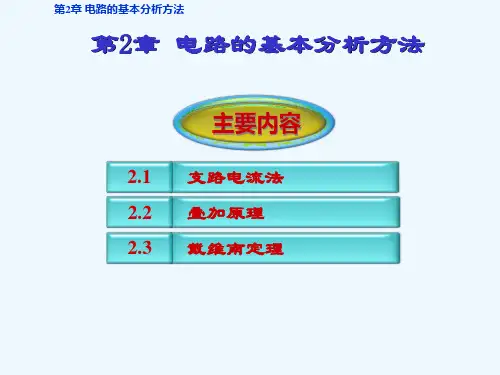
第2章习题参考答案2.1 在题2.1图电路中，1234300R R R R ====Ω，5600R =Ω，试求开关s 断开和闭合时a 和b 之间的等效电阻题2.1图 题2.2图解： 开关S 断开，R 1与R 3串联，R 2与R 4并联，最后它们同R 5并联， 5132411111111600600600200ab R R R R R R =++=++=++，200ab R =Ω 开关S 闭合，R 1与R 2并联，R 3与R 4并联，它们再串联后与R 5并联，20013001600115015016001////11143215=+=++=++=R R R R R R ab Ω=200ab R2.2 在题2.2图电路中，12343,6,12,24R R R R =Ω=Ω=Ω=Ω，试计算等效电阻ab R 。

解： 由于R 1R 4=R 2R 3，所以电桥平衡，R 5支路断开Ω==+=+++=2.7365361911114321ab ab R R R R R R2.3 在题2.3图电路中，计算无源二端电阻网络ab 的等效电阻。

ab题2.3图 题2.4图解：[]Ω=+=+=++=53212//4212//26//32ab R2.4 用等效变换的方法计算题2.4图所示电路中的电流I 、1I 、2I 和电压U 。

解：24K Ω电阻与8K Ω电阻为并联关系，等效电阻1R 为mAU I mA U I VI R U mA I R 5.18/128/,5.024/1224/12,2)612/(366)824/()824(8//242111=========+=KΩ=+⨯==所以 2.5 试计算题2.5图所示电路中5Ω电阻上的电流I ，以及10V 电压源的电流1I 。

题2.5图 题2.6图解：(1)先用等效的方法求I所以原电路中电源部分可等效化简为：3065I A== (2)再回到原电路中求I ：由KCL 得：651==+I I 所以A I 1561=-=2.6 试化简题2.6图所示的有源二端网络。

第2章 习 题 解 答2-1、写出下列各相量所对应的时间函数：（1）12________1072A, 5150A; I I =︒=-︒∠∠ （2）m 2m ________200120V, 30060V U U =︒=-︒∠∠。

解：（1）1272) A, 150) A i t i t ωω=+︒=-︒ （2）2200sin(120) V, 300sin(60) V u t u t ωω=+︒=-︒2-2、试求下列各相量所代表的同频率正弦量之和，并写出它们的时间表达式：（1）1___1.517I =︒∠A ，2____70042 mA;I =-︒∠ （2）1m ____40150I =︒∠ A ，2m ____0.02530 kA I =-︒∠。

解：（1）12 1.5(cos17jsin17) A 0.7[cos(42)jsin(42)] A I I I =+=︒+︒+-︒+-︒ ______(1.954j0.02) A 1.9540.85A =-=-︒∠即 0.85) A i t ω=-︒ （2）m 1m 2m I I I =+ ____________(4015025 150)A 15150A =︒-︒=︒∠∠∠ 即 15sin(150) A i t ω=+︒2-3、设有正弦电流1214.14sin(50) A, 28.3cos(50) A,i t i t ωω=-︒=-︒ 写出它们的最大值和有效值相量表示式，并画出相应的相量图。

解：j501m 1________14.14e A 14.1450A, 1050A I I -︒==-︒=-︒∠∠j(9050)2m 2______28.3e A 28.340A,2040A I I ︒-︒==︒=︒∠∠ 相量图如图2-55所示。

图2-55 题2-3相量图2-4、如图2-41所示，已知1230) A, A,i t i t =-︒= 求i 3和三只电流表的读数（电流表的读数是有效值）。

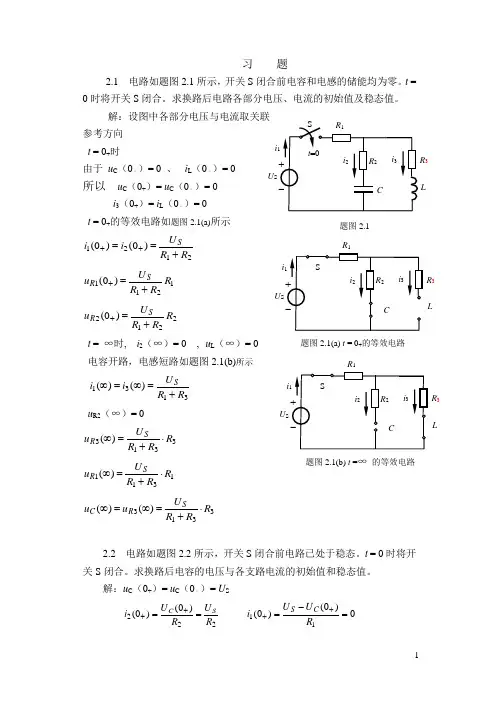
习 题2.1 电路如题图2.1所示，开关S 闭合前电容和电感的储能均为零。

t =0时将开关S 闭合。

求换路后电路各部分电压、电流的初始值及稳态值。

解：设图中各部分电压与电流取关联 参考方向 t = 0+时由于 u C （0–）= 0 、 i L （0–）= 0所以 u C （0+）= u C （0–）= 0i 3（0+）= i L （0–）= 0 t = 0+的等效电路如题图2.1(a)所示2121)0()0(R R U i i S+==++1211)0(R R R U u SR +=+2212)0(R R R U u SR +=+t = ∞时, i 2（∞）= 0 , u L （∞）= 0电容开路，电感短路如题图2.1(b)所示3131)()(R R U i i S+=∞=∞u R2（∞）= 03313)(R R R U u SR ⋅+=∞1311)(R R R U u SR ⋅+=∞3313)()(R R R U u u SR C ⋅+=∞=∞2.2 电路如题图2.2所示，开关S 闭合前电路已处于稳态。

t = 0时将开关S 闭合。

求换路后电容的电压与各支路电流的初始值和稳态值。

解：u C （0+）= u C （0–）= U S222)0()0(R U R U i S C ==++ 0)0()0(11=-=++R U U i C S题图2.1 3 U S Li 题图2.1(a) t = 0的等效电路R 3 U S Li 题图2.1(b) t =∞ 的等效电路R 3 U S Li221)0()0()0(R U i i i S c -=+-+=+稳态0)(=∞c i ，212)(R R R U u Sc +=∞ 2121)()(R R U i i S+=∞=∞2.3 在题图2.3所示电路中，u C （0）= 0，U = 9V ，R = 100k Ω，C = 50μF 。

t = 0时将开关S 闭合。

第2章 习题解答(部分)2.3.3 计算图2.13中的电流 I 3。

解: 用电源等值互换法将电流源变换成电压源，将电阻R 2和R 3合并成电阻R 23，其中 V R I U R S S 2125.043,2=⨯=⨯=Ω=参考方向如图2.34所示。

求电路中电流IA R R R U U I S 2.115.012143,211=+++=+++= I 即为原电路中R 1上流过的电流，用分流公式，可求原电路中I 3A I R R R I 6.02.11113223=⨯+=⨯+= 2.4.1 图2.16是两台发电机并联运行的电路。

已知E 1=230V , R 01=0.5Ω，E 2=226V , R 02=0.3 Ω,负载电阻R L =5.5Ω，试分别用支路电流法和结点电压法求各支路电流 。

解:（1）用支路电流法：各支路电流参考方向已画在图2.16中。

列结点电压方程 L I I I =+21列回路电压方程L L 0222LL 0111R I R I E R I R I E +=+=S Ω 图 2.13 习题2.3.3的图U S U 图解 2.34101202图2.16 习题2.4.1的图联立求解上述三各方程式组成的方程组，可得A 40A2021===L I I I验算：按非独立回路方程进行02201121R I R I E E -=-代入数据443.0205.020226230==⨯-⨯=- （正确！）（2）用结点电压法求解：先求端电压U ，有V 2205.513.015.013.02265.02301110201022011=+++=+++=L R R R R E R E U A 405.0220A 205.0220226A 205.022023002220111====-=-==-=-=L L R U I R U E I R U E I 结果与上相同。

2.5.1 试用结点电压法求图2.18所示电路中的各支路电流解:在原图2.18中用O 和O ’标明两个结点，则有A 5.0505025V 505015015015025501005025a O ,O'-=-==++++=I U A 5.0505025A 15050100c b -=-==-=I I 2.6.1 用叠加原理计算图2.19中各支路的电流。

第二章电路分析基础2-1 电路如图所示，已知US1=24V，US2=16V，IS=1A，R1=R2=8Ω，R3=4Ω。

试用支路电流法求各支路电流。

解：该题有四条支路其中一条支路是恒流源（设恒流源两端电压为U IS），应列四个方程。

有两个节点，按KCL定理可列一个节点方程： I1+I2 =I S+I3有三个网孔按KVL定理可列三个回路方程：I1R1 =U S1+U ISI2R2 =U S2+U IS I2R2+I3R3 =U S2 U IS=I3R3 解之 I1=2A I2=1A I3=2A U S=8V2-2 电路如图所示。

已知I S=2A，U S=6V，R1=R2=3Ω，R3=R4=6Ω，用叠加原理求a、b两点之间电压U ab。

解：当电压源U S单独作用时，题图变如右图：Uab1=当电流源I S单独作用时，题图变如右图Uab2=3V Uab=Uab1+Uab2=2-3 电路如图所示。

已知R1=6Ω，R2=12Ω，R3=8Ω，R4=4Ω，R5=1电路中流经R3的电流I当电流源I S单独作用时，题图变如右图)(13844434AIRRRI=⨯+=+=''I=)(211AII=+=''+'2-4 在图示电路中，当U S=24V时，Uab=8v. 试用叠加原理求U S=0时的UabIs。

解：当电压源U S单独作用时，题图变如右图)(1841243ARRUI S=+=+='解：以知U S=24V时，Uab=8v.当U S、、I S1、I S2、单独作用时题图分别变作变作下图1、图2、图3由图1可得：Uab1=)(64244VRRUS-=-=⨯；由图2可得：Uab2=)(212411VRIRRISS=⨯；由图3可得：Uab3=)(41422VRIRISS=⨯；UabIs=Uab2+Uab3=8+6=14（V）2-5 用电源等效变换法求图示电路中6Ω电阻中的电流I。

第2章习题答案2.1.1 选择题（1）在图2-73所示电路中，发出功率的元件是__Ａ___。

（Ａ）仅是5Ｖ的电源（Ｂ）仅是2Ｖ的电源（Ｃ）仅是电流源（Ｄ）电压源和电流源都发出功率（Ｅ）条件不足图2-73题2.1.1（1）图图2-74题2.1.1（2）图（2）在图2-74所示电路中，当增大时，恒流源两端的电压Ｕ__B___。

（A）不变（B）升高（C）降低（3）在图2-75所示电路中，当开关S闭合后，P点的电位__B___。

（A）不变（B）升高（C）为零（4）在图2-76所示电路中，对负载电阻R而言，点画线框中的电路可用一个等效电源代替，该等效电源是__C___。

（A）理想电压源（B）理想电流源（C）不能确定图2-75题2.1.1（3）图图2-76题2.1.1（4）图(5) 实验测的某有源二端线性网络的开路电压为10V，当外接3Ω的电阻时，其端电压为6V，则该网络的戴维南等效电压的参数为(C)。

(a)U S=6V，R0=3Ω (b)U S=8V，R0=3Ω (c)U S=10V，R0=2Ω(6) 实验测得某有源二端线性网络的开路电压为6V，短路电流为3A。

当外接电阻为4Ω时，流过该电阻的电流I为( A )。

(a)1A (b)2A (c)3A(7) 在图2-77所示电路中，已知U S1=4V，U S2=4V，当U S2单独作用时，电阻R中的电流为1MA，那么当U S1单独作用时，电压U AB是（A）（A）1V （B）3V （C）-3V图2-77题2.1.1（7）图（8）一个具有几个结点，b条支路的电路，其独立的KVL方程为（B）a)（n-1）个 b)（b-n+1）个（9）一个具有几个结点，b条支路的电路，要确定全部支路电流，最少要测量（B）a)（n-1）次 b)（b-n+1）次（10）一个具有n个结点，b条支路的电路，要确定全部支路电压，最少要测量（A）a)（n-1）次 b)（b-n+1）次（11）电阻并联时，电阻值越大的电阻：（A）a)消耗功率越小； b)消耗功率越大。