计量资料的统计推断-t检验
- 格式:ppt
- 大小:1.04 MB
- 文档页数:117




《计量资料的统计推断》的复习思考题1.什么是统计推断?统计推断包括哪两方面内容?2.什么样的分布是t分布?对称分布、正态分布、t分布和标准正态分布有何区别和联系?3.什么是标准误?标准差和标准误有什么区别和联系?4.什么是总体均数的可信区间?某指标的95%正常值范围和95%可信区间有何区别何联系?5.显著性检验的目的意义是什么?基本原理是什么?前提条件有哪些?6.什么情况下可认为具有可比性?举例说明日常生活中常犯的没有可比性时进行比较的错误。
7.显著性检验的一般步骤有哪些?8.显著性检验时,假设有几种?哪几种?如何假设?9.假设检验时,如何选择进行单侧或双侧检验?10.什么是检验水准/显著性水平?一般是多少?如何根据实际情况来确定检验水准?11.假设检验时的“P值”是什么?举例说明。
12.统计学结论和实际意义有何异同?13.什么情况下应该作u/z检验?什么情况下应该作t检验?14.举例说明成组设计和配对设计有何区别。
15.有人说,“只要是比较两个均数,都可以作t检验。
”你认为这种说法对吗?为什么?16.什么是I类错误?什么是II类错误?为什么显著性检验时会犯这两类错误?这两类错误各有什么特点?相互之间有什么关系?17.什么是把握度?科学研究时如何才能使把握度达到一定的水平?18.为什么说统计学结论是概率性的,既不绝对肯定,也不绝对否定?19.随机抽取某品种2月龄苗猪25头,测得其平均体重为20kg,标准差为3kg。
试估计该品种2月龄苗猪的体重。
20.随机测得100听某批某种罐头净重量平均为344.0g,标准差为4.43g。
试估计该批该种罐头的净重量和正常值范围。
21.某鱼场按常规方法所育鲢鱼苗一月龄的平均体长为7.25cm,标准差为1.58cm。
为提高鱼苗质量,现采用一新方法进行育苗,一月龄时随机抽取100尾进行测量,测得其平均体长为7.65cm。
试问新方法能否使一月龄鲢鱼苗体长更长?22.某名优绿茶含水量标准为不超过5.5%。

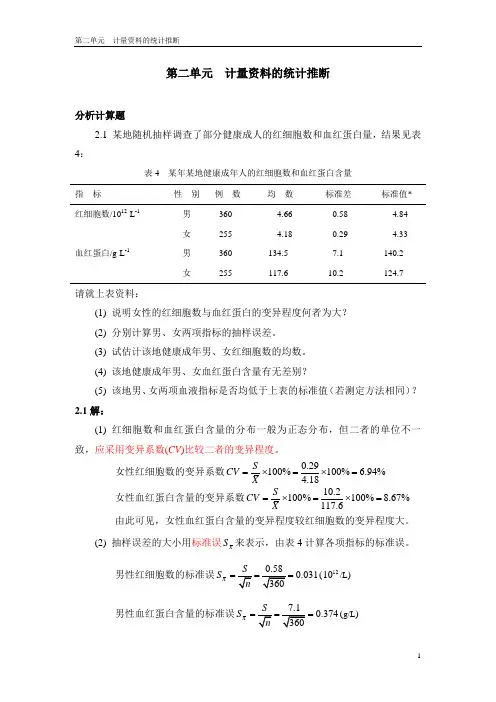
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量,结果见表4:表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数 标准差 标准值* 红细胞数/1012·L -1 男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料:(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大? (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别?(5) 该地男、女两项血液指标是否均低于上表的标准值(若测定方法相同)? 2.1解:(1) 红细胞数和血红蛋白含量的分布一般为正态分布,但二者的单位不一致,应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见,女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示,由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100,可视为大样本。
σ未知,但n 足够大 ,故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。

医学统计学计量资料的统计推断主要内容:标准误t 分布总体均数的估计假设检验均数的 t检验、u 检验、方差分析几个重要概念的回顾:计量资料:总体:样本:统计量:参数:统计推断:参数估计、假设检验第一节均数的抽样误差与总体均数的估计欲了解某地2000年正常成年男性血清总胆固醇的平均水平,随机抽取该地200名正常成年男性作为样本。
由于存在个体差异,抽得的样本均数不太可能恰好等于总体均数。
一、均数的抽样误差与标准误一、均数的抽样误差与标准误抽样误差:由于抽样引起的样本统计量与总体参数之间的差异X数理统计推理和中心极限定理表明:1、从正态总体N(??,??2)中,随机抽取例数为n的样本,样本均数??X 也服从正态分布;即使从偏态总体抽样,当n足够大时??X也近似正态分布。
2、从均数为??,标准差为??的正态或偏态总体中抽取例数为n的样本,样本均数??X的总体均数也为??,标准差为X标准误含义:样本均数的标准差计算:(标准误的估计值)注意: X 、S??X均为样本均数的标准误标准误意义:反映抽样误差的大小。
标准误越小,抽样误差越小,用样本均数估计总体均数的可靠性越大。
标准误用途:衡量抽样误差大小估计总体均数可信区间用于假设检验二 t 分布对正态变量样本均数??X做正态变换(u变换):X 常未知而用S??X估计,则为t变换:二、 t 分布t值的分布即为t分布t 分布的曲线:与??有关t分布与标准正态分布的比较1、二者都是单峰分布,以0为中心左右对称2、t分布的峰部较矮而尾部翘得较高说明远侧的t值个数相对较多即尾部面积(概率P值)较大。
当ν逐渐增大时,t分布逐渐逼近标准正态分布,当ν→??时,t分布完全成为标准正态分布t 界值表(附表9-1 )t??/2,??:表示自由度为??,双侧概率P为??时t的界值t分布曲线下面积的规律:中间95%的t值:- t0.05/2,?? ?? t0.05/2,??中间99%的t值:- t0.01/2,?? ?? t0.01/2,??单尾概率:一侧尾部面积双尾概率:双侧尾部面积(1) 自由度(ν)一定时,p与t成反比;(2) 概率(p)一定时,ν与t成反比;三总体均数的估计统计推断:用样本信息推论总体特征。




t检验的原理方法选择和应用条件一、t检验的原理t检验是一种统计分析方法,用于比较两个样本均值是否存在显著差异。
其原理基于样本数据的均值和标准差,以及样本大小。
通过计算t值,可以判断两个样本之间的差异是否显著。
二、t检验的方法选择根据研究问题和实验设计的不同,可以选择不同的t检验方法。
以下是常见的t检验方法:1.单样本t检验:用于比较一个样本的均值与已知的总体均值之间是否存在显著差异。
适用于总体标准差未知的情况。
2.独立样本t检验:用于比较两个独立样本的均值是否存在显著差异。
适用于两个样本之间相互独立、总体标准差未知的情况。
3.配对样本t检验:用于比较同一组样本在不同条件下的均值是否存在显著差异。
适用于两个样本之间存在相关性、总体标准差未知的情况。
根据研究目的和数据特点,可以选择适合的t检验方法进行分析。
三、t检验的应用条件为了保证t检验结果的准确性和可靠性,在应用t检验时需要满足一定的条件。
以下是t检验的应用条件:1.样本数据近似正态分布:t检验建立在样本数据近似正态分布的基础上,如果样本数据不满足正态分布,可能会导致结果不准确。
2.样本独立性:当进行独立样本t检验时,两个样本应该是互相独立的,即两个样本之间没有相关性。
否则,会导致结果不准确。
3.总体标准差未知:t检验假设总体标准差未知,当已知总体标准差时,可以使用z检验进行分析。
如果以上条件都满足,就可以使用t检验进行统计分析。
四、使用t检验的注意事项在应用t检验时需要注意以下几点:1.样本大小:样本大小直接影响t检验的准确性和可靠性,通常样本大小越大,结果越准确。
2.显著性水平:在进行参数估计时,需要设置显著性水平,常见的显著性水平包括0.05和0.01,选择适合的显著性水平可以得到更可靠的结论。
3.效应大小:在比较两个样本均值时,需要考虑效应大小。
如果效应较小,样本大小可能需要更大才能得到显著的结果。
通过合理选择t检验的方法、满足应用条件,并注意上述注意事项,可以更加准确地进行数据分析和结论推断。
《医学统计学》复习资料广西医科大学流行病与卫生统计学教研室2013.1.52012年留学生总复习练习题Part A理论考试题型一、单选题(每题1.5分,共45分。
请在答题卡上将正确答案对应的字母涂黑二、辨析题(每题3分,共15分。
判断对错,并给出理由)三、简答题(每题5分,共10分)四、分析应用题(共30分+10分)Part B练习题一、单选题(每题1.5分,共45分。
请在答题卡上将正确答案对应的字母涂黑)(一)计量资料统计描述1.卫生统计工作的步骤为________。
A.统计研究调查、搜集资料、整理资料、分析资料B.统计资料收集、整理资料、统计描述、统计推断C.统计研究设计、搜集资料、整理资料、分析资料D.统计研究调查、统计描述、统计推断、统计图表2.某病患者5人的潜伏期(天)分别为6,8,5,10,>13,则平均潜伏期为________。
A.5天B.8天C.6~13天D.11天3.算术均数与中位数相比,。
A.抽样误差更大B.不易受极端值的影响C.更充分利用数据信息D.更适用于分布不明及偏态分布资料值为。
4.标准正态分布中,单侧u0.05A.1.96B.0.05C.1.64D.0.0255.统计分析的主要内容有________。
A.统计描述和统计学检验B.区间估计与假设检验C.统计图表和统计报告D.统计描述和统计推断E.统计描述和统计图表6.统计资料的类型包括________。
A.频数分布资料和等级分类资料B.多项分类资料和二项分类资料C.正态分布资料和频数分布资料D.数值变量资料和等级资料E.数值变量资料和分类变量资料7.抽样误差是指________。
A.不同样本指标之间的差别B.样本指标与总体指标之间由于抽样产生的差别C.样本中每个体之间的差别D.由于抽样产生的观测值之间的差别E.测量误差与过失误差的总称8.统计学中所说的总体是指________。
A.任意想象的研究对象的全体B.根据研究目的确定的研究对象的全体C.根据地区划分的研究对象的全体D.根据时间划分的研究对象的全体E.根据人群划分的研究对象的全体9.描述一组偏态分布资料的变异度,宜用________。