统计数据的描述
- 格式:ppt
- 大小:1.95 MB
- 文档页数:93


统计描述与统计推断统计的主要工作就是对统计数据进行统计描述和统计推断。
统计描述是统计分析的最基本内容,是指应用统计指标、统计表、统计图等方法,对资料的数量特征及其分布规律进行测定和描述;而统计推断是指通过抽样等方式进行样本估计总体特征的过程,包括参数估计和假设检验两项内容。
(一)统计描述1.计量资料的统计描述计量资料的统计描述主要通过编制频数分布表、计算集中趋势指标和离散趁势指标以及统计图表来进行。
(1)集中趋势。
指频数表中频数分布表现为频数向某一位置集中的趋势。
集中趋势的描述指标:1)算术平均数。
直接法:x为观察值,n为个数加权法又称频数表法,适用于频数表资料,当观察例数较多时用。
f为各组段的频数。
2)几何平均数(geometric mean)。
几何平均数用符号G表示。
用于反映一组经对数转换后呈对称分布的变量值在数学上的平均水平。
直接法:加权法又称频数表法,当观察例数n较大时,可先编制频数分布表,用此法算几何平均数:3)百分位数(percentile )与中位数(median )。
百分位数是一种位置坐标,用符号x P 表示常用的百分位数有 2.5P 、5P 、50P 、75P 、95P 、97.5P 等,其中25P 、50P 、75P 又称为四分位数。
百分位数常用于描述一组观察值在某百分位置上的水平,多个百分位结合使用,可更全面地描述资料的分布特征。
中位数是一个特定的百分位数即50P ,用符号M 表示。
把一组观察值按从小到大(或从大到小)的次序排列,位置居于最中央的那个数据就是中位数。
中位数也是反映频数分布集中位置的统计指标,但它只由所处中间位置的部分变量值计算所得,不能反映所有数值的变化,故中位数缺乏敏感性。
中位数理论上可以用于任何分布类型的资料,但实践中常用于偏态分布资料和分布两端无确定值的资料。
其计算方法有直接法和频数表法两种。
直接法:当观察例数n 不大时,此法常用,先将观察值按大小次序排列,选用下列公式求M 。



描述性统计报告范文1. 引言此次统计报告旨在对某公司销售数据进行描述性统计分析,以便更好地了解公司的销售情况并提供决策支持。
本报告将从多个维度对销售数据进行分析,包括销售额、销售数量、产品分类等方面。
2. 数据来源本报告所使用的数据来自某公司近一年的销售记录,包括每个产品的销售额、销售数量以及所属的产品分类。
数据完整、准确,可用于对公司销售情况进行全面分析。
3. 销售金额统计首先,对销售金额进行统计分析。
我们计算了每个产品的销售总额以及销售额的平均值、中位数、最大值和最小值,并绘制了销售金额的直方图和箱线图。
销售总额为X万,平均每个产品的销售额为Y万,中位数为Z万。
从直方图和箱线图可以看出销售金额分布大致呈正态分布,大多数产品的销售额集中在中位数附近,但也存在一些销售额较高的产品。
4. 销售数量统计其次,对销售数量进行统计分析。
我们计算了每个产品的销售总数量以及销售数量的平均值、中位数、最大值和最小值,并绘制了销售数量的直方图和箱线图。
销售总数量为N个,平均每个产品的销售数量为M个,中位数为P个。
从直方图和箱线图可以看出销售数量分布相对均匀,大部分产品的销售数量在中位数附近。
5. 产品分类分析除了对销售金额和销售数量的统计分析外,我们还对产品分类进行了分析。
首先,我们列举了所有产品分类以及每个分类下的产品数量。
然后,我们计算了每个分类的销售总额和销售数量,并绘制了销售金额和销售数量的条形图。
从条形图可以清晰地看出不同分类产品的销售情况。
例如,分类A的销售总额最高,而分类B的销售总额最低。
此外,分类C的销售数量最多,而分类D的销售数量最少。
6. 结论通过对销售数据的描述性统计分析,我们可以得出以下结论:•公司的销售总额为X万,平均每个产品的销售额为Y万。
•销售金额的分布大致呈正态分布,多数产品销售额集中在中位数附近。
•公司的销售总数量为N个,平均每个产品的销售数量为M个。
•销售数量相对均匀分布,大部分产品的销售数量集中在中位数附近。


统计调查数据的收集整理与描述引言统计调查是一种重要的研究方法,通过对数据的收集、整理和描述来揭示问题的本质和规律。
本文将介绍统计调查数据的收集、整理和描述的基本步骤和技巧,帮助读者更好地进行统计调查研究。
数据的收集数据的收集是统计调查的第一步,它决定了后续分析的可靠性和准确性。
数据的收集可以通过多种方式进行,包括问卷调查、实地观察、实验设计等。
问卷调查问卷调查是一种常用的数据收集方法,通过向被调查者发放问卷,收集他们的观点、态度、行为等信息。
在进行问卷调查时,需要注意以下几点:•设计合理的问卷:问卷应该具有良好的结构和逻辑,问题应该清晰明了,避免使用含混或引导性的问题。
•确定合适的样本:样本的选择要具有代表性,能够反映出总体的特征。
可以通过随机抽样或分层抽样等方法来获得样本。
•提高回收率:回收率是衡量问卷调查成功与否的重要指标。
可以通过提供奖励、提高问卷的可读性等方式来提高回收率。
实地观察实地观察是通过直接观察被研究对象的行为和环境来收集数据。
在进行实地观察时,需要注意以下几点:•制定观察方案:明确观察对象、观察的时间和地点,制定观察表格或记录表,确保观察的准确性和全面性。
•实施观察:根据观察方案进行实地观察,记录被观察对象的行为、态度和环境等信息。
•提高观察的客观性:观察者应该尽量客观公正地进行观察,避免主观偏见的干扰。
实验设计实验设计是一种控制变量的方法,通过对实验组和对照组的比较来获取数据。
在进行实验设计时,需要注意以下几点:•确定实验目的:明确实验的目的和研究的问题,根据目的选择适当的实验设计方法。
•设计合理的实验组和对照组:实验组和对照组应该具有相似的特性,只在某一变量上存在差异,以便进行比较。
•控制变量:除了要比较的变量外,其他变量应该尽可能保持一致,避免对实验结果的干扰。
数据的整理数据的整理是对收集到的原始数据进行加工和整理,使其更加便于分析和描述。
数据的整理包括数据清洗、数据编码和数据归纳等步骤。
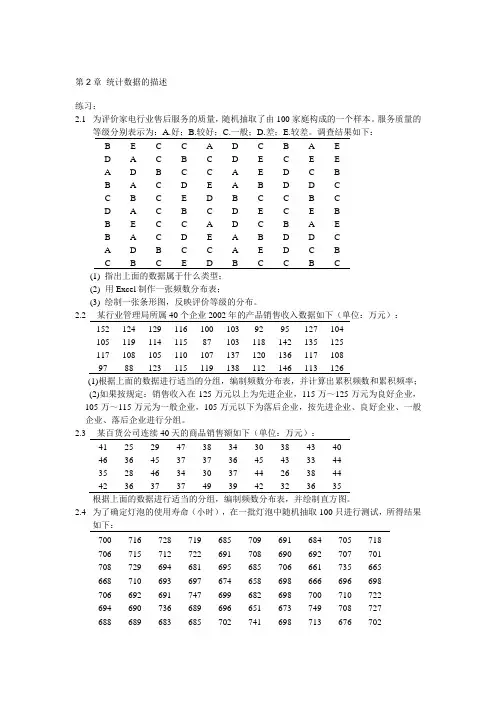
第2章统计数据的描述练习:2.1为评价家电行业售后服务的质量,随机抽取了由100家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C.一般;D.差;E.较差。
调查结果如下:B EC C AD C B A ED A C B C DE C E EA DBC C A ED C BB ACDE A B D D CC B C ED B C C B CD A C B C DE C E BB EC C AD C B A EB ACDE A B D D CA DBC C A ED C BC B C ED B C C B C(1) 指出上面的数据属于什么类型;(2)用Excel制作一张频数分布表;(3) 绘制一张条形图,反映评价等级的分布。
2.2某行业管理局所属40个企业2002年的产品销售收入数据如下(单位:万元):152 124 129 116 100 103 92 95 127 104105 119 114 115 87 103 118 142 135 125117 108 105 110 107 137 120 136 117 10897 88 123 115 119 138 112 146 113 126(1)根据上面的数据进行适当的分组,编制频数分布表,并计算出累积频数和累积频率;(2)如果按规定:销售收入在125万元以上为先进企业,115万~125万元为良好企业,105万~115万元为一般企业,105万元以下为落后企业,按先进企业、良好企业、一般企业、落后企业进行分组。
2.3某百货公司连续40天的商品销售额如下(单位:万元):41 25 29 47 38 34 30 38 43 4046 36 45 37 37 36 45 43 33 4435 28 46 34 30 37 44 26 38 4442 36 37 37 49 39 42 32 36 35根据上面的数据进行适当的分组,编制频数分布表,并绘制直方图。


数据描述性统计分析数据是当今社会中不可或缺的重要资源,通过对数据进行描述性统计分析,可以帮助我们更好地理解数据的特征和规律,为决策提供有力支持。
本文将从数据描述性统计分析的概念、方法和应用等方面进行探讨。
一、概念数据描述性统计分析是指通过对数据的整理、总结、分析和展示,揭示数据的分布规律、集中趋势、离散程度等特征。
在数据分析领域中,描述性统计分析是最基础、最核心的环节,能够直观地帮助我们了解数据的基本情况,为后续的推断性统计分析提供依据。
二、方法1. 数据整理:首先需要对所收集的数据进行整理,包括数据的输入、分类、编码等操作,确保数据的准确性和完整性。
2. 数据总结:接着可以对数据进行总结,包括计算数据的频数、频率、均值、中位数、众数、标准差、方差等统计量,从而揭示数据的集中趋势和离散程度。
3. 数据展示:最后,可以通过图表等形式将数据进行展示,如直方图、饼图、折线图等,直观地展现数据的分布情况,有助于我们更好地理解数据。
三、应用数据描述性统计分析在各个领域都有着广泛的应用,下面以几个典型领域为例进行介绍:1. 商业领域:在市场调研、销售预测等方面,可以通过对数据的描述性统计分析,快速获取市场需求、产品销售情况等信息,为企业决策提供支持。
2. 医疗领域:在医学研究、疾病预防等方面,可以通过对患者的病例数据进行描述性统计分析,揭示疾病的发病率、治疗效果等信息,为医疗保健提供参考。
3. 教育领域:在学生考试成绩、学科发展等方面,可以通过对学生成绩数据进行描述性统计分析,了解学生学习情况、课程难易度等信息,为教学改进提供依据。
综上所述,数据描述性统计分析作为一种重要的数据分析手段,在各个领域都有着广泛的应用,能够帮助我们更好地理解数据、发现问题、做出决策,对推动社会发展和进步具有重要意义。
希望本文对读者有所启发,促进更多人深入了解和应用数据描述性统计分析。

统计描述的基本概念统计描述的基本概念统计描述是指对数据进行总结、分析和解释的过程,它是统计学中最基本的内容之一。
在实际应用中,统计描述可以帮助我们更好地理解数据,并从中发现规律和趋势,为决策提供支持。
本文将从以下几个方面对统计描述的基本概念进行详细介绍。
一、数据类型在进行统计描述之前,我们需要了解数据类型。
常见的数据类型包括:1. 数值型:数值型数据是指可以用数字表示的数据,如身高、体重、年龄等。
2. 分类型:分类型数据是指不能用数字表示的数据,如性别、颜色、职业等。
3. 顺序型:顺序型数据是指具有一定顺序关系但没有固定数值间隔的数据,如学历、评分等。
4. 时间型:时间型数据是指具有时间属性的数据,如出生日期、交易时间等。
二、中心趋势度量中心趋势度量是指反映一组数据集中位置的度量。
常见的中心趋势度量包括:1. 平均数:平均数是所有数值之和除以样本数量得到的结果。
它可以反映样本整体水平。
2. 中位数:中位数是将一组数据按大小排列后,位于中间位置的数值。
它可以反映样本的中心位置。
3. 众数:众数是一组数据中出现次数最多的数值。
它可以反映样本的典型值。
三、离散程度度量离散程度度量是指反映一组数据分散程度的度量。
常见的离散程度度量包括:1. 方差:方差是各个数据与平均数之差平方和除以样本数量得到的结果。
它可以反映数据分布的离散程度。
2. 标准差:标准差是方差的算术平方根,它与方差具有相同的单位。
它可以反映数据分布的离散程度。
3. 极差:极差是一组数据中最大值与最小值之间的差值。
它可以反映数据分布范围大小。
四、偏态与峰态偏态与峰态是描述数据分布形态特征的指标。
1. 偏态:偏态是指一组数据分布相对于平均数不对称的程度。
如果偏态系数大于0,则表示右偏;如果偏态系数小于0,则表示左偏;如果偏态系数等于0,则表示对称。
2. 峰态:峰态是指一组数据分布的峰度特征。
如果峰态系数大于0,则表示尖峭;如果峰态系数小于0,则表示平坦;如果峰态系数等于0,则表示正常。
print("d列的累加和结果为e列:\n",data[['d','e']])输出结果如图4-*所示。
图4-* 统计指标计算示例结果2.利用describe函数进行计算pandas提供了describe函数用来一次性计算数值型字段的八个统计指标,如表3-*所示。
表4-* 数值型字段的describe函数统计结果方法名称说明count 非空个数mean 均值std 标准差min 最小值25% 25%分位数50% 50%分位数,即中位数75% 75%分位数max 最大值在调用describe函数计算统计指标时,还可以采用describe()[i](i=0,1,2,…)的方法调用某个统计指标,如用describe()[0]调用第1个统计指标count,describe()[1]调用第2个统计指标mean。
同时,还可以利用指标名称来调用指标,如describe()['25%']表示调用25%分位数,即调用下四分位数。
示例代码如下:des = data['a'].describe()print("a列的describe函数计算结果:\n",round(des,2)) #利用round函数保留所有2位小数print("a列的平均值= ",des[1])print("a列的25%分位数= ",des['25%'])输出结果如图4-*所示。
图4-* 统计指标计算示例结果二、分类型字段的统计与描述分类型字段是指该字段的具有分类作用,如省份名、城市名、商品类别等,分类型字段统计与描述主要是频数统计。
1.利用value_counts函数进行统计分析pandas提供了value_counts函数用来统计分类型字段的频数,value_counts函数的一般用法为:value_counts(normalize,ascending)其中,normalize表示是否按频率显示,True表示按频率显示,False表示按频数显示,默认为False,即默认按按频数显示。
描述统计的方法一、统计表和绘图的区别。
有时候我们想从一个数字中看出它所代表的含义,怎么办呢?这就需要用到描述统计了。
下面我将给大家介绍两种表示统计的方法:让我们先来认识一下描述统计的方法。
描述统计又称参数估计,是根据样本的观测值,对总体的未知参数做出概率估计的过程。
通常的方法有两种:一种是点估计法,另一种是区间估计法。
点估计法:对所要研究的问题用样本观察值,对总体参数进行估计;或者假定总体的某些未知参数为已知,从而来确定待估计参数。
这种估计法比较简单,也比较直观,但其精度不高,适合于解决少量的总体参数估计问题。
点估计法包括一阶点估计和二阶点估计。
二阶估计在概率论中被称为点估计的有效估计,它的精度最高。
但由于一阶估计有限,所以在实际应用中,只用一阶估计。
现在,我们再来谈谈绘图的方法。
绘图的方法包括单纯形法、几何作图法等。
单纯形法是由格点法演变而来的。
单纯形法绘图的步骤是:选择一组观测数据,在坐标纸上绘制相关点;找出这组数据的单纯形曲线;检查每条单纯形曲线的极差是否符合要求。
这种方法简单易行,它能表示出数据的离散情况,是最基本的统计图形。
它可以表示出许多类型的数据,如点数、百分数、平均数、差数、标准差、极差等。
描述统计不仅可以用于自然科学,还可以用于社会科学。
一般地说,在自然科学里描述统计更多的应用于随机现象的统计规律性研究。
如果把随机现象视为许多元素之间的函数关系,那么研究随机现象发生的规律,也就是描述各个元素之间的函数关系。
在社会科学中,描述统计主要应用于社会调查、人口统计、经济预测、财政金融、保险管理等。
二、描述统计与假设检验。
统计推断的第一步是提出统计假设。
这是统计推断的关键。
如果没有提出正确的统计假设,就不能进行统计推断。
因此,提出好的统计假设是非常重要的。
在描述统计中,要对总体数据进行某种推断,必须提出一个假设,这就叫做统计假设。
如要探讨总体数据与哪些因素之间存在着某种关系,则要提出该关系的一种可能性,即做出假设H: P=f( x)。
第二章统计数据的描述【说明】(一)统计数据的分类、表达形式1.按数据的计量尺度不同划分•分类数据---列名尺度、定类尺度、名义尺度的计量结果对事物进行分类的结果,数据表现为类别,用文字来表述⏹表现为类别,用文字来表述⏹•顺序数据----定序尺度的计量结果对事物类别顺序的测度⏹数值型数据----定距尺度、定比尺度的计量结果⏹对事物的精确测度⏹结果表现为具体的数值⏹2.按采集方法划分1、观测数据(observational data)2、试验数据(experimental data)3.按时间状况划分•截面数据(cross-sectional data)在相同或者近似相同的时间点上采集的数据⏹描述现象在某一时刻的变化情况⏹•时间序列数据(time series data)在不同时间上采集到的数据⏹描述现象随时间变化的情况⏹(二)数据的表现形式绝对数按其所反映的时间状况不同,划分为:时期数、时点数⏹(计量单位有实物单位、价值单位、复合单位)相对数包括:比例(Proportion)、比率(Ratio)⏹(计量单位有百分比、千分比)统计数据的描述过程一、第一个环节——统计数据的搜集(一)统计数据的来源(渠道)(二)统计数据的搜集方式、方法(三)统计数据的质量要求(评价标准)1. 精度:最低的抽样误差或者随机误差2. 准确性:最小的非抽样误差或者偏差3. 关联性:满足用户决策、管理和研究的需要4. 及时性:在最短的时间里取得并发布数据5. 一致性:保持时间序列的可比性6. 最低成本:以最经济的方式取得数据二、第二个环节——统计数据的整理【重点】数据的整理与显示的基本原则:要弄清所面对的数据类型,因为不同类型的数据,所采取的处理方式和方法是不同的;•对分类数据和顺序数据主要是进行分类整理;•对数值型数据则主要是进行分组整理;•适合于低层次数据的整理和显示方法也适合于高层次的数据;但适合于高层次数据的整理和显示方法并不适合于低层次的数据。