下载文档原格式
微观经济学考研复习考点之生产函数凯程晶晶老师整理了微观经济学考研的基础考点之一生产函数，分享给考研有需要的同学们。
生产要素：从事生产所必须投入的各种人力、物力、财力，都叫生产要素。
包括自然资源、资本投资、劳动技术、企业才能。
生产函数：描述在一定时期内，在一定技术条件下，生产中所使用的各种生产要素的数量与所能生产的最大产量之间关系的函数。
投入分为固定投入和变动投入。
固定投入指当市场条件变化要求产出变化时，其投入不能立即随之变化的投入。
变动投入是指当市场条件变化要求产出变化时，其投入量能够立即随之变化的投入。
在经济学中通常假定生产中只使用劳动和资本这两种生产要素，L表示劳动投入数量，K表示资本投入数量，Q=f(L,K)短期指生产者来不及调整全部生产要素的数量，至少有一种生产要素的数量是固定不变的时间周期。
长期指生产者可以调整全部生产要素的数量的时间周期。
短期和长期的划分是以生产者能否变动全部要素投入的数量作为标准的。
劳动的总产量指与一定的可变要素劳动的投入量相对应的最大产量。
劳动的平均产量指平均每一单位可变要素劳动的投入量所生产的产量。
劳动的边际产量指增加一单位可变要素劳动的投入量所增加的产量。
边际产量是指增加一单位可变要素投入量所增加的产量。
边际产量的公式定义为：MP=△TP/△x。
厂商经营的最好时期是边际产量递增阶段。
这一时期平均产量和总产量也是随着递增的。
边际产量达到最大值后开始不断递减，影响平均产量和总产量等产量曲线：描述在技术水平不变的情况下，生产同一产量的两种生产要素投入量的所有不同组合的曲线。
其斜率等于边际技术替代率。
边际替代率：表示在产量不变的情况下，每增加一单位的某种生产要素投入时，所需减少的另一种要素投入量。
在维持产量不变的前提下，当一种生产要素投入量增加时，每一单位的这种生产要素的替代生产要素投入量是递减的，这就是边际生产要素递减规律。
固定替代比例的生产函数：在每一产量水平上任何两种生产要素间替代比例是固定的，函数表示为Q=aL+bK。
答：规模报酬的递增、不变和递减这三种情况与可变化比例生产函数的报酬递增、不变和递减的区别如下：规模报酬问题论及的是，一厂商的规模本身发生变化（这假定为该厂的厂房、设备等固定要素和劳动、原材料等可变要素发生了同比例变化）相应的产量是不变、递增还是递减，或者说是厂商根据他的经营规模大小（产销量大小）设计不同的工厂规模；而可变比例生产函数所讨论的则是在该厂的规模已经固定下来，即厂房、设备等固定要素既定不变，可变要素的变化引起的产量（报酬）递增、递减及不变等三种情况。
“规模报酬递增的厂商不可能也会面临要素报酬递减的现象”。
这个命题是错误的。
规模报酬和可变要素报酬是两个不同的概念。
规模报酬问题讨论的是一座工厂本身规模发生变化时产量的变化，而可变要素报酬问题论及的则是厂房规模已经固定下来，增加可变要素时相应的产量变化。
事实上，当厂商经营规模较大，在给定技术状况下投入要素的效率提高，即规模报酬递增的同时，随着可变要素投入增加到足以使固定要素得到最有效的利用后，继续增加可变要素，总产量的增加同样将会出现递减现象。
所以规模报酬递增的厂商可能也会同时面临报酬递减现象。
张元鹏《微观经济学》（中级教程）第五章 生产者行为理论（Ⅰ）复习笔记跨考网独家整理最全经济学考研真题，经济学考研课后习题解析资料库，您可以在这里查阅历年经济学考研真题，经济学考研课后习题，经济学考研参考书等内容，更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验，从前辈中获得的经验对初学者来说是宝贵的财富，这或许能帮你少走弯路，躲开一些陷阱。
以下内容为跨考网独家整理，如您还需更多考研资料，可选择经济学一对一在线咨询进行咨询。
一、生产技术与生产函数 1．企业及其生产技术生产活动的主体是企业，也称厂商，是指可以对生产和销售做出统一决策，且努力将若干种投入转化为产出的经济单位。
投入与产出间的数量关系反映了企业在一定时期内的技术关系或状况。
技术不是指企业生产过程中的技术细节，而是指企业将投入转化为产出的能力。
2．生产集在完全竞争的假定下，企业产出的多少归根到底取决于企业的技术能力，即将投入品转化为产出品的能力，这种能力可以用生产集来描述。
生产集是指一定技术条件下企业的投入与产出之间的各种组合的集合。
如图5-1阴影部分所示。
图5-1 生产集3．生产函数生产函数的一般可表述为：()12,,,n Q f x x x =⋯⋯。
该生产函数说明：（1）对于任一给定的生产要素投入量，现有的生产技术给出了一个最大的产出量； （2）对于任一给定的产出量Q ，每一投入组合的使用量为最小。
为简化分析，对于投入一般只考虑劳动（L ）和资本（K ）两个要素，因此，简化后的生产函数可表示为：(),Q f L K =4．常见的生产函数的形式 （1）线性生产函数线性生产函数或称完全替代技术的生产函数，其表达式为：(),Q f L K aL bK ==+其中，a 和b 均为大于零的常数。
该生产函数的经济含义是，按这种生产函数安排生产时，企业只会使用两种要素中较便宜的一种，而不会同时使用两种投入要素，即两种要素之间可以完全替代。
（2）固定投入比例生产函数固定投入比例生产函数，或者称为完全互补技术的生产函数，其表达式为：(),min L K Q f L K a b ⎧⎫==+⎨⎬⎩⎭其中，a 和b 分别为大于零的常数，它们常被看做劳动和资本的技术系数，分别表示了生产一单位产量所需要的固定的劳动投入量和资本投入量。
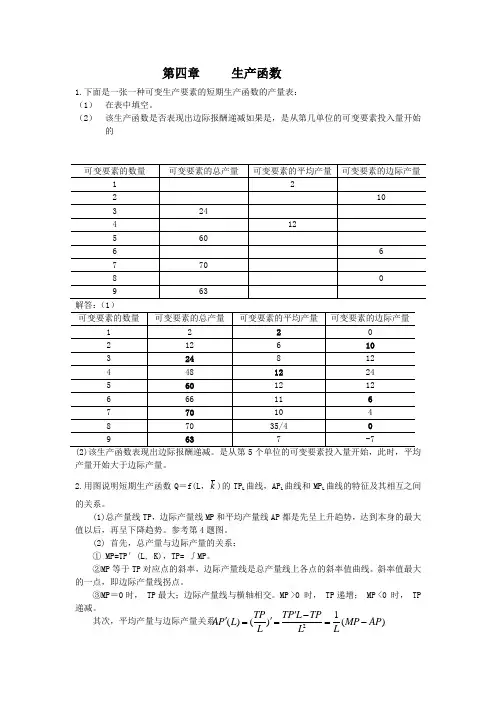
第四章 生产函数1.下面是一张一种可变生产要素的短期生产函数的产量表： （1） 在表中填空。
（2） 该生产函数是否表现出边际报酬递减如果是，是从第几单位的可变要素投入量开始的(2)该生产函数表现出边际报酬递减。
是从第5个单位的可变要素投入量开始，此时，平均产量开始大于边际产量。
2.用图说明短期生产函数Q ＝f(L ，k )的TP L 曲线，AP L 曲线和MP L 曲线的特征及其相互之间的关系。
(1)总产量线TP ，边际产量线MP 和平均产量线AP 都是先呈上升趋势，达到本身的最大值以后，再呈下降趋势。
参考第4题图。
(2) 首先，总产量与边际产量的关系： ① MP=TP ′(L, K)，TP= ∫MP 。
②MP 等于TP 对应点的斜率，边际产量线是总产量线上各点的斜率值曲线。
斜率值最大的一点，即边际产量线拐点。
③MP ＝0时， TP 最大；边际产量线与横轴相交。
MP >0 时， TP 递增； MP <0 时， TP 递减。
其次，平均产量与边际产量关系。
21()()()TP TP L TP AP L MP AP L L L '-''===-①若MP ＞AP ，则AP 递增；平均产量上升的部分，边际产量一定高于平均产量；②若MP ＜AP ，则AP 递减；平均产量线下降的部分，边际产量线一定低于平均产量线。
③若MP ＝AP ，则AP 最大。
MP 交AP 的最高点。
最后，总产量与平均产量的关系。
①AP=TP/L②原点与TP 上一点的连线的斜率值等于该点的AP 。
③从原点出发与TP 相切的射线，切点对应AP 最大。
3.已知生产函数Q ＝f(L ，K)=2KL- ，假定厂商目前处于短期生产，且K ＝10，求：(1)写出在短期生产中该厂商关于劳动的总产量TP L 函数、劳动的平均产量AP L 函数和劳动的边际产量MP L 函数。
(2)分别计算当总产量TP L 、劳动平均产量AP L 和劳动边际产量MP L 各自达到极大值时的厂商劳动的投入量。
