第六讲生产函数与规模报酬

(1)不是齐次函数。

因为f tx,ty =t 3x 3 -t 2xy ，t 3y 3 =tf x, y 。

平新乔《微观经济学十八讲》第 6讲 生产函数与规模报酬1 •生产函数为 Q - _KL2 ・16L _18，工人工资为 w =8，产品价格为p =1。

计算：(1)短期内K =2，最优劳动投入是多少？(2) 最大平均产量的劳动投入为多少？此时的最大平均产量是多少？解: (1 )在短期内K =2，则厂商的生产函数为 Q- -2 L 2・16L —18，则可得厂商的利润 函数为：2二 L = pQ L -wL - -2L 8L -18利润最大化的一阶条件为：d4L 8=0 dL解得L =2，此即为短期内的最优劳动投入量。

(2) 由生产函数 ^_2L 2 16L -18，可得平均产量函数为:AP L =Q=-21_北6L平均产量最大化的一阶条件为:L =3 (负值舍去)。

故最大平均产量的劳动投入为 此时的最大平均产量为 AR =Q =-2L +16—些=4。

L L2 •确定下列函数是不是齐次函数，如果是，规模报酬情况如何？ (1) f x,y =x3 _xy y 3 (2) f x,y =2x y 3 xy 1/2■ 43 1/6(3) f x,y,w = x -5yw答：若函数f x,y 满足f tx,ty 二t k f x,y ，则称函数f x,y 为k 次齐次函数。

同时由 规模报酬的定义可知， 若f tx,ty j=tf x,y ,则为规模报酬不变； 若f tx,ty tf x,y ,贝U 为规模报酬递增；若f tx,ty ::: tf x,y ,则为规模报酬递减。

dtQ-18 L 2解得:(2) 是齐次函数，且规模报酬不变，因为 f tx,ty=2tx ty 3t xy三二tf x, y 。

(3) 是齐次函数，且规模报酬递减，因为：1 2 1 24 4 4 3 c ? 4 3 c艾f tx,ty,tw = t x - 5t yw =t x - 5yw =t f x,y,w ; tf x, y, w3 •设某省有一个村庄，该村既生产粮食又会织布。

第六讲 生产函数与规模报酬现转向经济中的供给方，研究人们消费的商品和劳务的生产过程。

供给方是由一系列被称为企业的生产单位组成。

企业可以是公司，也可以是其它合法的组织。

§1 基本概念一、生产要素：L （labor ），K （capital ），L d （land ）生产是将投入转化为产出的过程。

生产的投入叫生产要素。

生产要素包括：土地、劳动和资本。

生产技术指生产的投入要素与产出量之间的关系，通常表现为一种可行的生产计划表。

只有某些投入组合才有可能生产即定的产出量。

二、企业面临的约束企业的产生？谁拥有它？谁来管理它？它是怎样运作的？它是怎样组织的？它能做些什么？关于企业有一系列的问题，我们将集中讨论最后一个，即生产多少。

于是我们假定企业是一个能够将投入转化为产出的“黑匣子”。

而且，企业在做决策时都以利润最大化作为目标。

原因在于：一些行为符合利润最大化目标。

以利润最大化所得理论得到了实际支持；其替代性的目标，如市场份额最大化，可被视为企业的长期利润最大化战略中的短期策略，而不是企业的终极目标；市场力量强制厂商走向利润最大化。

如果未做到利润最大化，是由于经理造成的，则所有者会更换经理；若是由于所有者造成的，其他企业会购并该企业。

企业在决策时，也面临许多约束条件。

包括客户、竞争对手、自然条件等，归纳起来有：（1）资金约束（预算约束）：0d C w L r K q L ≤⋅+⋅+⋅（在我国，软约束）：你有多少资金可用于生产和投资？（2）市场需求约束：市场对你的产品究竟需要多少？（3）生产技术约束：即使你有了钱，买了设备、原材料，请了工人，也有市场需求，但你能生产多少？ 三、生产集生产集是技术上可行的所有投入与产出组合的集合。

技术表明的单一组合可以用不同的方法加以利用，从而产生许多不同的产出水平。

生产函数与技术不同。

生产集为凸集，即：()00,x y x ∈，()11,x y x ∈则()011x x x λλ+-∈。

平新乔《微观经济学十八讲》第6讲 生产函数与规模报酬1．生产函数为21618Q KL L =-+-，工人工资为8w =，产品价格为1p =。

计算：（1）短期内2K =，最优劳动投入是多少？（2）最大平均产量的劳动投入为多少？此时的最大平均产量是多少？解：（1）在短期内2K =，则厂商的生产函数为221618Q L L =-+-，则可得厂商的利润函数为：()()22818L pQ L wL L L π=-=-+-利润最大化的一阶条件为：d 480d L Lπ=-+= 解得2L =，此即为短期内的最优劳动投入量。

（2）由生产函数221618Q L L =-+-，可得平均产量函数为：18216L Q AP L L L==-+-平均产量最大化的一阶条件为：2d 1820d Q L L L⎛⎫=-+= ⎪⎝⎭ 解得：3L =（负值舍去）。

故最大平均产量的劳动投入为3。

此时的最大平均产量为182164L Q AP L L L==-+-=。

2．确定下列函数是不是齐次函数，如果是，规模报酬情况如何？ （1）()33,f x y x xy y =-+ （2）()()1/2,23f x y x y xy =++ （3）()()1/643,,5f x y w x yw =-答：若函数(),f x y 满足()(),,k f tx ty t f x y =，则称函数(),f x y 为k 次齐次函数。

同时由规模报酬的定义可知，若()(),,f tx ty tf x y =，则为规模报酬不变；若()(),,f tx ty tf x y >，则为规模报酬递增；若()(),,f tx ty tf x y <，则为规模报酬递减。

（1）不是齐次函数。

因为()()33233,,f tx ty t x t xy t y tf x y =-+≠。

（2）是齐次函数，且规模报酬不变，因为()()()12,23,f tx ty tx ty t xy tf x y =++=。

生产函数q=f的规模报酬变化趋势生产函数是用来描述输入要素（如劳动力和资本）与产出（如商品或服务）之间的关系的函数。

规模报酬变化趋势是指在输入要素的规模扩大或缩小时，产出相应地如何变化的趋势。

规模报酬变化可以分为三种情况：递增报酬、递减报酬和常量报酬。

递增报酬递增报酬是指当输入要素的规模扩大时，产出的增长速度大于输入要素的增长速度。

在这种情况下，生产函数呈现出递增的规模报酬，即边际产出递增。

递增报酬通常发生在投入要素的有效利用程度不够高时。

例如，在劳动密集型行业中，当雇佣更多的劳动力时，生产效率提高，从而导致产出的增长速度超过劳动力的增长速度。

此外，还可能有技术进步、专业化和分工的提高等因素影响了递增报酬的发生。

递减报酬递减报酬是指当输入要素的规模扩大时，产出的增长速度小于输入要素的增长速度。

在这种情况下，生产函数呈现出递减的规模报酬，即边际产出递减。

递减报酬通常发生在投入要素的限制条件下，增加输入要素并不能完全被有效利用。

例如，在资本密集型行业中，当增加了太多的资本，劳动力的利用程度将下降，从而导致产出的增长速度小于资本的增长速度。

递减报酬可能还受到生产函数的特性以及市场条件的影响。

例如，技术效率的下降以及市场需求的变化都可能导致递减报酬的发生。

常量报酬常量报酬是指当输入要素的规模扩大时，产出的增长速度等于输入要素的增长速度。

在这种情况下，生产函数呈现出常量的规模报酬，即边际产出恒定。

常量报酬通常发生在输入要素的利用程度已经达到最大，随着输入要素的增加，产出的增长速度趋于平稳。

例如，在车间生产线上，增加更多的劳动力和资本并不能显著提高产能，因为生产线的运作已经达到了最大化。

总结而言，生产函数的规模报酬变化趋势取决于输入要素的增长速度以及其利用程度。

递增报酬发生在输入要素利用程度不够高的情况下，递减报酬发生在输入要素受限制的情况下，而常量报酬则发生在输入要素达到最大利用程度的情况下。

理解规模报酬变化趋势对于企业决策和经济增长的分析非常重要。

生产函数与规模报酬1. 引言生产函数和规模报酬是经济学中重要的概念，用于研究企业的生产能力和生产效率。

通过研究生产函数和规模报酬，可以帮助企业提高生产效率，提高产品质量，并提供决策依据。

2. 生产函数生产函数是描述输入和产出之间关系的函数。

它显示了生产过程中各种输入要素与产出之间的关系。

生产函数通常用数学模型表示，常见的模型包括线性模型、二次模型、指数模型等。

生产函数的一般形式可以表示为：Y = f(X1, X2, ..., Xn)其中，Y表示产出，Xi表示各种输入要素，f表示生产函数。

生产函数可以是多元函数，也可以是单元函数。

生产函数的具体形式取决于具体的生产过程和生产要素。

生产函数有几个重要的特性： - 递增边际产出：生产函数通常表现为递增边际产出，即每增加一个输入要素，会带来更多的产出增加。

- 递减边际产出：当输入要素持续增加时，生产函数的边际产出逐渐递减，即每增加一个额外的输入要素，产出的增加效果变小。

- 规模不变报酬：当输入要素按比例增加时，生产函数的产出也按相同比例增加，称为规模不变报酬。

- 递增规模报酬：当输入要素按比例增加时，产出增加的比例超过输入要素增加的比例，称为递增规模报酬。

- 递减规模报酬：当输入要素按比例增加时，产出增加的比例低于输入要素增加的比例，称为递减规模报酬。

3. 规模报酬规模报酬是指在一定时期内，企业通过增加所有输入要素的数量，达到增加产出数量的效果。

规模报酬可分为三种类型：递增规模报酬、递减规模报酬和规模不变报酬。

3.1 递增规模报酬递增规模报酬是指在保持输入要素的比例不变的情况下，增加所有输入要素的数量，从而使得产出数量增加的情况。

递增规模报酬表示企业规模的扩大对产出的影响是正向的，即规模越大，产出越多。

递增规模报酬通常出现在企业初期，当企业的规模较小时，通过增加投入资源，可以更充分地利用经济规模优势，提高产出。

递增规模报酬有助于企业降低单位成本，提高经济效益。

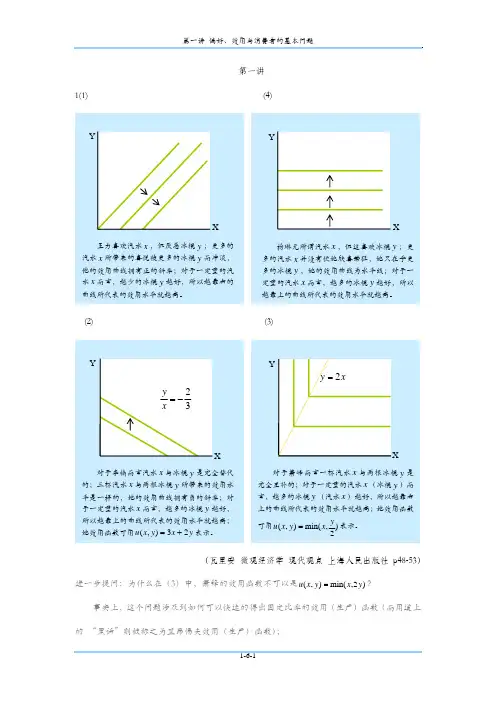
第六讲生产函数与规模报酬第六讲3为了分析更为直观，我们先看第二段，从中可画出其生产转换曲线。

粮食38 设这个村庄只有一块地，可30 种植粮食和棉花，而在市场的最终产品为一定担数的粮食和24 坯布，村庄的目的是实现其产品的市场价值最大化。

坯布323850 （1）市场上的每米坯布的价格为1元不变；当每担粮食低于0.5元时，这块地全用来种价格植棉花，生产出50米的坯布，这时，村庄4 实现了最大化的市场价值50元；当每担粮食的价格为0.5元时，无论这块地全种植棉花，还是其中一部分种植粮食、一部分种植棉花而得出的24担粮食和38米坯布，其市场价值均为50元；同理，当每担粮食为1元时，则生产30担粮食和32米坯布或是24担粮食和38米坯布，其市场价值1 均为62元，；而当每担粮食为4元时，则0.5 倾其全部的土地来种植粮食或是30担粮食243038和32米坯布，其最终市场价值均为152元。

粮食（2）同上的分析，市场的每担粮食的价价格格为1元不变；当每米坯布的价格低于0.25元时，全部产粮食；等于0.25元时，0米坯布，38担粮食或是32米坯布和302 担粮食；等于1元时32米坯布和30担粮食或是38米坯布和24担粮食；等于2元时，38米坯布和24担粮食或全用来种1 植棉花都将产生100元的价值；大于2元时，全部种植棉花来生产坯布。

0. 25 因为根据题设条件，我们只能得出5032 38“离散”型的供给曲线。

坯布6-8-1 2005-12-13 18:29:04 第六讲生产函数与规模报酬1 （1）设资本投入的价格为v，则：2π=pQ??wL??vK=(??2L+16L??18)??8L??2v2dπdπ=??4L+16??8=0；=??4&lt;0 2dLdLL=2 Q18（2）AL==??2L+16?? LL2dAL18dAL18=??2+=0；=??2&lt;0 223dLLdLLL=32Q??2×3+16×3??18AQ ===4L333233k2 （1）f(tx.ty)=tx??txy+ty≠tf(x,y)k为常数112（2）2f(tx.ty)=2tx??ty+3t(xy)=t2x+y+3(xy)=tf(x,y) 规模报酬不变21243363（3）f(tx,ty,tw)=t(x??5yw)=tf(x,y) 规模报酬递减5（1）??边际产出大于零时，总产量将随着投入的增加而上升，这是因为边际产出实为总产量的斜率；当边际产出大于平均产出??时，平均产出上升，当边际产出小于平均产出时，平均产出下降。