ARMA模型介绍

ARMA相关模型及其应用一、本文概述随着科技的快速发展和数据分析技术的不断进步，时间序列分析在金融、经济、工程等领域的应用日益广泛。

其中，自回归移动平均模型（ARMA模型）作为一种重要的时间序列分析工具，其理论和实践价值备受关注。

本文旨在深入探讨ARMA模型的基本理论、性质及其在实际问题中的应用，旨在为读者提供一个全面而深入的理解和应用ARMA模型的参考。

本文将简要介绍ARMA模型的基本概念、发展历程及其在时间序列分析中的地位。

随后，重点阐述ARMA模型的数学原理、参数估计方法以及模型的检验与优化。

在此基础上，本文将通过具体案例，展示ARMA模型在金融市场分析、经济预测、工程信号处理等领域的实际应用，并探讨其在实际应用中的优势与局限性。

本文旨在为研究者、学者和实践者提供一个关于ARMA模型及其应用的全面指南，帮助他们更好地理解和应用这一重要的时间序列分析工具。

通过案例分析，本文旨在为相关领域的学者和实践者提供新的思路和方法，推动ARMA模型在实际问题中的更广泛应用。

二、ARMA模型基础ARMA模型，全称为自回归移动平均模型（AutoRegressive Moving Average Model），是时间序列分析中的一种重要模型。

它结合了自回归模型（AR，AutoRegressive）和移动平均模型（MA，Moving Average）的特点，能够更全面地描述时间序列数据的动态变化特性。

ARMA模型的基本形式为ARMA(p, q)，其中p是自回归项的阶数，q是移动平均项的阶数。

模型的一般表达式为：_t = \varphi_1 _{t-1} + \varphi_2 _{t-2} + \cdots +\varphi_p _{t-p} + \epsilon_t + \theta_1 \epsilon_{t-1} +\theta_2 \epsilon_{t-2} + \cdots + \theta_q \epsilon_{t-q}) 其中，(_t)是时刻t的观察值，(\varphi_i)是自回归系数，(\epsilon_t)是时刻t的白噪声项，(\theta_i)是移动平均系数。

arma模型原理
ARMA模型（AutoRegressive Moving Average Model）是一种时间序列分析模型，它结合了自回归模型（AR）和移动平均模型（MA）。

ARMA 模型的原理是，对于一个时间序列，在保持平稳性的前提下，通过自回归和移动平均两个方面来描述序列的特征。

具体来说，AR表示当前时间点的值与前面若干个时间点的值有关，而MA表示当前时间点的值与前面若干个时间点的噪声有关。

因此，ARMA模型可以很好地捕捉时间序列数据的趋势和周期性。

在实际应用中，ARMA模型通常用于预测未来的时间序列值和分析时间序列的特征。

在ARMA模型中，参数估计和模型检验是重要的步骤，需要一定的统计学知识和技能。

常用的估计方法包括最大似然估计和贝叶斯估计，而模型检验可以通过残差分析和模型诊断来进行。

总之，ARMA模型是一种经典的时间序列模型，它结合了自回归模型和移动平均模型，可以用于预测未来的时间序列值和分析时间序列的特征。

在实际应用中需要谨慎使用，需要考虑时间序列数据的特征和背景知识，以及参数估计和模型检验的可靠性。

arma模型的数学表达式摘要：1.ARMA 模型的概述2.ARMA 模型的数学表达式3.ARMA 模型的应用正文：一、ARMA 模型的概述自回归滑动平均模型（ARMA）是一种常用的时间序列分析方法，主要用于拟合和预测具有线性趋势的时间序列数据。

ARMA 模型是由自回归模型（AR）和滑动平均模型（MA）组合而成的，可以同时对时间序列数据中的长期依赖关系和短期依赖关系进行建模。

二、ARMA 模型的数学表达式ARMA 模型的数学表达式分为两个部分：自回归部分（AR）和滑动平均部分（MA）。

1.自回归部分（AR）自回归模型主要描述时间序列数据中的长期依赖关系，其数学表达式为：X_t = c + Φ1X_{t-1} + Φ2X_{t-2} +...+ ΦpX_{t-p} + ε_t其中，X_t 表示时间序列数据在t 时刻的取值，c 为常数项，Φ1、Φ2、...、Φp 为自回归系数，ε_t 为误差项。

2.滑动平均部分（MA）滑动平均模型主要描述时间序列数据中的短期依赖关系，其数学表达式为：X_t = μ+ θ1ε_{t-1} + θ2ε_{t-2} +...+ θqε_{t-q}其中，X_t 表示时间序列数据在t 时刻的取值，μ为常数项，θ1、θ2、...、θq 为滑动平均系数，ε_{t-1}、ε_{t-2}、...、ε_{t-q}为误差项。

将自回归部分和滑动平均部分相结合，即可得到ARMA 模型的数学表达式：X_t = c + Φ1X_{t-1} + Φ2X_{t-2} +...+ ΦpX_{t-p} + μ+ θ1ε_{t-1} + θ2ε_{t-2} +...+ θqε_{t-q}其中，c、μ为常数项，Φ1、Φ2、...、Φp、θ1、θ2、...、θq 分别为自回归系数和滑动平均系数，ε_t、ε_{t-1}、ε_{t-2}、...、ε_{t-q}为误差项。

三、ARMA 模型的应用ARMA 模型广泛应用于金融、经济学、气象学等领域的时间序列数据分析和预测。

ARMA模型基本架构及应用ARMA模型是一种经济时间序列分析方法，可以用于预测未来值的变动趋势。

ARMA模型基于两个组成部分，即自回归（AR）和移动平均（MA）。

自回归模型使用时间序列的过去值作为预测未来值的因素，而移动平均模型则使用时间序列的随机波动作为预测的基础。

Yt=c+φ1Yt-1+φ2Yt-2+…+φpYt-p+θ1εt-1+θ2εt-2+…+θqεt-q+εt在这个公式中，Yt表示时间序列的当前值，p表示自回归模型的阶数，q表示移动平均模型的阶数，c是一个常数，εt是一个随机扰动项。

AR部分表示时间序列变量的当前值与过去p个时间点的值之间的关系。

自回归模型常常用于表示时间序列存在的自相关性，即过去值对未来值的影响。

MA部分表示时间序列的当前值与过去q个随机波动的关系。

移动平均模型用于表示时间序列的随机性。

ARMA模型的应用非常广泛。

在经济学中，ARMA模型常用于分析股票价格、就业率、通货膨胀率等经济指标的时间序列数据。

通过建立ARMA模型，可以揭示时间序列数据中的规律和趋势，从而为决策提供有价值的信息。

ARMA模型还可以用于信号处理、气象预测、环境监测等领域。

例如，在信号处理中，ARMA模型可以用于预测随机信号的未来走势，以便进行故障检测和预防。

在气象预测中，ARMA模型可以用于预测未来一段时间内的气温、降雨量等天气指标。

除了ARMA模型，还有ARIMA模型、GARCH模型等时间序列分析方法，它们在处理特定的时间序列数据时具有一定的优势。

ARMA模型是这些方法中最简单和最基础的一种，但在实际应用中已经证明了其有效性和实用性。

总之，ARMA模型是一种用于分析时间序列数据的方法，可以用于预测未来值的变动趋势。

该模型采用了自回归和移动平均的思想，通过估计参数来确定时间序列数据中的规律和趋势。

ARMA模型在经济学、信号处理、气象预测等领域有广泛的应用，并且被证明是一种有效和实用的分析工具。

ARMA模型1.简单介绍ARMA模型是一类常用的随机时间序列预测模型，是一种精度较高的时间序列短期预测方法，它的基本思想是：某些时间序列是依赖于时间t的一族随机变量，构成该时间序列的单个序列值虽然具有不确定性，但整个序列的变化却有一定规律性，可用数学模型近似描述。

2.分类ARMA模型具有三种基本类型：自回归(AR)模型，移动平均（MA）模型，自回归移动平均（ARMA）模型。

3.表达如果时间序列是它的前期值和随机项的线性函数，即表示为：就称为P阶自回归模型，记为AR（p）。

其中称为自回归系数，是待估参数。

随机项是相互独立的白噪声序列，服从均值为0，方差为的正态分布。

且一般假定的均值也为0。

AR模型的平稳性问题从数学表达式来看，我们首先记为k步滞后算子，即。

则上述模型可写为：我们令（），模型就被简化为。

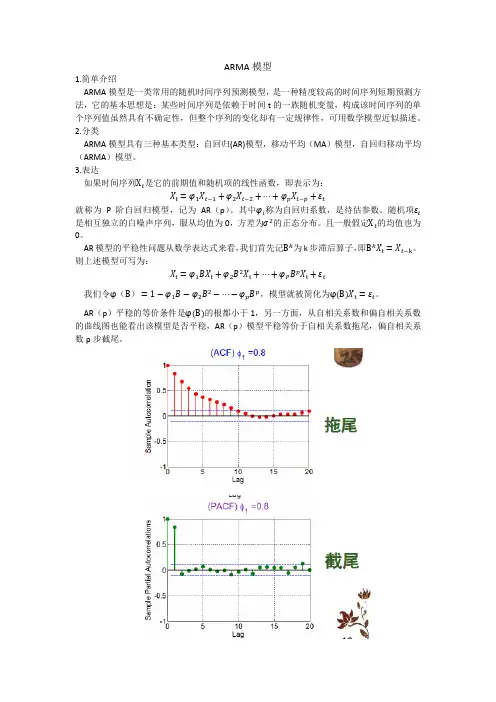
AR（p）平稳的等价条件是的根都小于1，另一方面，从自相关系数和偏自相关系数的曲线图也能看出该模型是否平稳，AR（p）模型平稳等价于自相关系数拖尾，偏自相关系数p步截尾。

而如果时间序列是它的当期和前期的随机误差项的线性函数，即则称为q阶移动平均模型，记为MA(q)。

它是无条件平稳的，因为它的均值和方差均为常数，跟AR模型做同样的滞后和简化，如果的根都小于1，则MA模型是可逆的。

另一个可逆的等价条件就是自相关函数q步截尾，偏自相关函数拖尾。

基于此，ARMA（p,q）模型的数学表达就呼之欲出了：而ARMA（p,q）的平稳条件就是AR(p)的平稳条件，可逆条件就是MA（q）的可逆条件。

而关于ARMA，它的自相关函数和偏自相关函数都是拖尾的。

4.代入本题之前在问题分析中也介绍了，我们将日期统一化，以第一次发生地震的日期作单位1参考，将数据集中的地震发生时间转化成了一个时间序列。

如图ts所示，我们分析了这组时间序列发现它的一阶差分是平稳的。

由上图，可看出它的一阶差分后的自相关函数和偏自相关函数都是拖尾的，故我们选择了ARMA(1,1)模型来做数据分析拟合。

自回归滑动平均模型（ARMA 模型，Auto-Regressive and Moving Average Model）是研究时间序列的重要方法，由自回归模型（简称AR模型）与滑动平均模型（简称MA模型）为基础“混合”构成。

在市场研究中常用于长期追踪资料的研究，如：Panel研究中，用于消费行为模式变迁研究；在零售研究中，用于具有季节变动特征的销售量、市场规模的预测等。

定义ARMA模型(auto regressive moving average model)自回归滑动平均模型，模型参量法高分辨率谱分析方法之一。

这种方法是研究平稳随机过程有理谱的典型方法，适用于很大一类实际问题。

它比AR模型法与MA模型法有较精确的谱估计及较优良的谱分辨率性能，但其参数估算比较繁琐。

ARMA模型参数估计的方法很多：如果模型的输入序列{u(n)}与输出序列{a(n)}均能被测量时，则可以用最小二乘法估计其模型参数，这种估计是线性估计，模型参数能以足够的精度估计出来；许多谱估计中，仅能得到模型的输出序列{x(n）}，这时，参数估计是非线性的，难以求得ARMA 模型参数的准确估值。

从理论上推出了一些ARMA模型参数的最佳估计方法，但它们存在计算量大和不能保证收敛的缺点。

因此工程上提出次最佳方法，即分别估计AR和MA参数，而不像最佳参数估计中那样同时估计AR和MA参数，从而使计算量大大减少。

基本原理将预测指标随时间推移而形成的数据序列看作是一个随机序列，这组随机变量所具有的依存关系体现着原始数据在时间上的延续性。

一方面，影响因素的影响，另一方面，又有自身变动规律，假定影响因素为x1，x2，…，xk，由回归分析，其中Y是预测对象的观测值，Z为误差。

作为预测对象Yt受到自身变化的影响，其规律可由下式体现，误差项在不同时期具有依存关系，由下式表示，由此，获得ARMA模型表达式：基本形式ARMA模型分为以下三种：自回归模型（AR：Auto-regressive）如果时间序列满足其中是独立同分布的随机变量序列，且满足：以及E() = 0则称时间序列为服从p阶的自回归模型。

ARMA模型介绍ARMA模型（Autoregressive Moving Average model）是时间序列分析中常用的一种模型，用于描述和预测随时间变化的数据。

ARMA模型结合了自回归（AR）和移动平均（MA）两种模型的特点，可以较好地描述时间序列数据的变化趋势。

ARMA模型的核心思想是：当前时刻的观测值可以通过历史观测值和随机误差的线性组合来表示。

具体地说，AR部分考虑了当前时刻和过去几个时刻的观测值之间的关系，而MA部分则考虑了当前时刻和过去几个时刻的随机误差之间的关系。

在AR模型中，当前时刻的观测值与过去几个时刻的观测值之间存在线性关系。

AR模型的阶数(p)表示过去几个时刻的观测值被考虑进来。

对于AR(p)模型，数学表达式如下：yt = c + φ1 * yt-1 + φ2 * yt-2 + ... + φp * yt-p + et其中，yt表示当前时刻的观测值，c表示常数项，φ1, φ2, ... ,φp表示对应的回归系数，et表示当前时刻的随机误差。

在MA模型中，当前时刻的观测值与过去几个时刻的随机误差之间存在线性关系。

MA模型的阶数(q)表示过去几个时刻的随机误差被考虑进来。

对于MA(q)模型，数学表达式如下：yt = c + et + θ1 * et-1 + θ2 * et-2 + ... + θq * et-q其中，yt表示当前时刻的观测值，c表示常数项，θ1, θ2, ... ,θq表示对应的回归系数，et表示当前时刻的随机误差。

yt = c + φ1 * yt-1 + φ2 * yt-2 + ... + φp * yt-p + et + θ1 * et-1 + θ2 * et-2 + ... + θq * et-qARMA模型可以用于时间序列的拟合和预测。

通过将模型与已有数据进行拟合，可以得到模型的参数估计值。

然后，利用这些参数估计值，可以预测未来的观测值。

ARMA模型适用于没有明显趋势和季节性的时间序列数据。

如何建立ARMA和ARMA模型如何进行模型的拟合与选择如何建立ARMA模型及进行模型的拟合与选择ARMA模型（自回归滑动平均模型）是一种常用的时间序列模型，可以帮助我们对数据进行预测和分析。

本文将介绍如何建立ARMA模型以及进行模型的拟合与选择。

一、ARMA模型的介绍ARMA模型是一种线性平稳时间序列模型，由自回归部分（AR）和滑动平均部分（MA）组成。

AR部分使用过去时间点的观测值作为自变量进行预测，MA部分使用过去时间点的误差项作为自变量进行预测。

ARMA模型的最一般形式为ARMA(p, q)，其中p代表AR部分的阶数，q代表MA部分的阶数。

二、建立ARMA模型的步骤1. 检验时间序列的平稳性ARMA模型要求时间序列是平稳的，即均值和方差保持不变。

可以通过绘制时间序列的图形、计算移动平均和自相关函数等方法来检验平稳性。

若发现非平稳性，则需要进行差分处理，直到得到平稳序列。

2. 确定模型的阶数通过观察自相关图（ACF）和偏自相关图（PACF），可以确定AR部分和MA部分的阶数。

ACF反映了序列与其滞后之间的关系，PACF则消除了中间滞后的干扰，更准确地显示滞后与序列之间的关系。

根据图形上截尾的特点，可以确定合适的阶数。

3. 估计模型参数利用最大似然估计或解方程组等方法，对ARMA模型进行参数估计。

最大似然估计是大多数情况下的首选方法，它通过最大化样本的对数似然函数，寻找最适合数据的参数估计值。

4. 模型检验和诊断对估计得到的模型进行检验和诊断，主要包括残差的自相关性检验、白噪声检验、模型拟合优度检验等。

如果模型不符合要求，需要重新调整模型的阶数或其他参数。

三、模型拟合与选择的方法1. 拟合优度准则模型的拟合优度准则可以用来衡量模型的优劣程度。

常见的拟合优度准则包括AIC（赤池信息准则）、BIC（贝叶斯信息准则）等。

这些准则基于模型的似然函数和模型参数的数量，从而在模型选择时提供一个客观的评估指标。

自回归移动平均模型公式
自回归移动平均模型（ARMA）是一种经济时间序列分析方法，用于预测未来的观测值。

它结合了自回归模型（AR）和移动平均模型（MA）的特点，具有很好的预测性能。

ARMA模型的数学表达式为：
y_t = c + φ₁*y_(t-1) + φ₂*y_(t-2) + ... + φ_p*y_(t-p) + ε_t + θ₁*ε_(t-1) +
θ₂*ε_(t-2) + ... + θ_q*ε_(t-q)
其中，y_t 是时间 t 的观测值，c 是常数项，φ₁, φ₂, ..., φ_p 是自回归系数，表示 t-1, t-2, ..., t-p 时刻 y 值对 t 时刻 y 值的线性影响；ε_t 是时间 t 的误差项，θ₁, θ₂, ..., θ_q 是移动平均系数，表示 t-1, t-2, ..., t-q 时刻的误差对 t 时刻 y 值的影响。

ARMA模型的参数估计可以利用最大似然估计或最小二乘法等方法进行。

根据观测数据的特征，选择合适的 AR 和 MA 阶数是模型建立的关键。

ARMA模型的预测能力在实际应用中被广泛认可。

通过估计模型参数，可以利用过去的观测值来预测未来的观测值。

预测结果可以帮助决策者制定相应的策略和措施。

需要注意的是，ARMA模型在实际应用中可能面临一些限制。

例如，如果数据存在非平稳性或季节性等特征，需要对数据进行预处理或使用其他模型进行分析。

总之，自回归移动平均模型是一种常用的时间序列分析工具，通过结合自回归和移动平均的特点，提供了对未来观测值的预测能力。

在实际应用中，应根据数据特征选择合适的阶数，并结合其他方法进行验证和优化，以达到更好的预测效果。

ARMA算法整理ARMA（自回归移动平均模型）算法是时间序列分析中经典的预测模型之一，它通过分析和拟合时间序列数据的自回归和移动平均部分，来预测未来的观测值。

ARMA算法整理如下。

1.自回归模型自回归模型是根据过去观测值的线性组合来预测未来观测值。

AR(p)模型中的p表示模型中包含p个滞后项，模型的公式如下：Y_t=c+Σ(φ_i*Y_t-i)+ε_t其中，Y_t是时间序列的观测值，c是常数，φ_i是自回归系数，ε_t是误差项。

2.移动平均模型移动平均模型是根据过去观测值的线性组合来预测未来观测值，与自回归模型不同的是，移动平均模型使用的是滞后项的误差项的线性组合。

MA(q)模型中的q表示模型中包含q个滞后误差项，模型的公式如下：Y_t=μ+Σ(θ_i*ε_t-i)+ε_t其中，Y_t是时间序列的观测值，μ是常数，θ_i是移动平均系数，ε_t是误差项。

3.自回归移动平均模型自回归移动平均模型（ARMA）是自回归模型和移动平均模型的结合，它同时利用了过去观测值和滞后误差项来预测未来观测值。

ARMA(p,q)模型中，p表示自回归模型中的滞后项数，q表示移动平均模型中的滞后误差项数，模型的公式如下：Y_t=c+Σ(φ_i*Y_t-i)+Σ(θ_i*ε_t-i)+ε_t其中，Y_t是时间序列的观测值，c是常数，φ_i是自回归系数，θ_i是移动平均系数，ε_t是误差项。

4.参数估计与模型识别ARMA模型的参数估计可以通过最大似然法或最小二乘法来进行。

而模型的选择和识别可以通过观察ACF（自相关函数）和PACF（偏自相关函数）的表现来进行，通常，ACF截尾于一些延迟阶数p，而PACF截尾于一些延迟阶数q，这时可以选择ARMA(p,q)模型。

5.模型拟合与预测一旦选择了合适的ARMA模型，可以对时间序列数据进行模型拟合和预测。

拟合过程中会估计出模型的参数，然后使用估计的参数进行预测。

预测的结果可以用于短期预测和长期趋势分析。

matlab自回归移动平均模型Matlab自回归移动平均模型（ARMA）是一种常用的时间序列分析方法，用于预测和建模具有自相关和移动平均特征的数据。

ARMA 模型结合了自回归（AR）模型和移动平均（MA）模型的特点，能够较好地拟合和预测时间序列数据。

ARMA模型的基本思想是通过线性组合当前时刻及过去时刻的观测值来预测未来时刻的观测值。

自回归模型（AR）假设未来时刻的观测值与过去时刻的观测值相关，即当前时刻的观测值可以由过去时刻的观测值线性组合得到。

移动平均模型（MA）则假设未来时刻的观测值与当前时刻及过去时刻的随机误差相关，即当前时刻的观测值可以由当前时刻及过去时刻的随机误差线性组合得到。

ARMA模型的数学表示可以用以下公式表示：y(t) = c + Σφ(i)y(t-i) + Σθ(j)e(t-j)其中，y(t)表示当前时刻的观测值，c表示常数项，φ(i)表示自回归系数，e(t)表示当前时刻的随机误差，θ(j)表示移动平均系数。

在Matlab中，可以使用arima函数来拟合和预测ARMA模型。

首先，需要提供时间序列数据，然后根据数据的特点选择合适的AR 和MA阶数，通过最小化模型的残差平方和来估计模型的参数。

最后，可以利用已估计的模型参数进行预测。

下面通过一个实例来演示如何在Matlab中使用ARMA模型进行时间序列分析。

假设我们有一段长度为100的时间序列数据，我们希望利用ARMA 模型来预测未来10个时刻的观测值。

首先，我们需要加载数据并进行可视化。

```matlabdata = randn(100,1); % 生成100个服从标准正态分布的随机数plot(data);xlabel('Time');ylabel('Value');title('Time Series Data');```接下来，我们可以使用arima函数拟合ARMA模型，并进行预测。

ARMA模型与ARIMA模型的推导与应用ARMA模型（AutoRegressive Moving Average model）和ARIMA模型（AutoRegressive Integrated Moving Average model）是一种常用的时间序列分析方法。

本文将对这两个模型进行推导，并探讨它们在实际应用中的作用。

一、ARMA模型的推导ARMA模型是一种线性预测模型，它由两部分组成：自回归部分（AR）和移动平均部分（MA）。

1. 自回归部分（AR）自回归部分是指当前序列的值与前一时刻的值之间存在线性关系，记作AR(p)。

其中p表示自回归阶数，即前p个时刻的值对当前值的影响。

假设当前时刻的值为yt，则AR(p)模型的表示为：yt = c + φ1*yt-1 + φ2*yt-2 + ... + φp*yt-p + εt其中，c为常数项，φ1, φ2, ..., φp为自回归系数，εt为误差项。

2. 移动平均部分（MA）移动平均部分是指当前序列的值与前一时刻的误差之间存在线性关系，记作MA(q)。

其中q表示移动平均阶数，即前q个时刻的误差对当前值的影响。

假设当前时刻的误差为et，则MA(q)模型的表示为：yt = c + θ1*et-1 + θ2*et-2 + ... + θq*et-q其中，c为常数项，θ1, θ2, ..., θq为移动平均系数。

二、ARIMA模型的推导ARIMA模型是在ARMA模型的基础上加入差分操作，以处理非平稳时间序列。

ARIMA模型由三部分组成：自回归部分（AR）、差分部分（I）和移动平均部分（MA）。

1. 自回归部分（AR）自回归部分与ARMA模型中的自回归部分相同，表示为AR(p)。

2. 差分部分（I）差分部分用于处理非平稳时间序列。

一阶差分操作即将当前值与前一时刻的值相减，次阶差分操作则再次对差分后的序列进行差分。

一般记作d阶差分，其中d表示差分阶数。

3. 移动平均部分（MA）移动平均部分与ARMA模型中的移动平均部分相同，表示为MA(q)。

马尔可夫区制转移arma模型马尔可夫区制转移(ARMA)模型是一种经济和金融时间序列分析常用的模型。

它的基本思想是通过分析当前时间点和过去时间点的关系，来预测未来时间点的值。

ARMA模型的构建基于两个关键概念：自回归(AR)和移动平均(MA)。

马尔可夫区制转移(AR)模型通过分析过去时间点对当前时间点的影响来预测未来时间点。

它基于一个假设，即未来的值是过去值的线性组合。

如果我们用Y表示时间序列的观测值，AR模型可以表示为：Y_t = c + φ_1 * Y_t-1 + φ_2 * Y_t-2 + ... + φ_p * Y_t-p + ε_t其中，Y_t是时间点t的观测值，c是常数，φ_1, φ_2, ...,φ_p是参数，p是模型的延迟数量，ε_t是误差项。

当p等于1时，AR模型称为AR(1)模型；当p等于2时，AR模型称为AR(2)模型，依此类推。

移动平均(MA)模型是用来描述观测值与白噪声误差项的线性组合之间的关系。

MA模型的基本假设是，当前时间点的观测值是过去时间点的误差项的线性组合。

如果我们用Y表示时间序列的观测值，MA模型可以表示为：Y_t = μ + ε_t + θ_1 * ε_t-1 + θ_2 * ε_t-2 + ... +θ_q * ε_t-q其中，Y_t是时间点t的观测值，μ是均值，ε_t是误差项，θ_1, θ_2, ..., θ_q是参数，q是误差项的延迟数量。

当q等于1时，MA模型称为MA(1)模型；当q等于2时，MA模型称为MA(2)模型，依此类推。

ARMA模型将AR和MA模型结合起来。

ARMA(p, q)模型可以表示为：Y_t = c + φ_1 * Y_t-1 + φ_2 * Y_t-2 + ... + φ_p * Y_t-p + ε_t + θ_1 * ε_t-1 + θ_2 * ε_t-2 + ... + θ_q * ε_t-qARMA模型可以通过最小二乘法或极大似然法来估计参数。

Arma模型通俗理解什么是ARMA模型？ARMA模型是时间序列分析中的一种建模方法，它是自回归移动平均模型（ARMA）的组合。

ARMA模型结合了自己的历史数据和随机误差来预测未来的数值。

AR和MA模型的概念在理解ARMA模型之前，我们需要先了解自回归（AR）和移动平均（MA）模型。

自回归（AR）模型自回归模型基于历史数据的线性组合来预测未来的数值。

它假设未来的值是过去值的加权和，其中权重由自回归系数确定。

自回归模型的公式为：x(t) = c + φ1 * x(t-1) + φ2 * x(t-2) + … + φp * x(t-p) + ε(t)，其中φ1, φ2, …, φp为自回归系数，ε(t)为误差项，c为常数。

移动平均（MA）模型移动平均模型基于随机误差的线性组合来预测未来的数值。

它假设未来的值是过去误差的加权和，其中权重由移动平均系数确定。

移动平均模型的公式为：x(t) = μ + θ1 * ε(t-1) + θ2 * ε(t-2) + … + θq * ε(t-q) + ε(t)，其中θ1,θ2, …, θq为移动平均系数，ε(t)为误差项，μ为均值。

ARMA模型ARMA模型是自回归模型和移动平均模型的结合，它综合了过去的数值和随机误差来预测未来的数值。

ARMA模型可以表示为ARMA(p, q)，其中p和q分别为自回归和移动平均阶数。

ARMA模型的公式为：x(t) = c + φ1 * x(t-1) + φ2 * x(t-2) + … + φp * x(t-p) + θ1 * ε(t-1) + θ2 * ε(t-2) + … + θq *ε(t-q) + ε(t)，其中φ1, φ2,…, φp为自回归系数，θ1, θ2, …, θq 为移动平均系数，c为常数，ε(t)为误差项。

如何估计ARMA模型的参数？ARMA模型的参数估计可以通过最小二乘法或最大似然法进行。

通过这些方法，可以找到使得模型拟合数据最好的参数。