矢量控制原理.ppt

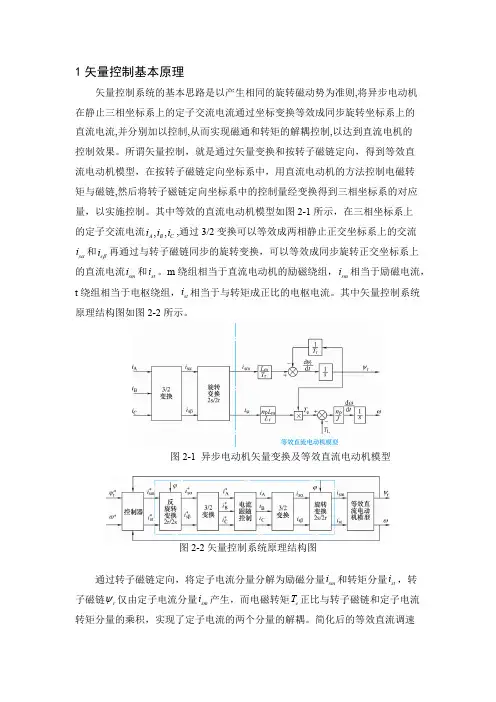
1矢量控制基本原理
矢量控制系统的基本思路是以产生相同的旋转磁动势为准则,将异步电动机在静止三相坐标系上的定子交流电流通过坐标变换等效成同步旋转坐标系上的直流电流,并分别加以控制,从而实现磁通和转矩的解耦控制,以达到直流电机的控制效果。

所谓矢量控制，就是通过矢量变换和按转子磁链定向，得到等效直流电动机模型，在按转子磁链定向坐标系中，用直流电动机的方法控制电磁转矩与磁链,然后将转子磁链定向坐标系中的控制量经变换得到三相坐标系的对应量，以实施控制。

其中等效的直流电动机模型如图2-1所示，在三相坐标系上的定子交流电流,通过3/2变换可以等效成两相静止正交坐标系上的交流,,A B C i i i 和再通过与转子磁链同步的旋转变换，可以等效成同步旋转正交坐标系上s i αs i β的直流电流和。

m 绕组相当于直流电动机的励磁绕组，相当于励磁电流，sm i st i sm i t 绕组相当于电枢绕组，相当于与转矩成正比的电枢电流。

其中矢量控制系统st i 原理结构图如图2-2所示。

图2-1 异步电动机矢量变换及等效直流电动机模型
图2-2矢量控制系统原理结构图
通过转子磁链定向，将定子电流分量分解为励磁分量和转矩分量，转sm i st i 子磁链仅由定子电流分量产生，而电磁转矩正比与转子磁链和定子电流r ψsm i e T 转矩分量的乘积，实现了定子电流的两个分量的解耦。

简化后的等效直流调速
系统如图2-3所示。

图4-2 带转矩内环和磁链闭环矢量控制系统的电气原理图
MATLAB 系统仿真系统设计
powergui A B
C +-
A
B C。

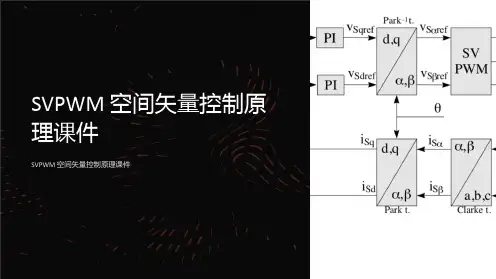
矢量控制(FOC）基本原理2０14、05、１5一、基本概念１、１模型等效原则交流电机三相对称得静止绕组 A 、Ｂ、C ,通以三相平衡得正弦电流时，所产生得合成磁动势就是旋转磁动势Ｆ，它在空间呈正弦分布,以同步转速ω1(即电流得角频率）顺着Ａ－B-C 得相序旋转。

这样得物理模型如图1－1a所示。

然而,旋转磁动势并不一定非要三相不可,单相除外,二相、三相、四相……等任意对称得多相绕组，通以平衡得多相电流,都能产生旋转磁动势,当然以两相最为简单。

图１图1-１b中绘出了两相静止绕组α与β，它们在空间互差90°,通以时间上互差９０°得两相平衡交流电流,也产生旋转磁动势F 。

再瞧图1－1ｃ中得两个互相垂直得绕组M 与 T，通以直流电流与,产生合成磁动势 F ，如果让包含两个绕组在内得整个铁心以同步转速旋转,则磁动势 F 自然也随之旋转起来,成为旋转磁动势。

把这个旋转磁动势得大小与转速也控制成与图 1-1ａ一样,那么这三套绕组就等效了。

三相－-两相变换(3S/2Ｓ变换）在三相静止绕组A、B、C 与两相静止绕组α、β之间得变换，简称３S/2S 变换。

其电流关系为两相—两相旋转变换（2Ｓ/2Ｒ变换)同步旋转坐标系中(Ｍ、T坐标系中）轴向电流分量与α、β坐标系中轴向电流分量得转换关系为１、2矢量控制简介矢量控制就是指“定子三相电流矢量控制”。

矢量控制理论最早为解决三相异步电机得调速问题而提出。

交流矢量得直流标量化可以使三相异步电机获得与直流电机一样优越得调速性能。

将交流矢量变换为两相直流标量得过程见图２。

图2图2得上图为静止坐标系下得定子三相交流矢量图2得中图为静止坐标系下得等效两相交流矢量图2得下图为旋转坐标系下得等效两相直流标量,就是转矩电流,就是励磁电流。

经图2得变换后,定子三相交流矢量变为了旋转得两相直流标量。

进而可以把异步电机瞧作直流电机,分别控制励磁电流与转矩电流。

变换公式即式(１)与式(2）。

矢量控制(FOC)基本原理一、基本概念1.1模型等效原则交流电机三相对称的静止绕组 A 、B 、C ，通以三相平衡的正弦电流时，所产生的合成磁动势是旋转磁动势F ，它在空间呈正弦分布，以同步转速ω1（即电流的角频率）顺着 A-B-C 的相序旋转。

这样的物理模型如图1-1a 所示。

然而，旋转磁动势并不一定非要三相不可，单相除外，二相、三相、四相…… 等任意对称的多相绕组，通以平衡的多相电流，都能产生旋转磁动势，当然以两相最为简单。

图1图1-1b 中绘出了两相静止绕组α 和 β ，它们在空间互差90°，通以时间上互差90°的两相平衡交流电流，也产生旋转磁动势F 。

再看图1-1c 中的两个互相垂直的绕组M 和 T ，通以直流电流M i 和T i ，产生合成磁动势F ，如果让包含两个绕组在内的整个铁心以同步转速旋转，则磁动势F 自然也随之旋转起来，成为旋转磁动势。

把这个旋转磁动势的大小和转速也控制成与图 1-1a 一样，那么这三套绕组就等效了。

三相--两相变换（3S/2S 变换）在三相静止绕组A 、B 、C 和两相静止绕组α、β之间的变换，简称3S/2S 变换。

其电流关系为111221022A B C i i i i i αβ⎡⎤⎡⎤--⎢⎥⎡⎤⎢⎥⎢=⎢⎥⎢⎥⎢⎣⎦⎢⎥-⎣⎦⎢⎦⎣（） 两相—两相旋转变换（2S/2R 变换） 同步旋转坐标系中（M 、T 坐标系中）轴向电流分量与α、β坐标系中轴向电流分量的转换关系为cos sin 2sin cos M T i i i i αβϕϕϕϕ⎡⎤⎡⎡⎤⎤=⎢⎥⎢⎢⎥⎥-⎦⎣⎦⎣⎣⎦ （）1.2矢量控制简介矢量控制是指“定子三相电流矢量控制”。

矢量控制理论最早为解决三相异步电机的调速问题而提出。

交流矢量的直流标量化可以使三相异步电机获得和直流电机一样优越的调速性能。

将交流矢量变换为两相直流标量的过程见图2。

图2图2的上图为静止坐标系下的定子三相交流矢量图2的中图为静止坐标系下的等效两相交流矢量图2的下图为旋转坐标系下的等效两相直流标量，T i 是转矩电流，M i 是励磁电流。

《矢量控制原理》矢量控制原理是一种电力电子技术，它使用矢量变换方法来实现对电机转子磁通和转子电流的精确控制。

这种控制方法可以提高电机的运行效率和精确度，使其在各种负载条件下都能稳定运行。

矢量控制原理主要是基于电磁学和电机理论，通过电流和磁场的控制来控制电机的转矩和速度。

其基本原理是通过控制电机定子上的电流分量和频率，产生一个旋转磁场，进而引起电机转子上的电流和磁场，从而形成一个旋转磁力矢量。

这种旋转磁力矢量可以根据实际需求，控制电机的速度、转矩和方向。

矢量控制原理的核心是矢量变换方法。

矢量变换是一种将三相电流或电压转换为以一个旋转矢量表示的方法。

在矢量变换中，三相正弦波电流或电压通过矢量变换公式，转换成旋转矢量的幅值和相位。

这种转换方式可以将三相电流或电压分解成它们的正弦波分量和余弦波分量，从而方便进行数学计算和控制。

在电机控制中，矢量控制原理主要应用在两种形式的控制中：转矩控制和转速控制。

转矩控制是指通过控制电机的定子电流或转子电流，来实现对电机输出转矩的精确控制。

转速控制是指通过控制电机的转子磁通和转子电流，来实现对电机转速的精确控制。

这两种控制方式在实际应用中经常结合使用，以实现对电机的全面控制。

矢量控制原理具有许多优点。

首先，它可以实现对电机的精确控制，使电机在不同负载条件下都能保持稳定的运行。

其次，它能够提高电机的运行效率，减少能量损失。

此外，矢量控制原理还能够实现对电机的快速响应和高动态性能，适应各种控制要求。

然而，矢量控制原理也存在一些局限性。

首先，它在控制电机过程中需要对电机的参数进行准确的测量和估计，才能实现准确的控制。

其次，矢量控制原理通常使用复杂的计算方法和算法，需要较高的计算能力和控制器硬件。

此外，矢量控制原理的实施和调试也需要一定的技术经验和专业知识。

总的来说，矢量控制原理是一种先进的电力电子控制技术，对电机的控制精度和效率有很大的提升。

随着电力电子技术和控制算法的进一步发展，矢量控制原理在电机控制领域的应用前景将更加广阔。

矢量控制系统(FOC)基本原理
矢量控制(FOC)基本原理
2022.05.15
duquqiubai1234163.
一、基本概念
1.1模型等效原则
交流电机三相对称的静止绕组A 、B 、C ，通以三相平衡的正弦电流时，所产生的合成磁动势是旋转磁动势 F ，它在空间呈正弦分布，以同步转速ω1（即电流的角频率）顺着A-B-C 的相序旋转。

这样的物理模型如图1-1a 所示。

然而，旋转磁动势并不一定非要三相不可，单相除外，二相、三相、四相…… 等任意对称的多相绕组，通以平衡的多相电流，都能产生旋转磁动势，当然以两相最为简单。

图1
图1-1b 中绘出了两相静止绕组α 和β ，它们在空间互差90°，通以时间上互差90°的两相平衡交流电流，也产生旋转磁动势F 。

再看图1-1c 中的两个互相垂直的绕组M 和T ，通以直流电流M i 和T i ，产生合成磁动势 F ，如果让包含两个绕组在的整个铁心以同步转速旋转，则磁动势 F 自然也随之旋转起来，成为旋转磁动势。

把这个
旋转磁动势的大小和转速也控制成与图1-1a 一样，那么这三套绕组就等效了。