计量经济学 李子奈版例题eviews数据
- 格式:xls
- 大小:127.00 KB
- 文档页数:1

计量作业计量经济学第
三版李子奈
文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]
计量经济学第三版李子柰
12 下表是中国内地2007年各地区税收Y和国内生产总值GDP的统计资料。
单位:(亿元)
Y GDP
3357065
594
625
434
9200
88
629
要求,以手工和运用Eviews软件(或其它软件):
(1)做出散点图,建立税收随国内生产总值GDP变化的一元线性回归方程,并解释斜率的经济意义;
(2)对所建立的回归方程进行检验;
(3)若2008年某地区国内生产总值为8500亿元,求该地区税收入的预测值机预测区间。
解:下图是运用Eviews软件分析出的结果。
Dependent Variable: Y
Method: Least Squares
Date: 09/17/11 Time: 15:13
Sample: 2 32
Included observations: 31
Variable Coefficient Std. Error t-Statistic Prob.
GDP
Adjusted R-squared . dependent var
. of regression Akaike info criterion
Sum squared resid 2760310. Schwarz criterion
Log likelihood F-statistic
Durbin-Watson stat Prob(F-statistic)。

2.8:散点图:graph01。
建立一元线性回归模型。
参数估计:eq02。
可得出模型:t t x y 69.031.135+=预测:graph02。
得到1990年、2000年某城镇居民年人均消费性支出预测值为:1354.89、1424.05.3.7进行回归分析,建立回归模型。
1用最小二乘法做参数估计:eq02/stats 。
得到回归方程:i i i x x y 219117.00494.05398.158-+=。
回归标准差为:20.217572经济意义检验:可得出所有的回归系数的符号和大小都与经济理论及人们的经验期望值相一致。
3统计检验:(1) 拟合优度检验:得出样本回归方程较好的拟合了样本观测值。
(2) F 检验:F=72.9065>4.46,所以回归方程是显著的.(3) t 检验:t1=10.5479>2.306即1β显著不等于0;9213.02-=t <2.306不能否定02=β即x2不能作为解释变量进入模型.4预测eq02/resids在2000年我国城镇居民家庭人均可支配收入为5800,耐用消费价格指数为135,进行预测可得2000Y 的置信度为0.95的预测区间为(267.2001,376.7605)4.31对CES 函数进行线性化处理,再用最小二乘法做参数估计:eq02/stats.得出回归方程:2)]([0602.00293.11693.17145.8)(LK Ln LnL LnK LnGDP -++-=分别得到A m ,,ρδ的估计值A=0.00016、δ=0.5318、ρ=0.2199、m=2.1986.2 预测:eq02/resids最后得出CES 的生产函数为2199.01986.22199.02199.0]4682.05318.0[00016.0---+=L KGDP当2199.0=ρ时得出K 与L 的替代弹性8197.0=σ5.51建立计量经济模型i i i u X Y ++=10ββ用普通最小二乘法估计:eq03。

某财经学院李子奈《计量经济学》课程试卷(含答案)__________学年第___学期考试类型:(闭卷)考试考试时间:90 分钟年级专业_____________学号_____________ 姓名_____________1、判断题(3分,每题1分)1. 消除序列相关的一阶差分变换假定自相关系数ρ必须等于1。
()正确错误答案:正确解析:消除序列相关的一阶差分变换假定自相关系数ρ=1,即假设随机干扰项之间是完全正序列相关的,这样广义差分方程就转化为一阶差分方程。
2. 随机干扰项μi和残差项ei是一回事。
()正确错误答案:错误解析:随机干扰项是针对总体回归模型而言的,它是模型中其他没有包含的因素的综合体;而残差项是针对样本回归模型而言的,它是实际观测值与样本回归线上值的离差。
两者的含义不同,后者只能说成是对前者的一个估计。
3. 在C-D生产函数Y=AKαLβ中,α和β分别是劳动与资本的产出弹性。
()正确错误答案:错误解析:在C-D生产函数Y=AKαLβ中,α和β分别是资本与劳动的产出弹性。
2、名词题(5分,每题5分)1. 总体回归函数答案:总体回归函数是指在给定量下Y,分布的总体均值与X所形成的函数关系(或者说将总体被解释变量的条件期望表示为解释变量的某种函数)。
由于变量间关系的随机性,回归分析关心的是根据解释变量的已知或给定值,考察被解释变量的总体均值,即当解释变量取某个确定值时,与之统计相关的被解释变量所有可能出现的对应值的平均值。
解析:空3、简答题(25分,每题5分)1. 表3-1列出了某地区家庭人均鸡肉年消费量Y,与家庭月平均收入X,鸡肉价格P1,猪肉价格P2与牛肉价格P3的相关数据。
表3-1(1)求出该地区关于家庭鸡肉消费需求的如下模型:lnY=β0+β1lnX+β2lnP1+β2lnP2+β3lnP3+μ(2)请分析,鸡肉的家庭消费需求是否受猪肉及牛肉价格的影响?答案:(1)Eviews软件的回归结果如图3-1所示。

李子奈《计量经济学》课后习题详解(非经典截面数据计量经济学模型)【圣才出品】第6章非经典截面数据计量经济学模型1.在经典截面数据计量经济学模型中,通常选择哪些类型的数据作为样本数据?对被解释变量样本数据有哪些假定?答:(1)在经典的截面数据计量经济学模型中,通常选择横截面数据作为样本数据。
(2)对被解释变量的样本数据,通常有以下假定:①假定被解释变量都是连续型的随机抽取的变量;②假定被解释变量和随机干扰项所服从的分布类型是一致的;③假定得到的被解释变量的样本观测值可以完全反映被解释变量的实际状态。
2.某一截面数据计量经济学模型Y i=β′X i+μi,被解释变量服从正态分布,其样本观测值为Y1,Y2,…,Y n,其中Y1,Y2,Y3取相同的值α,其他观测值均大于α。
分别将该组样本看作未受限制的随机抽取样本、以α为截断点的选择性样本、以α为归并点的选择性样本,分别采用最大似然法估计模型。
(1)写出3种情况下的对数似然函数表达式。
(2)比较3种情况下对数似然函数值的大小,并加以简单证明。
解:(1)①在假设该组样本为未受限制的随机抽样样本时,其似然函数为:()()()()()()()223222141221/212/21,,,,212ii ni i i i i Y X n n na X Y X n nL P Y Y Y eeβσββσβσπσπσ==--??--+-∑∑∑===对该似然函数方程的左右两边分别取对数,可得其对数似然函数表达式为:()()()32222141ln ln 222ni i i i i n L a X Y X πσββσ==??=---+-??∑∑②当假设所取的样本为以α为截断点的选择性样本时,其似然函数为:()()224431ln ln 2ln 122nni iii i a X n L YX βπσβσσ==?-?-??=-----Φ?? ????∑∑③当假设所取的样本为以α为归并点的选择性样本时,Y i 的概率密度似然函数分为两部分为两部分,一部分是Y i =α的前三个点,其概率密度函数为:()()i i i i a X P Y P a X βαμβσ-??==≤-=Φ另一部分是后n -3个点,他们服从正态分布N (X i β,σ2),其概率密度函数为:()()2221i i Y X i f Y eβσ--=于是,当假设所取的样本为以α为归并点的选择性样本时,有如下似然函数:()()2322141,i i Y X ni i i a X L e βσββσσ-==??-??=∏Φ?∏相应的对数似然函数为:()()32224131ln ln 2ln 22ni iii i a X n L Y X βπσβσσ==--??=---+Φ ∑∑(2)①比较截断模型与归并模型的对数最大似然函数值。

154页第9题作业步骤:一、用OLS法建立模型第一步:建立WORKFILEFil e→ new →workfile→弹出对话框→选择dated-regular frequency→右边填起始时间1980-2007→OK第二步:输入数据1、建立存放数据的Group:在命令主出口输入命令DATA Y X然后按ENTER运行2、从原来保存数据的表格中复制数据到Group第三步:软件操作OLS法主命令窗口输入:LS log(Y) C log(X) 按ENTER运行注意:一定要看清楚模型的设定,到底哪个是自变量,哪个是因变量,变量的形式是如何的,比如是否取对数回归。
结果如图所示:普通最小二乘法的估计结果如下:.1=5885ln+.08544XY ln11.8459 60.0906(0.0000)(0.0000)R2=0.9929 D.W.=0.3793 F=3601.8785 RSS=0.3282 估计结果显示,lnY变化的99.29%可由lnX的变化来解释,模型拟合程度很好。
在1%的显著性水平下,lnX的参数显著,参数为0.8544,其经济意义表示全社会固定投资的对数增加1%,工业增加值的对数增加0.755%。
2、检验模型是否存在序列相关第一种方法:图示法第一步:求原来模型的参差项(e~的值)i只要对原来的模型进行普通最小二乘估计就可以求的残差项,残差项在系统中默认为resid.Resid的位置在workfile窗口,如下图所示。
第二步:生成随机干扰项序列E命令窗口输入:genr e=resid 然后按enter运行或者手动操作:workfile界面点genr →对话框输入:e=resid → ok第三步:画图1、画残差e与时间的图Quick→Graph→弹出对话框→输入year(横轴) →resid^2(纵轴) →OK→下拉菜单选 scatter diagram→ok (结果如下图)2、e和e(-1)的相关图操作:主界面点Quick → Graph →对话框输入:e(-1) e →ok →下拉菜单选Scatter Diagram → ok结果如下图所示:从上图可以看出残差的点大多数落在第一象限和第三象限,表明随机误差项存在正序列相关。
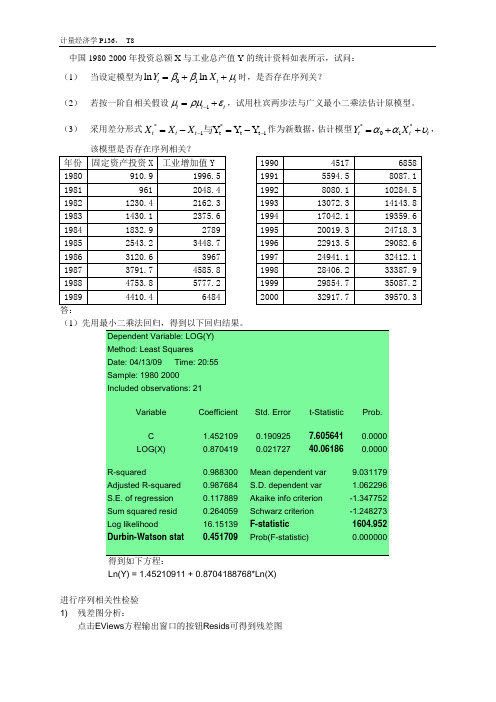
中国1980-2000年投资总额X 与工业总产值Y 的统计资料如表所示,试问: (1) 当设定模型为01ln ln t t t Y X ββμ=++时,是否存在序列关?(2) 若按一阶自相关假设1t t t μρμε-=+,试用杜宾两步法与广义最小二乘法估计原模型。
(3) 采用差分形式**1t t t 1Y Y Y t t t X X X --=-=-与作为新数据,估计模型**01t t t Y X ααυ=++,该模型是否存在序列相关?(1)先用最小二乘法回归,得到以下回归结果。
Dependent Variable: LOG(Y) Method: Least Squares Date: 04/13/09 Time: 20:55 Sample: 1980 2000 Included observations: 21Variable Coefficient Std. Error t-Statistic Prob.C 1.452109 0.190925 7.605641 0.0000 LOG(X)0.8704190.02172740.061860.0000R-squared0.988300 Mean dependent var 9.031179 Adjusted R-squared 0.987684 S.D. dependent var 1.062296 S.E. of regression 0.117889 Akaike info criterion -1.347752 Sum squared resid 0.264059 Schwarz criterion -1.248273 Log likelihood 16.15139 F-statistic 1604.952 Durbin-Watson stat0.451709 Prob(F-statistic)0.000000得到如下方程:Ln(Y) = 1.45210911 + 0.8704188768*Ln(X)进行序列相关性检验 1) 残差图分析:点击EViews 方程输出窗口的按钮Resids 可得到残差图在残差图中,残差的变动有系统模式,连续为正和连续为负,表明残差项存在正自相关,模型中t 统计量和F 统计量的结论不可信,需采取补救措施。
实验二 可化为线性的非线性回归模型估计、受约束回归检验及参数稳定性检验一 实验目的:(1)掌握可化为线性的非线性回归模型的估计方法; (2)模型参数的线性约束检验方法; (3)掌握Chow 检验的基本原理和主要用途;(4)掌握Chow 分割点检验和Chow 预测检验的操作过程,判断分割点。
二 实验要求:应用教材P83例子3.5.1做可化为线性的非线性回归模型估计,利剑受约束回归检验,掌握Chow 稳定性检验。
三 实验原理:普通最小二乘法、模型参数线性受约束检验法、Chow 检验法。
四 预备知识:最小二乘估计原理、t 检验、F 检验、Chow 检验。
五 实验内容:下表列出了中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y ,资产合计K 及职工人数L 。
Y Ak l eαβμ=(1)利用上述资料,进行回归分析。
(2)回答:中国概念的制造总体呈现规模报酬不变状态吗?六 实验步骤:建立工作文件并导入全部数据,如图 1所示 (1)设定并估计可化为线性的非线性回归模型:0lnY alnK lnL ββμ=+++在Eviews 软件下,点击主界面菜单Qucik/Estimate Equation ,在弹出的对话框中输入log(Y) C log(K) log(L),点击确定即可得到回归结果,如图2所示。
根据图2中的数据,得到模型的估计结果为:ln 1.15399 0.60924ln K 0.360807lnLY ∧=++(1.586) (3.454) (1.790)R 2=0.809925 2R =0.796348 D.W.=0.793209∑e i 2=5.070303 F=59.65501 df=(2,28)随机干扰项的方差估计值为:2ˆσ=()2i e /n 3∑-=5.070303/28=0.18108225 回归结果表明,这一年lnY 变化的81%可由lnK 和lnL 的变化来解释。
《计量经济学》实验报告实验一:EViews5.0软件安装及基本操作1.Eviews5.0的安装过程解压安装包,双击“Setup.exe”,选择安装路径进行安装;安装完毕后,复制“eviews5.0破解文件夹”下的“eviews5.reg文件”和“eviews5.exe文件”到安装目录下;双击“Eviews5.reg”进行注册,安装完毕。
2.基本操作(数据来源于李子奈版课后习题P61.12)运行Eviews,依次单击file→new→work file→unstructed→observation 31。
命令栏中输入“data y gdp”,打开“y gdp”表,接下来将数据输入其中。
做出“y gdp”的散点图,依次单击quick→graph→scatter→gdp y。
结果如下:开始进行LS回归:回归方程为:Y = -10.39340931 + 0.0710********GDP对回归方程做检验:斜率项t值9.59大于t在5%显著水平下的检验值2.045,拒绝零假设;截距项t 值0.121小于2.045,接受零假设。
可决系数0.76,拟合较好,方程F检验值91.99通过F检验。
下面进行预测:拓展工作空间:打开work file窗口,单击 Proc→Structure,将End date 的数据31→32;确定预测值的起止日期:打开work file窗口,点击Quick→Sample,填入“1 32”。
打开GDP数据表,在GDP的最下方填,按回车键。
在出现的Equation界面,点击Forecast出现相应界面如下:实验二:回归模型的建立与检验(数据来源于李子奈版课后习题P105.11)运行Eviews,依次单击file→new→work file→unstructed→observation 10。
命令栏中输入“data y x1 x2”,打开“y x1 x2”表,接下来将数据输入其中。
开始进行LS回归:估计方程:依次单击view→representations,得到回归方程为:Y = 626.5092847 - 9.790570097*X1 + 0.028*********X2,参数估计完毕。