福建泉州数学解析-2014初中毕业学业考试试卷

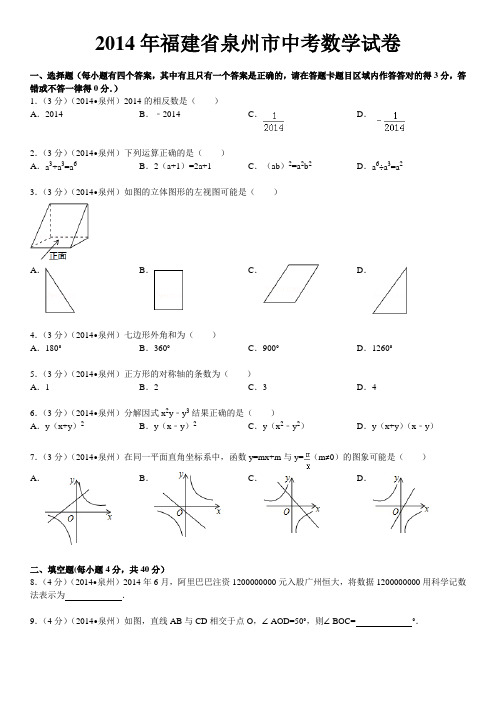
2014年福建省泉州市初中毕业、升学考试数 学 试 题（满分：150分；考试时间：120分钟）友情提示：所有答案必须填写到答题卡相应的位置上.毕业学校 姓名考生号一、选择题（每小题3分，共21分）：每小题有四个答案,其中有且只有一个答案是正确的．请在答题卡上相应题目的答题区域内作答,答对的得3分,答错或不答一律得0分． 1. 2014的相反数是（ ）．A. 2014B. 2014-C. 12014D. 12014- 2. 下列运算正确的是（ ）．A ．633a a a =+ B ．12)1(2+=+a a C ．222)(b a ab = D ．236a a a =÷3. 下列左图所示的立体图形的左视图．．．可能是（ ）．4. 七边形的外角和为（ ）．A ．︒180B ．︒360C ．︒900D ．︒1260 5．正方形的对称轴的条数为（ ）．A ．1B ．2C ．3D ．4 6. 分解因式32y y x -结果正确的是（ ）．A ． 2)(y x y +B ． 2)(y x y -C ． )(22y x y -D ． ))((y x y x y -+ 7. 在同一平面直角坐标系中，函数m mx y +=与)0(≠=m xmy 的图象可能是（ ）．（正面）A. B. C. D.A. B.C.D.二、填空题（每小题4分，共40分）：在答题卡上相应题目的答题区域内作答．8. 2014年6月份，阿里巴巴注资0000001200元入股广州恒大，将0000001200用科学计数法表示为__ _.9. 如图，直线AB 与CD 相交于点O ,︒=∠50AOD ,则=∠BOC °． 10．计算：12121m m m m ++=++ _____________．11．方程组⎩⎨⎧=+=-62,0y x y x 的解是_____________．12. 在综合实践课上，六名同学的作品数量（单位：件）分别为：3、5、2、5、5、7，则这组数据的众数为 件．13. 如图，直线a ∥b ，直线c 与直线a 、b 都相交，︒=∠651，则=∠2 °．14. 如图，ABC Rt ∆中，︒=∠90ACB ,点D 为斜边AB 的中点，10=AB cm ，则CD 的长为 cm ．15. 如图，在ABC ∆中，20C ∠=︒，CA CB =，则ABC ∆的外角ABD ∠＝ °．16. 已知m 、n为两个连续的整数，且m n <<，则m n += . 17. 如图所示，有一直径是2米的圆形铁皮,现从中剪出一个圆周角是︒90的最大扇形ABC .则(1)AB 的长为 米；(2)用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为 米.三、解答题（共89分）：在答题卡上相应题目的答题区域内作答． 18.（9分）计算：16486)132(10+⨯--+--． 19.（9分）先化简，再求值:)4()2(2-++a a a ，其中3=a ．20．（9分）已知:如图，在矩形ABCD 中,E 、F 分别在AB 、CD 边上，DF BE =，连结CE 、AF .求证：CE AF =.（第13题图）（第14题图）（第9题图）（第17题图）21.（9分）在一个不透明的箱子里，装有红、白、黑各一个．．．球，它们除了颜色之外没有其它区别． (1)随机地从箱子里取出1个球，则取出红球的概率是多少？(2)随机地从箱子里取出1个球，放回搅匀再取第二个球.请你用画树状图或列表的方法表示所有等可能的结果，并求两次取出相同颜色球的概率．22．（9分）如图,已知二次函数3)(2+-=h x a y 的图象经过原点)0,0(O 、)0,2(A . (1)直接写出该函数图象的对称轴；(2)若将线段OA 绕着点O 逆时针旋转60︒到'OA ，试判断点'A 是否 为该函数图象的顶点？23.（9分）课外阅读是提高学生素养的重要途径，某校为了了解学生课外阅读情况，随机抽查了50 名学生，统计他们平均每天课外阅读时间（t 小时），根据t 的长短分为A 、B 、C 、D 四类.下面是根据所抽查的人数绘制的两幅不完整的统计图表，请根据图中提供的信息，解答下面的问题：(1)求表格中的a 值，并在图中补全条形统计图；(2)该校现有1300名学生，请你估计该校共有多少学生课外阅读时间不少于．．．1小时？（第22题图）50名学生平均每天课外阅读时间统计表 50名学生平均每天课外阅读时间条形统计图 5A B C D 类别人数24.（9分）某学校开展“青少年科技创新比赛”活动，“喜羊羊”代表队设计了一个遥控车沿直线轨道AC 做匀速运动的模型．甲、乙车同时．．分别从A 、B 两处出发，沿轨道到达C 处，B 在AC 上．甲的速度是乙的5.1倍．设t （分）后甲、乙两遥控车与．B ．处．的距离．．．分别为1d 、2d （米），则1d 、2d 与t 的函数关系如图所示．试根据图象解决下列问题： (1)填空：乙的速度2v = 米/分； (2)求1d 与t 的函数关系式；(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰， 试探求什么时间两遥控车的信号不会产生相互干扰？25.（12分）如图,在锐角三角形纸片ABC 中, BC AC >,点D 、E 、F 分别在边AB 、BC 、CA 上. (1)已知:AC DE //,BC DF //. ①判断四边形DECF 一定是．．．什么形状； ②裁剪当cm AC 24=，cm BC 20=，45ACB ∠=o时，请你探索：如何剪四边形DECF ，能使它的面积最大，并证明你的结论； (2)折叠请你只用两次．．折叠，确定四边形的顶点D 、E 、C 、F ， 使它恰好．．为菱形，并说明你的折法和理由．（第24题图）)A（第25题图）BCDFEA（第25题备用图）B C26.（14分）如图，直线3+-=x y 与x 、y 轴分别交于点A 、B ，与反比例函数的图象交于点)1,2(P . (1)求该反比例函数的关系式；(2)设y PC ⊥轴于点C ，点A 关于y 轴对称点为'A . ①求BC A '∆的周长和C 'BA sin ∠的值；②对于大于1的常数m ,求x 轴上点M 的坐标，使得mBMC sin 1=∠.(以下空白作为草稿纸)（第26题图）2014年福建省泉州市初中毕业、升学考试数学试题参考答案及评分标准说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分． （二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分．（三）以下解答各行右端所注分数表示正确做完该步应得的累计分数． 一、选择题（每小题3分，共21分） 1．B 2．C 3．A 4．B 5． D 6．D 7．A 二、填空题（每小题4分，共40分）8．9102.1⨯ 9．50 10．1 11．⎩⎨⎧==2,2y x12．5 13．65 14．5 15．110 16．7 17．1； 41三、解答题（共89分）18.（本小题9分）解：原式=4261+-+=9 19．（本小题9分）解：原式=a a a a 44422-+++=422+a 当3=a 时，原式4)3(22+⨯=432+⨯= 10=20．（本小题9分）证明：在矩形ABCD 中,BC AD =,︒=∠=∠90B D ， ∵DF BE =，∴ADF ∆≌CBE ∆， ∴CE AF =. 21．（本小题9分） 解：（1）P (取出红球)31=； (2)方法一：画树状图如下：由树状图可知，共有9种机会均等的情况，其中两次取出相同颜色的球有3种情况，∴P (取出相同颜色的球)=13=. 红 白 黑 红 白 黑红 白 黑 红 白 黑第一次 第二次方法二：列表如下：由列表可知，共有9种机会均等的情况，其中两次取出相同颜色的球有3种情况， ∴P (取出相同颜色的球)=3193=. 22．（本小题9分） 解：（1）该函数图象的对称轴为直线1=x ；（2）由图形的旋转性质得：2'==OA OA ,︒=∠60'OA A ,过'A 作x B A ⊥'轴于B , ∴121260cos '=⨯=︒=OA OB ， 323260sin ''=⨯=︒=OA B A .∴)3,1('A 为该函数图象的顶点．23．（本小题9分） 解：（1）5，补全条形统计图如图所示：（2）52050201300=⨯（人）． 答：估计该校共有520名学生课外阅读时间不少于1小时．24．（本小题9分） 解：（1）40；（2）当10<≤t 时，60601+-=t d ；当31≤≤t 时，60601-=t d . （3）由题意可得：t d 402=,①当10<≤t 时,1021>+d d ，10406060>++-t t ,50名学生平均每天课外阅读时间条形统计图 05A B C D类别人数 （第22题图）∴5.2<t （分）； ∴10<≤t .② 当31≤≤t 时,1012>-d d ， 10)6060(40>--t t ， 5.2<t （分）， ∴5.21<≤t .综上,当5.20<≤t 时,两遥控车的信号不会产生相互干扰. 25．（本小题12分） 解：（1）①平行四边形；②设x FC =cm （240<<x ），则)24(x AF -=cm.过点F 作BC FH ⊥于点H , 则x x FH 2245sin =⋅=, ∵BC DF //,∴ADF ∆∽ABC ∆,∴ACAFBC DF =, ∴)24(6524)24(20x x DF -=-=, ∴FH FC S DECF ⋅=四边形 =x x 22)24(65⋅-=[]2212)12(2125+--x . ∴当12=x 时，四边形DECF 面积取得最大值为260, 此时AC FC 21=, 即沿三角形的中位线DF 、DE 剪四边形DECF ，能使它的面积最大.(2) 如图，先折ACB ∠的平分线（使CB 落在CA 上，压平），折痕与AB 的交点为D ；再折DC 的垂直平分线（使点C 与点D 重合，压平），折痕与BC 、CA 的交点分别为点E 、F ，展平后四边形CEDF 就是菱形.理由如下：由CB 落在CA 上，折线与AB 的交点为D 可得：ACD ∠=BCD ∠,由点C 与点D 重合，折线与BC 、CA 的交点分别为点E 、F ， 可得CE DE DF CF ===.A（第25题图1）BCDFE HA C （D ） E （F ）B即四边形CEDF 为菱形. 26．（本小题14分）解：（1）设反比例函数的关系式为)0(≠=k xky ,则2==xy k ， ∴反比例函数的关系式为xy 2=. （2）①由题意得：)0,3('-A )3,0(B ,)1,0(C ,则2=BC ,1=OC ，3'=O A ， ∴23'22'=+=OB O A B A ,10'22'+=OC O A C A ，∴BC A '∆的周长为10232++. 设C 到B A '的距离为h ，O A BC h B A ''2121⨯=⨯, ∴3223⨯=⨯h ，得2=h ，∴55102sin ''===∠C A h C BA . ②若点M 在x 轴的负半轴上，设ΔMCB 的外接圆的圆心为N ,半径为r ， 则点N 在BC 的中垂线ND 上，NM NC NB ==，则有BNC BND BMC ∠=∠=∠21， ∴BND BMC ∠=∠sin sin ,∴11=m r，即=r m . 过N 作x NE ⊥轴于点E ,则2=NE ，∴当21<<m 时，⊙N 与x 轴相离，点M 不存在，当2≥m 时，⊙N 与x 轴相交（或相切），12-==m ND OE ，42-=m ME ，∴4122-±-=±=m m ME OE OM ,故点M 的坐标为)0,41(22----m m 、)0,41(22-+--m m . 若点M 在x 轴的正半轴上，由图形的对称性同理可得：点M 的坐标为)0,41(22---m m 、)0,41(22-+-m m ； 综上所述，当21<<m 时，点M 不存在；当2≥m 时，点M 的坐标为)0,41(22----m m 、)0,41(22-+--m m 、)0,41(22---m m 、)0,41(22-+-m m .（第26题图1）（第26题图2）。

2014年福建省泉州市中考数学试卷学校:___________姓名：___________班级：___________考号：___________一、选择题(本大题共7小题，共21.0分)1.2014的相反数是（）A.2014B.-2014C.D.【答案】B【解析】解：2014的相反数是-2014．故选：B．根据只有符号不同的两个数互为相反数，可得一个数的相反数．本题考查了相反数的概念，在一个数的前面加上负号就是这个数的相反数．2.下列运算正确的是（）A.a3+a3=a6B.2（a+1）=2a+1C.（ab）2=a2b2D.a6÷a3=a2【答案】C【解析】解：A、a3+a3=2a3，故A选项错误；B、2（a+1）=2a+2≠2a+1，故B选项错误；C、（ab）2=a2b2，故C选项正确；D、a6÷a3=a3≠a2，故D选项错误．故选：C．根据二次根式的运算法则，乘法分配律，幂的乘方及同底数幂的除法法则判断．本题主要考查了二次根式的运算法则，乘法分配律，幂的乘方及同底数幂的除法法则，解题的关键是熟记法则运算3.如图的立体图形的左视图可能是（）A. B. C. D.【答案】A【解析】解：此立体图形的左视图是直角三角形，故选：A．左视图是从物体左面看，所得到的图形．本题考查了几何体的三种视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中．4.七边形外角和为（）A.180°B.360°C.900°D.1260°【答案】B【解析】解：七边形的外角和为360°．故选：B．根据多边形的外角和等于360度即可求解．本题考查了多边形的内角和外角的知识，属于基础题，掌握多边形的外角和等于360°是解题的关键．5.正方形的对称轴的条数为（）A.1B.2C.3D.4【答案】D【解析】解：正方形有4条对称轴．故选：D．根据正方形的对称性解答．本题考查了轴对称的性质，熟记正方形的对称性是解题的关键．6.分解因式x2y-y3结果正确的是（）A.y（x+y）2B.y（x-y）2C.y（x2-y2）D.y（x+y）（x-y）【答案】D【解析】解：x2y-y3=y（x2-y2）=y（x+y）（x-y）．故选：D．首先提取公因式y，进而利用平方差公式进行分解即可．此题主要考查了提取公因式法以及公式法分解因式，熟练应用平方差公式是解题关键．7.在同一平面直角坐标系中，函数y=mx+m与y=（m≠0）的图象可能是（）A. B. C. D.【答案】A【解析】解：A、由函数y=mx+m的图象可知m＞0，由函数y=的图象可知m＞0，故A选项正确；B、由函数y=mx+m的图象可知m＜0，由函数y=的图象可知m＞0，相矛盾，故B选项错误；C、由函数y=mx+m的图象y随x的增大而减小，则m＜0，而该直线与y轴交于正半轴，则m＞0，相矛盾，故C选项错误；D、由函数y=mx+m的图象y随x的增大而增大，则m＞0，而该直线与y轴交于负半轴，则m＜0，相矛盾，故D选项错误；故选：A．先根据一次函数的性质判断出m取值，再根据反比例函数的性质判断出m的取值，二者一致的即为正确答案．本题主要考查了反比例函数的图象性质和一次函数的图象性质，要掌握它们的性质才能灵活解题．二、填空题(本大题共10小题，共40.0分)8.2014年6月，阿里巴巴注资1200000000元入股广州恒大，将数据1200000000用科学记数法表示为______ ．【答案】1.2×109【解析】解：将1200000000用科学记数法表示为：1.2×109．故答案为：1.2×109．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．9.如图，直线AB与CD相交于点O，∠AOD=50°，则∠BOC=______ °．【答案】50【解析】解；∵∠BOC与∠AOD是对顶角，∴∠BOC=∠AOD=50°，故答案为：50．根据对顶角相等，可得答案．本题考查了对顶角与邻补角，对顶角相等是解题关键．10.计算：+= ______ ．【答案】1【解析】解：原式==1，故答案为：1．根据同分母分式相加，分母不变分子相加，可得答案．本题考查了分式的加减，同分母分式相加，分母不变分子相加．11.方程组的解是______ ．【答案】【解析】解：，①+②得：3x=6，即x=2，将x=2代入①得：y=2，则方程组的解为．故答案为：．方程组利用加减消元法求出解即可．此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．12.在综合实践课上，六名同学的作品数量（单位：件）分别为：3、5、2、5、5、7，则这组数据的众数为______ 件．【答案】5【解析】解：∵5出现了3次，出现的次数最多，∴这组数据的众数为5；故答案为：5．根据众数的定义即一组数据中出现次数最多的数，即可得出答案．此题考查了众数，众数是一组数据中出现次数最多的数，注意众数不止一个．13.如图，直线a∥b，直线c与直线a，b都相交，∠1=65°，则∠2= ______ °．【答案】65【解析】解：∵直线a∥b，∴∠1=∠2，∵∠1=65°，∴∠2=65°，故答案为：65．根据平行线的性质得出∠1=∠2，代入求出即可．本题考查了平行线的性质的应用，注意：两直线平行，同位角相等．14.如图，R t△ABC中，∠ACB=90°，D为斜边AB的中点，AB=10cm，则CD的长为______ cm．【答案】5【解析】解：∵∠ACB=90°，D为斜边AB的中点，∴CD=AB=×10=5cm．故答案为：5．根据直角三角形斜边上的中线等于斜边的一半可得CD=AB．本题考查了直角三角形斜边上的中线等于斜边的一半的性质，熟记性质是解题的关键．15.如图，在△ABC中，∠C=40°，CA=CB，则△ABC的外角∠ABD= ______ °．【答案】110【解析】解：∵CA=CB，∴∠A=∠ABC，∵∠C=40°，∴∠A=70°∴∠ABD=∠A+∠C=110°．故答案为：110．先根据等腰三角形的性质和三角形的内角和定理求出∠A，再根据三角形的外角等于等于与它不相邻的两个内角的和，进行计算即可．此题考查了等腰三角形的性质，用到的知识点是等腰三角形的性质、三角形的外角等于等于与它不相邻的两个内角的和．16.已知：m、n为两个连续的整数，且m＜＜n，则m+n= ______ ．【答案】7【解析】解：∵9＜11＜16，∴3＜＜4，∴m=3，n=4，∴m+n=3+4=7．故答案为：7．先估算出的取值范围，得出m、n的值，进而可得出结论．本题考查的是估算无理数的大小，先根据题意算出的取值范围是解答此题的关键．17.如图，有一直径是米的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC，则：（1）AB的长为______ 米；（2）用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为______ 米．【答案】1；【解析】解：（1）∵∠BAC=90°，∴BC为⊙O的直径，即BC=，∴AB=BC=1；（2）设所得圆锥的底面圆的半径为r，根据题意得2πr=，解得r=．故答案为：1，．（1）根据圆周角定理由∠BAC=90°得BC为⊙O的直径，即BC=，根据等腰直角三角形的性质得AB=1；（2）由于圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，则2πr=，然后解方程即可．本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．也考查了圆周角定理．三、解答题(本大题共1小题，共9.0分)18.计算：（2-1）0+|-6|-8×4-1+．【答案】解：原式=1+6-8×+4=1+6-2+4=9．【解析】本题涉及零指数幂、绝对值、负指数幂、二次根式化简四个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握零指数幂、绝对值、负指数幂、二次根式化简等考点的运算．四、计算题(本大题共1小题，共9.0分)19.先化简，再求值：（a+2）2+a（a-4），其中a=．【答案】解：（a+2）2+a（a-4）=a2+4a+4+a2-4a=2a2+4，当a=时，原式=2×（）2+4=10．【解析】首先利用完全平方公式和整式的乘法计算，再进一步合并得出结果，最后代入求得数值即可．此题考查整式的化简求值，注意先化简，再代入求值．五、解答题(本大题共7小题，共71.0分)20.已知：如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．【答案】证明：∵四边形ABCD是矩形，∴DC∥AB，DC=AB，∴CF∥AE，∵DF=BE，∴CF=AE，∴四边形AFCE是平行四边形，∴AF=CE．【解析】根据矩形的性质得出DC∥AB，DC=AB，求出CF=AE，CF∥AE，根据平行四边形的判定得出四边形AFCE是平行四边形，即可得出答案．本题考查了平行四边形的性质和判定，矩形的性质的应用，注意：矩形的对边相等且平行，平行四边形的对边相等．21.在一个不透明的箱子里，装有红、白、黑各一个球，它们除了颜色之外没有其他区别．（1）随机地从箱子里取出1个球，则取出红球的概率是多少？（2）随机地从箱子里取出1个球，放回搅匀再取第二个球，请你用画树状图或列表的方法表示所有等可能的结果，并求两次取出相同颜色球的概率．【答案】解：（1）∵在一个不透明的箱子里，装有红、白、黑各一个球，它们除了颜色之外没有其他区别，∴随机地从箱子里取出1个球，则取出红球的概率是：；（2）画树状图得：∵共有9种等可能的结果，两次取出相同颜色球的有3种情况，∴两次取出相同颜色球的概率为：=．【解析】（1）由在一个不透明的箱子里，装有红、白、黑各一个球，它们除了颜色之外没有其他区别，直接利用概率公式求解即可求得答案；（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次取出相同颜色球的情况，再利用概率公式即可求得答案．本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．22.如图，已知二次函数y=a（x-h）2+的图象经过原点O（0，0），A（2，0）．（1）写出该函数图象的对称轴；（2）若将线段OA绕点O逆时针旋转60°到OA′，试判断点A′是否为该函数图象的顶点？【答案】解：（1）∵二次函数y=a（x-h）2+的图象经过原点O（0，0），A（2，0）．解得：h=1，a=-，∴抛物线的对称轴为直线x=1；（2）点A′是该函数图象的顶点．理由如下：如图，作A′B⊥x轴于点B，∵线段OA绕点O逆时针旋转60°到OA′，∴OA′=OA=2，∠A′OA=60°，在R t△A′OB中，∠OA′B=30°，∴OB=OA′=1，∴A′B=OB=，∴A′点的坐标为（1，），∴点A′为抛物线y=-（x-1）2+的顶点．【解析】（1）由于抛物线过点O（0，0），A（2，0），根据抛物线的对称性得到抛物线的对称轴为直线x=1；（2）作A′B⊥x轴于B，先根据旋转的性质得OA′=OA=2，∠A′OA=60°，再根据含30度的直角三角形三边的关系得OB=OA′=1，A′B=OB=，则A′点的坐标为（1，），根据抛物线的顶点式可判断点A′为抛物线y=-（x-1）2+的顶点．本题考查了二次函数的性质：二次函数y=ax2+bx+c（a≠0）的顶点坐标为（-，），对称轴直线x=-，二次函数y=ax2+bx+c（a≠0）的图象具有如下性质：①当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，x＜-时，y随x的增大而减小；x＞-时，y 随x的增大而增大；x=-时，y取得最小值，即顶点是抛物线的最低点．②当a ＜0时，抛物线y=ax2+bx+c（a≠0）的开口向下，x＜-时，y随x的增大而增大；x ＞-时，y随x的增大而减小；x=-时，y取得最大值，即顶点是抛物线的最高点．也考查了旋转的性质．23.课外阅读是提高学生素养的重要途径．某校为了了解学生课外阅读情况，随机抽查了50名学生，统计他们平均每天课外阅读时间（t小时）．根据t的长短分为A，B，C，D四类，下面是根据所抽查的人数绘制的两幅不完整的统计图表．请根据图中提供的信息，解答下面的问题：50名学生平均每天课外阅读时间统计表（1）求表格中的的值，并在图中补全条形统计图；（2）该校现有1300名学生，请你估计该校共有多少名学生课外阅读时间不少于1小时？【答案】解：（1）50-10-20-15=5（名），故a的值为5，条形统计图如下：（2）1300×=520（名），答：估计该校共有520名学生课外阅读时间不少于1小时．【解析】（1）用抽查的学生的总人数减去A，B，C三类的人数即为D类的人数也就是a的值，并补全统计图；（2）先求出课外阅读时间不少于1小时的学生占的比例，再乘以1300即可．本题主要考查样本的条形图的知识和分析问题以及解决问题的能力．24.某学校开展“青少年科技创新比赛”活动，“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型．甲、乙两车同时分别从A，B两处出发，沿轨道到达C处，B在AC上，甲的速度是乙的速度的1.5倍，设t（分）后甲、乙两遥控车与B处的距离分别为d1，d2，则d1，d2与t的函数关系如图，试根据图象解决下列问题：（1）填空：乙的速度v2= ______ 米/分；（2）写出d1与t的函数关系式：（3）若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰，试探求什么时间两遥控车的信号不会产生相互干扰？【答案】40【解析】解：（1）乙的速度v2=120÷3=40（米/分），故答案为：40；（2）v1=1.5v2=1.5×40=60（米/分），60÷60=1（分钟），a=1，d1=；（3）d2=40t，当0≤t＜1时，d2+d1＞10，即-60t+60+40t＞10，解得0≤t＜2.5，∵0≤t＜1，∴当0≤t＜1时，两遥控车的信号不会产生相互干扰；当1≤t≤3时，d2-d1＞10，即40t-（60t-60）＞10，当1≤＜时，两遥控车的信号不会产生相互干扰综上所述：当0≤t＜2.5时，两遥控车的信号不会产生相互干扰．（1）根据路程与时间的关系，可得答案；（2）根据甲的速度是乙的速度的1.5倍，可得甲的速度，根据路程与时间的关系，可得a的值，根据待定系数法，可得答案；（3）根据两车的距离，可得不等式，根据解不等式，可得答案．本题考查了一次函数的应用，（1）利用了路程速度时间三者的关系，（2）分段函数分别利用待定系数法求解，（3）当0≤t＜1时，d2+d1＞10；当1≤t≤3时，d2-d1＞10，分类讨论是解题关键．25.如图，在锐角三角形纸片ABC中，AC＞BC，点D，E，F分别在边AB，BC，CA上．（1）已知：DE∥AC，DF∥BC．①判断四边形DECF一定是什么形状？②裁剪当AC=24cm，BC=20cm，∠ACB=45°时，请你探索：如何剪四边形DECF，能使它的面积最大，并证明你的结论；（2）折叠请你只用两次折叠，确定四边形的顶点D，E，C，F，使它恰好为菱形，并说明你的折法和理由．【答案】解：（1）如图1，①∵DE∥AC，DF∥BC，∴四边形DECF是平行四边形．②作AG⊥BC，交BC于G，交DF于H，∵∠ACB=45°，AC=24cm∴AG==12cm，设DF=EC=x，平行四边形的高为h，则AH=12h，∵DF∥BC，∴△ADF∽△ABC，∴=，∵BC=20cm，即：=∴x=×20，∵S=xh=×20h=20h-h2．∴h=-=-=6，∵AG=12cm，∴AF=FC，∴在AC中点处剪四边形DECF，能使它的面积最大．（2）①BC边向AC边折叠，使BC与AC重合，得到折痕交AB于D（CD为∠ACB的角平分线）；②C点向AB边折叠，使C点与D点重合，得到折痕交BC边于E，交AC边于F；通过上述两次折叠，得到点：DECF，组成的四边形为菱形．理由：∵CD和EF是四边形DECF对角线，而CD和EF互相垂直且平分，∴四边形DECF是菱形．（3）先折∠ACB的平分线（使CB落在CA上），折线与AB的交点为点D，再折DC的垂直平分线（使点C与点D重合），压平，折线与BC、CA的交点分别为E、F，展平后四边形DECF就是菱形．理由如下：由CB落在CA上，折现与AB的交点为点D，可得：∠ACD=∠BCD．由点C与点D重合，折线与BC、CA的交点分别为点E、F，可得：CF=DF=DE=CE，即四边形DECF为菱形．【解析】（1）①根据有两组对边互相平行的四边形是平行四边形即可求得，②根据△ADF∽△ABC推出对应边的相似比，然后进行转换，即可得出高h与x之间的函数关系式，根据平行四边形的面积公式，很容易得出面积S关于h的二次函数表达式，求出顶点坐标，就可得出面积s最大时h的值．（2）第一步BC边向AC边折叠，使BC与AC重合，得到折痕交AB于D（CD为∠ACB 对角线）；第二步C点向AB边折叠，使C点与D点重合，得到折痕交BC边于E，交AC 边于F ；通过上述两次折叠，得到点：DECF ，组成的四边形为菱形．本题考查了相似三角形的判定及性质、菱形的判定、二次函数的最值．关键在于根据相似三角形及已知条件求出相关线段的表达式，求出二次函数表达式，即可求出结论．26.如图，直线y =-x +3与x ，y 轴分别交于点A ，B ，与反比例函数的图象交于点P （2，1）．（1）求该反比例函数的关系式；（2）设PC ⊥y 轴于点C ，点A 关于y 轴的对称点为A ′；①求△A ′BC 的周长和sin ∠BA ′C 的值；②对大于1的常数m ，求x 轴上的点M 的坐标，使得sin ∠BMC= ．【答案】解：（1）设反比例函数的关系式y = ．∵点P （2，1）在反比例函数y = 的图象上，∴k =2×1=2．即反比例函数的关系式y =．（2）①过点C 作CD ⊥AB ，垂足为D ，如图1所示．当x =0时，y =0+3=3，则点B 的坐标为（0，3）．OB=3．当y =0时，0=-x +3，解得x =3，则点A 的坐标为（3，0），OA=3．∵点A 关于y 轴的对称点为A ′，∴OA ′=OA=3．∵PC ⊥y 轴，点P （2，1），∴OC=1，PC=2．∴BC=2．∵∠AOB=90°，OA ′=OB=3，OC=1，∴A ′B=3 ，A ′C= ．∴△A ′BC 的周长为3 + +2．∵S △A ′BC = BC •A ′O= A ′B •CD ，∴BC •A ′O=A ′B •CD ．∴2×3=3 ×CD ．∴CD= ．∵CD ⊥A ′B ，∴sin ∠BA ′C= ′==．∴△A′BC的周长为3++2，sin∠BA′C的值为．②方法一：由（2）知，d=，设M（t，0），∴BC=2，OM=t，BM=，CM=，∴d=，∴sin∠BCM=，∴2tm=×，∴t4+（10-4m2）t2+9=0，t2=2m2-5±2，①t2=2m2-5+2，t2=（m2-1）+2+（m2-4），∴t2=（+）2∴t1=+，t2=--，②t2=2m2-5-2，t2=（m2-1）-2+（m2-4），∴t2=（-）2∴t1=-，t2=-+，综上所述：当1＜m＜2时，满足要求的点M不存在；当m≥2时，满足要求的点M的坐标为（-，0）、（+，0）、（-+，0）、（--，0）．答题人：万老师方法二：当1＜m＜2时，作经过点B、C且半径为m的⊙E，连接CE并延长，交⊙E于点P，连接BP，过点E作EG⊥OB，垂足为G，过点E作EH⊥x轴，垂足为H，如图2①所示．∵CP是⊙E的直径，∴∠PBC=90°．∴sin∠BPC===．∵sin∠BMC=，∴∠BMC=∠BPC．∴点M在⊙E上．∵点M在x轴上∴点M是⊙E与x轴的交点．∵EG⊥BC，∴BG=GC=1．∴OG=2．∵∠EHO=∠GOH=∠OGE=90°，∴四边形OGEH是矩形．∴EH=OG=2，EG=OH．∵1＜m＜2，∴EH＞EC．∴⊙E与x轴相离．∴x轴上不存在点M，使得sin∠BMC=．②当m=2时，EH=EC．∴⊙E与x轴相切．Ⅰ．切点在x轴的正半轴上时，如图2②所示．∴点M与点H重合．∵EG⊥OG，GC=1，EC=m，∴EG==．∴OM=OH=EG=．∴点M的坐标为（，0）．Ⅱ．切点在x轴的负半轴上时，同理可得：点M的坐标为（-，0）．③当m＞2时，EH＜EC．∴⊙E与x轴相交．Ⅰ．交点在x轴的正半轴上时，设交点为M、M′，连接EM，如图2③所示．∵∠EHM=90°，EM=m，EH=2，∴MH===．∵EH⊥MM′，∴MH=M′H．∴M′H═．∵∠EGC=90°，GC=1，EC=m，∴EG===．∴OH=EG=．∴OM=OH-MH=-，∴OM′=OH+HM′=+，∴M（-，0）、M′（+，0）．Ⅱ．交点在x轴的负半轴上时，同理可得：M（-+，0）、M′（--，0）．综上所述：当1＜m＜2时，满足要求的点M不存在；当m≥2时，满足要求的点M的坐标为（-，0）、（+，0）、（-+，0）、（--，0）．【解析】（1）设反比例函数的关系式y=，然后把点P的坐标（2，1）代入即可．（2）①先求出直线y=-x+3与x、y轴交点坐标，然后运用勾股定理即可求出△A′BC的周长；过点C作CD⊥AB，垂足为D，运用面积法可以求出CD长，从而求出sin∠BA′C 的值．②由于BC=2，sin∠BMC=，因此点M在以BC为弦，半径为m的⊙E上，因而点M应是⊙E与x轴的交点．然后对⊙E与x轴的位置关系进行讨论，只需运用矩形的判定与性质、勾股定理等知识就可求出满足要求的点M的坐标．本题考查了用待定系数法求反比例函数的关系式、勾股定理、三角函数的定义、矩形的判定与性质、直线与圆的位置关系、垂径定理等知识，考查了用面积法求三角形的高，考查了通过构造辅助圆解决问题，综合性比较强，难度系数比较大．由BC=2，sin∠BMC=联想到点M在以BC为弦，半径为m的⊙E上是解决本题的关键．。

2013-2014学年福建省泉州一中八年级（下）期末数学试卷一．选择题（每题3分，共21分）1．（3分）要使分式有意义，则x应满足的条件是（）A．x≠2 B．x≠﹣2 C．x≠0 D．x＞22．（3分）若y=kx﹣4的函数值y随着x的增大而减小，则k的值可能是下列的（）A．πB．C．0 D．﹣43．（3分）在5月份的地理学科市质检后，叶老师调查了班上某小组10名同学的地理成绩如下：85，83，81，81，87，73，82，79，81，7 9，则这组数据的中位数，众数分别为（）A．80，81 B．81，81 C．81，89 D．73，814．（3分）矩形具有而菱形不具有的性质是（）A．对角线互相平分 B．对角线互相垂直C．对角线相等D．对角线平分一组对角5．（3分）如图，丝带重叠的部分一定是（）A．正方形B．矩形C．菱形D．都有可能6．（3分）如图，点P在反比例函数y=的图象上，过P点作PA⊥x轴于点A，作PB⊥y轴于B点，矩形OAPB的面积为（）A．1 B．2 C．4 D．8定的污水处理池，池的底面积S（m2）与其深度h（m）满足关系式：V=Sh（V ≠0），则S关于h的函数图象大致是（）A．B．C．D．二．填空题（每小题4分，共40分）的坐标=分）计算：0.009.3环，15．（4分）函数y=kx+b的图象如图，则不等式kx+b≥0的解集是．16．（4分）如图，菱形ABCD的周长为8，对角线AC和BD相交于点O，AC：BD=1：2，则AO：BO=，菱形ABCD的面积S=．17．（4分）有一数值转换器，原理如图所示，若开始输入x的值是7，可发现第1次输出的结果是12，第2次输出的结果是6，第3次输出的结果是，依次继续下去…，第2014次输出的结果是．三．解答题（共89分）18．（9分）计算：（4﹣π）0+|﹣2|﹣16×4﹣1+16÷23．19．（9分）先化简，再求值：，其中．20．（9分）某服装制造厂要在开学前赶制3000套校服，为了尽快完成任务，厂领导合理调配，加强第一线人力，使每天完成的校服比原计划多20%，结果提前4天完成任务，问原计划每天能完成多少套校服？21．（9分）如图：正方形ABCD的一条对角线AC的长为4cm，求它的边长和面积．（长度精确到0.1cm）22．（9分）某校八年级（1）班举行了“我的中国梦”的专题测试，全班同学的成绩按A、B、C、D四个等级进行统计，并将统计结果绘制成如下两幅统计图，请你结合图中所给信息解答下列问题：（说明：A级90～100分；B级75﹣；C级60～74分；D级60分以下）（1）求出该校八年级（1）班总学生数；（2）求出扇形统计图中C级所在的扇形圆心角度数；直接说出该班学生“我的中国梦”的专题测试成绩的中位数落在哪个等级内．23．（9分）如图，一次函数y=kx+b的图象与反比例函数y=的图象交于A、B 两点．（1）利用图中条件求反比例函数和一次函数的解析式；（2）根据图象直接写出使一次函数的值大于反比例函数的值的x取值范围．24．（9分）如图，在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，CE∥BF，连接BE、CF．（1）求证：△BDF≌△CDE；（2）若AB=AC，求证：四边形BFCE是菱形．25．（13分）某火车站有甲种货物60吨，乙种货物90吨，现计划用30节A、B 两种型号的车厢将这批货物运出．设30节车厢中有A型车厢a节，（1）请用含a的代数式表示30节车厢中有B型车厢的节数；（2）如果甲种货物全部用A型车厢运送，乙种货物全部用B型车厢运送，则A 型、B型车厢平均每节运送的货物吨数刚好相同，请求出a的值；（3）在（2）的条件下，已知每节A型车厢的运费是x万元，每节B型车厢的运费比每节A型车厢的运费少1万元，设总运费为y万元，求y与x之间的函数关系式．如果已知每节A型车厢的运费不超过5万元，而每节B型车厢的运费又不低于1.5万元，求总运费y的最小值．26．（13分）已知，矩形OABC在平面直角坐标系内的位置如图所示，点O为坐标原点，点A的坐标为（10，0），点B的坐标为（10，8）．（1）直接写出点C的坐标为：C（，）；（2）已知直线AC与双曲线在第一象限内有一交点Q为（5，n）；①求m及n的值；②若动点P从A点出发，沿折线AO→OC的路径以每秒2个单位长度的速度运动，到达C处停止．求△OPQ的面积S与点P的运动时间t（秒）的函数关系式，并求当t取何值时S=10．2013-2014学年福建省泉州一中八年级（下）期末数学试卷参考答案与试题解析一．选择题（每题3分，共21分）1．（3分）要使分式有意义，则x应满足的条件是（）A．x≠2 B．x≠﹣2 C．x≠0 D．x＞2【解答】解：根据题意得：x﹣2≠0，解得：x≠2．故选：A．2．（3分）若y=kx﹣4的函数值y随着x的增大而减小，则k的值可能是下列的（）A．πB．C．0 D．﹣4【解答】解：∵y随着x的增大而减小，∴k＜0，故选：D．3．（3分）在5月份的地理学科市质检后，叶老师调查了班上某小组10名同学的地理成绩如下：85，83，81，81，87，73，82，79，81，7 9，则这组数据的中位数，众数分别为（）A．80，81 B．81，81 C．81，89 D．73，81【解答】解：这组数据按照从小到大的顺序排列为：73，79，79，81，81，81，82，83，85，87，则中位数为：81，众数为81．故选：B．4．（3分）矩形具有而菱形不具有的性质是（）A．对角线互相平分 B．对角线互相垂直C．对角线相等D．对角线平分一组对角【解答】解：A、对角线互相平分是菱形矩形都具有的性质，故A选项错误；B、对角线互相垂直是菱形具有而矩形不具有的性质，故B选项错误；C、矩形的对角线相等，菱形的对角线不相等，故C选项正确；D、对角线平分一组对角是菱形具有而矩形不具有的性质，故D选项错误；故选：C．5．（3分）如图，丝带重叠的部分一定是（）A．正方形B．矩形C．菱形D．都有可能【解答】解：过点A作AE⊥BC于E，AF⊥CD于F，因为两条彩带宽度相同，所以AB∥CD，AD∥BC，AE=AF．∴四边形ABCD是平行四边形．∵S▱ABCD=BC•AE=CD•AF．又AE=AF．∴BC=CD，∴四边形ABCD是菱形．故选：C．6．（3分）如图，点P在反比例函数y=的图象上，过P点作PA⊥x轴于点A，作PB⊥y轴于B点，矩形OAPB的面积为（）A．1 B．2 C．4 D．8【解答】解：∵PA⊥x轴于点A，PB⊥y轴于B点，∴矩形OAPB的面积=|2|=2．故选：B．7．（3分）为了更好保护水资源，造福人类，某工厂计划建一个容积V（m3）一定的污水处理池，池的底面积S（m2）与其深度h（m）满足关系式：V=Sh（V ≠0），则S关于h的函数图象大致是（）A．B．C．D．【解答】解：∵V=Sh（V为不等于0的常数），∴S=（h≠0），S是h的反比例函数．依据反比例函数的图象和性质可知，图象为反比例函数在第一象限内的部分．故选：C．二．填空题（每小题4分，共40分）8．（4分）在平面直角坐标系中，点P（﹣2，1）关于原点的对称点P′的坐标是（2，﹣1）．【解答】解：点P（﹣2，1）关于原点的对称点P′的坐标是（2，﹣1）．故答案为：（2，﹣1）．9．（4分）计算：+=1．【解答】解：原式===1．故答案为：1．10．（4分）计算：=．【解答】解：=，故答案为：．11．（4分）在平行四边形ABCD中，∠A﹦80°，则∠B=100°．【解答】解：∵四边形ABCD是平行四边形，∴BC∥AD，∴∠A+∠B=180°，∴∠B=180°﹣∠A=180°﹣80°=100°．故答案为100°．12．（4分）自2013年2月以来，H7N9禽流感在我国流行．该病毒的直径是0.00 000 012米，用科学记数法表示为 1.2×10﹣7米．【解答】解：0.00 000 012=1.2×10﹣7；故答案为：1.2×10﹣7．13．（4分）甲、乙、丙、丁四位选手各射击10次，每人的平均成绩都是9.3环，方差如下表：则这四人中成绩发挥最稳定的是乙选手．【解答】解：∵S甲2=0.035，S乙2=0.016，S丙2=0.022，S丁2=0.025，∴S乙2＜S丙2＜S丁2＜S甲2，∴这四人中成绩发挥最稳定的是乙；故答案为：乙．14．（4分）小王某学期的物理成绩分别为：平时平均成绩得84分，期中考试得90分，期末考试得85 分．若按如图所显示的权重，那么小王该学期的总评成绩应该为86.4分．【解答】解：根据题意得：84×10%+90×30%+85×60%=86.4（分），答：小王该学期的总评成绩应该为86.4分．故答案为：86.4．15．（4分）函数y=kx+b的图象如图，则不等式kx+b≥0的解集是x≤﹣2．【解答】解：根据题意得当x≤﹣2时，y≥0，所以不等式kx+b≥0的解集是x≤﹣2．故答案为x≤﹣2．16．（4分）如图，菱形ABCD的周长为8，对角线AC和BD相交于点O，AC：BD=1：2，则AO：BO=1：2，菱形ABCD的面积S=16．【解答】解：∵四边形ABCD是菱形，∴AO=CO，BO=DO，∴AC=2AO，BD=2BO，∴AO：BO=1：2；∵菱形ABCD的周长为8，∴AB=2，∵AO：BO=1：2，∴AO=2，BO=4，∴菱形ABCD的面积S==16，故答案为：1：2，16．17．（4分）有一数值转换器，原理如图所示，若开始输入x的值是7，可发现第1次输出的结果是12，第2次输出的结果是6，第3次输出的结果是3，依次继续下去…，第2014次输出的结果是8．【解答】解：第2次输出的结果是6，第3次输出：×6=3，第4次输出：3+5=8，第5次输出：×8=4，第6次输出：×4=2，第7次输出：×2=1，第8次输出：1+5=6，第9次输出：×6=3，…，∵（2014﹣1）÷6=335余3，∴第2014次输出的结果与第4次输出的结果相同，是8．故答案为：3，8．三．解答题（共89分）18．（9分）计算：（4﹣π）0+|﹣2|﹣16×4﹣1+16÷23．【解答】解：原式=1+2﹣4+2=1．19．（9分）先化简，再求值：，其中．【解答】解：原式=（+）•=•+•=+=2x当x=时，原式=2．20．（9分）某服装制造厂要在开学前赶制3000套校服，为了尽快完成任务，厂领导合理调配，加强第一线人力，使每天完成的校服比原计划多20%，结果提前4天完成任务，问原计划每天能完成多少套校服？【解答】解：设原计划每天生产x套校服，则实际每天生产（1+20%）x套校服，由题意得，﹣=4，解得：x=125，经检验：x=125是原分式方程的解，且符合题意．答：原计划每天生产125套校服．21．（9分）如图：正方形ABCD的一条对角线AC的长为4cm，求它的边长和面积．（长度精确到0.1cm）【解答】解：∵四边形ABCD为正方形，∴AB=BC，∠ABC=90°，故AC=AB，即AB=2≈2.8cm，故正方形的面积S=a2=8cm2，答：正方形的边长为2.8cm，面积为8cm2．22．（9分）某校八年级（1）班举行了“我的中国梦”的专题测试，全班同学的成绩按A、B、C、D四个等级进行统计，并将统计结果绘制成如下两幅统计图，请你结合图中所给信息解答下列问题：（说明：A级90～100分；B级75﹣；C级60～74分；D级60分以下）（1）求出该校八年级（1）班总学生数；（2）求出扇形统计图中C级所在的扇形圆心角度数；直接说出该班学生“我的中国梦”的专题测试成绩的中位数落在哪个等级内．【解答】解：（1）13+25+10+2=50（人），答：该校八年级（1）班总学生数共50人；（2）C级所在的扇形圆心角度数：360°×=72°；根据中位数定义可得：该班学生“我的中国梦”的专题测试成绩的中位数落在B等级内．23．（9分）如图，一次函数y=kx+b的图象与反比例函数y=的图象交于A、B 两点．（1）利用图中条件求反比例函数和一次函数的解析式；（2）根据图象直接写出使一次函数的值大于反比例函数的值的x取值范围．【解答】解：（1）从图象可知A的坐标是（﹣2，﹣1），B的坐标是（1，n），把A的坐标代入反比例函数的解析式得：k=2，即反比例函数的解析式是y=，把B的坐标代入反比例函数的解析式得：n=2，即B的坐标是（1，2），把A、B的坐标代入一次函数的解析式得：解得：k=1，b=1，即一次函数的解析式是y=x+1；（2）使一次函数的值大于反比例函数的值的x取值范围是x＞1或﹣2＜x＜0．24．（9分）如图，在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，CE∥BF，连接BE、CF．（1）求证：△BDF≌△CDE；（2）若AB=AC，求证：四边形BFCE是菱形．【解答】证明：（1）∵CE∥BF，∴∠ECD=∠FBD，∠DEC=∠DFB；又∵D是BC的中点，即BD=DC，∴△BDF≌△EDC；（AAS）（2）∵AB=AC，∴△ABC是等腰三角形；又∵BD=DC，∴AD⊥BC（三线合一），由（1）知：△BDF≌△EDC，则DE=DF，DB=DC；∴四边形BFCE是菱形（对角线互相平分且互相垂直的四边形为菱形）．25．（13分）某火车站有甲种货物60吨，乙种货物90吨，现计划用30节A、B 两种型号的车厢将这批货物运出．设30节车厢中有A型车厢a节，（1）请用含a的代数式表示30节车厢中有B型车厢的节数；（2）如果甲种货物全部用A型车厢运送，乙种货物全部用B型车厢运送，则A 型、B型车厢平均每节运送的货物吨数刚好相同，请求出a的值；（3）在（2）的条件下，已知每节A型车厢的运费是x万元，每节B型车厢的运费比每节A型车厢的运费少1万元，设总运费为y万元，求y与x之间的函数关系式．如果已知每节A型车厢的运费不超过5万元，而每节B型车厢的运费又不低于1.5万元，求总运费y的最小值．【解答】解：（1）∵现计划用30节A、B两种型号的车厢将这批货物运出，设30节车厢中有A型车厢a节，∴30节车厢中有B型车厢的节数为：（30﹣a）节；（2）根据题意可得：=，解得：a=12，经检验得：a=12是原方程的解，答：a的值为12；（3）当a=12时，30﹣a=18，y=12x+18（x﹣1）=30x﹣18，又∵，∴2.5≤x≤5，∵y=30x﹣18是关于x的一次函数，k=30＞0，∴y随x的增大而增大，又∵2.5≤x≤5，∴当x=2.5时，y的最小值是：y=30×2.5﹣18=57，答：运费的最小值为57万元．26．（13分）已知，矩形OABC在平面直角坐标系内的位置如图所示，点O为坐标原点，点A的坐标为（10，0），点B的坐标为（10，8）．（1）直接写出点C的坐标为：C（0，8）；（2）已知直线AC与双曲线在第一象限内有一交点Q为（5，n）；①求m及n的值；②若动点P从A点出发，沿折线AO→OC的路径以每秒2个单位长度的速度运动，到达C处停止．求△OPQ的面积S与点P的运动时间t（秒）的函数关系式，并求当t取何值时S=10．【解答】解：（1）C（0，8）…（3分）（2）①设直线AC的解析式为y=kx+b（k≠0），过A（10，0）、C（0，8），解得：∴直线AC的解析式为…（5分）又∵Q（5，n）在直线AC上，∴，…（6分）又∵双曲线过Q（5，4），∴m=5×4=20…（7分）②当0≤t≤5时，OP=10﹣2t，…（8分）过Q作QD⊥OA，垂足为D，如图1∵Q（5，4），∴QD=4，∴，…（9分）当S=10时，20﹣4t=10解得t=2.5…（10分）当5＜t≤9时，OP=2t﹣10，…（11分）过Q作QE⊥OC，垂足为E，如图2∵Q（5，4），∴QE=5，∴，…（12分）当S=10时，5t﹣25=10解得t=7综上，S=，当t=5秒时，△OPQ的面积不存在，∴当t=2.5秒或t=7秒时，S=10．…（13分）。

惠安县2014年初中学业质量测查（第二轮）数 学 试 题（满分：150分；考试时间120分钟）温馨提示：所有答案必须填写到答题卡相应的位置上，答在本试卷上一律无效.一、选择题（每题3分，共21分）每小题有四个答案，其中有且只有一个答案是正确的，请在答题卡上相应题目的答题区域内作答，答对的得3分，答错、不答或答案超过一个的一律得0分. 1．14的相反数是（ ）． A ．4 B ．-4 C ．14-D ．142．实数a 、b 在数轴上的位置如图所示，下列式子错误．．的是（ ）．A . -a ＜ -bB . |a | ＞ |b |C . a ＜ bD . b -a ＞ 0 3．下列计算正确的是（ ）. A ．32a a a -=B ．236a a a ⋅= C ．326()a a = D ．33(3)9a a =4．如图所示的物体的左视图是（ ）．5．依次连接等腰梯形各边中点，得到的四边形一定是（ ）．A ．矩形B ．菱形C ．正方形D ．梯形6．在某校“我的中国梦”演讲比赛中，有7名学生参加决赛，他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前4名，不仅要了解自己的成绩，还要了解这7名学生成绩的（ ）．A ．众数B ．方差C ．平均数D ．中位数 7．如图，在△ABC 中，AB = AC = 2，∠BAC = 20°．动点P 、Q 分别在直线BC 上运动，且始终保持∠P AQ = 100°．设BP = x ，CQ = y ，则y 与x 之间的函数关系用图象大致可以表示为二、填空题（每题4分，共40分）在答题卡上相应题目的答题区域内作答. 8．4的平方根为 ．9．分解因式：x 2 -4x + 4 = ． 10．拒绝“餐桌浪费”，刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克，这B ． A ． ．C ．D ． 正面（第7题图）A. B. C. D.个数据用科学记数法表示为 ． 11．七边形的内角和等于 度． 12．计算：4511x x x +---= ． 13．直线y = -2x -1不经过．．．第 象限． 14．如图△ABC 中，∠A = 90°，点D 在AC 边上，DE ∥BC ，若∠1 = 155°，则∠C 的度数为 °．15．如图，菱形ABCD 的边长是2cm ，∠A = 60°，点E 、F 分别是边AB 、CD 上的动点，则线段EF 的最小值为_______ cm ．16．底面半径为1，母线长为4的圆锥的侧面积等于 ．17．如图所示，直角坐标平面xoy 内，动点P 按图中箭头所示方向依次运动，第1次从点(-1,0)运动到点(0, 1)，第2次运动到点(1, 0)，第3次运动到点(2, -2)，……，按这样的运动规律，动点P 第11次运动到点（ ， ）；第2014次运动到点（ ， ）．三、解答题（共89分）在答题卡上相应题目的答题区域内作答. 18．（9201421|5|(1)()2----+． 19．（9分）先化简，再求值：(3x + 2)(3x ﹣2)﹣9x (x ﹣1)，其中x=120．（9分）从甲学校到乙学校有A 、B 、C 三条线路，从乙学校到丙学校有E 、F 二条线路．请用树状图或列表的方法，求小明随机选择一条从甲学校出发经过乙学校到达丙学校的行走路线，并求恰好经过了E 线路的概率.21．（9分）如图，E 、F 是平行四边形ABCD 的对角线AC 上的点，且CE = AF ．求证：BE = DF ．22．（9分）某企业500名员工参加安全生产知识测试，成绩记为A 、B 、C 、D 、E 共5个等级，为了解本次测试的成绩（等级）情况，现从中随机抽取部分员工的成绩（等级），统计整理并制作了如下两个不完全的统计图．请根据图中提供信息，解答下面问题．（1）这次抽样调查中，样本容量为 ；E 级所在扇形的圆心角度数为_______°，请补全图①；（2）如果测试成绩（等级）为A 、B 、C 级的定为优秀．．，请估计该企业参加本次安全生产（第14题图）C （第15题图）Dyx (7,0) (5,0) (6,-2)(3,0) (4,1) (0,1) (1,0)(2,-2)O (-1,0) （第17题图）人数知识测试成绩（等级）达到优秀．．的员工的总人数．23．（9分）如图，已知直线l 分别与x 轴、y 轴交于A 、B 两点，与双曲线 (a ≠ 0，x＞0)分别交于D 、E 两点.若点D 的坐标为(4, 1)，点E 的坐标为(1, 4). （1）分别求出直线l 与双曲线的解析式；（2）若将直线l 向下平移m （m ＞0）个单位，当m 为何值时，直线l 与双曲线有且只有一个公共点？24．（9分）学校课外生物小组的试验园地是长32m 、宽20m 的矩形，为便于管理，现要在试验园地开辟水平宽度均为x m 的小道（图中阴影部分）. （1）如图1所示，在试验园地开辟一条水平宽度相等小道，则剩余部分面积为____________m 2（用含x 的代数式表示）；（2）如图2所示，在试验园地开辟水平宽度相等的三条小道，其中有两条道路相互平行.25．（13分）如图，已知抛物线2y x bx c =++经过点（1, -5）和（-2, 4）.（1）求这条抛物线的解析式；（2）设此抛物线与直线y x =相交于点A ，B （点B 在点A 的右侧），平行于y 轴的直线x= m (01)m <<与抛物线交于点M ，与直线y x =交于点N ，交x 轴于点P ，求线段MN 的长（用含m 的代数式表示）；（3）在条件（2）的情况下，连接OM 、BM ，是否存在m 的值，使△BOM 的面积S 最大？若存在，请求出m 的值；若不存在，请说明理由．（图①） （图1）（图2）= x（图②） a y x=20 15 105 205 5 826．（13分）如图，等腰梯形ABCD中，AD∥BC，下底边AD在x轴上，AB=BC=CD=2且点A(-1,0).动点M、N均以每秒1个单位的相同速度从点A、D同时出发，分别沿A→B→C 和D→A运动，当点N到达点A时，M、N同时停止运动.设运动时间为t秒.（1）请直接写出．．B、D两点的坐标；（2）若以MN为直径的圆与直线BC相切，试求出此时t的值；（3）当t=3秒时，在线段OD的垂直平分线上是否存在点P，使得∠DPO=∠DMO？若存在，请求出点P的纵坐标；若不存在，请说明理由.2014年惠安县初中学业质量检查数学试题参考答案及评分标准说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分．（二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分． （三）以下解答各行右端所注分数表示正确做完该步应得的累计分数．一、选择题（每小题3分，共21分）1. C 2. A 3. C 4. D 5. B 6. D 7. A. 二、填空题（每小题4分，共40分）8．±2 9．(x -2)2 10．5×1010 11．9000 12．113．一 14．250 1516．4π 17．(1)（10,-2）；(2)（2013,0）. 三、解答题（9个小题，共89分） 18．（9201421|5|(1)()2----+. 解：原式 = 4 - 5-1 +4 ………………………………………………………………8分 = 2 ………………………………………………………………………9分19．（9分）先化简，再求值：(3x + 2)(3x ﹣2)﹣9x (x ﹣1)，其中x=1解：原式 = 9x 2 – 4 – 9x 2 + 9x ………………………………………………………4分= 9x – 4 ………………………………………………………………6分 当x= 1 原式= 9(1 – 4 …………………………………………7分= 5 –………………………………………………9分20．（9分）解：甲 乙 丙 …………………………………5分小明从甲校出发经过乙校到达丙学校共有6种行走路线，…………………………………6分 其中恰好经过E 线路的情况有3种…………………………………7分∴P （过E 线路）=3162=. ………………………………………………………………9分 法2：列表略21．（9分）证明：在□ABCD 中，AD ∥BC 且AD = BC∴∠1 =∠2……………………………………………3分在△ADF 和△CBE 中，⎧=⎪∠=∠⎨⎪=⎩12AD BCAF CE ，……………6分∴△ADF ≌ △CBE ， ………………………8分ABCE F∴AE = BD . ……………………………………9分方法2：亦可通过证明△BAE ≌ △DCF .（参照以上评分标准给分）22．（9分）（1）50，360，图略，…………………………………………………………6分 （2）达到优秀等级的员工人数为：500×508550--= 370（人）. ……………9分 23．（9分）解：（1）设直线解析式y = kx + b （k ≠0）， 双曲线解析式k y x'=)0(≠'k ………………………………………………2分 依题意，得⎩⎨⎧=+=+4,14b k b k 与 41k '=……………………………………4分解得⎩⎨⎧=-=51b k 与 k′ = 4∴直线解析式为y =-x + 5， 双曲线解析式4y x= …………………………………………………………………6分（2）法1：如图，直线l 向下平移m 个单位后的直线解析式为y =-x + 5 -m ………………7分∵直线l 与双曲线只有一个公共点，又由双曲线的轴对称性质，可设公共点为(n , n ) 即n 2 = 4， ∴n 1 = 2，n 2 = -2（不合舍去）………………………………………8分 即交点为(2, -2)，代入平移后的直线解析式为：2 = -2 + 5 -m∴m = 1 ………………………………………………………………………………9分 法2：如图，直线l 向下平移m 个单位后的直线解析式为y =-x + 5 –m ………………7分⎪⎩⎪⎨⎧-+-==mx y x y 5,4 若直线l 与双曲线只有一个公共点，则△= b 2 -4ac = (m -5)2 –16 = 0 ∴m 1 = 1，m 2 = 9（不合舍去）∴m = 1时，直线l 与双曲线有且只有一个公共点. ……………………9分 24．（9分）（1）20（32 - x ）…………………………………………………………3分 （2）依题意，得（32 -2 x ）·（20 -x ）= 570 (7)分解得x 1 = 1，x 2 = 35（不合舍去） ………………………………………………………8分答：小道宽为1米. ………………………………………………………………………9分即x 2 + (m -5)x + 4 = 0……………………8分25．（13分）解：（1）∵点（1, -5）和（-2, 4）在抛物线2y x bx c =++上⎩⎨⎧=+--=++424,51c b c b 即 ⎩⎨⎧-=-=4,2c b …………………………………………………2分∴抛物线解析式为224y x x =-- ……………………………………………………3分 （2）如图可知，∵M P N x x x m ===∴N (m , m )，M (m , m 2- 2m - 4) ……………………………………………………４分由（1）知224y x x =--，令0y =，得11x =21x =即为抛物线与x 轴两个交点的横坐标，∴当01m <<，点N 在点M 的上方……………………………………………………５分 ∴MN = y N - y M= m -(m 2 - 2m -4)= - m 2 + 3m + 4………………………………………………………………………………7分 （3）存在；由（２）得MN = - m 2 + 3m + 4 联立方程组⎩⎨⎧--==42,2x x y x y 解得⎩⎨⎧==⎩⎨⎧-=-=441,12211y x y x ∴A (-1, -1)，B (4, 4) ………………………………9分 作BC ⊥MN 于点C ，则BC =4—m ，OP =m ，S =12MN ·OP +12MN ·BC =2（—m 2+3m +4） 23252()22m =--+………………………………12分∵—2＜0， ∴当m =32时，S 有最大值………………………………13分26. （9分）解：（1）B （、D （3,0） …………………3分 （2）分两种情况， ①如图1， 当0≤t ≤2时∵Rt △AOB 中，∠AOB = 900，AO =12AB ∴∠BAO = 600，∴()22t M -，(3,0)N t - …………………4分则以MN 为直径的圆心O ′(1,)44t -过O ′作O ′G ⊥BC ，交BC 于点G则(14tG -……………………………………………………………5分法1：当以MN 为直径的圆与直线BC 相切，则O ′G =12MN4=即1243t t ==…………………………………………………………………………6分 法2：可用1MG NG k k ⋅=-或构造相似或勾股定理等方法求出t （可参照方法1给分）② 如图2，当2＜t ≤4时若以MN 为直径的圆与直线BC 相切，则MN ⊥BC ∴BM = ON 即t -2 =3 -t∴52t = ……………………………………8分 综上，当43t =或52t =时，以MN 为直径的圆与直线BC 相切（3）存在如图3，当t = 3时，(1M ………………………9分若∠DPO = ∠DMO则存在⊙Q ，使得点O 、D 、P 、M 在⊙Q 上， 又点Q 在OD 的垂直平分线上，可设Q 3(,)2n∴QM = QO =解得6n =，即3(,26Q ……………………………10分∴PQ OQ ===…………………………………11分① 当点P 在点Q 上方时3P Q y PQ y =+=+……………………………………12分 ② 当点P 在点Q 下方时由对称性质，可得63P y '=-综上所述：点P 的纵坐标为36+或63-13分。

（第20题图）2014年福建省泉州市初中学业质量检查数 学 试 卷（试卷满分:150分；考试时间:120分钟） 友情提示：所有答案必须填写到答题卡相应的位置上．一、选择题（每小题3分，共21分）每小题有四个答案，其中有且只有一个答案是正确的，请在答题卡上相应题目的答题区域内作答，答对的得3分，答错或不答的一律得0分． 1．计算：3×（-1）等于（ ）．A ．0B ．3C ．3D ． 3- 2．计算：23)(a 等于（ ）．A ．5aB ．6a C ．32a D ．a 63．如图，数轴上表示的是某不等式组的解集，则这个不等式组可以是（ ）．A ．12x x ≥-⎧⎨<⎩B ．12x x ≤-⎧⎨<⎩C ．12x x >-⎧⎨≤⎩D ．12x x ≥-⎧⎨>⎩4．在某次体育测试中，九年级某班7位同学的立定跳远成绩（单位：m ）分别为：2.15，2.25，2.25，2.31，2.42，2.50，2.51，则这组数据的中位数是（ ）． A ．2.15 B ．2.25 C ．2.31 D ．2.42 5．若n 边形的内角和是1080︒，则n 的值是（ ）． A ．6 B ．7 C ．8 D ．96．如图是一个正方体被截去一角后得到的几何体，它的俯视图是（ ）．7．如图，在ABC Rt ∆中,90BAC ∠=︒, D 、E 分别是AB 、BC 的中点, F 在 CA 的延长线上，FDA B ∠=∠，AC=6，AB=8，则四边形AEDF 的周 长为（ ）．A ．22 Ｂ．20 Ｃ．18 Ｄ．16二、填空题（每小题4分，共40分）在答题卡上相应题目的答题区域内作答． 8．-2的相反数是 ． 9．分解因式：23a a += ．10．世界文化遗产长城总长约为6 700 000 m ，将6 700 000用科学记数法表示为 ．11．计算：222a a a -=-- ． 12．方程311x =-的解是 ．13．在菱形ABCD 中，AB=3cm ，则菱形ABCD 的周长为 cm ． 14．已知扇形的圆心角为120︒，弧长是4πcm ，则扇形的半径是 cm ． 15．如图，点C 在直线MN 上，AC BC ⊥于点C ，165∠=°，则2∠= °． 16．如图，点A 在函数6y x=．（x >0）的图象上，过点A 作AH y ⊥轴，点P 是x 轴上的一个动点，连结P A 、PH ，则APH ∆的面积为 ．17．如图，在边长为1的小正方形网格中，点A 、B 、C 、D 都在这些小正方形的顶点上，连结AB ． （1）AB 的长为 ；（2）连结CD 与AB 相交于点P ，则APD ∠tan 的值是 ．三、解答题（共89分）在答题卡上相应题目的答题区域内作答． 18．（91082(1)3π-⨯--+-．19．（9分）先化简，再求值：2(2)(2)(2)x x x +-+-，其中12x =-．20．（9分）已知：如图，在ABC ∆中，AB=AC ，D 为BC 的中点，过点D 作DE ⊥AB ，DF ⊥AC ，垂足分别为E 、F ．求证：BED ∆≌CFD ∆．（第6题图）（第3题图）A（第7题图）BCDEFBACMN12（第15题图）（第16题图）（第17题图）ABCDP21．（9分）某校举办“科技创新”作品评比，作品上交时限为3月1日至30日，组委会把同学们交来的作品按时间顺序每5天组成一组，共分成六组，现对每一组的件数进行统计，绘制成如图所示的不完全统计图．已知第二组与第四组的件数比为1∶2．请你回答 （1）本次活动共有 件作品参赛，并把条形统计图补充完整．．．．．．．．．．．； （2）经评比，第四组和第六组分别有10件和2件作品获奖，那么你认为这两组哪个组获奖率较高？为什么？22．（9分）某市举办中学生足球赛，初中男子组共有市直学校的A 、B 两队和县区学校的e 、f 、g 、h 四队报名参赛，六支球队分成甲、乙两组，甲队由A 、e 、f 三队组成，乙组由B 、g 、h 三队组成，现要从甲、乙两组中各随机抽取一支球队进行首场比赛． （1）在甲组中，首场比赛抽e 队的概率是 ；（2）请你用画树状图或列表的方法，求首场比赛出场的两个队都是县区学校队的概率．23．（9分）如图，已知ABC ∆的三个顶点的坐标分别为A （-2,3）、B （-6,0）、C （-1,0）． （1）请画出ABC ∆绕坐标原点O 逆时针．．．旋转90°后的A B C '''∆,并直接写出点B 的对应点B '的坐标；（2）请直接写出D 的坐标，使得以A 、B 、C 、D 为顶点的四边形是平行四边形．24．（9分）某服装专卖店计划购进甲、乙两种新款服装共100件，其进价与售价如表所示：（1）若该专卖店计划用42000元进货，则这两种新款服装各购进多少件？（2）若乙的数量不能超过甲的数量的2倍，试问：应怎样进货才能使专卖店在销售完这批服装时获利最多？并求出最大利润．25．（13分）已知顶点为P 的抛物线1C 的解析式是2(3)(0)y a x a =-≠，且经过点（0，1）．（1）求a 的值；（2）如图，将抛物线1C 向下平移h （h >0）个单位得到抛物线2C ，过点K （0，2m ）（m >0）作直线l 平行于x点关于y 轴对称．①点G 在抛物线1C 上，当m 为何值时，四 边形APCG 是平行四边形？②若抛物线1C 的对称轴与直线l 交于点E ，与抛物线2C 交于点F ．试探究：在K 点 运动过程中，KCPF的值是否会改变？若会， 请说明理由；若不会，请求出这个值．26．（13分）在平面直角坐标系中，O 为坐标原点，已知点F （，0），直线GF 交y 轴正半轴于点G ，且．30GFO ∠=︒ （1）直接写出点G 的坐标；（2）若⊙O 的半径为1，点P 是直线GF 上的动点，直线P A 、PB 分别与⊙O 相切于点A 、B ．①求切线长PB 的最小值；②问：在直线GF 上是否存在点P ，使得 60APB ∠=︒?若存在，请求出P 点的坐标；若不存在，请说明理由．参赛作品件数条形统计图（第21题图）（第23题图）（第25题图）（第26题图）（第20题图）2014年福建省泉州市初中学业质量检查数学试题参考答案及评分标准说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分． （二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分．（三）以下解答各行右端所注分数表示正确做完该步应得的累计分数． 一、选择题（每小题3分，共21分）1．D 2．B 3．A 4．C 5．C 6．A 7．D 二、填空题（每小题4分，共40分）8．2 9．(3)a a + 10．66.710⨯ 11．1 12．4x = 13．12 14．60 15．25 16．3 17．（1）；（2）2三、解答题（共89分） 18.（本小题9分） 解：原式3413=+-+ ……………………………………………………………8分 9= ……………………………………………………………………… 9分 19．（本小题9分） 解：原式22469x x x =-+-+ …………………………………………………4分136x =- ………………………………………………………………6分当12x =-时，原式1136()2=-⨯- ………………………………………7分16= …………………………………………………9分20．（本小题9分）证明：∵AB AC =, ∴B C ∠=∠……………3分∵DE AB DF AC ，⊥⊥，∴90BED CFD ∠=∠=︒.…………………6分 ∵D 为BC 边的中点, ∴BD CD =, ……8分∴BED ∆≌CFD ∆. ………………………9分21．（本小题9分）解：（1）60，补图如右；（填空3分，补图2分，共5分） （2）由图可得：第四组的件数是18件，第六组的件数是3件，故第四组的获奖率为：105189=， 第六组的获奖率为：2639=,……………………8分 ∵5699<， ∴第六组获奖率较高. …………………………………………………………………9分22．（本小题9分） 解：（1）P （e 队出场）=13; …………………………………………………………3分 （2）解法一: 画树状图……………………6分由树状图可知，共有9种机会均等的情况，其中首场比赛出场的两个队都是县区学校队 的有4种情况， P ∴（两队都是县区队）=49. ………………………………………9分…………………6分由树状图可知，共有9种机会均等的情况，其中首场比赛出场的两个队都是县区学校队的有4种情况，P ∴（两队都是县区队）=49. ………………………9分 23．（本小题9分）解：（1）如图所示： …………………………3分 点B 的对应点'B 的坐标为（0，-6）； ……6分（2）第四个顶点D 的坐标()7,3-、()3,3、()5,3--； ……………………………………9分甲组 乙组 （第23题图）参赛作品件数条形统计图(第21题图)24．（本小题9分）解：（1）设甲种新款服装购进x 件，那么乙种新款服装购进(100)x -件，由题意可得 300500(100)42000x x +-=，解得40x =. ………………………………2分 经检验,符合题意.当40x =时，10060x -=(件).答：甲种新款服装购进40件，乙种新款服装购进60件.………………………………4分 （2）解法一：设甲种新款服装购进m 件，那么乙种新款服装购进(100)m -件，由题意可得1002m m -≤,解得1333m ≥.…………………………………………………………………6分∴m 的取值范围为1331003m ≤<.380300600500-<-∴同样售出一件新款服装,甲的获利比乙少,∴只能取34m =,此时获利为3480661009320⨯+⨯=（元）.答：甲种新款服装购进34件，乙种新款服装购进66件，才能使专卖店在销售完这批服装时获 利最多,最大利润为9320元. …………………………………………………9分 解法二：设该专卖店销售完这批服装可获利润w 元，甲种服装m 件.依题意可得，(380300)(600500)(1w m m =-+--, 整理得1000020w m =-. ∴w 是m 的一次函数，且200-<. ∴w 随m 的增大而减小.∵乙的数量不能超过甲的数量的2倍， ∴1002m m ≤﹣， 解得1333m ≥, …………………………………………………………6分∴m 的取值范围为1331003m ≤<.∵m 为整数，∴34m =时，w 取得最大值，此时9320w =（元）.答：该专卖店购进甲种服装34件，乙种服装66件，销售完这批服装时获利最多，此时利润为9320元．…………………………………………………………………………9分25．（本小题13分）解：（1）∵抛物线1C 的过点()0,1，∴()2103a =-，解得：19a =. ∴设抛物线1C 的解析式为()2139y x =-. …………3分(2) ①∵点A 、C 关于y 轴对称，∴点K 为AC 的中点.若四边形APCG 是平行四边形，则必有点K 是PG 的中点. 过点G 作GQ y ⊥轴于点Q ， 可得：GQK ∆≌POK ∆，∴3GQ PO ==，2KQ OK m ==， 22OQ m =. ∴点()23,2G m -. ……………………………5分 ∵顶点G 在抛物线1C 上，∴()2212339m =--，解得：m =0m >，∴m =∴当m =APCG 是平行四边形. ……………………………………8分 ②在抛物线()2139y x =-中，令2y m =，解得：33x m =±，又0m >，且点C 在点B 的右侧，∴()233,C m m +，33KC m =+. …………………………………………………9分 ∵点A 、C 关于y 轴对称， ∴()233,A m m --.∵抛物线1C 向下平移()0h h >个单位得到抛物线2C ， ∴抛物线2C 的解析式为：()2139y x h =--. ∴()2213339m m h =----，解得：44h m =+， ∴44PF m =+. ∴()()3133344414m KC m PF m m ++===++……………………13分(第25题图)26．（本小题13分） 解：（1）点G 的坐标是(0,2)；………………………3分 （2）解法一：①连结OP 、OB . ∵PB 切⊙O 于点B ， ∴OB PB ⊥；根据勾股定理得：222PB OP OB =﹣， ∵1OB =不变，若BP 要最小，则只须OP 最小.即当OP GF ⊥时，线段PO 最短，………………6分在Rt PFO ∆中，30OF GFO =∠=︒,∴OP∴PB =分 解法二：设直线GF 解析式为(0)y mx n m =+≠. ∵直线GF 过点(0,2)、F ()0,∴0,2n n ⎧+=⎪⎨=⎪⎩解得： 2.m n ⎧=⎪⎨⎪=⎩∴2y x =+.……………………………………………………………………………5分设(,2)P x +. 过P 作PH x ⊥轴于点H ,连结OA 、OP ,在Rt OHP ∆中,2222224(2)43OP OH PH x x =+=++=-+. PA 与⊙O 相切，∴90OAP ∠=︒,1OA =.在Rt PAO ∆中, 222AP OP OA =-. ∵PA PB 、均与⊙O 相切,∴222224413PB AP OP OA x ==-=+-22443(233x x =+=+. ∴当x =22PB =为最小， PB最小，此时PB = ………………………8分 ②方法一：存在．∵PA PB 、均与⊙O 相切， ∴OP 平分APB ∠. ∵60APB ∠=︒，∴30OPB ∠=︒. ∵1OB =， ∴2OP =.∴点P 是以点O 为圆心，2为半径的圆与直线GF 的交点，即图中的12P P 、两点. ∵2OG =，∴点1P 与点(0,2)G 重合.………………………………………………10分 在Rt GOF ∆中，30GFO ∠=︒，∴60OGF ∠=︒.∵2OG OP =，∴2GOP ∆是等边三角形, ∴2 2G P OG ==. ∵4GF =， ∴22FP =， ∴2P 为的中点GF ,∴2P . 综上所述，满足条件的点P 坐标为(0,2)或.……………………………………13分 方法二：假设在直线GF 上存在点P ，使得60APB ∠=︒，则必须有30APO ∠=︒. PA OA ⊥, 90OAP ∴∠=︒.∴1sin 2OA APO OP ∠==， ∴22OP OA ==. ……………………………………………………………………10分由①解法二可知22443OP x =+，∴224423x +=，解得10x =，2x . ∴满足条件的点P 坐标为(0,2)或. …………………………………13分(第26题图)。

2014年福建省泉州市中考数学试卷一、选择题（每小题有四个答案，其中有且只有一个答案是正确的，请在答题卡题目区域内作答答对的得3分，答错或不答一律得0分．）D．3．（3分）（2014•泉州）如图的立体图形的左视图可能是（）．C D．237．（3分）（2014•泉州）在同一平面直角坐标系中，函数y=mx+m与y=（m≠0）的图象可能是（）．C D．二、填空题(每小题4分，共40分）8．（4分）（2014•泉州）2014年6月，阿里巴巴注资1200000000元入股广州恒大，将数据1200000000用科学记数法表示为_________．9．（4分）（2014•泉州）如图，直线AB与CD相交于点O，∠AOD=50°，则∠BOC=_________°．5.方茴说：“那时候我们不说爱，爱是多么遥远、多么沉重的字眼啊。

我们只说喜欢，就算喜欢也是偷偷摸摸的。

”6.方茴说：“我觉得之所以说相见不如怀念，是因为相见只能让人在现实面前无奈地哀悼伤痛，而怀念却可以把已经注定的谎言变成童话。

”7.在村头有一截巨大的雷击木，直径十几米，此时主干上唯一的柳条已经在朝霞中掩去了莹光，变得普普通通了。

8.这些孩子都很活泼与好动，即便吃饭时也都不太老实，不少人抱着陶碗从自家出来，凑到了一起。

9.石村周围草木丰茂，猛兽众多，可守着大山，村人的食物相对来说却算不上丰盛，只是一些粗麦饼、野果以及孩子们碗中少量的肉食。

10．（4分）（2014•泉州）计算：+=_________．11．（4分）（2014•泉州）方程组的解是_________．12．（4分）（2014•泉州）在综合实践课上，六名同学的作品数量（单位：件）分别为：3、5、2、5、5、7，则这组数据的众数为_________件．13．（4分）（2014•泉州）如图，直线a∥b，直线c与直线a，b都相交，∠1=65°，则∠2=_________°．14．（4分）（2014•泉州）如图，Rt△ABC中，∠ACB=90°，D为斜边AB的中点，AB=10cm，则CD的长为_________ cm．15．（4分）（2014•泉州）如图，在△ABC中，∠C=40°，CA=CB，则△ABC的外角∠ABD=_________°．16．（4分）（2014•泉州）已知：m、n为两个连续的整数，且m＜＜n，则m+n=_________．17．（4分）（2014•泉州）如图，有一直径是米的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC，则：（1）AB的长为_________米；（2）用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为_________米．5.方茴说：“那时候我们不说爱，爱是多么遥远、多么沉重的字眼啊。

2014年福建省泉州市中考数学试卷一、选择题（每小题有四个答案，其中有且只有一个答案是正确的，请在答题卡题目区域内作答答对的得3分，答错或不答一律得0分．）1．（3分）（2014•泉州）2014的相反数是（）2．（3分）（2014•泉州）下列运算正确的是（）3．（3分）（2014•泉州）如图的立体图形的左视图可能是（）A．B．C．D．4．（3分）（2014•泉州）七边形外角和为（）5．（3分）（2014•泉州）正方形的对称轴的条数为（）6．（3分）（2014•泉州）分解因式x2y﹣y3结果正确的是（）7．（3分）（2014•泉州）在同一平面直角坐标系中，函数y=mx+m与y=（m≠0）的图象可能是（）．．二、填空题(每小题4分，共40分）8．（4分）（2014•泉州）2014年6月，阿里巴巴注资1200000000元入股广州恒大，将数据1200000000用科学记数法表示为．9．（4分）（2014•泉州）如图，直线AB与CD相交于点O，∠AOD=50°，则∠BOC=°．10．（4分）（2014•泉州）计算：+=．11．（4分）（2014•泉州）方程组的解是．12．（4分）（2014•泉州）在综合实践课上，六名同学的作品数量（单位：件）分别为：3、5、2、5、5、7，则这组数据的众数为件．13．（4分）（2014•泉州）如图，直线a∥b，直线c与直线a，b都相交，∠1=65°，则∠2= °．14．（4分）（2014•泉州）如图，Rt△ABC中，∠ACB=90°，D为斜边AB的中点，AB=10cm，则CD的长为cm．15．（4分）（2014•泉州）如图，在△ABC中，∠C=40°，CA=CB，则△ABC的外角∠ABD= °．16．（4分）（2014•泉州）已知：m、n为两个连续的整数，且m＜＜n，则m+n=．17．（4分）（2014•泉州）如图，有一直径是米的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC，则：（1）AB的长为米；（2）用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为米．三、解答题（共89分）18．（9分）（2014•泉州）计算：（2﹣1）0+|﹣6|﹣8×4﹣1+．19．（9分）（2014•泉州）先化简，再求值：（a+2）2+a（a﹣4），其中a=．20．（9分）（2014•泉州）已知：如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．21．（9分）（2014•泉州）在一个不透明的箱子里，装有红、白、黑各一个球，它们除了颜色之外没有其他区别．（1）随机地从箱子里取出1个球，则取出红球的概率是多少？（2）随机地从箱子里取出1个球，放回搅匀再取第二个球，请你用画树状图或列表的方法表示所有等可能的结果，并求两次取出相同颜色球的概率．22．（9分）（2014•泉州）如图，已知二次函数y=a（x﹣h）2+的图象经过原点O（0，0），A（2，0）．（1）写出该函数图象的对称轴；（2）若将线段OA绕点O逆时针旋转60°到OA′，试判断点A′是否为该函数图象的顶点？23．（9分）（2014•泉州）课外阅读是提高学生素养的重要途径．某校为了了解学生课外阅读情况，随机抽查了50名学生，统计他们平均每天课外阅读时间（t小时）．根据t的长短分为A，B，C，D四类，下面是根据所抽查的人数绘制的两幅不完整的统计图表．请根据图中提供的信息，解答下面的问题：50名学生平均每天课外阅读时间统计表（1）求表格中的a的值，并在图中补全条形统计图；（2）该校现有1300名学生，请你估计该校共有多少名学生课外阅读时间不少于1小时？24．（9分）（2014•泉州）某学校开展“青少年科技创新比赛”活动，“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型．甲、乙两车同时分别从A，B出发，沿轨道到达C处，在AC上，甲的速度是乙的速度的1.5倍，设t（分）后甲、乙两遥控车与B 处的距离分别为d1，d2，则d1，d2与t的函数关系如图，试根据图象解决下列问题：（1）填空：乙的速度v2=米/分；（2）写出d1与t的函数关系式；（3）若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰，试探求什么时间两遥控车的信号不会产生相互干扰？25．（12分）（2014•泉州）如图，在锐角三角形纸片ABC中，AC＞BC，点D，E，F分别在边AB，BC，CA上．（1）已知：DE∥AC，DF∥BC．①判断四边形DECF一定是什么形状？②裁剪当AC=24cm，BC=20cm，∠ACB=45°时，请你探索：如何剪四边形DECF，能使它的面积最大，并证明你的结论；（2）折叠请你只用两次折叠，确定四边形的顶点D，E，C，F，使它恰好为菱形，并说明你的折法和理由．26．（14分）（2014•泉州）如图，直线y=﹣x+3与x，y轴分别交于点A，B，与反比例函数的图象交于点P（2，1）．（1）求该反比例函数的关系式；（2）设PC⊥y轴于点C，点A关于y轴的对称点为A′；①求△A′BC的周长和sin∠BA′C的值；②对大于1的常数m，求x轴上的点M的坐标，使得sin∠BMC=．2014年福建省泉州市中考数学试卷参考答案与试题解析一、选择题（每小题有四个答案，其中有且只有一个答案是正确的，请在答题卡题目区域内作答答对的得3分，答错或不答一律得0分．）3．（3分）（2014•泉州）如图的立体图形的左视图可能是（）．．237．（3分）（2014•泉州）在同一平面直角坐标系中，函数y=mx+m与y=（m≠0）的图象可．．的图象可知的图象可知二、填空题(每小题4分，共40分）8．（4分）（2014•泉州）2014年6月，阿里巴巴注资1200000000元入股广州恒大，将数据1200000000用科学记数法表示为 1.2×109．9．（4分）（2014•泉州）如图，直线AB与CD相交于点O，∠AOD=50°，则∠BOC=50°．10．（4分）（2014•泉州）计算：+=1．=111．（4分）（2014•泉州）方程组的解是．，则方程组的解为故答案为：12．（4分）（2014•泉州）在综合实践课上，六名同学的作品数量（单位：件）分别为：3、5、2、5、5、7，则这组数据的众数为5件．13．（4分）（2014•泉州）如图，直线a∥b，直线c与直线a，b都相交，∠1=65°，则∠2= 65°．14．（4分）（2014•泉州）如图，Rt△ABC中，∠ACB=90°，D为斜边AB的中点，AB=10cm，则CD的长为5cm．CD=CD=AB=15．（4分）（2014•泉州）如图，在△ABC中，∠C=40°，CA=CB，则△ABC的外角∠ABD= 110°．16．（4分）（2014•泉州）已知：m、n为两个连续的整数，且m＜＜n，则m+n=7．估算出＜题考查的是估算无理数的大小，先根据题意算出的取值范围是解答此题的关17．（4分）（2014•泉州）如图，有一直径是米的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC，则：（1）AB的长为1米；（2）用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为米．r=，然后解方程即可．AB=r=．．三、解答题（共89分）18．（9分）（2014•泉州）计算：（2﹣1）0+|﹣6|﹣8×4﹣1+．×+419．（9分）（2014•泉州）先化简，再求值：（a+2）2+a（a﹣4），其中a=．时，）20．（9分）（2014•泉州）已知：如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．21．（9分）（2014•泉州）在一个不透明的箱子里，装有红、白、黑各一个球，它们除了颜色之外没有其他区别．（1）随机地从箱子里取出1个球，则取出红球的概率是多少？（2）随机地从箱子里取出1个球，放回搅匀再取第二个球，请你用画树状图或列表的方法表示所有等可能的结果，并求两次取出相同颜色球的概率．个球，则取出红球的概率是：∴两次取出相同颜色球的概率为：=22．（9分）（2014•泉州）如图，已知二次函数y=a（x﹣h）2+的图象经过原点O（0，0），A（2，0）．（1）写出该函数图象的对称轴；（2）若将线段OA绕点O逆时针旋转60°到OA′，试判断点A′是否为该函数图象的顶点？OA B=，则﹣++OB=B=OB=）（）的顶点坐标为（﹣，﹣，＜﹣时，＞﹣时，﹣取得最小值时，时，﹣最大值23．（9分）（2014•泉州）课外阅读是提高学生素养的重要途径．某校为了了解学生课外阅读情况，随机抽查了50名学生，统计他们平均每天课外阅读时间（t小时）．根据t的长短分为A，B，C，D四类，下面是根据所抽查的人数绘制的两幅不完整的统计图表．请根据图中提供的信息，解答下面的问题：（1）求表格中的a的值，并在图中补全条形统计图；（2）该校现有1300名学生，请你估计该校共有多少名学生课外阅读时间不少于1小时？×=52024．（9分）（2014•泉州）某学校开展“青少年科技创新比赛”活动，“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型．甲、乙两车同时分别从A，B出发，沿轨道到达C处，在AC上，甲的速度是乙的速度的1.5倍，设t（分）后甲、乙两遥控车与B 处的距离分别为d1，d2，则d1，d2与t的函数关系如图，试根据图象解决下列问题：（1）填空：乙的速度v2=40米/分；（2）写出d1与t的函数关系式；（3）若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰，试探求什么时间两遥控车的信号不会产生相互干扰？；时，两遥控车的信号不会产生相互干扰；时，两遥控车的信号不会产生相互干扰0时，两遥控车的信号不会产生相互干扰．25．（12分）（2014•泉州）如图，在锐角三角形纸片ABC中，AC＞BC，点D，E，F分别在边AB，BC，CA上．（1）已知：DE∥AC，DF∥BC．①判断四边形DECF一定是什么形状？②裁剪当AC=24cm，BC=20cm，∠ACB=45°时，请你探索：如何剪四边形DECF，能使它的面积最大，并证明你的结论；（2）折叠请你只用两次折叠，确定四边形的顶点D，E，C，F，使它恰好为菱形，并说明你的折法和理由．AG==12AH=12==h=﹣AH=1226．（14分）（2014•泉州）如图，直线y=﹣x+3与x，y轴分别交于点A，B，与反比例函数的图象交于点P（2，1）．（1）求该反比例函数的关系式；（2）设PC⊥y轴于点C，点A关于y轴的对称点为A′；①求△A′BC的周长和sin∠BA′C的值；②对大于1的常数m，求x轴上的点M的坐标，使得sin∠BMC=．y=，因此点y=的图象上，y=．B=3，C=3+2BC O=A3=3CD=．3+2的值为．==．BMC=，BMC=．．的坐标为（的坐标为（﹣MH=═OH=EG=MH=﹣+（﹣（﹣的坐标为（）和（﹣的坐标为（（﹣（﹣联想到点。

2014年洛江区初中学业质量检查数 学 试 卷（试卷满分：150分；考试时间：120分钟）一、选择题（每小题3分，共21分）在答题卡上相应题目的答题区域内作答. 1. 下列各数中，比﹣1小的数是（ ）A.0B.2-C.21D. 1 2. 下列计算正确的是（ ）A. 326a a a =÷B.523)(a a =C. 525±=D. 283-=-3．不等式组⎩⎨⎧>-≥-02401x x 的解集在数轴上表示为（ ）．4. 为了解某小区“全民健身”活动的开展情况，随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计，结果如下表：这A ．4小时B ．4.5小时C ．5小时D ．5.5小时5. 如图CD 是Rt △ABC 斜边上的高，AC =4，BC =3， 则cos ∠BCD 的值是（ ）． A ．54 B ．43 C ．34 D ．536. 如图是由四个大小相同的正方体组合而成的几何体，其主视图是（ ）A ． Ｂ． Ｃ． Ｄ．7. 如图所示，半径为1的圆和边长为3的正方形在同一水平线上，圆沿该水平线从左向右匀速穿过正方形，设穿过时间为t ，正方形除去圆部分的面积为S （阴影部分），则S 与t 的大致图象为（ ）A． B．C ．D ．A ．B ．C ．D ．二、填空题（每小题4分，共40分）在答题卡上相应题目的答题区域内作答. 8.3-的相反数是 . 9.分解因式：_________642=-m .10. 我国南海海域的面积约为36000002km ，将3600000用科学记数法应表示为 . 11.计算：=-+-aa a 222 . 12. 已知点G 是△ABC 的重心，AG=8，那么点G 与边BC 中点之间的距离是 . 13. 已知一个多边形的每一个内角都等于108°，则这个多边形的边数是 . 14. 如图，在Rt △ABC 中，∠C =90°，作AB 的垂直平分线，交AB 于D ，交AC 于E ，连结BE ．已知∠CBE =40°，则∠A = 度．15. 当宽为3cm 的刻度尺的一边与圆相切时，另一边与圆的两个交点处的读数如图所示（单位：cm ），那么该圆的半径为 cm ．16. 如图，在正方形ABCD 中，E 是AB 上一点，BE=2，AE=3BE ，P 是AC 上一动点，则PB+PE 的最小值是 ．17.边长分别为2㎝、3㎝、5㎝的三个正方形如图排列，则线段EN= ㎝，阴影部分的面积= cm 2.三、解答题（共89分）在答题卡上相应题目的答题区域内作答.18.（9分）计算：()︒--+-⎪⎭⎫ ⎝⎛-60tan 2183101π.19.（9分）先化简，后求值：)1)(1()1(-+-+a a a a ，其中3=a .20.（9分）如图，已知四边形ABCD 是菱形，DE ⊥AB ，DF ⊥BC ，求证：△ADE ≌△CDF ．21.（9分）一个不透明的布袋里装有3个球，其中2都相同．（1）求摸出1个球是白球的概率；（2）摸出1个球，记下颜色后放回，并搅均，再摸出1个球．求两次摸出的球恰好颜色不同的概率（要求画树状图或列表）．22．（9分）如图，一次函数y=kx+b （k ≠0）的图象与反比例函数xmy =（m ≠0）的图象交于二、四象限内的A 、B 两点，与x 轴交于C 点，点B的坐标为（6，n ）．线段OA =5，E 为x 轴上一点，且sin∠AOE =54． （1）求该反比例函数和一次函数的解析式； （2）求△AOC 的面积．23.（9分）小张同学学完统计知识后，随机调查了她所在辖区若干名居民的年龄，将调查数据绘制成如下扇形统计图和条形统计图：请根据以上不完整的统计图提供的信息，解答下列问题：（1）小张同学共调查了 名居民的年龄，扇形统计图中a ＝ %； （2）补全条形统计图，并注明人数；（3）若在该辖区中随机抽取一人，那么这个人年龄是60岁及以上的概率为 ； （4）若该辖区年龄在0～14岁的居民约有3500人，请估计该辖区居民人数是 人.24.（9分）大润发超市进了一批成本为8元/个的文具盒．调查发现：这种文具盒每个星期的销售量y （个）与它的定价x （元/个）的关系如图所示：（1）求这种文具盒每个星期的销售量y （个）与它的定价x （元/个）之间的函数关系式（不必写出自变量x 的取值范围）；（2）每个文具盒定价是多少元时，超市每星期销售这种文具盒（不考虑其他因素）可获得的利润最高？最高利润是多少？25．（13分）如图，抛物线x x my 222-=与x 轴的负半轴交于点A ，对称轴经过顶点B 与x 轴交于点M .第23题图（1）求抛物线的顶点B 的坐标 (用含m 的代数式表示)； （2）连结BO ，若BO 的中点C 的坐标为(23-，23)， 求抛物线的解析式； （3）在（2）的条件下，D 在抛物线上，E 在直线 BM 上，若以A 、C 、D 、E 为顶点的四边形是平行四边形，求点D 的坐标.26.（13分）已知： M 点是等边三角形△ABC 中BC 边上的中点，也是等边△DEF 中EF 边上的中点，连结AD .（1）如图1，当EF 与BC 在同一条直线上时，直接写出BEAD的值； （2）如图2，△ABC 固定不动，将图1中的△DEF 绕点M 顺时针旋转α（o 0≤α≤o 90）角， ①判断（1）中的结论是否仍然成立，若成立，请加以证明；若不成立，说明理由； ②作DH ⊥BC于点H ．设BH ＝x ，线段AB ，BE ，ED ，DA 所围成的图形面积为S ．当2014年洛江区初中学业质量检查数学试题参考答案及评分标准一、选择题（每小题3分，共21分）1.B2.D ；3.D ；4.C ；5.A ；6.D ；7.A. 二、填空题（每小题4分，共40分）8. 3； 9.()()88-+m m 10. 6106.3⨯ 11. 1 12. 4 ；图2备用图图113. 5； 14.25； 15.62516.10； 17.2.5，3.75 三、解答题（共89分）18.（9分）解：()︒--+-⎪⎫ ⎝⎛-60tan 2183101π.31=--………………8分4=-9分19.（9分）解：原式=)1(22--+a a a ………………4分=122+-+a a a …………………5分 =1+a ………………………………6分 当3=a 时，原式=3+1=4．……………9分20.（9分）证明：在△ADE 和△CD F 中， ∵四边形ABCD 是菱形， ∴∠A =∠C ，AD =CD ， …………4分 又DE ⊥AB ，DF ⊥BC ， ∴∠AED =∠CFD =90°，…………6分∴△ADE ≌△CDF ．……………9分21.（9分）解：（1）31……………………………………………………3分解：（1）过点A 作AD ⊥x 轴于D 点，如图，∵sin ∠AOE =AO AD =54，OA =5，∴AD =4，………………………………1分∴DO = 34522=-，………………2分而点A 在第二象限，∴点A 的坐标为（-3，4），将A （-3，4）代入xmy =，得m =-12，∴反比例函数的解析式为y=x12- ；…………3分开始将B （6，n ）代入y=x12-，得n = -2；…………4分 将A （-3，4）和B （6，-2）分别代入y=kx+b （k ≠0），得⎩⎨⎧-=+=+-2643b k b k ……………5分 解得⎪⎩⎪⎨⎧=-=232b k ， ∴所求的一次函数的解析式为232+-=x y ；…………6分（2）在232+-=x y 中，令0=y ，得3=x ，∴C 点坐标为（3，0），即OC =3，……………………7分∴6342121=⨯⨯=⋅⋅=∆OC AD S AOC ．……………9分23.（9分）（1）500；20%；………… 2分 （2）110，图略；…………… 4分（3）12% ………………6分 （4）17500. ……………9分24.（9分）解：（1）设y=kx+b ……………………1分 由题意得：⎩⎨⎧=+=+1601420010b k b k ，………………………2分解之得：⎩⎨⎧=-=30010b k ……………………………………3分∴y =﹣10x+300．……………………………………4分 （2）设超市每星期的总利润为w 元， 则W =（x ﹣8）•y =（x ﹣8）（﹣10x +300）………………6分 =﹣10（x ﹣8）（x ﹣30）=﹣10x 2+380x -2400=﹣10（x ﹣19）2+1210………………………………8分答：当x =19即定价19元/个时超市可获得的利润最高，最高利润为1210元．……9分25．（13分） 解：（1）∵22222221212112()()4422y x x x mx m m x m m m m m m =-=-+-⋅=--， ∴抛物线的顶点B 的坐标为11(,)22m m -.（2）作⊥CN x 轴于点N ，∵C (23-，23)是BO 的中点，∴CN 是BMO ∆的中位线∴BM=3………………………………5分 即B 的纵坐标为3，由321=-m 得 6-=m∴ 抛物线的解析式为2123y x x =--. …………7分 （3）令0=y ，得61-=x ，02=x ∴A (-6,0)由点D 在抛物线2123y x x =--上，设D (t ，(ⅰ)当AC 为所求平行四边形的一边时 如右图，过C 作CF ⊥ x 轴于F ,过D 1作D 1H ⊥ BE 于H , 则23-==C F x x , 3-==B H x x .由四边形ACD 1E 1为平行四边形， 可证△ACF ≌△D 1E 1H .可得D 1H = AF =4.5 ∴ t -(-3)=4.5∴ t =23∴)415,23(1-D . ……………… 如右图，同 方法可得 D 2H=AF =4.5.∴ -3- t =4.5 ∴ t =-7.5 ∴)415,215(2--D . ……………………11(ⅱ)当AC 为所求平行四边形的对角线时如右图，过C 作CF ⊥BM 于F 过D 3作D 3H ⊥ x 轴于H , 则则3-==B F x x , t x x D H ==3.由四边形AE 3CD 3为平行四边形， 可证△AD 3H ≌△CE 3F .可得AH = CF =23.∴ t -(-6)= 23.∴ t =29-.∴)49,29(3-D . …………………………13分综上，点D 的坐标为)415,23(1-D ,)415,215(2--D ,)49,29(3-D 26．（13分）解：（1）ADBE=3分 （2）① (1)中结论仍成立；证明：连接DM ，AM ．在等边三角形ABC 中，M 为BC 的中点，∴ AM BC ⊥，1302BAM BAC ∠=∠=︒，AMBM∴ 90BME EMA ∠+∠=︒．………………5分同理，DMEM=，90AMD EMA ∠+∠=︒． ∴AM DMBM EM=，AMD BME ∠=∠． ∴ △ADM ∽△BEM ．∴AD DM BE EM= …………………………8分② ∵ △ADM ∽△BEM ，∴2()3ADM BEM S AD S BE∆∆==．…………………………9分 ∴ 13BEM ADM S S ∆∆=∴ ABM ADM BEM DEM S S S S S ∆∆∆∆=+--…………10分23ABM ADM DEM S S S ∆∆∆=+-121133)12322x =⨯⨯⨯⨯--⨯=12分∴S =（3≤x≤3+）……………13分四、附加题1. 62. o 130。

泉港区2014年初中学业质量检测数 学 试 题（满分：150分 考试时间：120分钟）一、选择题（每小题3分，共21分）1．2-的相反数是…………………………………………………………………………（ ）A ．2-B ．2C ．12D ．12-2.下列各式的运算正确的是………………………………………………………………（ ） A ．9)3(2-=-B ．2323-=÷- C ．523)(a a = D ．65632a a a =⋅ 3．如图是由4个相同的正方体组成的几何体，则这个几何体的俯视图是………………（ ）4. 已知⊙O 1与⊙O 2相内切，它们的半径分别是3，5.则圆心距O 1O2为……………（ ） A ．15B ． 8D C ． 4 D ． 25.已知3x =是关于x 的方程062=-+kx x 的一个根，则另一个根是………………（ ）A ．=x 1B ．=x －1C ．=x －2D ．=x 26.四边形ABCD 中，AC 、BD 相交于点O ，不能判定它是平行四边形的条件是………（ ） A ．AB ∥CD ，AD ∥BC B ．AO ＝CO ，BO ＝DOC ．AB ∥CD ，AD ＝BC D ．AB ＝CD ，AD ＝BC 7．如图，在轴的正半轴与射线上各放置着一平面镜，发光点（0，1）处沿如图所示方向发射一束光，每当碰 到镜面时会反射（反射时反射角等于入射角），当光线第30次碰到镜面时的坐标为（ ）A ．（30，3）B ．（88，3）C ．（30，0）D ．（88，0）二、填空题（每题4分，共40分）．8．据统计今年我省约有255000人报名参加高考，请将数据255000用科学记数法表示： ． 9．不等式组⎩⎨⎧>-≤-06312x x的解集是 ．A B C D10．分解因式：=-362a ．11．今年体育学业考试立定跳远项目测试时，某记录员记录一组五位同学的成绩（单位：米）分别是：1.3，2.2，2.0，1.8，1.6 ,则这组数据的中位数是 . 12．正n 边形的一个外角等于40°.则n ＝ ． 13. 计算：=-+-ab bb a a . 14．如图，AC ⊥BC 于点C ，DE ⊥BE 于点E ，BC 平分∠ABE ，∠BDE ＝58°．则∠A ＝ 度.15.如图，在菱形ABCD 中，2=AB ，︒=∠60A ．则菱形ABCD 的面积=S .16．小李和小陆沿同一条路行驶到B 地，他们离出发地的距离S 和行驶时间t 之间的函数关系的图象如图所示．已知小李离出发地的距离S 和行驶时间t 之间的函数关系为102+=x y ．则①小陆离出发地的距离S 和行驶时间t 之间的函数关系为： ；②他们相遇的时间=t ．17．如图，矩形ABCD 中，3=AB ，4=BC ,点E 是BC 边上一点，把B ∠沿AE 折叠，使点B 落在点'B 处，则①='B A ；②当△'CEB 为直角三角形时，BE ＝ ．三、解答题（共89分）．18.（9分）计算：)2()2()2014(21852501-⨯-+--÷-⨯-π19.（9分）先化简，再求值：)42(2)2(2+-+x x ，其中2=x ．20.（9分）如图，四边形ABCD 中，AD ＝CD ，连结BD ．若不增加任何字母与辅助线，（第14图）A B （第17图） E A B C DB '（第15图）BC D )（第16图）要使△ABD ≌△CBD ，则还需增加一个条件是 ，并给予证明．21．（9分）记者小张要了解市民对“雾霾天气产生的主要成因”的看法，随机调查了某区的部分市民，并绘制了如下不完整的统计图表．请根据提供的信息解答下列问题： （1）填空：m = ，n = ；（2）请求扇形统计图中E 选项所占的百分比为 ；（3）若该区人口约有40万人，请估计其中持D 选项“观点”的市民人数有多少人？选项 观点 频数（人数）A 大气气压低，空气不流动 80B 地面灰尘大，空气湿度低m C 汽车尾气排放n D 工厂造成的污染 120 E 其他 6022．（9分）一个不透明的口袋里装有分别标有汉字“石”、“化”、“新”、“城”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球． （1）若从袋中任取一个球，球上的汉字刚好是“新”的概率为多少？（2）小明从袋中任取一球后，再任取一球，请用树状图或用列表的方法求出取出的两个球上的汉字能组成“石化”或“新城”的概率．23．（9分）如图，正方形ABCD 的顶点B 与⊙O 的圆心O 的重合，点A 在⊙O 上，CD ＝6cm ．将正方形ABCD 向右平移运动，当点B 到达⊙O 上时运动停止．设正方形ABCDC DA B C A BDE 00200010与⊙O 重叠部分（阴影部分）的面积为S ． （1）请写出⊙O 半径的长度；（2）试写出正方形ABCD 平移运动过程中，S 的大小变化规律；（3）在平移过程中，AD 、BC 与⊙O 的交点分别为E 、F ．当EF ＝6cm 时，求S 的值．24．（9分）“六一”节前，A 商店购进一批儿童衣服．若每件60元卖出，盈利率为20%． （1）请求出这批儿童的进价；（2）A 商店在试销售这种衣服时，决定每件售价不低于进价，又不高于每件70元．已知试销中销售量y （件）与销售单价x (元)的关系为100+-=x y ．问当销售单价定为多少元时，商店销售这种衣服的利润最大？（00100⨯-=进价进价售价盈利率）25．（13分）如图，一次函数b ax y +=与反比例函数xy 2-=的图象交于A 、B 两点．过 A 点分别作x 轴、y 轴的垂线，E 、F 为垂足． （1）请直接写出矩形AEOF 的面积；（2）设一次函数b ax y +=与x 轴、y 轴的交点分别为C 、D ，当OE OC 3=时．A①试求OCD ∆的面积；②当1=OE 时，以BD 为直径作⊙N ，与x 轴相交于P 点，请求出P 点的坐标．26．（13分）如图，抛物线1C ：42++=bx ax y 的图象与两坐标轴分别交于C B A 、、三点，经过点E （0，2-）的直线l ：()02≠-=k kx y 与x 轴、抛物线的对称轴1-=x 交于点F ．（1）填空：=OC ；=OF ；（2）连结AE ．若OAE ∆∽OEF ∆，请求出抛物线1C 的解析式； （3）在（2）的条件下，把抛物线1C 向右平移1个单位后，向下平移29个单位得到新的抛物线2C ．再将直线l 绕着点E 进行旋转，当直线l 与抛物线2C 相交于不同的两个交点N M 、时，过点P （0，2）、点M 与点N 分别作直线PN PM 、．猜想：直线PN PM 、、CE 之间的位置关系（除相交于点P 外）．并请说明理由．泉港区2014年初中学业质量检测数学参考答案及评分标准一、选择题（每小题3分，共21分）1．B ； 2．D ； 3．A ； 4．D ； 5．C ； 6．C ； 7．B ； 二、填空题（每小题4分，共40分）8．51055.2⨯； 9．x ≤2； 10．)6)(6(-+x x ； 11．1.8； 12．9； 13．1； 14．58°； 15．32； 16．①x y 10=，②45； 17．①3；②332或． 三、解答题（共89分）18.（9分）解：原式＝4135+-- ……………………………………………………………………………8分＝5 ………………………………………………………………………………………9分 19．（9分）解：原式84442--++=x x x ………………………………………………………………4分42-=x …………………………………………………………………………………6分当x＝2时，4)2(422-=-x ………………………………………………………………7分＝2- ………………………………………………………………………9分 20．（9分）解：答案不惟一，如：AB ＝DC 或∠ADB ＝∠BDC 等．证明： AB ＝BC ………………………………………………………………………………………3分在△ABD 和△CBD 中，⎪⎩⎪⎨⎧===BD BD CB AB CD AD ……………………………………………………………………………6分 ∴△ABD ≌△CBD(SAS) ………………………………………………………………………9分 21．（9分）解：（1）填空：m =40，n =100…………………………………………………………………4分 （2）8020%400÷=E组所占百分比是604000.1515%÷==…………………………………………………………6分 （3）持D 选项“观点”的市民所占的百分比为：1204000.330%÷==…………………………7分 ∴12304000=⨯ （万人）答：估计该区持D 选项“观点”的市民人数12万人．………………………………………………9分22.（9分）解：（1）任取一个球是“新”的概率为41； ………………………………………………… 3分 （2）方法一（画树状图法）：第1颗球……………… 3分……………… 7分石 化 新 城石 新 城 石 化 城 石 化 新∵12种可能的结果中，能组成“石化”、“新城”各有2种可能. ……………………………… 8分∴31124= ∴取出的两个球上的汉字恰能组成“石化”或“新城”的概率是31. …………………………… 9分 23．（9分）解：(1)⊙O半径cm OA 6=……………………………………………………………………… 3分(2) 正方形ABCD 平移运动过程中，S 的大小变化规律是先变大后变小……………… 5分(3) ∵cm EF cm OF cm OE 6,6,6===∴是等边三角形OEF ∆ ……………………………………………………………… 6分∴︒=∠60EOF ………………………………………………………………………… 7分∴︒⨯⨯+⨯=60sin 66213606602πS ………………………………………………… 8分396+=π即 当6=EF 时， 396+=πS(2cm )………………………………………………… 9分24.（9分）解：（1）设购进这种衣服每件需a 元，依题意得：6020%a a -= ……………………………………………………………………………………2分解得：50a = ………………………………………………………………………………………3分答：购进这种衣服每件需50元 ……………………………………………………………………4分（2）利润为(5x x ω=--+………………………………………………………………………6分 21505000x x =-+-第2颗球＝2(75)625x --+ ……………………………………………………………………………7分∵函数2(75)625x ω=--+的图像开口向下，对称轴为直线75x =,∴当5070x ≤≤时，ω随x的增大而增大，………………………………………………………………8分∴当70x =时，600ω=最大.答：当销售单价定为70元时，商店销售这种衣服的利润最大……………………………………………9分 25．（13分）解：（1）2 …………………………………………………………………………………… 3分（2）设OE= m (m >0).则E(-m ,0), C(3m ,0), A(-m ,m2)AE ⊥x 轴、AF ⊥y 轴 ∴∠AEC =∠DOC =90° 又∵∠ACE =∠DCO∴△AEC ∽△DOC∴CEOCAE OD = ∴mAE CE OC OD 43=⋅=……………………………………………………………………………7分∴294332121=⋅⋅=⋅=∆m m OD OC S OCD …………………………………………………………8分（3）过点N 作NG ⊥y 轴于点G ，过点B 作BH ⊥y 轴于点H ，过点N 作NM ⊥x 轴于点M .当1=OE 时，得A (-1,2), C (3，0) 代入b ax y +=，得⎩⎨⎧=+=+-032b a b a解得 21-=a ，23=b ∴2321+-=x y ………………………………………………………………………………………9分由A 、B 两点在一次函数b ax y +=与反比例函数y 2-=的图象上xx 22321-=+-解得11-=x ，42=x 当11-=x 时，21=y 当42=x 时，212-=y ∴点B (4，21-)………………………………………………………………………………………10分 则直线2321+-=x y 与y 轴于点D (0，23)∴在BDH Rt ∆中，52422222=+=+=BH DH BD∵NG ⊥y 轴，BH ⊥y 轴 ∴NG ∥BH 又∵DN =BN∴DG =HG , 221==BH NG ∵点N 在直线2321+-=x y∴点)21,2(N ……………………………………………………………………………………………11分∴PMN Rt ∆中，419222=-=MN NP PM219=PM ……………………………………………………………………………………………12分∴P点的坐标为（2192-，0）或（2219+，0）……………………………………………13分 26. （13分）解：（1）4；1……………………………………………………………………………… 2分（2）∵E （0，2-），()02≠-=k kx y 与抛物线的对称轴1-=x 交于点F ∴OE =2，OF =1. …………………………………………………………………………………… 3分∵OAE ∆∽OEF ∆OFOEOE OA = ………………………………………………………………………………………… 4分∴OA =4 即A (-4，0)，B (2，0) …………………………………………………………………………… 5分代入42++=bx ax y 可解得1,21-=-=b a ………………………………………………… 6分∴4212+--=x x y (7)分（3）直线PN PM 、关于直线CE 成轴对称。