2017届山东省实验中学高三第二次模拟考试理科数学试题及答案 精品
- 格式:doc
- 大小:1.35 MB
- 文档页数:11

2024-2025学年吉林省松原市宁江区实验高级中学高三年级第二次调研考试英语试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
第一部分(共20小题,每小题1.5分,满分30分)1.Tourists love Beijing, offers an infinite collection of delights ranging from 6 UNESCO World Heritage Sites to food from every corner of China and beyond.A.that B.whereC.which D.who2.—When ______ leave for Japan?—When ______ leave for Japan is kept secret.”A.they will, will they B.will they, they willC.they will, they will D.will they, will they3.In order to make my composition clearer and smoother, my teacher asked me to _________ the unnecessary words and sentences.A.leave alone B.leave behindC.leave off D.leave out4.It is obvious to the students _____________they should get well prepared for their future.A.as B.thatC.which D.whether5.These remarkable findings suggest the elephants have ________ a memory capacity to make distinctions between human voices.A.built up B.packed up C.brought up D.took up6.Jane’s pale face suggested that she ______ ill and her parents suggested that she ______ a medical exam.A.be; should have B.was; haveC.should be; had D.was; had7.If you want to lead a happy life, you’d better learn to accep t life ______ it is.A.as B.thatC.which D.where8.I believed him to be honest but his actions showed that he had ________.A.the top dog B.the feet of clayC.his cup of tea D.the apple of his eye9.If it had not been for the heroes’ contributions an d sacrifices, we _____such a happy life.A.wouldn’t have led B.wouldn’t be leadingC.haven’t led D.are not leading10.— What great changes have taken place in our city in the last few years!— Indeed, many high buildings have _______all over the city.A.wound up B.sprung up C.held up D.made up11.We’d better go now, ______ we’ll miss the train.A.but B.so C.otherwise D.therefore12.President Xi underlines that it is only with joint efforts to keep maritime peace ________ build a maritime community with a shared future for mankind.A.can we B.we can C.that we can D.that can we13..When he goes out, he often wears sunglasses _______nobody can recognize him.A.so that B.now that C.in case D.as though14.If you want to see a doctor,you fix a date with him ahead of time.That is a common ________ in the USA.A.view B.exerciseC.practice D.reality15.It’s natural that I didn’t recognize her immediately I saw her. _______, it’s almost 5 years since we met last. A.After all B.In addition C.What’s more D.In particular16.Smell the flowers before you go to sleep, and you may just ________sweet dreams.A.keep up with B.put up with C.end up with D.catch up with17.He has made little preparation for the interview, so the chance of him succeeding in it is .A.slim B.fantasticC.obvious D.gentle18.The teacher spoke so fast that it was hard for the students to ______ what he was saying.A.take in B.take off C.take on D.take after19.---How was your evening?---We went to Joe’s and had ____. We really enjoyed ourselves.A.a white elephant B.a square meal C.a sacred cow D.the salt of the earth20..---Would you have told him the answer had it been possible?.---I would have, but I _____ so busy then.A.had been B.were C.was D.would be第二部分阅读理解(满分40分)阅读下列短文,从每题所给的A、B、C、D四个选项中,选出最佳选项。

山东省实验中学2024届高三调研考试数学试题2024.2说明:本试卷满分150分.试题答案请用2B 铅笔和0.5mm 签字笔填涂到答题卡规定位置上,书写在试题上的答案无效.考试时间120分钟.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.设{}{}21,4,2,1,A x B x ==,若B A ⊆,则x =()A.0B.0或2C.0或2- D.2或2-2.若22nx ⎫⎪⎭展开式中只有第6项的二项式系数最大,则n =()A.9B.10C.11D.123.已知向量()()1,3,2,2a b ==,则cos ,a b a b +-= ()A.117B.17C.55D.2554.等差数列{}n a 的首项为1,公差不为0,若236,,a a a 成等比数列,则{}n a 前6项的和为()A.24- B.3- C.3D.85.要得到函数cos 2y x =的图象,只需将函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图象沿x 轴A.向左平移12π个单位 B.向左平移6π个单位C.向右平移6π个单位 D.向右平移12π个单位6.在三棱锥-P ABC 中,点M,N 分别在棱PC,PB 上,且13PM PC =,23PN PB =,则三棱锥P AMN -和三棱锥-P ABC 的体积之比为()A.19B.29C.13D.497.为研究某池塘中水生植物的覆盖水塘面积x (单位:2dm )与水生植物的株数y (单位:株)之间的相关关系,收集了4组数据,用模型e (0)kx y c c =>去拟合x 与y 的关系,设ln ,z y x =与z 的数据如表格所示:得到x 与z 的线性回归方程2ˆˆ 1.z x a=+,则c =()x3467z22.54.57A.-2B.-1C.2e -D.1e -8.双曲线2222:1(0,0)x y M a b a b-=>>的左、右顶点分别为,A B ,曲线M 上的一点C 关于x 轴的对称点为D ,若直线AC 的斜率为m ,直线BD 的斜率为n ,则当9mn mn+取到最小值时,双曲线离心率为()A.3B.4C.D.2二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知复数z 满足210z z ++=,则()A.1i 22z =-+ B.1z =C.2z z= D.2320240z z z z ++++= 10.过线段()404x y x +=≤≤上一点P 作圆22:4O x y +=的两条切线,切点分别为,A B ,直线AB 与,x y 轴分别交于点,M N ,则()A.点O 恒在以线段AB 为直径的圆上B.四边形PAOB 面积的最小值为4C.AB 的最小值为D.OM ON +的最小值为411.已知函数())ln1f x x =+,则()A.()f x 在其定义域上是单调递减函数B.()y f x =的图象关于()0,1对称C.()f x 的值域是()0,∞+D.当0x >时,()()f x f x mx --≥恒成立,则m 的最大值为1-三、填空题:本题共3小题,每小题5分,共15分.12.已知随机变量X 服从二项分布B~(n,p),若E (X)=30,D (X)=20,则P=__________.13.已知抛物线22(0)y px p =>的焦点F 为椭圆22143x y +=的右焦点,直线l 过点F 交抛物线于,A B 两点,且8AB =.直线12,l l 分别过点,A B 且均与x 轴平行,在直线12,l l 上分别取点,M N (,M N 均在点,A B 的右侧),ABN ∠和BAM ∠的角平分线相交于点P ,则PAB 的面积为__________.14.已知正方体1111ABCD A B C D -的棱长为,M N 为体对角线1BD 的三等分点,动点P 在三角形1ACB 内,且三角形PMN 的面积263PMN S =△,则点P 的轨迹长度为___________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.如图所示,圆O 的半径为2,直线AM 与圆O 相切于点,4A AM =,圆O 上的点P 从点A 处逆时针转动到最高点B 处,记(],0,πAOP θθ∠=∈.(1)当2π3θ=时,求APM △的面积;(2)试确定θ的值,使得APM △的面积等于AOP 的面积的2倍.16.如图,直三棱柱111ABC A B C -中,D ,E 分别是AB ,1BB 的中点,12AA AC CB AB ===.(1)证明:1//BC 平面1A CD ;(2)求二面角1D A C E --的正弦值.17.盒中有大小颜色相同的6个乒乓球,其中4个未使用过(称之为新球),2个使用过(称之为旧球).每局比赛从盒中随机取2个球作为比赛用球,比赛结束后放回盒中.使用过的球即成为旧球.(1)求一局比赛后盒中恰有3个新球的概率;(2)设两局比赛后盒中新球的个数为X ,求X 的分布列及数学期望.18.已知函数()()21ln ,,2f x x a x a f x =∈'-R 是()f x 的导函数,()e x g x x =.(1)求()f x 的单调区间;(2)若()f x 有唯一零点.①求实数a 的取值范围;②当0a >时,证明:()()4g x f x >'+.19.已知有穷数列12:n A a a a ,,,(3)n ≥中的每一项都是不大于n 的正整数.对于满足1m n ≤≤的整数m ,令集合(){}12k A m k a m k n === ,,,,.记集合()A m 中元素的个数为()s m (约定空集的元素个数为0).(1)若:63253755A ,,,,,,,,求(5)A 及(5)s ;(2)若12111()()()n n s a s a s a +++= ,求证:12,,,n a a a 互不相同;(3)已知12,a a a b ==,若对任意的正整数()i j i j i j n ≠+≤,,都有()i i j A a +∈或()j i j A a +∈,求12n a a a +++ 的值.山东省实验中学2024届高三调研考试数学试题2024.2说明:本试卷满分150分.试题答案请用2B 铅笔和0.5mm 签字笔填涂到答题卡规定位置上,书写在试题上的答案无效.考试时间120分钟.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.设{}{}21,4,2,1,A x B x ==,若B A ⊆,则x =()A.0B.0或2C.0或2- D.2或2-【答案】C 【解析】【分析】根据B A ⊆,可得24x =或22x x =,结合集合元素性质分别求解即可.【详解】由B A ⊆得24x =或22x x =,即0x =或2x =或2x =-,当0x =时,{}{}1,4,0,1,0A B ==,符合题意;当2x =时,{}{}1,4,4,1,4A B ==,不符合元素的互异性,舍去;当2x =-时,{}{}1,4,4,1,4A B =-=,符合题意;综上,0x =或2x =-.故选:C .2.若22nx ⎫⎪⎭展开式中只有第6项的二项式系数最大,则n =()A.9B.10C.11D.12【答案】B 【解析】【分析】利用二项式系数的性质直接求解即可.【详解】因为22nx ⎫+⎪⎭的展开式中只有第6项的二项式系数最大,所以展开式一共有11项,即10n =.故选:B3.已知向量()()1,3,2,2a b ==,则cos ,a b a b +-= ()A.117B.1717C.D.【答案】B 【解析】【分析】根据向量的坐标运算即可求解.【详解】因为()()1,3,2,2a b ==,所以()()3,5,1,1a b a b +=-=-,所以()()·cos ,17a b a b a b a b a b a b+-+-==+-.故选:B.4.等差数列{}n a 的首项为1,公差不为0,若236,,a a a 成等比数列,则{}n a 前6项的和为()A.24-B.3- C.3D.8【答案】A【解析】【分析】设等差数列{}n a 的公差()0d d ≠,由236,,a a a 成等比数列求出d ,代入6S 可得答案.【详解】设等差数列{}n a 的公差()0d d ≠,∵等差数列{}n a 的首项为1,236,,a a a 成等比数列,∴2326a a a =⋅,∴()()()211125+=++a d a d a d ,且11a =,0d ≠,解得2d =-,∴{}n a 前6项的和为61656566122422()⨯⨯=+=⨯+-=-S a d .故选:A.5.要得到函数cos 2y x =的图象,只需将函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图象沿x 轴A.向左平移12π个单位 B.向左平移6π个单位C.向右平移6π个单位 D.向右平移12π个单位【答案】A 【解析】【分析】先用诱导公式把正弦型函数化为余弦型函数,然后根据图象的平移变换的解析式的特征变化,得到答案.【详解】sin 2sin 2cos 2cos[2(326612y x x x x πππππ⎛⎫⎛⎫⎛⎫=+=+-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,因此该函数图象向左平移12π个单位,得到函数cos 2y x =的图象,故本题选A.【点睛】本题考查了已知变化前后的函数解析式,求变换过程的问题,考查了余弦函数图象变换特点.6.在三棱锥-P ABC 中,点M,N 分别在棱PC,PB 上,且13PM PC =,23PN PB =,则三棱锥P AMN -和三棱锥-P ABC 的体积之比为()A.19B.29C.13D.49【答案】B 【解析】【分析】分别过,M C 作,MM PA CC PA ''⊥⊥,垂足分别为,M C ''.过B 作BB '⊥平面PAC ,垂足为B ',连接PB ',过N 作NN PB ''⊥,垂足为N '.先证NN '⊥平面PAC ,则可得到//BB NN '',再证//MM CC ''.由三角形相似得到13MM CC ''=,'2'3NN BB =,再由P AMN N PAMP ABC B PACV V V V ----=即可求出体积比.【详解】如图,分别过,M C 作,MM PA CC PA ''⊥⊥,垂足分别为,M C ''.过B 作BB '⊥平面PAC ,垂足为B ',连接PB ',过N 作NN PB ''⊥,垂足为N '.因为BB '⊥平面PAC ,BB '⊂平面PBB ',所以平面PBB '⊥平面PAC .又因为平面PBB ' 平面PAC PB '=,NN PB ''⊥,NN '⊂平面PBB ',所以NN '⊥平面PAC ,且//BB NN ''.在PCC '△中,因为,MM PA CC PA ''⊥⊥,所以//MM CC '',所以13PM MM PC CC '==',在PBB '△中,因为//BB NN '',所以23PN NN PB BB '==',所以11123231119332PAM P AMN N PAMP ABC B PACPAC PA MM NN S NN V V V V S BB PA CC BB ----⎛⎫'''⋅⋅⋅⋅ ⎪⎝⎭====⎛⎫'''⋅⋅⋅⋅ ⎪⎝⎭.故选:B7.为研究某池塘中水生植物的覆盖水塘面积x (单位:2dm )与水生植物的株数y (单位:株)之间的相关关系,收集了4组数据,用模型e (0)kx y c c =>去拟合x 与y 的关系,设ln ,z y x =与z 的数据如表格所示:得到x 与z 的线性回归方程2ˆˆ 1.z x a=+,则c =()x3467z22.54.57A.-2B.-1C.2e -D.1e -【答案】C 【解析】【分析】根据已知条件,求得5,4x z ==,进而代入回归方程可求得ˆ2a=-,从而得出ˆ 1.22zx =-,联立ln z y =,即可求得本题答案.【详解】由已知可得,346754x +++==,2 2.5 4.5744z +++==,所以,有ˆ4 1.25a =⨯+,解得ˆ2a =-,所以,ˆ 1.22zx =-,由ln z y =,得ln 1.22y x =-,所以, 1.222 1.2e e e x x y --==⋅,则2e c -=.故选:C .8.双曲线2222:1(0,0)x y M a b a b-=>>的左、右顶点分别为,A B ,曲线M 上的一点C 关于x 轴的对称点为D ,若直线AC 的斜率为m ,直线BD 的斜率为n ,则当9mn mn+取到最小值时,双曲线离心率为()A.3B.4C.D.2【答案】D【解析】【分析】由题意9mn mn+利用均值定理可得3mn =,再利用双曲线的几何性质求解即可.【详解】设(,0),(,0),(,),(,)A a B a C x y D x y --,则ACy m k x a ==+,BD y n k x a -==-,所以222y mn x a-=-,将曲线方程22222x a y a b -=代入得22b mn a=-,又由均值定理得996mn mn mn mn +=+≥,当且仅当9mn mn =,即223bmn a==时等号成立,所以离心率2e ==,故选:D.【点睛】方法点睛:求圆锥曲线的离心率(或离心率的取值范围),常见有两种方法:①求出,a c ,代入公式ce a=;②只需要根据一个条件得到关于,,a b c 的齐次式,结合222b a c =-转化为,a c 的齐次式,然后等式(不等式)两边分别除以a 或2a 转化为关于e 的方程(不等式),解方程(不等式)即可得e (e 的取值范围).二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知复数z 满足210z z ++=,则()A.1i 22z =-+ B.1z =C.2z z = D.2320240z z z z ++++= 【答案】BC【解析】【分析】设()i ,z a b a b =+∈R ,代入题干方程求解判断A ,求复数的模判断B ,根据复数乘方运算及共轭复数的定义判断C ,利用复数的周期性求和判断D.【详解】设()i ,z a b a b =+∈R ,由210z z ++=得()()2i i 10a b a b ++++=,即()()2212i 0a b a ab b -++++=,所以221020a b a ab b ⎧-++=⎨+=⎩,解得1232a b ⎧=-⎪⎪⎨⎪=⎪⎩或1232a b ⎧=-⎪⎪⎨⎪=-⎪⎩,所以1i 22z =-+或122z =--,故选项A 错误;由13i 22z =-+,所以1z ==,由122z =--,所以1z ==,故选项B 正确;当13i 22z =-+时,所以2211i 2222z ⎛⎫=-+=-- ⎪ ⎪⎝⎭,13i 22z =--,所以2z z =,当122z =--时,所以221313i i 2222z ⎛⎫=--=-+ ⎪ ⎪⎝⎭,13i 22z =-+,所以2z z =,故选项C 正确;因为321(1)(1)0z z z z -=-++=,所以31z =,所以()()()2320242345620202021202220232024z z z z z z z z z z z z z z z ++++=+++++++++++ ()()()232201722111z z z z z z z z z z =+++++++++++ ()00011=++++-=- ,故选项D 错误.故选:BC10.过线段()404x y x +=≤≤上一点P 作圆22:4O x y +=的两条切线,切点分别为,A B ,直线AB 与,x y 轴分别交于点,M N ,则()A.点O 恒在以线段AB 为直径的圆上B.四边形PAOB 面积的最小值为4C.AB 的最小值为D.OM ON +的最小值为4【答案】BCD 【解析】【分析】设(),4P a a -,则可求AB 的方程为(4)40ax a y +--=.结合,,,O A P B 四点共圆可判断A 的正误,求出OP 的最小值后可判断B 的正误,求出AB 所过的定点后可判断C 的正误,结合AB 的方程可求OM ON +,利用二次函数的性质可求其最小值,故可判断D 的正误.【详解】设(),4P a a -,因为AB 与,x y 轴均相交,故04a <<,连接,OA OB ,设线段:4(04)l x y x +=<<,则,,,O A P B 四点共圆,且此圆以OP 为直径,而以OP 为直径的圆的方程为:()()40x x a y y a -+-+=,整理得到:22(4)0x y ax a y +---=,故AB 的方程为:4(4)0ax a y ---=,整理得到:(4)40ax a y +--=.对于A ,若O 在以线段AB 为直径的圆上,则90AOB ∠=︒,由,,,O A P B 四点共圆可得90APB ∠=︒,而90∠=∠=︒PAO PBO ,2AO BO ==,故四边形OAPB 为正方形,故OP =,但P 为动点且OP 长度变化,故O 不恒在以线段AB 为直径的圆上,故A 错误.对于B ,四边形PAOB 面积为122S OA AP =⨯⨯⨯=而PO ≥=,当且仅当OP ⊥l 即()2,2P 时等号成立,故S 的最小值为4,故B 成立.对于C ,因为AB 的方程为:(4)40ax a y +--=,整理得到:()440a x y y -+-=,令0440x y y -=⎧⎨-=⎩得11x y =⎧⎨=⎩,故AB 过定点()1,1Q ,设O 到AB 的距离为d ,则d OQ ≤=故AB =≥,当且仅当d =OQ AB ⊥时等号成立,故AB 的最小值为,故C 成立.对于D ,由AB 的方程为(4)40ax a y +--=可得44,0,0,4M N a a ⎛⎫⎛⎫⎪ ⎪-⎝⎭⎝⎭,故()24416,04424OM ON a a a a +=+=<<---+,而20(2)44a <--+≤,故4OM ON +≥,当且仅当2a =等号成立,故OM ON +的最小值为4,故D 成立.故选:BCD .11.已知函数())ln1f x x =+,则()A.()f x 在其定义域上是单调递减函数B.()y f x =的图象关于()0,1对称C.()f x 的值域是()0,∞+D.当0x >时,()()f x f x mx --≥恒成立,则m 的最大值为1-【答案】ACD 【解析】【分析】选项A ,先求原函数的导函数,再判断其导函数的符号即可;选项B ,取譬如“点(1,(1))f --和点(1,(1))f ”的特殊值判断即可;选项C ,||x x >=≥,11x +>,进而判断即可;选线D ,先构造函数()()()F x f x f x mx =---,将不等式的恒成立问题转化为函数的最值,即可判断.【详解】已知函数())ln 1f x x =+,||x x >=≥0x ->,故函数()f x 的定义域为R ,对于选项A ,函数()f x 的导函数为:()f x '=,0x ->,得()0f x '<,所以()f x 在其定义域上是单调递减函数,选项A 正确;对于选项B ,取特值:(1)ln f =(1)2)f -=+,且(1)(1)ln 2ln(22)ln(222)1222f f +-++==≠,即函数图象上存在点(1,(1))f --和点(1,(1))f 不关于()0,1对称,选项B 错误;对于选项C 0x ->11x -+>,得())ln1ln10f x x =-+>=,当x →+∞111x -+=+→,当x →-∞1x -+→+∞,同时()f x 在其定义域上是单调递减函数,故()f x 的值域是()0,∞+选项C 正确;对于选项D ,定义()()()F x f x f x mx =---,0x >,则))()ln1ln1F x x x mx =-+-++-,)()ln 1ln1F x x mx ⎛⎫=-++-⎪⎭,)()ln ln1F x x mx ⎛⎫=-+-,故)()lnF x x mx =-+-,其导函数()F x m m'==-,若,()0x ∈+∞,()()f x f x mx --≥恒成立,即函数()0F x ≥恒成立,由于(0)0F =,则(0)0F '≥在()0,x ∈+∞上恒成立,即(0)10F m '=--≥,得1m ≤-,当1m =-时,)()lnG x x x =-++,,()0x ∈+∞()1G x '=+,由于,()0x ∈+∞,则1>1<,()10G x '=+>,所以函数()G x 在区间(0,)+∞上单调递增,且(0)ln100G =-+=,则,()0x ∈+∞时,()0G x >恒成立,同时,()0x ∈+∞,由于1m ≤-,mx x -≥则))()lnln()0F x x mx x x G x =--≥-++=>,显然()0F x >恒成立,,()0x ∈+∞时,()()f x f x mx --≥恒成立,则m 的最大值为1-正确;选项D 正确;故选:ACD.【点睛】关键点点睛:本题D 选项的关键是转化为(0)0F '≥在()0,x ∈+∞上恒成立,从而得到1m ≤-,最后验证得到1m =-时符合题意即可.三、填空题:本题共3小题,每小题5分,共15分.12.已知随机变量X 服从二项分布B~(n,p),若E (X)=30,D (X)=20,则P=__________.【答案】13【解析】【详解】试题分析:直接利用二项分布的期望与方差列出方程求解即可.解:随机变量X 服从二项分布B (n ,p ),若E (X )=30,D (X )=20,可得np=30,npq=20,q=,则p=,故答案为.点评:本题考查离散型随机变量的分布列的期望以及方差的求法,考查计算能力.13.已知抛物线22(0)y px p =>的焦点F 为椭圆22143x y +=的右焦点,直线l 过点F 交抛物线于,A B 两点,且8AB =.直线12,l l 分别过点,A B 且均与x 轴平行,在直线12,l l 上分别取点,M N (,M N 均在点,A B 的右侧),ABN ∠和BAM ∠的角平分线相交于点P ,则PAB 的面积为__________.【答案】【解析】【分析】当直线l 的斜率不存在时,写出直线l 的方程,求出||4AB =,不合题意;当直线l 的斜率存在时,设直线l 的方程为(1)y k x =-,1(A x ,1)y ,2(B x ,2)y ,联立抛物线的方程,由12||8AB x x p =+=+,求出k ,根据锐角三角函数表达边长,再进一步求出PAB 的面积.【详解】由22143x y +=的右焦点为()1,0,所以抛物线的焦点为(1,0)F ,故12p=,则2p =,因此抛物线24y x =,当直线l 的斜率不存在时,直线l 的方程为1x =,代入抛物线的方程,得2y =±,所以(1,2)A ,(1,2)B -,所以||4AB =,不合题意,当直线l 的斜率存在时,设直线l 的方程为(1)y k x =-,1(A x ,1)y ,2(B x ,2)y ,联立2(1)4y k x y x =-⎧⎨=⎩,得2222(24)0k x k x k -++=,所以212224k x x k ++=,所以221212222444||2822p p k k AB x x x x p k k ++=+++=++=+==,所以1k =±,由对称性不妨设1k =,则45AFx ∠=︒,因为ABN ∠和BAM ∠的平分线相交于点P ,//AM BN ,所以PA PB ⊥,45ABN ∠=︒,22.5ABP ∠=︒,所以在Rt ABP 中,sin 22.58sin 22.5AP AB =︒=︒,cos 22.58cos 22.5BP AB =︒=︒,所以18sin 22.58cos 22.52ABP S =⋅︒⋅︒ 32sin 22.58cos 22.516sin 45=︒︒=︒=,故答案为:14.已知正方体1111ABCD A B C D -的棱长为,M N 为体对角线1BD 的三等分点,动点P 在三角形1ACB 内,且三角形PMN 的面积3PMN S =△,则点P 的轨迹长度为___________.【答案】263π【解析】【分析】由题意求出P 到MN 的距离,又易证1BD ⊥面1AB C ,进而得到P 点在1AB C V 所在平面的轨迹是以263为半径的圆,因为1AB C V 3<,所以该圆一部分位于三角形外,作出图形即可求解.【详解】因为正方体的棱长为16BD =,所以123BD MN ==,设P 到MN 的距离为d ,由1||2PMN S d MN ==263d =,11A D ⊥平面11ABB A ,1AB ⊂平面11ABB A ,∴111A D AB ⊥,又11AB A B ⊥,1111A D A B A = ,∴1AB ⊥平面11A D B ,11BD AB ∴⊥,同理可证1BD AC ⊥,又1AB AC A = ,1BD ∴⊥面1AB C ,P ∴点在1AB C V 所在平面的轨迹是以263为半径的圆,1AB C V内切圆的半径为123=,∴该圆一部分位于三角形外,如图有22226(2)()3x +=,解得63x =,∴6HOB π∠=,∴圆在三角形内的圆弧为圆周长的一半,∴1262622l π=⋅⋅,故答案为:263π.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.如图所示,圆O 的半径为2,直线AM 与圆O 相切于点,4A AM =,圆O 上的点P 从点A 处逆时针转动到最高点B 处,记(],0,πAOP θθ∠=∈.(1)当2π3θ=时,求APM △的面积;(2)试确定θ的值,使得APM △的面积等于AOP 的面积的2倍.【答案】(1)6(2)π2θ=【解析】【分析】(1)过点P 作PQ AM ⊥,利用圆的性质求得PQ ,代入面积公式直接求解即可;(2)设AOP 的面积为1,S APM 的面积为2S ,结合三角形面积公式建立方程,利用辅助角公式化简求解即可.【小问1详解】过点P 作PQ AM ⊥交AM 于点Q ,如图:因为圆O 的半径为2,由题意π2π22sin 22cos 22cos 323PQ θθ⎛⎫=+-=-=-= ⎪⎝⎭,又4AM =,所以APM △的面积为14362⨯⨯=.【小问2详解】连接AP ,设AOP 的面积为1,S APM 的面积为2S ,又1122sin 2sin 2S θθ=⨯⨯⨯=,()()211421cos 41cos 22S AM PQ θθ=⋅=⨯⨯⨯-=-,由题意212S S =,所以()41cos 4sin θθ-=,即sin cos 1θθ+=,所以π2sin 42θ⎛⎫+= ⎪⎝⎭,因为()0,πθ∈,所以ππ5π,444θ⎛⎫+∈ ⎪⎝⎭,所以π3π44θ+=,所以π2θ=,所以当π2θ=时,使得APM △的面积等于AOP 的面积的2倍.16.如图,直三棱柱111ABC A B C -中,D ,E 分别是AB ,1BB 的中点,122AA AC CB AB ===.(1)证明:1//BC 平面1A CD ;(2)求二面角1D A C E --的正弦值.【答案】(Ⅰ)见解析(Ⅱ)63【解析】【分析】(Ⅰ)利用三角形中位线定理可得1//DF BC ,由线面平行的判定定理可得结果;(Ⅱ)由122AA AC CB AB ===,可设:AB=2a ,可得AC BC ⊥,以点C 为坐标原点,分别以直线1,,CA CB CC 为x 轴、y 轴、z 轴,建立空间直角坐标系如图,利用向量垂直数量积为零列方程分别求出平面1A CD 的法向量、平面1A CE 的一个法向量,再由空间向量夹角余弦公式可得结果.【详解】(Ⅰ)如图,连结1AC ,交1AC 于点F ,连结DF ,因为D 是AB 的中点,所以在1ABC 中,DF 是中位线,所以1DF / / BC ,因为DF ⊂平面1A CD ,1BC ⊄平面1A CD ,所以1//BC 平面1A CD ;(Ⅱ)因为2AC CB AB ==,所以90ACB ︒∠=,即ACBC ⊥,则以C 为坐标原点,分别以1,,CA CB CC为,,x y z 轴的正方向,建立如图所示的空间直角坐标系,设1AA =AC=CB=2,则1(0,0,0),(1,1,0),(0,2,1),(2,0,2)C D E A ,则1(1,1,0),(0,2,1),(2,0,2)CD CE CA ===,设()111,,m x y z =r是平面1DA C 的一个法向量,则,即11110220x y x z +=⎧⎨+=⎩,取11x =,则111,1=-=-y z ,则(1,1,1)n =--同理可得平面1EA C 的一个法向量,则(2,1,2)n =-,所以,3cos ,3m n 〈〉=,所以sin ,3m n 〈〉=,即二面角D AC E --的正弦值为.63【点睛】本题主要考查线面平行的判定定理、利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.17.盒中有大小颜色相同的6个乒乓球,其中4个未使用过(称之为新球),2个使用过(称之为旧球).每局比赛从盒中随机取2个球作为比赛用球,比赛结束后放回盒中.使用过的球即成为旧球.(1)求一局比赛后盒中恰有3个新球的概率;(2)设两局比赛后盒中新球的个数为X ,求X 的分布列及数学期望.【答案】(1)815(2)分布列见解析,169【解析】【分析】(1)根据超几何分布概率公式求解即可;(2)根据超几何分布概率公式求得分布列,进而求得数学期望即可.【小问1详解】由题意可知当比赛使用1个新球,1个旧球时,盒中恰有3个新球,使用一局比赛后盒中恰有3个新球的概率112642C C 8C 15P ==.【小问2详解】由题意可知X 的可能取值为0,1,2,3,4,()22422266C C 60C C 225P X ==⋅=,()22111134424222226666C C C C C C 721+C C C C 225P X ==⋅⋅=,()1122112233444224222222666666C C C C C C C C 1142++C C C C C C 225P X ==⋅⋅⋅=,()22111132424222226666C C C C C C 323+C C C C 225P X ==⋅⋅=,()22222266C C 14C C 225P X ==⋅=,所以X 的分布列为X01234P622572225114225322251225()67211432116012342252252252252259E X =⨯+⨯+⨯+⨯+⨯=.18.已知函数()()21ln ,,2f x x a x a f x =∈'-R 是()f x 的导函数,()e xg x x =.(1)求()f x 的单调区间;(2)若()f x 有唯一零点.①求实数a 的取值范围;②当0a >时,证明:()()4g x f x >'+.【答案】(1)答案见解析(2)①(){},0e -∞ ;②证明见解析【解析】【分析】(1)对()f x 求导得到()2x a f x x='-,根据导数与函数单调性间的关系,对a 分类讨论,即可得出结果;(2)①法一:直接对a 进行分类讨论,利用(1)的结果,即可得出结果;法二:分离常量得到21ln 2x a x=,构造函数()2ln xx x ϕ=,将问题转化成函数图象交点个数来解决问题;②构造函数()1e 2e (0)2xh x x x x ⎛⎫=--> ⎪⎝⎭,通过求导,利用导数与函数单调性间的关系,得到()h x 的最小值,从而得出()1e 2e 2xg x x x ⎛⎫=≥-⎪⎝⎭,从而将问题转化成证明()()22e 1e 4e 0x x --++>,即可证明结果.【小问1详解】()f x 的定义域为()0,∞+,()2a x af x x x x='-=-,当0a ≤时,()0f x '>恒成立,此时()f x 的单调递增区间是()0,∞+,无单调递减区间,当0a >时,令()0f x '>得x >()0f x '<得0x <<;此时()f x 单调递减区间为(;单调递增区间为)∞+,综上,当0a ≤时,()f x 的单调递增区间是()0,∞+,无单调递减区间,当0a >时,()f x 单调递减区间为(,单调递增区间为)∞+.【小问2详解】①法一;当0a =时,()f x 没有零点,不符合题意;当a<0时,由(1)知函数()f x 在()0,∞+单调递增,因为()()2211ln 122f x x a x x a x =-<--,取0m a =>,则()21((1)(3)02f m a a a a a <+-+-=++<,又()1102f =>,故存在唯一()0,1x m ∈,使得()00f x =,符合题意;当0a >时,由(1)可知,()f x 有唯一零点只需0f =,即ln 022a aa -=,解得e a =,综上,a 的取值范围为(){},0e ∞-⋃.法二:当0a =时,()f x 没有零点,不符合题意;由()0f x =,得到21ln 2x a x =,令()2ln x x x ϕ=,则()312ln xx x ϕ-'=,当(x ∈时,()0x ϕ'>,则()x ϕ在区间(单调递增,当)x ∞∈+时,()0x ϕ'<,则()x ϕ在区间)∞+单调递减,又lim ()0x x ϕ→+∞=,()0lim x x ϕ∞+→=-,所以102a <或1122ea ϕ==,即a<0或e a =,综上,a 的取值范围为(){},0e ∞-⋃.②由①得出e a =,令()1e 2e (0)2xh x x x x ⎛⎫=--> ⎪⎝⎭,则()()1e 2e xh x x '=+-,令()()1e 2e xg x x =+-,则()()2e 0xg x x =+>'恒成立,所以()h x '单调递增,又()10h '=,故当()0,1x ∈时,()0h x '<,则()h x 在区间()0,1上单调递减,当()1,x ∞∈+时,()0h x '>,则()h x 在区间()1,∞+上单调递增;故()()10h x h ≥=,所以()1e 2e 2xg x x x ⎛⎫=≥-⎪⎝⎭,要证()()4g x f x >'+,只需证明()1e2e 442x f x x x⎛⎫->+=-⎪'+ ⎝⎭,即证()()22e 1e 4e 0x x --++>,由22229595Δ12e 167e 12e e 16e e 12e 16e 2222⎛⎫=+-=-+-=-+- ⎪⎝⎭95e 12 2.7167.2022⎛⎫<-⨯+-⨯< ⎪⎝⎭,所以()()22e 1e 4e 0x x --++>成立,故不等式得证.【点睛】关键点点晴:本题的关键在于第(2)问中的②,构造函数()1e 2e (0)2x h x x x x ⎛⎫=--> ⎪⎝⎭,通过求导,利用导数与函数单调性间的关系,得到()h x 的最小值,从而得出()1e 2e 2xg x x x ⎛⎫=≥-⎪⎝⎭,通过放缩,将问题转化成证明()()22e 1e 4e 0x x --++>,从而解决问题.19.已知有穷数列12:n A a a a ,,,(3)n ≥中的每一项都是不大于n 的正整数.对于满足1m n ≤≤的整数m ,令集合(){}12k A m k a m k n === ,,,,.记集合()A m 中元素的个数为()s m (约定空集的元素个数为0).(1)若:63253755A ,,,,,,,,求(5)A 及(5)s ;(2)若12111()()()n n s a s a s a +++= ,求证:12,,,n a a a 互不相同;(3)已知12,a a a b ==,若对任意的正整数()i j i j i j n ≠+≤,,都有()i i j A a +∈或()j i j A a +∈,求12n a a a +++ 的值.【答案】(1)(5){478}A =,,,(5)=3s .(2)证明见解析(3)答案见解析【解析】【分析】(1)观察数列,结合题意得到(5)A 及(5)s ;(2)先得到11()i s a ≤,故12111()()()n n s a s a s a +++≤ ,再由12111()()()n n s a s a s a +++= 得到()1i s a =,从而证明出结论;(3)由题意得i j i a a +=或i j j a a +=,令1j =,得到32a a =或31a a =,当a b =时得到12n a a a na +++= ,当a b ¹时,考虑3a a =或3a b =两种情况,求出答案.【小问1详解】因为4785a a a ===,所以{}(5)4,7,8A =,则(5)=3s ;【小问2详解】依题意()1,12i s a i n ≥=,,, ,则有11()i s a ≤,因此12111()()()n n s a s a s a +++≤ ,又因为12111()()()n n s a s a s a +++= ,所以()1i s a =所以12,,,n a a a 互不相同.【小问3详解】依题意12,.a a ab ==由()i i j A a +∈或()j i j A a +∈,知i j i a a +=或i j j a a +=.令1j =,可得1i i a a +=或11i a a +=,对于2,3,...1i n =-成立,故32a a =或31a a =.①当a b =时,34n a a a a ==== ,所以12n a a a na +++= .②当a b ¹时,3a a =或3a b =.当3a a =时,由43a a =或41a a =,有4a a =,同理56n a a a a ==== ,所以12(1)n a a a n a b +++=-+ .当3a b =时,此时有23a a b ==,令13i j ==,,可得4()A a ∈或4()A b ∈,即4a a =或4a b =.令14i j ==,,可得5()A a ∈或5()A b ∈.令23i j ==,,可得5()A b ∈.所以5a b =.若4a a =,则令14i j ==,,可得5a a =,与5a b =矛盾.所以有4a b =.不妨设23(5)k a a a b k ====≥ ,令1(2,3,,1)i t j k t t k ==+-=-, ,可得1()k A b +∈,因此1k a b +=.令1,i j k ==,则1k a a +=或1k a b +=.故1k a b +=.所以12(1)n a a a n b a +++=-+ .综上,a b =时,12n a a a na +++= .3a a b =≠时,12(1)n a a a n a b +++=-+ .3a b a =≠时,12(1)n a a a n b a +++=-+ .【点睛】数列新定义问题的方法和技巧:(1)可通过举例子的方式,将抽象的定义转化为具体的简单的应用,从而加深对信息的理解;(2)可用自己的语言转述新信息所表达的内容,如果能清晰描述,那么说明对此信息理解的较为透彻;(3)发现新信息与所学知识的联系,并从描述中体会信息的本质特征与规律;(4)如果新信息是课本知识的推广,则要关注此信息与课本中概念的不同之处,以及什么情况下可以使用书上的概念,要将“新”性质有机地应用到“旧”性质上,创造性的解决问题.。

2016-2017学年山东省潍坊实验中学高三(下)第一次过关数学试卷(理科)一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选顶中,只有一项是符合题目要求的.1.已知i是虚数单位,若复数z满足(1+i)z=2i,则z的虚部是()A.1 B.﹣1 C.﹣i D.i2.已知集合A={3,a2},B={2,1﹣a,b},且A∩B={1},则A∪B=()A.{0,1,3}B.{1,2,3}C.{1,2,4}D.{0,1,2,3}3.下列说法正确的是()A.命题“2≥1”是假命题B.命题“∀x∈R,x2+1>0”的否定是:<0C.命题“若2a>2b,则a>b”的否命题是“若2a>2b,则a≤b”D.“x>1”是“x2+x+2>0”充分不必要条件4.设函数f(x)=x•e cosx(x∈[﹣π,π])的图象大致是()A.B.C.D.5.某兴趣小组有男生20人,女生10人,从中抽取一个容量为5的样本,恰好抽到2名男生和3名女生,则①该抽样可能是系统抽样;②该抽样可能是随机抽样:③该抽样一定不是分层抽样;④本次抽样中每个人被抽到的概率都是.其中说法正确的为()A.①②③B.②③C.②③④D.③④6.设D,E,F分别△ABC的三边AB,BC,CA的中点,则=()A.B. C.D.7.一个圆柱的正视图是面积为6的矩形,它的侧面积为()A.8πB.6πC.4πD.3π8.若tanα=3,则=()A.B.C.D.9.已知过双曲线﹣=1(a>0,b>0)的左焦点F(﹣c,0)和虚轴端点E 的直线交双曲线的右支于点P,若E为线段FP的中点,则该双曲线的离心率为()A.B.C.D. +110.函数的部分图象如图所示,其中,给出下列结论:①最小正周期为π;②f(0)=1;③函数是偶函数;④;⑤.其中正确结论的个数是()A.5 B.4 C.3 D.2二、填空题:本大题共5小题,每小题5分,共25分,把答案填在题中横线上.11.若函数f(x)=2x﹣3,且f(m+1)=5,则m=.12.执行如图所示的程序框图,则输出k的值为.13.如果实数x,y满足不等式组则目标函数z=3x﹣2y的最大值是.14.若2是函数f(x)=x3﹣ax(a∈R)的零点,则在(0,a)内任取一点x0,使lnx0<0的概率是.15.直线ax+2by+2=0与圆x2+y2=2相切,切点在第一象限内,则的最小值为.三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.16.设函数.(I)求f(x)的最小正周期及值域;(II)已知△ABC中,角A,B,C的对边分别为a,b,c,若,求△ABC的面积.17.已知等差数列{a n}中,S n为其前n项和,a2+a6=6,S3=5.(I)求数列{a n}的通项公式;(II)令,若T n<m对一切n∈N*都成立,求m的最小值.18.某高中学校为展示学生的青春风采,举办了校园歌手大赛,该大赛分为预赛和决赛两个阶段,参加决赛的学生按照抽签方式决定出场顺序,通过预赛,选拔出甲、乙等5名学生参加决赛.(I)求决赛中学生甲、乙恰好排在前两位的概率;(Ⅱ)若决赛中学生甲和学生乙之间间隔的人数记为X,求X的分布列及数学期望EX.19.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,PA=PD=2,BC=AD=1,CD=.(1)求证:平面PQB⊥平面PAD;(2)在棱PC上是否存在一点M,使二面角M﹣BQ﹣C为30°,若存在,确定M 的位置,若不存在,请说明理由.20.已知椭圆,其短轴的一个端点与两个焦点构成面积为的正三角形,过椭圆C的右焦点作斜率为k(k≠0)的直线l与椭圆C相交于A、B两点,线段AB的中点为P.(I)求椭圆C的标准方程;(II)过点P垂直于AB的直线与x轴交于点D,试求的取值范围.21.设函数f(x)=x2﹣aln(x+2),且f(x)存在两个极值点x1,x2,其中x1<x2.(I)求实数a的取值范围;(II)证明不等式:.2016-2017学年山东省潍坊实验中学高三(下)第一次过关数学试卷(理科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选顶中,只有一项是符合题目要求的.1.已知i是虚数单位,若复数z满足(1+i)z=2i,则z的虚部是()A.1 B.﹣1 C.﹣i D.i【考点】复数代数形式的乘除运算.【分析】由(1+i)z=2i,得,然后利用复数代数形式的乘除运算化简得答案.【解答】解:由(1+i)z=2i,得=,则z的虚部是:1.故选:A.2.已知集合A={3,a2},B={2,1﹣a,b},且A∩B={1},则A∪B=()A.{0,1,3}B.{1,2,3}C.{1,2,4}D.{0,1,2,3}【考点】并集及其运算.【分析】由A与B交集的元素为1,得到1属于A且属于B,得到a2=1,求出a 的值,进而求出b的值,确定出A与B,找出既属于A又属于B的元素,即可确定出两集合的并集.【解答】解:∵A={3,a2},集合B={2,1﹣a,b},且A∩B={1},∴a2=1,解得:a=1或a=﹣1,当a=1时,1﹣a=1﹣1=0,此时b=1,当a=﹣1时,1﹣a=1﹣(﹣1)=2,不合题意,舍去;∴A={3,1},集合B={0,1,2},则A∪B={0,1,2,3}.故选D3.下列说法正确的是()A.命题“2≥1”是假命题B.命题“∀x∈R,x2+1>0”的否定是:<0C.命题“若2a>2b,则a>b”的否命题是“若2a>2b,则a≤b”D.“x>1”是“x2+x+2>0”充分不必要条件【考点】四种命题.【分析】利用命题的定义以及四个命题之间的关系分别对选项分析选择.【解答】解:A,“2≥1”不是命题;故A错误;B.命题“∀x∈R,x2+1>0”的否定是:≥0;故B错误;C.命题“若2a>2b,则a>b”的否命题是“若2a≤2b,则a≤b”;故C错误;D.“x>1”能够推出“x2+x+2>0”;但是“x2+x+2>0”⇒x∈R,不一定⇒“x>1”;所以“x>1”是充分不必要条件.故选:D.4.设函数f(x)=x•e cosx(x∈[﹣π,π])的图象大致是()A.B.C.D.【考点】函数的图象.【分析】判断函数的奇偶性,然后利用特殊点判断选项即可.【解答】解:函数f(x)=x•e cosx(x∈[﹣π,π])f(﹣x)=﹣x•e cos(﹣x)=﹣x•e cosx=﹣f(x),函数是奇函数,排除B、D选项.当x=π时f(π)=π•e cosπ=.即()在函数的图象上,所以A正确,C不正确.故选:A.5.某兴趣小组有男生20人,女生10人,从中抽取一个容量为5的样本,恰好抽到2名男生和3名女生,则①该抽样可能是系统抽样;②该抽样可能是随机抽样:③该抽样一定不是分层抽样;④本次抽样中每个人被抽到的概率都是.其中说法正确的为()A.①②③B.②③C.②③④D.③④【考点】收集数据的方法.【分析】①该抽样可以是系统抽样;②因为总体个数不多,容易对每个个体进行编号,因此该抽样可能是简单的随机抽样;③若总体由差异明显的几部分组成时,经常采用分层抽样的方法进行抽样,且分层抽样的比例相同,该抽样不可能是分层抽样;④分别求出男生和女生的概率,故可判断出真假【解答】解:①总体容量为30,样本容量为5,第一步对30个个体进行编号,如男生1~20,女生21~30;第二步确定分段间隔k==6;第三步在第一段用简单随机抽样确定第一个个体编号l(l≤10);第四步将编号为l+6k(0≤k≤4)依次抽取,即可获得整个样本.故该抽样可以是系统抽样.因此①正确.②因为总体个数不多,可以对每个个体进行编号,因此该抽样可能是简单的随机抽样,故②正确;③若总体由差异明显的几部分组成时,经常采用分层抽样的方法进行抽样,且分层抽样的比例相同,但兴趣小组有男生20人,女生10人,抽取2男三女,抽的比例不同,故③正确;④该抽样男生被抽到的概率=;女生被抽到的概率=,故前者小于后者.因此④不正确.故选:A.6.设D,E,F分别△ABC的三边AB,BC,CA的中点,则=()A.B. C.D.【考点】向量的三角形法则.【分析】利用向量平行四边形法则即可得出.【解答】解:∵=,,∴=﹣==.故选:C.7.一个圆柱的正视图是面积为6的矩形,它的侧面积为()A.8πB.6πC.4πD.3π【考点】旋转体(圆柱、圆锥、圆台);简单空间图形的三视图.【分析】设圆柱的高为h,由题意知,圆柱体的底面圆的直径,圆柱的侧面积为S=πDh.【解答】解:设圆柱的高为h,则∵圆柱的正视图是面积为6的矩形,∴圆柱体的底面圆的直径为,则此圆柱的侧面积为S=π••h=6π.故选:B.8.若tanα=3,则=()A.B.C.D.【考点】三角函数的化简求值.【分析】利用诱导公式、倍角公式、“弦化切”即可得出.【解答】解:=﹣==﹣sin2α=﹣=﹣=﹣=﹣,故选:A.9.已知过双曲线﹣=1(a>0,b>0)的左焦点F(﹣c,0)和虚轴端点E 的直线交双曲线的右支于点P,若E为线段FP的中点,则该双曲线的离心率为()A.B.C.D. +1【考点】双曲线的简单性质.【分析】由题意,P(c,2b),代入双曲线﹣=1,可得=1,即可求出该双曲线的离心率.【解答】解:由题意,P(c,2b),代入双曲线﹣=1,可得=1,∴e=,故选B.10.函数的部分图象如图所示,其中,给出下列结论:①最小正周期为π;②f(0)=1;③函数是偶函数;④;⑤.其中正确结论的个数是( )A .5B .4C .3D .2【考点】由y=Asin (ωx +φ)的部分图象确定其解析式;正弦函数的图象.【分析】由函数的最值求出A ,由周期求出ω,由图象经过定点(,0),求出φ的值,从而求得函数的解析式,利用三角函数的图象和性质逐一分析各个选项即可得解.【解答】解:由图象可知,A=2, T=﹣,则T=π.故①正确,又由于ω=,则ω=2,故f (x )=2sin (2x +φ).由题中图象可知,f ()=2sin (2×+φ)=0,则+φ=kπ,k ∈z ,即 φ=kπ﹣,k ∈z .又因为|φ|<,则 φ=,所以函数解析式为f (x )=2sin (2x +),对于②:由于f (0)=2sin =,故②错误,对于③: =2sin [2(x ﹣)+]=2sin2x ,为奇函数,故③错误,对于④:由于:f ()=2sin (2×+)=2sin =2sin =2cos,f ()=2sin (2×+)=2sin =2cos,又由于:>>>0,所以:cos<cos,可得正确,对于⑤:用特值法,当x=时,f()+f(﹣)=0+f(π)=0+2sin=,故错误.故选:D.二、填空题:本大题共5小题,每小题5分,共25分,把答案填在题中横线上.11.若函数f(x)=2x﹣3,且f(m+1)=5,则m=2.【考点】函数的值.【分析】由题意得2m+1﹣3=5,由此能求出m的值.【解答】解:∵f(x)=2x﹣3,且f(m+1)=5,∴2m+1﹣3=5,解得m=2.故答案为:2.12.执行如图所示的程序框图,则输出k的值为7.【考点】程序框图.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是输出输出不满足条件S=0+2+4+…<100时,k+1的值.【解答】解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是:输出不满足条件S=0+2+4+…<100时,k+1的值.由于2+4+…+25<100,k=6;满足判断框的条件,继续运行,2+4+…+26>100,k=7,不满足判断框的条件,退出循环.故最后输出k的值为7.故713.如果实数x,y满足不等式组则目标函数z=3x﹣2y的最大值是1.【考点】简单线性规划.【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.【解答】解:由约束条件作出可行域如图,联立,解得A(3,4).化目标函数z=3x﹣2y为y=,由图可知,当直线y=过A时,直线在y轴上的截距最小,z有最大值为1.故答案为:1.14.若2是函数f(x)=x3﹣ax(a∈R)的零点,则在(0,a)内任取一点x0,使lnx0<0的概率是.【考点】几何概型.【分析】首先由零点求出a,然后求出满足lnx0<0的范围,利用几何概型的公式得到所求.【解答】解:由题意,2是函数f(x)=x3﹣ax(a∈R)的零点,则a=4,在(0,4)内任取一点x0,使lnx0<0的x0∈(0,1),由几何概型的公式得到;故答案为:15.直线ax+2by+2=0与圆x2+y2=2相切,切点在第一象限内,则的最小值为.【考点】直线与圆的位置关系.【分析】由题意可得a>0,b>0 且即=.故有a2+4b2=2,再利用基本不等式求出的最小值.【解答】解:若直线ax+2by+2=0与圆x2+y2=2相切于第一象限,则a>0,b>0 且圆心到直线的距离等于半径,即=.故有a2+4b2=2,=()(a2+4b2)=(5++)≥(5+4)=,当且仅当a=2b时,等号成立,即的最小值为,故答案为.三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.16.设函数.(I)求f(x)的最小正周期及值域;(II)已知△ABC中,角A,B,C的对边分别为a,b,c,若,求△ABC的面积.【考点】余弦定理;三角函数中的恒等变换应用.【分析】(Ⅰ)由诱导公式、二倍角公式及变形、两角和的正弦公式化简解析式,由三角函数的周期公式求出f(x)的最小正周期,由条件和正弦函数的值域求出f(x)的值域;(Ⅱ)由(I)化简f(A)=1,由A的范围和特殊角的三角函数值求出A,由余弦定理列出方程化简后,把数据代入求出bc的值,由三角形的面积公式求出△ABC的面积.【解答】解:(Ⅰ)﹣﹣﹣﹣﹣﹣﹣﹣1分)=,﹣﹣﹣﹣所以f(x)的最小正周期T=,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∵x∈R,∴,则,∴函数f(x)的值域为.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(Ⅱ)由(I)得,则,由0<A<π得,∴﹣﹣﹣﹣﹣﹣由余弦定理得,=(b+c)2﹣3bc,又a=,b+c=3,解得bc=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣所以△ABC的面积S===﹣﹣﹣﹣﹣﹣﹣17.已知等差数列{a n}中,S n为其前n项和,a2+a6=6,S3=5.(I)求数列{a n}的通项公式;(II)令,若T n<m对一切n∈N*都成立,求m的最小值.【考点】数列与不等式的综合;等差数列的通项公式.【分析】(Ⅰ)设等差数列{a n}的公差为d,根据题意可得,解得即可,(Ⅱ)根据裂项求和即可得到S n=b1+b2+…+b n=(1﹣),即可求出m的值.【解答】解:(Ⅰ)设等差数列{a n}的公差为d,由a2+a6=6,S3=5得,解得a1=1,d=,∴a n=n+.(Ⅱ)当n≥2时,b n===(﹣)当n=1时,上式同样成立,∴S n=b1+b2+…+b n=(1﹣+﹣+…+﹣)=(1﹣),又(1﹣)随n递增,且(1﹣)<•1≤m,又m∈N*,∴m≥5,∴m的最小值为518.某高中学校为展示学生的青春风采,举办了校园歌手大赛,该大赛分为预赛和决赛两个阶段,参加决赛的学生按照抽签方式决定出场顺序,通过预赛,选拔出甲、乙等5名学生参加决赛.(I)求决赛中学生甲、乙恰好排在前两位的概率;(Ⅱ)若决赛中学生甲和学生乙之间间隔的人数记为X,求X的分布列及数学期望EX.【考点】离散型随机变量的期望与方差;离散型随机变量及其分布列.【分析】(Ⅰ)设“学生甲、乙恰好排在前两位”为事件A,先求出基本事件总数n=,再求出决赛中学生甲、乙恰好排在前两位包含听基本事件个数,由此能求出决赛中学生甲、乙恰好排在前两位的概率.(Ⅱ)随机变量X的可能的值为0,1,2,3.分别求出相应的概率,由此能求出随机变量X的分布列及数学期望EX.【解答】解:(Ⅰ)设“学生甲、乙恰好排在前两位”为事件A,则.(Ⅱ)随机变量X的可能的值为0,1,2,3.,,,.随机变量X的分布列为∴.19.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,PA=PD=2,BC=AD=1,CD=.(1)求证:平面PQB⊥平面PAD;(2)在棱PC上是否存在一点M,使二面角M﹣BQ﹣C为30°,若存在,确定M 的位置,若不存在,请说明理由.【考点】用空间向量求平面间的夹角;平面与平面垂直的判定.【分析】(1)通过四边形BCDQ为平行四边形、∠AQB=90°,及线面垂直、面面垂直的判定定理即得结论;(2)以Q为坐标原点,以QA、QB、QP分别为x、y、z轴建立空间直角坐标系Q﹣xyz,通过平面BQC的一个法向量与平面MBQ的一个法向量的夹角的余弦值为,计算即得结论.【解答】(1)证明:∵AD∥BC,BC=AD,Q为AD的中点,∴BC∥DQ且BC=DQ,∴四边形BCDQ为平行四边形,∴CD∥BQ,∵∠ADC=90°,∴∠AQB=90°,即QB⊥AD,∵PA=PD,∴PQ⊥AD,∵PQ∩BQ=Q,∴AD⊥平面PBQ,∵AD⊂平面PAD,∴平面PQB⊥平面PAD;(2)结论:当M是棱PC上靠近点C的四等分点时有二面角M﹣BQ﹣C为30°.理由如下:∵PA=PD,Q为AD的中点,∴PQ⊥AD,∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PQ⊥平面ABCD.以Q为坐标原点,以QA、QB、QP分别为x、y、z轴建立空间直角坐标系Q﹣xyz 如图,∴Q(0,0,0),P(0,0,),B(0,,0),C(﹣1,,0),则平面BQC的一个法向量为=(0,0,1),设满足条件的点M(x,y,z)存在,则=(x,y,z﹣),=(﹣1﹣x,﹣y,﹣z),令=t,其中t>0,∴,∴,在平面MBQ中,=(0,,0),=(﹣,,),∴平面MBQ的一个法向量为=(,0,t),∵二面角M﹣BQ﹣C为30°,∴cos30°=||==,解得t=3,∴满足条件的点M存在,M是棱PC的靠近点C的四等分点.20.已知椭圆,其短轴的一个端点与两个焦点构成面积为的正三角形,过椭圆C的右焦点作斜率为k(k≠0)的直线l与椭圆C相交于A、B两点,线段AB的中点为P.(I)求椭圆C的标准方程;(II)过点P垂直于AB的直线与x轴交于点D,试求的取值范围.【考点】椭圆的简单性质.【分析】(I)由面积为的正三角形的边长为2,即可求得a和c的值,b2=a2﹣c2,即可求得椭圆C的标准方程;(II)将直线方程,代入椭圆方程,由韦达定理及中点坐标公式,求得P点坐标,求得直线PD的方程及D点坐标,求得丨PD丨及丨AB丨,则,由k的取值范围,即可求得的取值范围.【解答】解:(Ⅰ)设右焦点的坐标为(c,0),易知面积为的正三角形的边长为2,依题意知,,∴b2=a2﹣c2=3,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣所以,椭圆C的方程为.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(Ⅱ)设过椭圆C的右焦点的直线l的方程为y=k(x﹣1),将其代入中得,(3+4k2)x2﹣8k2x+4k2﹣12=0,﹣﹣﹣﹣﹣﹣﹣其中,△=144(k2+1),设A(x1,y1),B(x2,y2),则,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∴,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣因为P为线段AB的中点,所以,点P的坐标为.故点P的坐标为,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣又直线PD的斜率为,直线PD 的方程为,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣令y=0得,,则点D 的坐标为,所以,,﹣﹣﹣﹣﹣﹣﹣又=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣所以,,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣又∵k 2+1>1,∴,∴.所以,的取值范围是.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣21.设函数f (x )=x 2﹣aln (x +2),且f (x )存在两个极值点x 1,x 2,其中x 1<x 2.(I )求实数a 的取值范围;(II )证明不等式:.【考点】利用导数研究函数的极值;利用导数研究函数的单调性.【分析】(I )求导,由题意可知:2x 2+4x ﹣a=0在(﹣2,+∞)内有两个不相等实根,构造辅助函数,利用函数的性质,即可求得实数a 的取值范围;(II)由(I)可知,利用韦达定理,则,构造辅助函数.利用导数求得函数的单调区间,则F(x)<F(1)=﹣1,即.【解答】解:(Ⅰ)由题意,,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∵函数f(x)存在两个极值点x1,x2,且x1<x2,∴关于x的方程,即2x2+4x﹣a=0在(﹣2,+∞)内有两个不相等实根.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣令φ(x)=2x2+4x﹣a,则﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣解得﹣2<a<0.所以,实数a的取值范围(﹣2,0).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(Ⅱ)证明:由(Ⅰ)知∴,﹣﹣﹣﹣﹣﹣﹣﹣﹣令﹣x2=x,则0<x<1,且,令,则﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∴,∵0<x<1,∴F''(x)<0即F'(x)在(0,1)上是减函数,∴F'(x)>F'(1)=1>0,∴F(x)在(0,1)上是增函数,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∴F(x)<F(1)=﹣1,即,所以,.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣2017年3月23日。

命题角度5.2:直线与椭圆位置关系1.已知椭圆的两个焦点为,,且经过点.(1)求椭圆的方程;(2)过的直线与椭圆交于两点(点位于轴上方),若,且,求直线的斜率的取值范围.【答案】(1);(2).【解析】试题分析:(1)由题意可得,,,则椭圆方程为.(2)联立直线与椭圆的方程,结合韦达定理得到关于实数k 的不等式,求解不等式可得直线的斜率的取值范围是k=.2.已知椭圆C 的中心在原点,焦点在x 轴上,离心率e <.以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为 (Ⅰ)求椭圆C 的方程;(Ⅱ)若点()00,P x y 为椭圆C 上一点,直线l 的方程为0034120x x y y +-=,求证:直线l 与椭圆C 有且只有一个交点.【来源】【全国市级联考】广西桂林,百色,梧州,北海,崇左五市2017届高三5月联合模拟理科数学试题【答案】(I )22143x y +=;(II )详见解析. 【解析】试题分析:(1)利用题意求得b = 1c =,椭圆C 的方程为22143x y +=. (2)首先讨论当00y =的情况,否则联立直线与椭圆的方程,结合直线的特点整理可得直线l 与椭圆C 有且只有一个交点.(Ⅱ)当00y =时,由2200143x y +=,可得02x =±, 当02x =, 00y =时,直线l 的方程为2x =,直线l 与曲线C 有且只有一个交点()2,0. 当02x =-, 00y =时,直线l 的方程为2x =-,直线l 与曲线C 有且只有一个交点()2,0-.当00y ≠时,直线l 的方程为001234x xy y -=,联立方程组0022123,4{ 1.43x xy y x y -=+=消去y ,得()22220000432448160y x x x x y +-+-=.①由点()00,P x y 为曲线C 上一点,得2200143x y +=,可得22004312y x +=. 于是方程①可以化简为220020x x x x -+=,解得0x x =,将0x x =代入方程001234x xy y -=可得0y y =,故直线l 与曲线C 有且有一个交点()00,P x y ,综上,直线l 与曲线C 有且只有一个交点,且交点为()00,P x y .3.(0a b >>)的左、右焦点分别为()11,0F -, ()21,0F ,点在椭圆C 上. (1)求椭圆C 的标准方程;(2)是否存在斜率为2的直线l ,使得当直线l 与椭圆C 有两个不同交点,M N 时,能在直线上找到一点P ,在椭圆C 上找到一点Q ,满足PM NQ =?若存在,求出直线l 的方程;若不存在,说明理由.【来源】山西省太原市第五中学2017届高三第二次模拟考试(5月) 数学(理)试题【答案】(1(2)不存在,理由见解析. 【解析】试题分析:(1)由焦点坐标可得1c =,再根据222a b c +=及点C 上,可得222,1a b ==,进而可得椭圆的方程;(2)设直线l 的方程为2y x t =+,与椭圆方程联立可得2298220x tx t ++-=,与判别式为正可得33t -<<,再根据平行四边形性质及韦达定理可得点Q 的纵坐标范围是,可判定点Q 不在椭圆上,所以这样的直线l 不存在. 试题解析:(1)设椭圆C 的焦距为2c ,则1c =,2,2A ⎛ ⎝解得22a = 故椭圆C 的方程为由PM NQ=知四边形PMQN 为平行四边形,而D 为线段MN 的中点,因此, D 也是线段PQ 的中点,因此点Q 不在椭圆上.所以这样的直线l 不存在【方法点晴】本题主要考查待定系数法求椭圆的标准方程、韦达定理以及解析几何中的存在性问题,属于难题.解决存在性问题,先假设存在,推证满足条件的结论,若结论正确则存在,若结论不正确则不存在,注意:①当条件和结论不唯一时要分类讨论;②当给出结论而要推导出存在的条件时,先假设成立,再推出条件;③当条件和结论都不知,按常规方法题很难时采取另外的途径.4.,点M 是x 轴上的一点,过点M 的直线l 与椭圆C 交于,A B 两点(点A 在x 轴的上方) (1)求椭圆C 的方程;(2,且直线l 与圆相切于点N ,求.【来源】【全国百强校】黑龙江省大庆实验中学2018届高三上学期期初考试数学(理)试题【答案】(12【解析】试题分析:(1)根据条件列出关于c a b ,,的方程组,方程组得224,1a b ==,(2)设直线:l x ty m =+,则根据圆心到切线距离等于半径得,有122y y =-,联立直线方程与椭圆方程,利用韦达定,三者消12y y ,得于,m t的解方程组得. 试题解析:(1,即()()24430a a --=, 又2233a b =+>,故224,1a b ==,椭圆C 的方程为(2)设(),0M m ,直线()()1122:,,,,l x ty m A x y B x y =+, ,有122y y =-,由2122122222,2y y y y y y y y =-+=-+=-,则()()221212122y y y y y y ⎡⎤=--+=-+⎣⎦,化简得()()2222448m t t m -+=-,原点O 到直线的距离又直线l 与圆,即()()2234740m m -+=,,满足0∆>,此时 在Rt OMN ∆中,5.,左右焦点分别为12,F F A 是椭圆在第一象限上的一个动点,圆C 与1F A 的延长线, 12F F 的延长线以及线段2AF 都相切,()2,0M 为一个切点.(1)求椭圆方程;(2,过2F 且不垂直于坐标轴的动点直线l 交椭圆于,P Q 两点,若以,NP NQ 为邻边的平行四边形是菱形,求直线l 的方程.【来源】【全国百强校】河北省石家庄二中2017届高三下学期第三次模拟考试数学(理)试题【答案】(12【解析】试题分析:(1)圆C 为三角形12AF F 内切圆,由内切圆性质及椭圆定义得()()222c c a -++=,即2a = 2)以,NP NQ 为邻边的平行四边形是菱形,所以()·0,NP NQ PQ += 设()()1122,,,P x y Q x y , l 方程为(2)设l 方程为 ,代入椭圆方程可得,设()()1122,,,P x y Q x y,则,以,NP NQ 为邻边的平行四边形是菱形,()·0,NP NQ PQ NP NQ x ⎛+=+=- 283233,k k ⎫-- ,PQ 的方向向量为()1,k ,, l 6.设点,A B 的坐标分别为()()5,0,5,0-,直线,AM BM 相交于点M ,且它们的斜率之积()20525b b -<<. (1)求点M 的轨迹方程;(2)在点M 的轨迹上有一点P 且点P 在x 轴的上方, 120APB ∠=︒,求b 的范围.【来源】【全国校级联考】山西实验中学、南海桂城中学2018届高三上学期联考理数试题【答案】(1)()2221525x y x b+=≠±;(2)03b <≤.【解析】试题分析:(1)设点M 的坐标为(),x y ,表示出两直线的斜率,利用斜率之积等于()20525b b -<<建立方程,化简即可求出轨迹方程;(2)点P 的坐标为()00,x y ,利用斜率公式及夹角公式,可得00,x y 的关系,再结合点在椭圆上消元后根据椭圆的范围建立不等关系,即可解出b 的范围.方法一:设点P 的坐标为()00,x y ,过点P 作PH 垂直于x 轴,垂足为H ,000055tan ,tan x x APH BPH y y +-∠=∠= 00000200020005510+tan120552511x x y y y x x x y y y +-︒==+---⋅- 因为点P 的坐标为()00,x y 在点M 的轨迹上,所以()220021525x y x b+=≠± 得202202525x y b-=0210251y b =-,20y =因为00y b <≤,20b <≤,2250b +≤.所以解得03b <≤. 方法二:设点P 的坐标为()00,x y ,点,A B 的坐标分别为()()5,0,5,0- 直线AP 的斜率()00055AP y k x x =≠+,直线BP 的斜率()00055BP yk x x =≠- 由120APB ∠=︒得0000000055tan120155y yx x y y x x --+︒=+⋅-+所以220025x y +-=(1) 又由于点P 的坐标为为()00,x y 在点M 的轨迹上,所以()220021525x y x b +=≠± 得220022525x y b -=-,代入(1)得202251y y b ⎛⎫-= ⎪⎝⎭20y =. 因为00y b <≤,20b <≤,2250b +≤.所以解得0b <≤又由于点P 的坐标为为()00,x y 在点M 的轨迹上,所以()220021525x y x b+=≠± 005,{ .x cos y bsin θθ== 代入(1)得22225cos sin 25b θθ+-=,222sin 25sin b θθ-=,225b -= 10sin 1,1sin θθ<≤≤,2225250b b -≥+-≤.所以解得0b <≤方法四:设点P 的坐标为()00,x y ,点,A B 的坐标分别为()()5,0,5,0- 直线AP 的斜率()0055AP y k x x =≠+,直线BP 的斜率()0055BP yk x x =≠- 由120APB ∠=︒得0000000055tan120155y yx x y y x x --+︒=+⋅-+所以02021025251y x b-=-(1)将220022525x y b -=-代入(1)2021025125b y b =-,)2201025b b y -=,20y =因为00y b <≤,20b <≤,2250b +≤.所以解得03b <≤. 方法五设点P 的坐标为()00,x y ,点,A B 的坐标分别为()()5,0,5,0- 直线AP 的斜率()0055AP y k x x =≠+,直线BP 的斜率()0055BP yk x x =≠- 由120APB ∠=︒得1BM AMBM AMk k k k -=+2125BM AMk k b -=-2125AM BM b k k ⎫-=-⎪⎭0,0,0AM BM BM k k k >-2125AM BM b k k ⎫-=-≥⎪⎭2125b ⎫-≥⎪⎭212255b b ⎫-≥⎪⎭2250b +≤. 所以解得0b <≤点睛:本题主要考查了轨迹方程及直线与椭圆的位置关系,是高考的必考点,属于难题.求椭圆方程的方法一般就是根据条件建立,,a b c 的方程,求出22,a b 即可,注意222,ca b c e a=+=的应用;涉及直线与圆锥曲线相交时,未给出直线时需要自己根据题目条件设直线方程,要特别注意直线斜率是否存在的问题,避免不分类讨论造成遗漏,然后要联立方程组,得一元二次方程,利用根与系数关系写出1212,x x x x +⋅,再根据具体问题应用上式,其中要注意判别式条件的约束作用.7.已知椭圆C :,且椭圆C 过点C 的左、右顶点分别为,A B ,点P 是椭圆C 上异于,A B 的点,直线21:l x a =与直线,AP BP分别交于点,M N . (1)求椭圆C 的方程;(2)过点P 作椭圆C 的切线2l ,记2l MN Q ⋂=,且MQ QN λ=,求λ的值. 【来源】河南省林州市第一中学2018届高三8月调研考试理科数学试题【答案】(1)椭圆C 的方程为(2)1λ= 【解析】试题分析:(1)由题意求得2a =, 1b =,,故椭圆C 的方程为(2)很明显直线的斜率存在,设出切线方程,联立直线与椭圆的方程,结合韦达定理得到关于实数λ 的不等式组,结合不等式组的性质和题意讨论可得1λ=. 试题解析:(1)依题意,,解得2a =, 1b =,故椭圆C 的方程为(2)依题意, ()2,0A -, ()2,0B ,直线1:4l x =,设()()000,2P x y x ≠±,则直线AP 的方程为,令4x =,得点M 的纵坐标为直线BP 的方程为,令4x =,得点N 的纵坐标为 由题知,椭圆在点P 处切线斜率存在,可设切线方程为()00y y k x x -=-, 由()0022{44y k x x y x y =-++=,得()()()2220000148440k x k y kx x y kx ++-+--=,由0∆=,得()()()2222000064161410ky kx k y kx ⎡⎤--+--=⎣⎦, 整理得: 22220000214y kx y k x k -+=+,()220041x y =-代入上式并整理得所以点P 处的切线方程为令4x =得,点Q 的纵坐标为 设MQ QN λ=,所以()Q M N Q y y y y λ-=-, 所以0016x y --=,因为022x -<<,所以1λ=.8.已知椭圆C : 22221x y a b+=(1a b >>)的左焦点F 与抛物线24y x =-的焦点重合,直线0x y -+=与以原点O 为圆心,以椭圆的离心率e 为半径的圆相切. (Ⅰ)求该椭圆C 的方程;(Ⅱ)过点F 的直线交椭圆于A , B 两点,线段AB 的中点为G , AB 的垂直平分线与x 轴和y 轴分别交于D , E 两点.记GFD ∆的面积为1S , OED ∆的面积为2S .问:是否存在直线AB ,使得12S S =,若存在,求直线AB 的方程,若不存在,说明理由.【来源】【全国市级联考】辽宁省锦州市2017届高三质量检测(二)数学(理)试题【答案】(Ⅰ)22143x y +=;(Ⅱ)见解析.试题解析:(Ⅰ)由题意,得1c =,12e ==,即12c a =,∴2a =, 1b = ∴所求椭圆C 的方程为22143x y +=. (Ⅱ)假设存在直线AB 使12S S =,显然直线AB 不能与x , y 轴垂直. ∴直线AB 的斜率存在,设其方程为()1y k x =+(0k ≠),将其代入22143x y +=整理得()22224384120k x k x k +++-=, 设()11,A x y , ()22,B x y , 2122843k x x k -+=+, ()()1212261143ky y k x k x k +=+++=+, ∴22243,4343k k G k k ⎛⎫- ⎪++⎝⎭, ∵DG AB ⊥,∴2223431443Dkk k kx k +⨯=---+, 解得2243D k x k -=+,即22,043k D k ⎛⎫- ⎪+⎝⎭,∵GFD OED ∆~∆,∴GF DGOE OD =,∴2GFDGDG OE OD OD ⎛⎫⋅= ⎪ ⎪⎝⎭, 即212DG S S OD ⎛⎫= ⎪ ⎪⎝⎭,又∵12S S =,∴GD OD =,2243k k -=+, 整理得2890k +=因为此方程无解,故不存在直线AB 满足12S S =.9.已知椭圆2222:1(0)x y C a b a b +=>>, O 是坐标原点, 12,F F 分别为其左右焦点,12F F =M 是椭圆上一点, 12F MF ∠的最大值为23π(Ⅰ)求椭圆C 的方程;(Ⅱ)若直线l 与椭圆C 交于,P Q 两点,且OP OQ ⊥ (i )求证:2211OPOQ+为定值;(ii )求OPQ ∆面积的取值范围.【答案】1.(1)2214x y +=(2)见解析试题解析:(1)由题意得2,1a b ==,得椭圆方程为: 2214x y += (2)i)当,OP OQ 斜率都存在且不为0时,设:OP l y kx =, ()()1122,,,P x y Q x y由22{14y kxx y =+=消y 得212414x k =+, 2222112414k y k x k ==+ 同理得222244k x k =+, 222222144y x k k ==+ 故2222221122111154x y x y OPOQ+=+=++ 当,OP OQ 斜率一个为0,一个不存在时,得2211115414OPOQ+=+= 综上得221154OPOQ+=,得证。
山东省实验中学2011级第二次模拟考试数学试题(理科)2014.4第I 卷(选择题 50分)一、选择题:本大题共10小题,每小题5分,共50分.在每个小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{}{}()12,1R A x x B x x A C B =-≤≤=<⋂,则= A.{}1x x > B. {}1x x ≥ C.{}2x x 1<≤ D. {}2x x 1≤≤ 2.已知直线l ⊥平面α,直线m β⊂平面,有下面四个命题:①//l m αβ⇒⊥; ②//l m αβ⊥⇒;③//l m αβ⇒⊥;④//l m αβ⊥⇒ 其中正确的两个命题是A.①②B.③④C.②④D.①③3.给出下列图象其中可能为函数()()432,,,f x x ax cx bx d a b c d R =++++∈的图象是 A.①③ B.①②C.③④D.②④ 4.已知圆()()22121111C x y C C ++-=:,圆与圆关于直线10x y --=对称,则圆2C 的方程为A.()()22221x y ++-=B.()()22221x y -++= C.()()22221x y +++= D.()()22221x y -+-= 5.已知函数()y f x =满足:①()1y f x =+;②在[)1,+∞上为增函数,若120,0x x <>,且()()12122x x f x f x +<---,则与的大小关系是A.()()12f x f x -=-B. ()()12f x f x -<-C.()()12f x f x ->-D.无法确定6.已知G 是ABC ∆的重心,点P 是GBC ∆内一点,若AP AB AC λμλμ=++,则的取值范围是 A.112⎛⎫⎪⎝⎭, B.213⎛⎫⎪⎝⎭, C.312⎛⎫⎪⎝⎭, D.()12,7.已知点(),M a b 在由不等式组002x y x y ≥⎧⎪≥⎨⎪+≤⎩确定的平面区域内,则点(),N a b a b +-所在平面区域的面积是A.4B.2C.1D.88.已知离心率为e的双曲线和离心率为2的椭圆有相同的焦点12F F P 、,是两曲线的一个公共点,若123F PF e π∠=,则等于A.2B. 2C.52D.3 9.设αβ,为锐角,那么“()22sinsin sin αβαβ+=+”是“2παβ+=”的A.充分非必要条件B.必要非充分条件C.充要条件D.既不充分也不必要条件 10.已知函数()31,0,9,0x x f x xx x ⎧+>⎪=⎨⎪+≤⎩若关于x 的方程()()22f x x a a R +=∈有六个不同的实根,则a 的取值范围是A.(]2,8B.(]2,9C.()8,9D. (]8,9二、填空题:本大题共5小题,每小题5分,共25分.11.阅读下面程序框图,则输出的数据S 为______.12.几何体的三视图如图所示(单位:m ),则该几何体的体积为________m 3.13.已知对于任意的x R ∈,不等式35x x a -+->恒成立,则实数a 的取值范围是________.14.如图,用四种不同颜色给三棱柱111ABC A B C -的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为_________(用数字做答).15.设S 为非空数集,若,x yS ∀∈,都有,,x y x y xy S +-∈,则称S 为封闭集.下列命题①实数集是封闭集; ②全体虚数组成的集合是封闭集;③封闭集一定是无限集; ④若S 为封闭集,则一定有0S ∈;⑤若S ,T 为封闭集,且满足S U T ⊆⊆,则集合U 也是封闭集.其中真命题是_________________.三、解答题:本大题共6小题,共75分.解答应写出文字说明,演算步骤或证明过程.16.(本小题满分12分)已知ABC ∆的面积为1,且满足02AB AC AB AC <⋅≤,设和的夹角为θ. (I )求θ的取值范围;(II )求函数()22sin cos 246f ππθθθ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭的最大值及取得最大值时的θ值. 17.(本小题满分12分)如图,正三棱柱111ABC A B C -的所有棱长都为2,D 为1CC 中点.(I )求证:1AB ⊥平面1A BD ;(II )求二面角1A A D B --的大小.18.(本小题满分12分)盒中装有5个乒乓球用作比赛,其中2个是旧球,另外3个是新球,新球使用后...即成为了旧球.(I )每次比赛从盒中随机抽取1个球使用,使用后...放回盒中,求第2次比赛结束后盒内剩余的新球数为2个的概率P ;(II )每次比赛从盒中随机抽取2个球使用,使用后放回盒中,设第2次比赛结束后盒内剩余的新球数为X ,求X 的分布列和数学期望.19.(本小题满分12分)已知数列{}()*n a n N ∈的前n 项和为n S ,数列n S n ⎧⎫⎨⎬⎩⎭是首项为0,公差为12的等差数列. (I )求数列{}n a 的通项公式;(II )设()()*4215n a n b n N =⋅-∈,对任意的正整数k ,将集合{}21221,,k k k b b b -+中的三个元素排成一个递增的等差数列,其公差为x d ,求数列{}k d 的通项公式.(III )对(II )中的x d ,求集合{}1,k k x d x d x Z +<<∈的元素个数.20.(本小题满分13分)已知椭圆()2222:1x y C a b a b +=>>0的两个左、右焦点分别是())12,F F ,且经过点33A ⎛ ⎝⎭.(I )求椭圆C 的方程;(II )若椭圆C 上两点M ,N 使(),0,2OM ON OA OMN λλ+=∈∆求面积的最大值.21.(本小题满分14分)已知函数()2ln ,f x x ax x a R =+-∈.(I )若函数()[]12f x 在,上是减函数,求实数a 的取值范围;(II )令()()2g x f x x =-,是否存在实数(]0,a x e ∈,当(e 是自然常数)时,函数()g x 的最小值是3,若存在,求出a 的值;若不存,说明理由;(III )当(]0,x e ∈时,证明:()2251ln 2e x x x x ->+.。

一.基础题组1.【山东省实验中学2017届高三第一次诊,11】已知函数2log ,0,()3,0,x x x f x x >⎧=⎨≤⎩则1()4f f ⎡⎤=⎢⎥⎣⎦.【答案】19考点:分段函数求值2.【湖北省黄石市2017届高三年级九月份调研,4】已知函数()221,1,1x x f x x ax x ⎧+<=⎨+≥⎩,若()()04f f a =,则实数a 等于( ) A .12 B .45C .2D .9 【答案】C 【解析】 试题分析:()()0(2)4242ff f a a a ==+=⇒=,选C.考点:分段函数求值【名师点睛】分段函数的考查方向注重对应性,即必须明确不同的自变量所对应的函数解析式是什么.函数周期性质可以将未知区间上的自变量转化到已知区间上.解决此类问题时,要注意区间端点是否取到及其所对应的函数值,尤其是分段函数结合点处函数值.3.【江西南昌市2017届摸底考试,8】若定义域为R 的函数()f x 在(4,)+∞上为减函数,且函数(4)y f x =+为偶函数,则( )A .(2)(3)f f >B .(2)(5)f f >C .(3)(5)f f >D .(3)(6)f f > 【答案】D考点:函数性质4.【山东省肥城市2017届高三上学期升级统测,9】定义在R 上的函数()f x 满足在区间[)1,1-上,(),102,015x m x f x x x --≤<⎧⎪=⎨-≤<⎪⎩, 其中m R ∈,若5922f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭,则()5f m =( ) A .85- B .25- C .35 D .75【答案】B 【解析】试题分析:因为()()11 2.f x f x T +=-⇒=所以59111213()()||22222525f f f f m m ⎛⎫⎛⎫-=⇒-=⇒-=--⇒=- ⎪ ⎪⎝⎭⎝⎭,因此()325(3)(1)1.55f m f f =-=-=-+=-选B. 考点:分段函数性质5.【河南濮阳市一高2017届高三上学期第二次检测,6】“2log (23)1x -<”是“48x >”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】A【解析】试题分析:因为2log (23)1x -<,所以3522x <<,又因为48x >,所以32x > ,所以3522x <<⇒32x >.即“2log (23)1x -<”是“48x >”的充分不必要条件,故选A. 考点:1、对数函数的性质及指数函数的性质;2、充分条件与必要条件.6.【河南濮阳市一高2017届高三上学期第二次检测,6】函数21()log (12)1f x x x =-++的定义域为( ) A .1(0,)2 B .1(,)2-∞ C .1(1,0)(0,)2- D .1(,1)(1,)2-∞-- 【答案】D考点:1、函数的定义域;2、对数函数的.7.【河南濮阳市一高2017届高三上学期第二次检测,3】下列函数中,是偶函数且在(0,)+∞上为增函数的是( )A .cos y x =B .21y x =-+ C .2log ||y x = D .xx y e e -=- 【答案】C【解析】考点:1、函数的奇偶性;2、函数的单调性.8.【河南濮阳市一高2017届高三上学期第二次检测,4】若0.2log 2a =,0.2log 3b =,0.22c =,则( )A .a b c <<B .b a c <<C .b c a <<D .a c b << 【答案】B【解析】试题分析:0.2log y x =是减函数,所以0b a <<,又0c >,所以b a c <<.故选B. 考点:1、对数函数的性质;2、指数函数的性质.9.【河南濮阳市一高2017届高三上学期第二次检测,7】若3x a =,5x b =,则45x 等于( )A . 2abB .2a bC .2a b +D .22a b +【答案】A【解析】试题分析:()22459535x x xx x a b =⨯=⨯=.故选A.考点:指数的运算.10.【河南濮阳市一高2017届高三上学期第二次检测,9】已知函数(12),1,()1log ,13x a ax f x x x ⎧-≤⎪=⎨+>⎪⎩当12x x ≠时,1212()()0f x f x x x -<-,则a 的取值范围是( )A .1(0,]3B .11[,]32C .1(0,]2D .11[,]43【答案】A考点:1、分段函数的解析式;2、分段函数的单调性及数学的转化与划归思想.11.【河南濮阳市一高2017届高三上学期第二次检测,10】若函数2()2(2)||f x x x a x a =+--在区间[-3,1]上不是单调函数,则实数a 的取值范围是 ( )A .[-4,1]B .[-3,1]C .(-6,2)D .(-6,1) 【答案】C考点:1、分段函数的单调性;2、利用导数研究分段函数的极值点.12.【江西九江地区2017届高三七校联考,2】函数229log (1)x y x -=+的定义域是( )A .(1,3)-B .(1,3]-C .(1,0)(0,3)-D .(1,0)(0,3]-【答案】D 【解析】考点:函数定义域13.【江西九江地区2017届高三七校联考,4】幂函数2268()(44)m m f x m m x -+=-+在(0,)+∞为增函数,则m 的值为( )A .1或3B .1 C.3 D .2 【答案】B 【解析】试题分析:22441,6801m m m m m -+=-+>⇒=,选B. 考点:幂函数定义及性质14.【江西九江地区2017届高三七校联考,5】已知函数||()21x f x =-+,定义函数(),0,()(),0.f x x F x f x x >⎧=⎨-<⎩则()F x 是( )A .奇函数B .偶函数C .既是奇函数,又是偶函数D .非奇非偶函数 【答案】A考点:分段函数奇偶性15.【江西九江地区2017届高三七校联考,7】若函数22()log (3)f x x ax a =--在区间(,2]-∞-上是减函数,则实数a 的取值范围是( ) A .(,4)-∞ B .(4,4]- C .(,4)[2,)-∞+∞ D .[4,4)- 【答案】D 【解析】试题分析:由题意得230x ax a -->在区间(,2]-∞-上恒成立且22a≥-,即2(2)(2)30a a ---->且4a ≥-,解得实数a 的取值范围是[4,4)-,选D.考点:复合函数单调性16.【广东海珠区2017届上学期高三综合测试(一),3】设偶函数()f x 的定义域为R ,当[0,)x ∈+∞时,()f x 是增函数,则(2),(),(3)f f f π--的大小关系是( )A .(2)()(3)f f f π-<<-B .()(2)(3)f f f π<-<-C .(2)(3)()f f f π-<-<D .(3)(2)()f f f π-<-< 【答案】C考点:1、函数的奇偶性;2、函数的单调性.17.【河北唐山市2017届上学期高三摸底考,4】设函数(),y f x x R =∈,“()y f x =是偶函数”是“()y f x =的图象关于原点对称”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】B .【解析】试题分析:当“()y f x =的图象关于原点对称”时,函数()y f x =为奇函数,所以)()(x f x f -=-,所以)()(x f x f =-,所以()y f x =是偶函数;反过来,当“()y f x =是偶函数”时不能推出“()y f x =的图象关于原点对称”例如:2x y =,此时2x y =是偶函数,其图像不关于原点对称.所以“()y f x =是偶函数”是“()y f x =的图象关于原点对称”的必要不充分条件,故应选B .18.【河北唐山市2017届上学期高三摸底考,8】设0x 是方程13xx ⎛⎫= ⎪⎝⎭的解,则0x 所在的范围是( )A .10,3⎛⎫ ⎪⎝⎭B .11,32⎛⎫ ⎪⎝⎭C .12,23⎛⎫ ⎪⎝⎭D .2,13⎛⎫⎪⎝⎭【答案】B . 【解析】试题分析:构造函数x x f x -⎪⎭⎫ ⎝⎛=31)(,所以01031)0(0>=-⎪⎭⎫⎝⎛=f ,031313131)31(213131>⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-⎪⎭⎫ ⎝⎛=f ,021312131)21(212121<⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=-⎪⎭⎫ ⎝⎛=f ,所以由零点的存在性定理可得函数x x f x-⎪⎭⎫⎝⎛=31)(在11,32⎛⎫ ⎪⎝⎭上存在零点,故应选B .考点:1、函数与方程.19.【广西南宁二中、柳州高中、玉林高中2017届高三8月联考,6】设函数311log (2),1()3,1x x x f x x -+-<⎧=⎨≥⎩,求3(7)(log 12)f f -+=( )A .8B .15C .7D .16 【答案】C 【解析】考点:分段函数.20.【湖南永州市2017届高三第一次模拟,4】若2a =,384b =,ln2c =,则( )A .c b a <<B .c a b <<C .a b c <<D .b a c <<【答案】B考点:基本函数.21.【湖北2017届百所重点校高三联考,5】“11e eb dx x≤⎰”是“函数()2,03,0xx x f x b x ⎧+>=⎨+≤⎩是在R 上的单调函数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】B 【解析】试题分析:因e e b 1lnln -≤,即2≤b ;因函数()2,03,0x x x f x b x ⎧+>=⎨+≤⎩是在R 上的单调函数,故21≤+b ,即1≤b ,故2≤b 是1≤b 的必要非充分条件,应选B.考点:充分必要条件及运用.【易错点晴】本题是一道函数的单调性和充分必要条件整合在一起的综合问题.求解这类问题时,要充分借助题设条件,先搞清楚判定哪个命题是哪个命题的条件,再将问题转换为判定在一个命题成立的前提下,另一个命题的真假问题.本题求解时,要先将不等式“11eeb dx x≤⎰”翻译成2≤b 成立的前提下,命题“函数()2,03,0x x x f x b x ⎧+>=⎨+≤⎩是在R 上的单调函数”是否成立的问题,当然这里要用到绝对值函数语指数函数的性质.验证必要性时,要考察这个命题的逆命题的真伪.显然命题不真;反之成立,故应选B.22.【江西九江地区2017届高三七校联考,13】若方程210x mx m -+-=有两根,其中一根大于2,另一根小于2的充要条件是__________. 【答案】3m >【解析】考点:二次函数实根分布23.【江西九江地区2017届高三七校联考,15】若函数3211(),22()1log,2xaxf xx x-⎧≤⎪⎪=⎨⎪>⎪⎩(0a>,且1a≠)的值域是R,则实数a的取值范围是________.【答案】2[,1)2考点:分段函数值域【名师点睛】分段函数的考查方向注重对应性,即必须明确不同的自变量所对应的函数解析式是什么.函数周期性质可以将未知区间上的自变量转化到已知区间上.解决此类问题时,要注意区间端点是否取到及其所对应的函数值,尤其是分段函数结合点处函数值.24.【广西南宁二中、柳州高中、玉林高中2017届高三8月联考,14】已知定义在R上的偶函数()f x在[0,)+∞上单调递减,且(1)0f=,则不等式(2)0f x-≤的解集是__________.【答案】(,1][3,)-∞+∞【解析】试题分析:因为()f x在R上为单调递减的偶函数,且(1)0f=,所以不等式(2)0f x-≤等价于|2|1x-≥,解得3x≥或1x≤,所以等式(2)0f x-≤的解集为(,1][3,)-∞+∞.考点:1、函数的奇偶性;2、函数的单调性;3、不等式的解法.25.【江苏南通市如东县、徐州丰县2017届10月联考,2】函数1()lg(1)1f x xx=++-的定义域是▲.【答案】()()1,11,-⋃+∞考点:定义域26.【江苏南通市如东县、徐州丰县2017届10月联考,4】设幂函数()f x kx α=的图象经过点()4,2,则k α+=▲ . 【答案】32【解析】试题分析:由题意得11,422k αα==⇒=∴32k α+=考点:幂函数定义27.【江苏南通市如东县、徐州丰县2017届10月联考,5】计算121(lg lg 25)1004--÷= ▲ .【答案】-20 【解析】试题分析:11211(lg lg 25)100lg 10204100---÷=÷=-考点:对数式运算28.【江苏南通市如东县、徐州丰县2017届10月联考,7】已知定义在R 上的奇函数()f x 满足(4)()f x f x +=,且(0,2)x ∈时2()1f x x =+,则(7)f 的值为 ▲ .【答案】2- 【解析】试题分析:(4)()T 4f x f x +=⇒=,所以(7)(1)(1) 2.f f f =-=-=-29.【江苏南通市如东县、徐州丰县2017届10月联考,8】已知()f x 为定义在R 上的偶函数,当0x ≥时,()22x f x =-,则不等式()16f x -≤的解集是 ▲ .【答案】[]2,4- 【解析】试题分析:当0x ≥时,()22xf x =-单调递增,又()33226f =-=()16|1|324f x x x ∴-⇒-≤⇒-≤≤≤考点:利用函数性质解不等式30.【四川巴中市2017届“零诊”,14】若31044=+-x x ,则=4log 3x .【答案】1±.考点:对数的运算.二.能力题组1.【山东省实验中学2017届高三第一次诊,10】已知定义在R 上的偶函数()f x 满足(4)()f x f x -=,且(1,3]x ∈-时,21cos ,13,()2,11,x x f x x x π⎧+<≤⎪=⎨⎪-<≤⎩则()()lg ||g x f x x =-的零点个数是( ) A .9 B .10C .18D .20【答案】C 【解析】试题分析:(4)()()4f x f x f x T -==-⇒=,只需考虑(0,10]x ∈上()y f x =与lg y x =交点个数,在第一个周期(0,4]x ∈上有3个交点,第二个周期(4,8]x ∈上有4个交点,在 (8,10]x ∈上有2个交点,共有9个交点,因此零点个数一共是18个,选C. 考点:函数零点【思路点睛】(1)运用函数图象解决问题时,先要正确理解和把握函数图象本身的含义及其表示的内容,熟悉图象所能够表达的函数的性质.(2)在研究函数性质特别是单调性、最值、零点时,要注意用好其与图象的关系,结合图象研究.2.【云南省、四川省、贵州省2017届高三上学期百校大联考数学,7】设e 是自然对数的底,0a >且1a ≠,0b >且1b ≠,则“log 2log a b e >”是“01a b <<<”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】B3.【河南濮阳市一高2017届高三上学期第二次检测,11】函数2()xf x x a=+的图象可能是( )A .(1)(3)B .(1)(2)(4)C .(2)(3)(4)D .(1)(2)(3)(4) 【答案】C【解析】试题分析:取0a =,可知(4)正确;取4a =-,可知(3)正确;取1a =,可知(2)正确;无论a 取何值都无法作出(1).故选C.考点:1、函数的图象和性质;2、选择题的“特殊值法”.【方法点睛】本题主要考查函数的图象和性质、选择题的“特殊值法”,属于难题.特殊值法解答选择题是高中数学一种常见的解题思路和方法,这种方法即可以提高做题速度和效率,又能提高准确性,主要适合下列题型:(1)求值问题(可将选项逐个验证);(2)求范围问题(可在选项中取特殊值,逐一排除);(3)图象问题(可以用函数性质及特殊点排除);(4)解方程、求解析式、求通项、求前n 项和公式问题等等.4.【江西九江地区2017届高三七校联考,6】已知正方体1111ABCD A B C D -的棱长为1,E 、F 分别是边1AA 、1CC 的中点,点M 是1BB 上的动点,过三点E 、M 、F 的平面与棱1DD 交于点N ,设BM x =,平行四边形EMFN 的面积为S ,设2y S =, 则y 关于x 的函数()y f x =的解析式为( )A .23()222f x x x =-+,[0,1]x ∈B .23()222f x x x =-++,[0,1]x ∈ C .3()2f x x =-,[0,1]x ∈ D .3()2f x x =-,[0,1]x ∈【答案】A考点:函数解析式5.【江西九江地区2017届高三七校联考,8】函数221x x e x y e =-的大致图象是( )A .B .C .D .【答案】A 【解析】考点:函数图像与性质【思路点睛】(1)运用函数图象解决问题时,先要正确理解和把握函数图象本身的含义及其表示的内容,熟悉图象所能够表达的函数的性质.(2)在研究函数性质特别是单调性、最值、零点时,要注意用好其与图象的关系,结合图象研究.6.【江西九江地区2017届高三七校联考,11】已知函数()f x 和(1)f x +都是定义在R 上的偶函数,若[0,1]x ∈时,1()()2x f x =,则( )A .15()()32f f ->B .15()()32f f -<C .15()()32f f -=D .19()()32f f -<【解析】试题分析:()(),(1)(1)(2)()f x f x f x f x f x f x =-+=-+⇒+=-,所以5111(2)()2,()()()()2233f x f x T f f f f +=⇒==<=-,选A.考点:函数对称性与周期性7.【广东海珠区2017届上学期高三综合测试(一),8】已知函数()ln ||f x x x =-,则()f x 的图象大致为( )【答案】A【解析】试题分析:因为0x <时()()ln f x x x =--,()f x 在(0,)+∞上递增,0x >时,1()ln ,'()1f x x x f x x=-=-,可得()f x 在(0,1)上递减,在(1,)+∞上递增,所以只有选项A 合题意,故选A.考点:1、函数的图象和性质;2、利用导数研究函数的单调性.8.【河北衡水中学2017届上学期一调,6】函数()21cos 1e xf x x ⎛⎫=-⎪+⎝⎭的图象的大致形状是( ) A . B .C .D .【答案】B考点:函数的奇偶性及函数的图象.9.【湖南永州市2017届高三第一次模拟,12】已知函数()()()11 232 [2)x x f x f x x ⎧--∈-∞⎪=⎨-∈+∞⎪⎩,,,则函数()()cos g x f x x π=-在区间[]08,内所有零点的和为( )A .16B .30C .32D .40 【答案】C 【解析】10.【湖北2017届百所重点校高三联考,8】函数2ln x x y x=的图象大致是( )A .B .C .D .【答案】D 【解析】试题分析:从题设中提供的解析式中可以看出1,0±≠x ,且当0>x 时, x x y ln =,由于x y ln 1/+=,故函数x x y ln =在区间)1,0(e 单调递减;在区间),1(+∞e单调递增.由函数图象的对称性可知应选D. 考点:函数图象的性质及运用.11.【湖北2017届百所重点校高三联考,11】设函数()()()211,ln 31f x x g x ax x =-+=-+,若对任意[)10,x ∈+∞,都存在2x R ∈,使得()()12f x g x =,则实数a 的最大值为( ) A .94 B .2 C .92D .4 【答案】A考点:函数的图象和性质及运用.12.【四川巴中市2017届“零诊”,11】定义在R 上的奇函数)(x f 和偶函数)(x g 满足:xe x g xf =+)()(,给出如下结论:①2)(x x e e x f --=且)2()1(0g f <<;②R x ∈∀,总有1)]([)]([22=-x f x g ; ③R x ∈∀,总有0)()()()(=+--x g x f x g x f ; ④R x ∈∃0,使得)()(2)2(000x g x f x f >. 其中所有正确结论的序号是( )A .①②③B .②③C .①③④D .①②③④ 【答案】A. 【解析】试题分析:由题意得,()()()2()()()()()2x x x x x xe ef x f xg x e f x g x f x g x e e eg x ---⎧+=⎪⎧+=⎪⎪⇒⎨⎨-+-=-+=+⎪⎩⎪=⎪⎩,①:1220(1)(2)222e e e e e f g ---+<=<<=,故①正确;②:2222[()][()]()()122x x x x e e e e g x f x --+--=-=,故②正确;③:()()()()()()()()0f x g x f x g x f x g x f x g x --+=-+=,故③正确;④:000000220002()()2(2)222x x x x x x e e e e e e f x g x f x ----+-=⋅⋅==,故④错误,即正确的结论为①②③,故选A.考点:函数的性质.13.【江西九江地区2017届高三七校联考,16】给出下列四个命题:①函数()log (21)1a f x x =--的图象过定点(1,0);②已知函数()f x 是定义在R 上的偶函数,当0x ≤时,()(1)f x x x =+,则()f x 的解析式为2()||f x x x =-;③函数1||1y x =-的图象可由函数1||y x =图象向右平移一个单位得到;④函数1||1y x =-图象上的点到点(0,1)距离的最小值是3.其中所有正确命题的序号是_________. 【答案】②④考点:函数性质14.【河北省衡水中学2017届高三上学期第三次调,16】已知函数()()2lg ,064,0x x f x x x x ⎧-<⎪=⎨-+≥⎪⎩,若关于x的方程()()210fx bf x -+=有8个不同根,则实数b 的取值范围是______________.【答案】1724b <≤考点:1、分段函数;2、函数的图象;3、方程的根.【方法点睛】方程解的个数问题解法:研究程)(x g 0=的实根常将参数移到一边转化为值域问题.当研究程)(x g 0=的实根个数问题,即方程)(x g 0=的实数根个数问题时,也常要进行参变分离,得到)(x f a =的形式,然后借助数形结合(几何法)思想求解;也可将方程化为形如)()(x h x f =,常常是一边的函数图像是确定的,另一边的图像是动的,找到符合题意的临界值,然后总结答案即可.15.【江苏南通市如东县、徐州丰县2017届10月联考,10】已知1a b >>,若10log log 3a b b a +=,b a a b =,则a b += ▲ . 【答案】43【解析】试题分析:因为1a b >>,所以log 1b a >,又101101log log log log 33log 33a b b b b b a a a a +=⇒+=⇒=或(舍),因此3a b =,因为b a a b =,所以3333,13,33b b b b b b b b a =⇒=>⇒==43a b +=考点:指对数式运算16.【山东省肥城市2017届高三上学期升级统测,15】已知函数()()log 01a f x x a a =>≠且和函数()sin2g x x π=,若()f x 与()g x 的图象有且只有3个交点, 则a 的取值范围是 .【答案】()11,5,973⎛⎫⎪⎝⎭考点:函数交点【思路点睛】(1)运用函数图象解决问题时,先要正确理解和把握函数图象本身的含义及其表示的内容,熟悉图象所能够表达的函数的性质.(2)在研究函数性质特别是单调性、最值、零点时,要注意用好其与图象的关系,结合图象研究.17.【湖北2017届百所重点校高三联考,16】设函数()f x 对任意实数x 满足()()1f x f x =-+,且当01x ≤≤时,()()1f x x x =-,若关于x 的方程()f x kx =有3个不同的实数根,则k 的取值范围是___________. 【答案】(){}526,1322--+【解析】试题分析:因()()1f x f x =-+,故)()2(x f x f =+,即函数)(x f 是周期为2的周期函数,画出函数函数]1,0[),(∈=x x f y 的图象,再借助函数满足的条件()()1f x f x =-+及图象的对称性,画出函数)(x f y =的图象如图,结合图象可得12+=-kx x x ,故04)1(2>-+=∆k k ,解之可得1625<<-k 或223+-=k ,故应填(){}526,1322--+.y=kx+1yx-2-1O -2-12121考点:函数的图象等有关知识的综合运用.【易错点晴】函数图象和性质是高中数学教与学中的重点和难点之一,也是高考和各级各类考试的热点内容.本题以函数零点的个数的形式将二次函数与一次函数的零点问题进行有机地整合,有效地考查和检测学生综合运用所学知识去分析问题解决问题的能力.求解时,先探求函数的周期性,再画出函数的图象,然后借助函数的图象进行分析探求建立不等式,进而求得实数k 的取值范围是(){}526,1322--+.18.【河南濮阳市一高2017届高三上学期第二次检测,15】若“m a >”是“函数11()()33x f x m =+-的图象不过第三象限”的必要不充分条件,则实数a 能取的最大整数为__________. 【答案】1-三.拔高题组1.【河北省衡水中学2017届高三摸底联考,11】已知函数()()()()()52log 11221x x f x x x -<⎧⎪=⎨--+≥⎪⎩,则关于x 的方程()()fx a a R =∈实根个数不可能为 ( )A . 2个B .3个C . 4个D .5 个 【答案】D考点:函数与方程.【名师点睛】本题考查函数与方程,属中档题;函数与方程是最近高考的热点内容之一,解决方法通常是用零点存在定理或数形结合方法求解,如本题就是将方程转化为两个函数图象交点,通过观察图象交点的个数研究方程根的个数的.2.【河北衡水中学2017届上学期一调,10】已知()11,01,22,1,x x x f x x -⎧+≤<⎪=⎨⎪≥⎩存在210x x >≥,使得()()12f x f x =,则()12x f x 的取值范围为( )A .2112⎫-⎪⎪⎣⎭B .1,12⎡⎫⎪⎢⎣⎭C .24⎫⎪⎪⎣⎭D .2212⎫-⎪⎪⎣⎭【答案】A 【解析】考点:对数函数的图象及二次函数的性质.3.【河南百校联考2017届高三9月质检,9】已知()1145279722,,,log 979x x f x a b c --⎛⎫⎛⎫=-=== ⎪ ⎪⎝⎭⎝⎭,则()()(),,f a f b f c 的大小顺序为( )A .()()()f b f a f c <<B .()()()f c f b f a <<C .()()()f c f a f b <<D .()()()f b f c f a << 【答案】B 【解析】试题分析:()22xxf x -=-为单调递增函数,而11144527997,log 09779a b c -⎛⎫⎛⎫⎛⎫==>==< ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,所以()()()f c f b f a <<,选B.考点:比较大小4.【河北邯郸2017届9月联考,12】已知函数42412sin4()22x x x f x x +++=+,则122016()()()201720172017f f f +++=( ) A .2017 B .2016 C .4034 D .4032 【答案】D .考点:1、函数的基本性质;2、函数的奇偶性;3、函数的综合应用.【思路点睛】本题主要考查了函数的基本性质、函数的奇偶性和函数的综合应用,考查学生综合知识能力,属中档题.其解题的一般思路为:首先将已知条件进行化简并得到222sin 2)21(xx x x f ++=+,并令222sin )21(xx x x g +=+,进而可判断出其奇偶性,再由奇函数的图像与性质可得出所求的结果即可.其解题的关键是正确的化简变形并判断出函数的奇偶性.5.【河南濮阳市一高2017届高三上学期第二次检测,21】(本小题满分12分)已知函数()22xxf x -=+. (1)求方程5()2f x =的根; (2)求证:()f x 在[0,)+∞上是增函数;(3)若对于任意[0,)x ∈+∞,不等式(2)()f x f x m ≥-恒成立,求实数m 的最小值. 【答案】(1)1x =或1x =-;(2)证明见解析;(3)0.(2)证明:设120x x ≤<,则211211221212(22)(12)()()22(22)022x x x x x x x x x x f x f x +-----=+-+=<, ∴12()()f x f x <,∴()f x 在[0,)+∞上是增函数. (3)由条件知2222(2)22(22)2(())2xx x x f x f x --=+=+-=-.因为(2)()f x f x m ≥-对于[0,)x ∈+∞恒成立,且()2f x ≥,2()(2)()[()]2m f x f x f x f x ≥-=-+.又0x ≥,∴由(2)知()f x 最小值为2, ∴()2f x =时,m 最小为2-4+2=0.考点:1、简单的指数方程;2、单调性的证明方法及不等式恒成立问题.【方法点晴】本题主要考查、简单的指数方程、单调性的证明方法及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:①分离参数()a f x ≤恒成立(min ()a f x ≤即可)或()a f x ≥恒成立(max ()a f x ≥即可);②数形结合(()y f x =图象在()y g x =上方即可);③讨论最值min ()0f x ≥或max ()0f x ≤恒成立;④讨论参数.本题(3)是利用方法①求得m 的最小值的.6.【河南濮阳市一高2017届高三上学期第二次检测,18】(本小题满分12分)设222()(log )2log (0)f x x a x b x =-+>.当14x =时,()f x 有最小值-1. (1)求a 与b 的值;(2)求满足()0f x <的x 的取值范围. 【答案】(1)23a b =-⎧⎨=⎩;(2)11(,)82x ∈.考点:1、二次函数配方法求最值;2、简单的对数不等式.7.【江西九江地区2017届高三七校联考,17】(本小题满分10分)设()log (1)log (3)(0,1)a a f x x x a a =++->≠,且(1)2f =. (1)求a 的值及()f x 的定义域; (2)求()f x 在区间3[0,]2上的值域. 【答案】(1)2a =,(2)215[log ,2]4【解析】试题分析:(1)由(1)2f =的log 42a =,解得2a =(2)因为22()log [(1)4]f x x =--+,所以当(1,1]x ∈-时,()f x 是增函数;当(1,3)x ∈时,()f x 是减函数.因此()f x 在区间3[0,]2上的值域是考点:函数定义域与值域8.【江西九江地区2017届高三七校联考,19】(本小题满分12分)已知二次函数()f x 的对称轴2()x f x =-,的图象被x 轴截得的弦长为3(0)1f =. (1)求()f x 的解析式;(2)若1(())2x f k >对[1,1]x ∈-恒成立,求实数k 的取值范围. 【解析】试题分析:(1)由题意可得二次函数两个零点,所以用零点式设()(23)(23)f x a x x =++,再根据(0)1f =解得1a =(2)不等式恒成立问题一般转化为对应函数最值问题min 1(())2x f k >,而求函数最值,先确定内函数值域11()[,2]22x t =∈,即为外函数定义域,再根据二次函数对称轴与定义区间位置关系得最小值由(0)11f a =⇒=,∴2()(23)(23)41f x x x x x =++=++;………………6分(2)当[1,1]x ∈-时,11()[,2]22xt =∈,………………8分 ∵()f x 开口向上,对称轴为2x =-.∴()f t 在1[,2]2t ∈上单调递增.………………9分 ∴min113()()24f t f ==.所以实数k 的取值范围是13(,)4-∞.………………12分 考点:二次函数解析式及最值【思路点睛】对于求不等式成立时的参数范围问题,在可能的情况下把参数分离出来,使不等式一端是含有参数的不等式,另一端是一个区间上具体的函数,这样就把问题转化为一端是函数,另一端是参数的不等式,便于问题的解决.但要注意分离参数法不是万能的,如果分离参数后,得出的函数解析式较为复杂,性质很难研究,就不要使用分离参数法.9.【江苏南通市如东县、徐州丰县2017届10月联考,16】(本小题满分14分)已知函数()33x x f x λ-=+⋅()R λ∈(1) 当1λ=时,试判断函数()33x x f x λ-=+⋅的奇偶性,并证明你的结论;【答案】(1) 偶函数(2) 27λ-≤考点:函数奇偶性,不等式恒成立问题【思路点睛】对于求不等式成立时的参数范围问题,在可能的情况下把参数分离出来,使不等式一端是含有参数的不等式,另一端是一个区间上具体的函数,这样就把问题转化为一端是函数,另一端是参数的不等式,便于问题的解决.但要注意分离参数法不是万能的,如果分离参数后,得出的函数解析式较为复杂,性质很难研究,就不要使用分离参数法.10.【江苏南通市如东县、徐州丰县2017届10月联考,19】(本小题满分16分)已知函数()133x x af x b+-+=+.(1) 当1a b ==时,求满足()3x f x =的x 的取值;①存在R t ∈,不等式()()2222f t t f t k -<-有解,求k 的取值范围;②若函数()g x 满足()()()12333x xf xg x -⋅+=-⎡⎤⎣⎦,若对任意x R ∈,不等式(2)()11g x m g x ⋅-≥恒成立,求实数m 的最大值. 【答案】(1) 1x =- (2) ①()1,-+∞,②6 【解析】试题分析:(1)根据+1333x x =⋅ ,可将方程()3xf x =转化为一元二次方程:()2332310x x ⋅+⋅-=,再根据指数函数范围可得133x= ,解得1x =- (2) ①先根据函数奇偶性确定a b ,值:1,3a b ==,再利用单调性定(2) 因为()f x 是奇函数,所以()()0f x f x -+=,所以1133033x x x x a ab b-++-+-++=++ 化简并变形得:()()333260x xa b ab --++-=要使上式对任意的x 成立,则30260a b ab -=-=且解得:1133a a b b ⎧==-⎧⎪⎨⎨==-⎪⎩⎩或,因为()f x 的定义域是R ,所以13a b =-⎧⎨=-⎩舍去 所以1,3a b ==, 所以()13133x x f x +-+=+ ………………………………………6分①()131********x x x f x +-+⎛⎫==-+ ⎪++⎝⎭对任意1212,,x x R x x ∈<有: ()()()()211212121222333331313131x x x x x x f x f x ⎛⎫-⎛⎫⎪-=-=⎪ ⎪++++⎝⎭⎝⎭因为12x x <,所以21330x x ->,所以()()12f x f x >,因此()f x 在R 上递减. ………………………………………8分因为()()2222f t t f t k -<-,所以2222t t t k ->-,所以440t ∆=+>,解得:1t >-,所以k 的取值范围为()1,-+∞ ………………………………………10分 ②因为()()()12333x xf xg x -⋅+=-⎡⎤⎣⎦,所以()()3323x x g x f x --=-考点:利用函数性质解不等式,不等式恒成立问题【思路点睛】利用导数研究不等式恒成立或存在型问题,首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可分离变量,构造函数,直接把问题转化为函数的最值问题。
2017年山东省潍坊市实验中学高考数学二模试卷(理科)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若集合A={x|3x﹣x2>0},集合B={x|x<1},则A∩(∁U B)等于()A.(﹣3,1]B.(﹣∞,1]C.[1,3)D.(3,+∞)2.(5分)若z=1﹣i,则复数z+在复平面上对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)已知,则sinαcosα等于()A.B.C.D.4.(5分)的值为()A.B.πC.D.15.(5分)已知α,β是两个不同平面,直线l⊂β,则“α∥β”是“l∥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.(5分)已知等比数列{a n}满足a1=3,a1+a3+a5=21,则a3+a5+a7=()A.21B.42C.63D.847.(5分)某几何体的三视图如图所示,在该几何体的体积是()A.B.C.D.8.(5分)设m,n,t都是正数,则三个数()A.都大于4B.都小于4C.至少有一个大于4D.至少有一个不小于49.(5分)如图,正方形ABCD中,M是BC的中点,若=λ+μ,则λ+μ=()A.B.C.D.210.(5分)已知点F1是抛物线C:x2=4y的焦点,点F2为抛物线C的对称轴与其准线的交点,过F2作抛物线C的切线,切点为A,若点A恰好在以F1,F2为焦点的双曲线上,则双曲线的离心率为()A.B.﹣1C.+1D.二、填空题(每题5分,满分25分,将答案填在答题纸上)11.(5分)如图是一个算法流程图,则输出的k的值是.12.(5分)将函数f(x)=sinωx(其中ω>0)的图象向右平移个单位长度,所得图象经过点(,0),则ω的最小值是.13.(5分)二项式展开式中,前三项系数依次组成等差数列,则展开式中的常数项等于.14.(5分)在约束条件下,当3≤m≤5时,目标函数z=3x+2y的最大值的取值范围是(请用区间表示).15.(5分)对于函数f(x),若存在区间A=[m,n],使得{y|y=f(x),x∈A}=A,则称函数f(x)为“同域函数”,区间A为函数f(x)的一个“同城区间”.给出下列四个函数:①f(x)=cos x;②f(x)=x2﹣1;③f(x)=|x2﹣1|;④f(x)=log2(x﹣1).存在“同域区间”的“同域函数”的序号是(请写出所有正确的序号)三、解答题:本大题共6小题,共75分.16.(12分)已知=(2λsin x,sin x+cos x),=(cos x,λ(sin x﹣cos x))(λ>0),函数f(x)=•的最大值为2.(Ⅰ)求函数f(x)的单调递减区间;(Ⅱ)在△ABC中,内角A,B,C的对边分别为a,b,c,cos A=,若f(A)﹣m>0恒成立,求实数m的取值范围.17.(12分)如图,在三棱柱ABC﹣A1B1C1中,CA=CB=AA1,∠BAA1=∠BAC=60°,点O是线段AB的中点.(Ⅰ)证明:BC1∥平面OA1C;(Ⅱ)若AB=2,A1C=,求二面角A﹣BC﹣A1的余弦值.18.(12分)某公司的两个部门招聘工作人员,应聘者从T1、T2两组试题中选择一组参加测试,成绩合格者可签约.甲、乙、丙、丁四人参加应聘考试,其中甲、乙两人选择使用试题T1,且表示只要成绩合格就签约;丙、丁两人选择使用试题T2,并约定:两人成绩都合格就一同签约,否则两人都不签约.已知甲、乙考试合格的概率都是,丙、丁考试合格的概率都是,且考试是否合格互不影响.(I)求丙、丁未签约的概率;(II)记签约人数为X,求X的分布列和数学期望EX.19.(12分)对于数列{a n}、{b n},S n为数列{a n}的前n项和,且S n+1﹣(n+1)=S n+a n+n,a1=b1=1,b n+1=3b n+2,n∈N*.(1)求数列{a n}、{b n}的通项公式;(2)令c n=,求数列{c n}的前n项和T n.20.(13分)已知椭圆C1:的离心率为,且与y轴的正半轴的交点为,抛物线C2的顶点在原点且焦点为椭圆C1的右焦点.(1)求椭圆C1与抛物线C2的标准方程;(2)过(1,0)的两条相互垂直直线与抛物线C2有四个交点,求这四个点围成四边形的面积的最小值.21.(14分)已知函数g(x)=x2+ln(x+a),其中a为常数.(1)讨论函数g(x)的单调性;(2)若g(x)存在两个极值点x1,x2,求证:无论实数a取什么值都有.2017年山东省潍坊市实验中学高考数学二模试卷(理科)参考答案与试题解析一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若集合A={x|3x﹣x2>0},集合B={x|x<1},则A∩(∁U B)等于()A.(﹣3,1]B.(﹣∞,1]C.[1,3)D.(3,+∞)【解答】解:由A中不等式变形得:x(x﹣3)<0,解得:0<x<3,即A=(0,3),∵B=(﹣∞,1),∴∁U B=[1,+∞),则A∩(∁U B)=[1,3),故选:C.2.(5分)若z=1﹣i,则复数z+在复平面上对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:z=1﹣i,则复数z+=1﹣+=1﹣+=1﹣+=.对应点(,)在第四象限.故选:D.3.(5分)已知,则sinαcosα等于()A.B.C.D.【解答】解:由,两边平方可得:1﹣2sinαcosα=,解得sinαcosα=.故选:A.4.(5分)的值为()A.B.πC.D.1【解答】解:=﹣cos x=﹣cosπ+cos=1.故选:D.5.(5分)已知α,β是两个不同平面,直线l⊂β,则“α∥β”是“l∥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解答】解:∵α,β是两个不同平面,直线l⊂β,则“α∥β”⇒“l∥α”,反之不成立.∴α,β是两个不同平面,直线l⊂β,则“α∥β”是“l∥α”的充分不必要条件.故选:A.6.(5分)已知等比数列{a n}满足a1=3,a1+a3+a5=21,则a3+a5+a7=()A.21B.42C.63D.84【解答】解:∵a1=3,a1+a3+a5=21,∴,∴q4+q2+1=7,∴q4+q2﹣6=0,∴q2=2,∴a3+a5+a7==3×(2+4+8)=42.故选:B.7.(5分)某几何体的三视图如图所示,在该几何体的体积是()A.B.C.D.【解答】解:如图所示,该几何体为四棱锥,其中P A⊥底面ABCD,作BE⊥CD,垂足为E 点,底面由直角梯形ABED与直角三角形BCE组成.则V==.故选:B.8.(5分)设m,n,t都是正数,则三个数()A.都大于4B.都小于4C.至少有一个大于4D.至少有一个不小于4【解答】解:假设三个数都小于4,∵m,n,t都是正数,则m+≥4,n+≥4,t+≥4,则三个数的和不小于12,与小于12矛盾.因此假设不成立,∴三个数中至少有一个不小于4.故选:D.9.(5分)如图,正方形ABCD中,M是BC的中点,若=λ+μ,则λ+μ=()A.B.C.D.2【解答】解:,,;∴===;∴由平面向量基本定理得:;解得;∴.故选:B.10.(5分)已知点F1是抛物线C:x2=4y的焦点,点F2为抛物线C的对称轴与其准线的交点,过F2作抛物线C的切线,切点为A,若点A恰好在以F1,F2为焦点的双曲线上,则双曲线的离心率为()A.B.﹣1C.+1D.【解答】解:设直线F2A的方程为y=kx﹣1,代入x2=4y,可得x2=4(kx﹣1),即x2﹣4kx+4=0,∴△=16k2﹣16=0,∴k=±1,∴A(2,1),∴双曲线的实轴长为AF2﹣AF1=2(﹣1),∴双曲线的离心率为=+1.故选:C.二、填空题(每题5分,满分25分,将答案填在答题纸上)11.(5分)如图是一个算法流程图,则输出的k的值是3.【解答】解:模拟程序的运行,可得S=1,k=1S=2,不满足条件S>10,k=2,S=6不满足条件S>10,k=3,S=15满足条件S>10,退出循环,输出k的值为3.故答案为:3.12.(5分)将函数f(x)=sinωx(其中ω>0)的图象向右平移个单位长度,所得图象经过点(,0),则ω的最小值是2.【解答】解:将函数y=sinωx(其中ω>0)的图象向右平移个单位长度,所得图象对应的函数为y=sinω(x﹣).再由所得图象经过点(,0),可得sinω(﹣)=sinω=0,∴ω=kπ,k∈z.故ω的最小值是2.故答案为:2.13.(5分)二项式展开式中,前三项系数依次组成等差数列,则展开式中的常数项等于7.【解答】解:展开式的通项为前三项的系数为1,,∴解得n=8所以展开式的通项为令=0得r=2所以展开式的常数项为故答案为:714.(5分)在约束条件下,当3≤m≤5时,目标函数z=3x+2y的最大值的取值范围是[7,8](请用区间表示).【解答】解:由⇒交点为A(2,0),B(4﹣m,2m﹣4),C(0,m),C'(0,4),当3≤m<4时可行域是四边形OABC,此时,7≤z≤8当4≤m≤5时可行域是△OAC'此时,z max=8故答案为:[7,8].15.(5分)对于函数f(x),若存在区间A=[m,n],使得{y|y=f(x),x∈A}=A,则称函数f(x)为“同域函数”,区间A为函数f(x)的一个“同城区间”.给出下列四个函数:①f(x)=cos x;②f(x)=x2﹣1;③f(x)=|x2﹣1|;④f(x)=log2(x﹣1).存在“同域区间”的“同域函数”的序号是①②③(请写出所有正确的序号)【解答】解:①f(x)=,x∈[0,1]时,f(x)∈[0,1],所以①存在同域区间;②f(x)=x2﹣1,x∈[﹣1,0]时,f(x)∈[﹣1,0],所以②存在同域区间;③f(x)=|x2﹣1|,x∈[0,1]时,f(x)∈[0,1],所以③存在同域区间;④f(x)=log2(x﹣1),判断该函数是否有同域区间,即判断该函数和函数y=x是否有两个交点;而根据这两个函数图象可以看出不存在交点,所以该函数不存在同域区间.故答案为:①②③.三、解答题:本大题共6小题,共75分.16.(12分)已知=(2λsin x,sin x+cos x),=(cos x,λ(sin x﹣cos x))(λ>0),函数f(x)=•的最大值为2.(Ⅰ)求函数f(x)的单调递减区间;(Ⅱ)在△ABC中,内角A,B,C的对边分别为a,b,c,cos A=,若f(A)﹣m>0恒成立,求实数m的取值范围.【解答】解:(Ⅰ)函数=λsin2x﹣λcos2x=2λ(sin2x﹣cos2x)=2λsin(2x﹣),因为f(x)的最大值为2,所以解得λ=1,则.由,可得:,,所以函数f(x)的单调减区间为,k∈Z.(Ⅱ)由.可得2b2﹣ab=b2+c2﹣a2,即b2+a2﹣c2=ab,解得,即.因为,∴,.因为恒成立,则恒成立,即m≤﹣1.17.(12分)如图,在三棱柱ABC﹣A1B1C1中,CA=CB=AA1,∠BAA1=∠BAC=60°,点O是线段AB的中点.(Ⅰ)证明:BC1∥平面OA1C;(Ⅱ)若AB=2,A1C=,求二面角A﹣BC﹣A1的余弦值.【解答】证明:(Ⅰ)连接OC,OA1,A1B.∵CA=CB,∴OC⊥AB.∵CA=AB=AA1,∠BAA1=∠BAC=60°,故△AA1B、△ABC都为等边三角形,∴OA1⊥AB,CO⊥AB,∴OA、OA1、OC两两垂直,以O为原点,OA、OA1、OC所在直线分别为x,y,z轴,建立空间直角坐标系,设CA=CB=AA1=2,则B(﹣1,0,0),C1(﹣1,,),O(0,0,0),A1(0,,0),C(0,0,),=(0,),=(0,),=(0,0,),设平面OA1C的法向量=(1,0,0),∵=0,且BC1⊄平面OA1C,∴BC1∥平面OA1C.解:(Ⅱ)∵AB=2,A1C=,∴B(﹣1,0,0),C(0,0,),A1(0,),=(1,0,),=(1,),设平面BCA1的法向量=(x,y,z),则,取x=,得,平面ABC的法向量=(0,0,1),设二面角A﹣BC﹣A1的平面角为θ,则cosθ===.∴二面角A﹣BC﹣A1的余弦值为.18.(12分)某公司的两个部门招聘工作人员,应聘者从T1、T2两组试题中选择一组参加测试,成绩合格者可签约.甲、乙、丙、丁四人参加应聘考试,其中甲、乙两人选择使用试题T1,且表示只要成绩合格就签约;丙、丁两人选择使用试题T2,并约定:两人成绩都合格就一同签约,否则两人都不签约.已知甲、乙考试合格的概率都是,丙、丁考试合格的概率都是,且考试是否合格互不影响.(I)求丙、丁未签约的概率;(II)记签约人数为X,求X的分布列和数学期望EX.【解答】解:(I)分别记事件甲、乙、丙、丁考试合格为A,B,C,D.由题意知A,B,C,D相互独立,且,.记事件“丙、丁未签约”为F,由事件的独立性和互斥性得:P(F)=1﹣P(CD)…(3分)=…(4分)(II)X的所有可能取值为0,1,2,3,4.…(5分),,,,.所以,X的分布列是:…(12分)X的数学期望…(13分)19.(12分)对于数列{a n}、{b n},S n为数列{a n}的前n项和,且S n+1﹣(n+1)=S n+a n+n,a1=b1=1,b n+1=3b n+2,n∈N*.(1)求数列{a n}、{b n}的通项公式;(2)令c n=,求数列{c n}的前n项和T n.【解答】解:(1)由S n+1﹣(n+1)=S n+a n+n,∴S n+1﹣S n=a n+2n+1,∴a n+1﹣a n=2n+1,∴a2﹣a1=2×1+1,a3﹣a2=2×2+1,a4﹣a3=2×3+1,…a n﹣a n﹣1=2(n﹣1)+1,n≥2,以上各式相加可得:a n﹣a1=2×(1+2+3+…+n﹣1)+(n﹣1),∴a n=2×+(n﹣1)+1=n2,n≥2,∴a n=n2,n≥2,当n=1时,a1=1显然成立,故a n=n2,n∈N*;∵b n+1=3b n+2,即b n+1+1=3(b n+1),b1+1=2,∴数列{b n+1}是以2为首项,以3为公比的等比数列,b n+1=2×3n﹣1,∴b n=2×3n﹣1﹣1;(2)由(1)可知:c n===,∴T n=c1+c2+…+c n=+++…+,T n=+++…+,∴T n=2++++…+﹣,=2+﹣,=﹣,∴T n=﹣,数列{c n}的前n项和T n,T n=﹣.20.(13分)已知椭圆C1:的离心率为,且与y轴的正半轴的交点为,抛物线C2的顶点在原点且焦点为椭圆C1的右焦点.(1)求椭圆C1与抛物线C2的标准方程;(2)过(1,0)的两条相互垂直直线与抛物线C2有四个交点,求这四个点围成四边形的面积的最小值.(1)设半焦距为c(c>0),由题意得,∴,【解答】解:∴椭圆C1的标准方程为.设抛物线C2的标准方程为y2=2px(p>0),则,∴p=4,∴抛物线C2的标准方程为y2=8x.(2)由题意易得两条直线的斜率存在且不为0,设其中一条直线l1的斜率为k,直线l1方程为y=k(x﹣1),则另一条直线l2的方程为,联立得k2x2﹣(2k2+8)x+k2=0,△=32k2+64>0,设直线l1与抛物线C2的交点为A,B,则,同理设直线l2与抛物线C2的交点为C,D,则,|CD|==4∴四边形的面积==,令,则t≥4(当且仅当k=±1时等号成立),.∴当两直线的斜率分别为1和﹣1时,四边形的面积最小,最小值为96.21.(14分)已知函数g(x)=x2+ln(x+a),其中a为常数.(1)讨论函数g(x)的单调性;(2)若g(x)存在两个极值点x1,x2,求证:无论实数a取什么值都有.【解答】解:(1)∵g(x)=x2+ln(x+a),∴函数的定义域为(﹣a,+∞)∴g′(x)=2x+,令2x+>0,2x2+2ax+1>0,当4a2﹣8≤0时,即﹣≤a≤时,g′(x)≥0,即函数g(x)在(﹣a,+∞)单调递增,当4a2﹣8>0时,即a>,或a<﹣时,令g′(x)=0,解得x=,或x=,①若a>,当g′(x)>0时,即x>,或﹣a<x<,函数g(x)单调递增,当g′(x)<0时,即<x<,函数g(x)单调递减,②若a<﹣,g′(x)>0,即函数g(x)在(﹣a,+∞)单调递增,综上所述:当a≤时,即函数g(x)在(﹣a,+∞)单调递增,当a>时,函数g(x)在(,+∞)或(﹣a,)上单调递增,在(,)上单调递减,(2)由(1)可知,当a>时,函数g(x)在(,+∞)或(﹣a,)上单调递增,在(,)上单调递减,x1+x2=﹣a;x1•x2=,==a2﹣﹣ln2,g()=g(﹣)=+ln;故﹣g()=(a2﹣﹣ln2)﹣(+ln)=﹣ln﹣ln2﹣;令f(a)=﹣ln﹣ln2﹣,则f′(a)=a﹣=,∵a>,∴>0;∴f(a)=﹣ln﹣ln2﹣在(,+∞)上增函数,且f()=0,故﹣ln﹣ln2﹣>0,故无论实数a取什么值都有.。
2017年山东省实验中学高考数学一模试卷(理科)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)i是虚数单位,复数,则z的共轭复数是()A.﹣1+i B.﹣i+1C.i+1D.﹣i﹣1 2.(5分)已知集合M={x|x﹣2|<1},N={x|y=},则M∩N()A.(1,2)B.(1,2]C.(2,3)D.[2,3)3.(5分)一个几何体的三视图如所示,则该几何体的体积是()A.π+4B.2π+4C.π+4D.π+24.(5分)下列说法正确的是()A.命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”B.已知y=f(x)是R上的可导函数,则“f′(x0)=0”是“x0是函数y=f(x)的极值点”的必要不充分条件C.命题“存在x∈R,使得x2+x+1<0”的否定是:“对任意x∈R,均有x2+x+1<0”D.命题“角α的终边在第一象限角,则α是锐角”的逆否命题为真命题5.(5分)已知x,y满足,且z=2x+y的最大值是最小值的4倍,则a 的值是()A.B.C.D.46.(5分)把函数y=sin(x+)图象上各点的横坐标缩短到原来的倍(纵坐标不变),再将图象向右平移个单位,那么所得图象的一条对称轴方程为()A.B.C.D.7.(5分)已知函数f(x)=e x+x,g(x)=lnx+x,h(x)=x﹣的零点依次为a,b,c,则()A.c<b<a B.a<b<c C.c<a<b D.b<a<c8.(5分)已知椭圆=1(a1>b1>0)的离心率为,双曲线=1(a2>0,b2>0)与椭圆有相同的焦点F1,F2,M是两曲线的一个公共点,若∠F1MF2=60°,则双曲线的渐进线方程为()A.y=±x B.y=±x C.y=±x D.y=±x 9.(5分)已知直线l:ax﹣y+2=0与圆M:x2+y2﹣4y+3=0的交点为A、B,点C是圆M上的一动点,设点P(0,﹣1),的最大值为()A.12B.10C.9D.810.(5分)定义在(﹣1,1)上的函数;当x∈(﹣1,0)时,f(x)>0,若,,则P,Q,R的大小关系为()A.R>Q>P B.R>P>Q C.P>R>Q D.Q>P>R二、填空题(每题5分,满分25分,将答案填在答题纸上)11.(5分)已知随机变量ξ服从正态分布N(1,σ2),若P(ξ>2)=0.15,则P(0≤ξ≤1)=.12.(5分)已知a=dx,在二项式(x2﹣)5的展开式中,含x的项的系数为.13.(5分)已知实数x∈[2,30],执行如图所示的程序框图,则输出的x不小于103的概率是.14.(5分)已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值为.15.(5分)已知函数,若存在x∈N*使得f(x)≤2成立,则实数a的取值范围为.三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)16.(12分)在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2c﹣a)cos B﹣b cos A=0.(Ⅰ)求角B的大小;(Ⅱ)求sin A+sin(C﹣)的取值范围.17.(12分)如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PE=2BE.(I)求证:平面EAC⊥平面PBC;(Ⅱ)若二面角P﹣AC﹣E的余弦值为,求直线P A与平面EAC所成角的正弦值.18.(12分)在数列{a n}(n∈N*)中,其前n项和为S n,满足.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设(k为正整数),求数列{b n}的前2n项和T2n.19.(12分)奥运会乒乓球比赛共设男子单打、女子单打、男子团体、女子团体共四枚金牌,保守估计中国乒乓球男队单打或团体获得一枚金牌的概率均为,中国乒乓球女队单打或团体获得一枚金牌的概率均为.(1)求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率;(2)记中国乒乓球队获得的金牌数为ξ,按此估计ξ的分布列和数学期望Eξ.20.(13分)已知动圆M恒过F(1,0)且与直线x=﹣1相切,动圆圆心M的轨迹记为C;直线x=﹣1与x轴的交点为N,过点N且斜率为k的直线l与轨迹C有两个不同的公共点A,B,O为坐标原点.(1)求动圆圆心M的轨迹C的方程,并求直线l的斜率k的取值范围;(2)点D是轨迹C上异于A,B的任意一点,直线DA,DB分别与过F(1,0)且垂直于x轴的直线交于P,Q,证明:为定值,并求出该定值;(3)对于(2)给出一般结论:若点,直线,其它条件不变,求的值(可以直接写出结果).21.(14分)已知函数f(x)=e ax(a≠0).(1)当时,令(x>0),求函数g(x)在[m,m+1](m>0)上的最小值;(2)若对于一切x∈R,f(x)﹣x﹣1≥0恒成立,求a的取值集合;(3)求证:.2017年山东省实验中学高考数学一模试卷(理科)参考答案与试题解析一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)i是虚数单位,复数,则z的共轭复数是()A.﹣1+i B.﹣i+1C.i+1D.﹣i﹣1【解答】解:由,得,∴z的共轭复数是i+1.故选:C.2.(5分)已知集合M={x|x﹣2|<1},N={x|y=},则M∩N()A.(1,2)B.(1,2]C.(2,3)D.[2,3)【解答】解:由M中不等式变形得:﹣1<x﹣2<1,解得:1<x<3,即M=(1,3),由N中y=,得到4﹣2x≥0,即2x≤4=22,解得:x≤2,即N=(﹣∞,2],则M∩N=(1,2],故选:B.3.(5分)一个几何体的三视图如所示,则该几何体的体积是()A.π+4B.2π+4C.π+4D.π+2【解答】解:由三视图可知几何体为半圆柱与长方体的组合体.半圆柱的底面半径为1,高为2,长方体的棱长分别为1,2,2.所以几何体的体积V=+1×2×2=π+4.故选:C.4.(5分)下列说法正确的是()A.命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”B.已知y=f(x)是R上的可导函数,则“f′(x0)=0”是“x0是函数y=f(x)的极值点”的必要不充分条件C.命题“存在x∈R,使得x2+x+1<0”的否定是:“对任意x∈R,均有x2+x+1<0”D.命题“角α的终边在第一象限角,则α是锐角”的逆否命题为真命题【解答】解:对于A,命题“若x2=1,则x=1”的否命题为:“若x2=1,则x ≠1”,不满足否命题的定义,所以A不正确;对于B,已知y=f(x)是R上的可导函数,则“f′(x0)=0”函数不一定有极值,“x0是函数y=f(x)的极值点”一定有导函数为0,所以已知y=f(x)是R上的可导函数,则“f′(x0)=0”是“x0是函数y=f(x)的极值点”的必要不充分条件,正确;对于C,命题“存在x∈R,使得x2+x+1<0”的否定是:“对任意x∈R,均有x2+x+1<0”,不满足命题的否定形式,所以不正确;对于D,命题“角α的终边在第一象限角,则α是锐角”是错误命题,则逆否命题为假命题,所以D不正确;故选:B.5.(5分)已知x,y满足,且z=2x+y的最大值是最小值的4倍,则a 的值是()A.B.C.D.4【解答】解:作出不等式组对应的平面区域如图:由z=2x+y得y=﹣2x+z,平移直线y=﹣2x+z,由图象可知当直线y=﹣2x+z经过点A时,直线的截距最大,此时z最大,由,解得即A(1,1),此时z=2×1+1=3,当直线y=﹣2x+z经过点B时,直线的截距最小,此时z最小,由,解得,即B(a,a),此时z=2×a+a=3a,∵目标函数z=2x+y的最大值是最小值的4倍,∴3=4×3a,即a=.故选:B.6.(5分)把函数y=sin(x+)图象上各点的横坐标缩短到原来的倍(纵坐标不变),再将图象向右平移个单位,那么所得图象的一条对称轴方程为()A.B.C.D.【解答】解:图象上各点的横坐标缩短到原来的倍(纵坐标不变),得到函数;再将图象向右平移个单位,得函数,根据对称轴处一定取得最大值或最小值可知是其图象的一条对称轴方程.故选:A.7.(5分)已知函数f(x)=e x+x,g(x)=lnx+x,h(x)=x﹣的零点依次为a,b,c,则()A.c<b<a B.a<b<c C.c<a<b D.b<a<c【解答】解:由f(x)=0得e x=﹣x,由g(x)=0得lnx=﹣x.由h(x)=0得x=1,即c=1.在坐标系中,分别作出函数y=e x,y=﹣x,y=lnx的图象,由图象可知a<0,0<b<1,所以a<b<c.故选:B.8.(5分)已知椭圆=1(a1>b1>0)的离心率为,双曲线=1(a2>0,b2>0)与椭圆有相同的焦点F1,F2,M是两曲线的一个公共点,若∠F1MF2=60°,则双曲线的渐进线方程为()A.y=±x B.y=±x C.y=±x D.y=±x 【解答】解:由题意设焦距为2c,椭圆长轴长为2a1,双曲线实轴为2a2,令M在双曲线的右支上,由双曲线的定义|MF1|﹣|MF2|=2a2,①由椭圆定义|MF1|+|MF2|=2a1,②又∵∠F1MF2=60°,∴|MF1|2+|MF2|2﹣2|MF1|•|MF2|cos60°=4c2,③由①②得,|MF1|=a1+a2,|MF2|=a1﹣a2,代入③,得2(a12+a22)﹣(a12﹣a22)=4c2,即a12+3a22=4c2,由,则2c2=a12,a22=c2,即有b22=c2﹣a22=c2,则渐近线方程为y=±x,即为y=±x.故选:A.9.(5分)已知直线l:ax﹣y+2=0与圆M:x2+y2﹣4y+3=0的交点为A、B,点C是圆M上的一动点,设点P(0,﹣1),的最大值为()A.12B.10C.9D.8【解答】解:由题意,圆M:x2+y2﹣4y+3=0可化为x2+(y﹣2)2=1.=|2+|≤|2|+||=2×3+4=10,故选:B.10.(5分)定义在(﹣1,1)上的函数;当x∈(﹣1,0)时,f(x)>0,若,,则P,Q,R的大小关系为()A.R>Q>P B.R>P>Q C.P>R>Q D.Q>P>R【解答】解:取x=y=0,则f(0)﹣f(0)=f(0),所以,f(0)=0,设x<y,则,所以所以f(x)>f(y),所以函数f(x)在(﹣1,1)上为减函数,由,得:取y=,,则x=,所以,因为0<,所以所以R>P>Q.故选:B.二、填空题(每题5分,满分25分,将答案填在答题纸上)11.(5分)已知随机变量ξ服从正态分布N(1,σ2),若P(ξ>2)=0.15,则P(0≤ξ≤1)=0.35.【解答】解:∵变量ξ服从正态分布N(1,σ2),∴P(ξ>1)=0.5,∴P(1≤ξ≤2)=P(ξ>1)﹣P(ξ>2)=0.35,∴P(0≤ξ≤1)=P(1≤ξ≤2)=0.35.故答案为:0.35.12.(5分)已知a=dx,在二项式(x2﹣)5的展开式中,含x的项的系数为﹣10.【解答】解:a=dx=(2x﹣x2)=2﹣1=1,二项式(x2﹣)5 =(x2﹣)5,∴二项式(x2﹣)5的展开式的通项公式为T r+1=•(﹣1)r•x10﹣3r,令10﹣3r=1,求得r=3,含x的项的系数为﹣=﹣10,故答案为:﹣10.13.(5分)已知实数x∈[2,30],执行如图所示的程序框图,则输出的x不小于103的概率是.【解答】解:设实数x∈[2,30],经过第一次循环得到x=2x+1,n=2经过第二循环得到x=2(2x+1)+1,n=3经过第三次循环得到x=2[2(2x+1)+1]+1,n=4此时输出x输出的值为8x+7令8x+7≥103得x≥12由几何概型得到输出的x不小于103的概率为P==故答案为:.14.(5分)已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值为4.【解答】解:考察基本不等式x+2y=8﹣x•(2y)≥8﹣()2(当且仅当x =2y时取等号)整理得(x+2y)2+4(x+2y)﹣32≥0即(x+2y﹣4)(x+2y+8)≥0,又x+2y>0,所以x+2y≥4(当且仅当x=2y时即x=2,y=1时取等号)则x+2y的最小值是4.故答案为:4.15.(5分)已知函数,若存在x∈N*使得f(x)≤2成立,则实数a的取值范围为(﹣∞,﹣15].【解答】解:f(x)≤2,即为≤2,由x∈N*,可得3x2+(a﹣2)x+24≤0,即有2﹣a≥=3x+,由3x+≥2 =12,当且仅当x=2∉N,由x=2可得6+12=18;x=3时,可得9+8=17,可得3x+的最小值为17,由存在x∈N*使得f(x)≤2成立,可得2﹣a≥17,解得a≤﹣15.故答案为:(﹣∞,﹣15].三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)16.(12分)在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2c﹣a)cos B﹣b cos A=0.(Ⅰ)求角B的大小;(Ⅱ)求sin A+sin(C﹣)的取值范围.【解答】解:(Ⅰ)在△ABC中,∵(2c﹣a)cos B﹣b cos A=0,∴2sin C cos B﹣sin A cos B﹣sin B cos A=0,即2sin C cos B﹣sin(A+B)=0,即sin C(2cos B﹣1)=0,∴cos B=,∴B=.(Ⅱ)由(Ⅰ)可得sin A+sin(C﹣)=sin A+cos A=2sin(A+),∵A∈(0,),∴A+∈(,),sin(A+)∈(,1],∴2sin(A+)∈(1,2],即sin A+sin(C﹣)的取值范围是(1,2].17.(12分)如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PE=2BE.(I)求证:平面EAC⊥平面PBC;(Ⅱ)若二面角P﹣AC﹣E的余弦值为,求直线P A与平面EAC所成角的正弦值.【解答】(I)证明:∵PC⊥底面ABCD,AC⊂平面ABCD,∴PC⊥AC.∵AB=2,AD=CD=1,∴AC=BC=,∴AC2+BC2=AB2,∴AC⊥BC,又BC∩PC=C,∴AC⊥平面PBC,又AC⊂平面EAC,∴平面EAC⊥平面PBC.(II)解:取AB的中点F,两角CF,则CF⊥AB,以点C为原点,建立空间直角坐标系,可得:C(0,0,0),A(1,1,0),B(1,﹣1,0),设P(0,0,a)(a>0),则E,=(1,1,0),=(0,0,a),=,取=(1,﹣1,0),则=0,∴为平面P AC的法向量.设=(x,y,z)为平面EAC的法向量,则,即,取=(a,﹣a,﹣4),∵二面角P﹣AC﹣E的余弦值为,∴===,解得a=4,∴=(4,﹣4,﹣4),=(1,1,﹣4).设直线P A与平面EAC所成角为θ,则sinθ=||===,∴直线P A与平面EAC所成角的正弦值为.18.(12分)在数列{a n}(n∈N*)中,其前n项和为S n,满足.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设(k为正整数),求数列{b n}的前2n项和T2n.【解答】解:(Ⅰ)由题设得:,所以(n≥2)所以a n=S n﹣S n=n﹣1(n≥2)﹣1当n=1时,a1=S1=0,数列{a n}是a1=0为首项、公差为1的等差数列故a n=n﹣1.(Ⅱ)由(Ⅰ)知:=.T2n=b1+b2+b3+…+b2n==.19.(12分)奥运会乒乓球比赛共设男子单打、女子单打、男子团体、女子团体共四枚金牌,保守估计中国乒乓球男队单打或团体获得一枚金牌的概率均为,中国乒乓球女队单打或团体获得一枚金牌的概率均为.(1)求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率;(2)记中国乒乓球队获得的金牌数为ξ,按此估计ξ的分布列和数学期望Eξ.【解答】解:(1)设中国乒乓球男队获0枚金牌,女队获1枚金牌为事件A,中国乒乓球男队获1枚金牌,女队获2枚金牌为事件B,则P(A+B)=P(A)+P(B)=.(2)根据题意中国乒乓球队获得金牌数是一随机变量ξ,它的所有可能取值为0,1,2,3,4(单位:枚),那么,,,,,则ξ的概率分布列为:那么,所获金牌的数学期望(枚)故中国乒乓球队获得金牌数的期望为枚.20.(13分)已知动圆M恒过F(1,0)且与直线x=﹣1相切,动圆圆心M的轨迹记为C;直线x=﹣1与x轴的交点为N,过点N且斜率为k的直线l与轨迹C有两个不同的公共点A,B,O为坐标原点.(1)求动圆圆心M的轨迹C的方程,并求直线l的斜率k的取值范围;(2)点D是轨迹C上异于A,B的任意一点,直线DA,DB分别与过F(1,0)且垂直于x轴的直线交于P,Q,证明:为定值,并求出该定值;(3)对于(2)给出一般结论:若点,直线,其它条件不变,求的值(可以直接写出结果).【解答】(1)解:由动圆M恒过F(1,0)且与直线x=﹣1相切得,点M到F (1,0)与到直线x=﹣1距离相等,∴圆心M的轨迹C的方程为:y2=4x;联立得,k2x2+(2k2﹣4)x+k2=0,∴,当k=0时,一次方程只有一个根,不成立;∴,即,解得k∈(﹣1,0)∪(0,1).∴直线l的斜率k的取值范围为k∈(﹣1,0)∪(0,1);(2)证明:设D(x0,y0),A(x1,y1),B(x2,y2),直线l DA:,即l DA:(y0+y1)y=4x+y0y1其与x=1的交点,同理l DB与x=1的交点,∴.由(1)中的x 1x2=1得,,代入上式得.故=1+4=5;(3)解:联立得,k2x2+(pk2﹣2p)x.∴,得=p2,直线l DA:,即l DA:(y0+y1)y=2px+y0y1,得,.∴=,.21.(14分)已知函数f(x)=e ax(a≠0).(1)当时,令(x>0),求函数g(x)在[m,m+1](m>0)上的最小值;(2)若对于一切x∈R,f(x)﹣x﹣1≥0恒成立,求a的取值集合;(3)求证:.【解答】解:(1)当a=时,g(x)=,则g'(x)=.当﹣1>0,即x>2时,g'(x)>0;当﹣1<0且x≠0,即x<2或0<x<2时,g'(x)<0.则g(x)的增区间为(2,+∞),减区间为(﹣∞,0),(0,2).因为m>0,所以m+1>1,①当m+1≤2,即0<m≤1时,g(x)在[m,m+1]上单调递减,所以g(x)min=g(m+1)=②当m<2<m+1,即1<m<2时,g(x)在[m,2]上单调递减,在[2,m+1]上单调递增,所以g(x)min=g(2)=③当m≥2时,g(x)在[m,m+1]上单调递增,所以g(x)min=g(m)=.综上,g(x)min=;(2)设h(x)=f(x)﹣x﹣1=e ax﹣x﹣1若a<0,则对一切x>0,h(x)<0这与题设矛盾.又a≠0,故a>0.而h'(x)=ae ax﹣1,令h'(x)=0,得x=,当x<时,h'(x)<0,h(x)单调递减;当x>时,h'(x)>0,h(x)单调递增.故当x=时,h(x)取最小值﹣﹣1.于是对一切x∈R,h(x)≥0恒成立,当且仅当﹣1≥0①令φ(x)=t﹣tlnt﹣1,则φ'(x)=﹣lnt当0<t<1时,φ'(t)>0,φ(t)单调递增;当t>1时,φ'(t)<0,φ(t)单调递减,故当t=1时,φ(t)取最大值φ(1)=0,因此,当且仅当=1,即a=1时,①式成立.综上所述,a的取值集合为{1}.(3)证明:由(2)可知,当x>0时,g(x)=,所以(x>0),可得≤于是+≤<=<.。
山东省实验中学2017级第二次模拟考试数学试题(理科)(2011.5)第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z 满足(1i)2z +=,则z 等于A .1i +B .1i -C .1i -+D .1i --2.函数21112xy +⎛⎫=⎪⎝⎭值域为A .(-∞,1)B .(12,1) C .[12,1) D .[12,+∞) 3.某调查机构对本市小学生课业负担情况进行了调查,设平均每人每天做作业的时间为x 分钟.有1000名小学生参加了此项调查,调查 所得数据用程序框图处理,若输出的结果是680,则平均每天做作 业的时间在0~60分钟内的学生的频率是 A. 680 B. 320 C. 0.68 D. 0.324.若5250125(1)(1)(1)(1)x a a x a x a x +=+-+-++- ,则0a =A .32B .1C .1-D .32- 5.等差数列{}n a 满足:296a a a +=,则9S =A .2-B .0C .1D .26.设,a b R ∈,则()sin f x x x a b =++是奇函数的充要条件是A .220a b += B .0ab = C .0ba= D .220a b -= 7.要得到函数cos(2)3y x π=+的图象,只需将函数1sin 222y x x =+的图象A .向左平移8π个单位 B .向右平移2π个单位C .向右平移3π个单位D .向左平移4π个单位8.抛物线22x y =和直线+4y x =所围成的封闭图形的面积是( )A .16B .18C .20D .229. 圆),2(01sin 12222Z ∈+≠=-+=+k k y x y x ππθθ与直线的位置关系是( )A .相离B .相切C .相交D .不能确定10.已知函数(1)y f x =+是定义域为R 的偶函数,且()f x 在[1,)+∞上单调递减,则不等式(21)(2)f x f x ->+的解集为A.{|3}x x <B.1{|3}2x x << C.1{|3}3x x -<< D.1{|3}3x x <<11.已知点P 的双曲线221169x y -=右支上 一点,12F F 、分别为双曲线的左、右焦点,I 为12PF F ∆的内心,若2121F IF IPF IPF S S S ∆∆∆+=λ成立,则λ的值为A .58B .45C .43 D .3412.已知函数3221,0()31,()468,0x x f x x x g x x x x x ⎧+>⎪=-+=⎨⎪---≤⎩,关于方程[()]0g f x a -= (a 为正实数)的根的叙述有下列四个命题①存在实数a ,使得方程恰有3个不同的实根; ②存在实数a ,使得方程恰有4个不同的实根; ③存在实数a ,使得方程恰有5个不同的实根; ④存在实数a ,使得方程恰有6个不同的实根;其中真命题的个数是A .0B .1C .2D .3第Ⅱ卷(非选择题 共90分)二、填空题:本大题共有4个小题,每小题4分,共计16分.13. 设1232,2()((2))log (1) 2.x e x f x f f x x -⎧⎪=⎨-≥⎪⎩<,则的值为,14. 当实数y x ,满足约束条件0220x y x x y a ≥⎧⎪≤⎨⎪++≤⎩(a 为常数)时y x z 3+=有最大值为12,则实数a 的值为 .15. 已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位: cm ),可得这个几何体的体积是 2cm .16. 过抛物线22y px =(0p >)的焦点F 的直线l 与抛物线在第一象限的交点为A ,与抛物线准线的交点为B ,点A 在抛物线准线上的射影为C ,若AF F B =,12BA BC ⋅=,则p的值为_____.三、解答题:本大题共6个小题.共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)在ABC ∆中,角C B A 、、所对的边分别为a 、b 、c ,且41cos =A . (Ⅰ)求A CB 2cos 2sin2-+的值; (Ⅱ)若3=a ,求bc 的最大值.18.(本小题满分12分)三棱柱111ABC A B C -,90BCA ∠=,2AC BC ==,1A 在底面ABC 上的射影恰为AC 的中点D ,又知11BA AC ⊥.(I )求证:1AC ⊥平面1A BC ; (II )求二面角1A A B C --的大小.19.(本小题满分12分)有六节电池,其中有2节没电,4节有电,每次随机抽取一个测试,不放回,直至分清楚有电没电为止,(Ⅰ)求“第二次测出的电池没电的情况下第三次测出的电池也没电”的概率。
山东省实验中学2017级第二次模拟考试
数学试题(理科)
2017.4
第I 卷(选择题 50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每个小题列出的四个选项中,选出符合题目要求的一项. 1.已知集合{}{}()12,1R A x x B x x A C B =-≤≤=<⋂,则=
A.{}1x x >
B. {}1x x ≥
C.{}2x x 1<≤
D. {}2x x 1≤≤ 2.已知直线l ⊥平面α,直线m β⊂平面,有下面四个命题: ①//l m αβ⇒⊥; ②//l m αβ⊥⇒;③//l m αβ⇒⊥;④//l m αβ⊥⇒ 其中正确的两个命题是
A.①②
B.③④
C.②④
D.①③ 3.给出下列图象
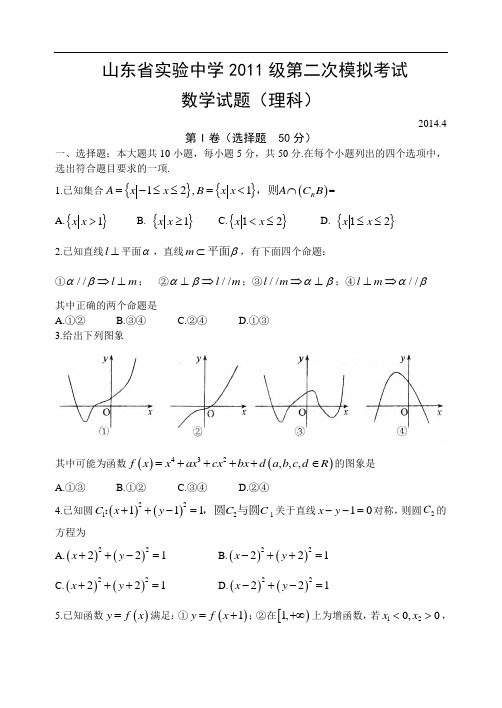
其中可能为函数()()432,,,f x x ax cx bx d a b c d R =++++∈的图象是 A.①③ B.①② C.③④ D.②④
4.已知圆()()22121111C x y C C ++-=:,圆与圆关于直线10x y --=对称,
则圆2C 的方程为
A.()()22221x y ++-=
B.()()22
221x y -++= C.()()22221x y +++= D.()()22
221x y -+-=
5.已知函数()y f x =满足:①()1y f x =+;②在[)1,+∞上为增函数,若120,0x x <>,且()()12122x x f x f x +<---,则与的大小关系是 A.()()12f x f x -=- B. ()()12f x f x -<- C.()()12f x f x ->- D.无法确定
6.已知G 是ABC ∆的重心,点P 是GBC ∆内一点,若
AP AB AC λμλμ=++
,则的取值范围是
A.112⎛⎫ ⎪⎝⎭,
B.213⎛⎫ ⎪⎝⎭,
C.3
12⎛⎫
⎪⎝⎭, D.()12,
7.已知点(),M a b 在由不等式组0
02x y x y ≥⎧⎪
≥⎨⎪+≤⎩
确定的平面区域内,则点
(),N a b a b +-所在平面区域的面积是
A.4
B.2
C.1
D.8 8.已知离心率为e
的椭圆有相同的焦点12F F P 、,是两曲线的一个公共点,若123
F PF e π
∠=
,则等于
C.52
D.3
9.设αβ,为锐角,那么“()22sin sin sin αβαβ+=+”是“2
π
αβ+=”
的
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既不充分也不必要条件
10.已知函数()31
,0
,9,0x x f x x x x ⎧+>⎪=⎨⎪+≤⎩
若关于x 的方程()()
22f x x a a R +=∈有六个不同的实根,则a 的取值范围是
A.(]2,8
B.(]2,9
C.()8,9
D. (]8,9
二、填空题:本大题共5小题,每小题5分,共25分. 11.阅读下面程序框图,则输出的数据S 为______.
12.几何体的三视图如图所示(单位:m ),则该几何体的体积为________m 3
.
13.已知对于任意的x R ∈,不等式35x x a -+->恒成立,则实数a
的取值范围是________.
14.如图,用四种不同颜色给三棱柱
111ABC A B C -的六个顶点涂色,要求四种颜
色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为_________(用数字做答).
15.设S 为非空数集,若,x y S ∀∈,都有,,x y x y xy S +-∈,则称S 为封闭集.下列命题
①实数集是封闭集; ②全体虚数组成的集合是封闭集; ③封闭集一定是无限集; ④若S 为封闭集,则一定有0S ∈; ⑤若S ,T 为封闭集,且满足S U T ⊆⊆,则集合U 也是封闭集. 其中真命题是_________________.
三、解答题:本大题共6小题,共75分.解答应写出文字说明,演算步骤或证明过程. 16.(本小题满分12分)
已知ABC ∆的面积为1,且满足02AB AC AB AC <⋅≤
,设和的夹角为θ.
(I )求θ的取值范围;
(II )求函数()22sin cos 246
f ππ
θθθ⎛⎫⎛⎫
=+-+ ⎪ ⎪⎝
⎭
⎝
⎭
的最大值及取得最大值
时的θ值.
17.(本小题满分12分)
如图,正三棱柱
111ABC A B C -的所有棱长都为2,D 为1CC 中点.
(I )求证:1AB ⊥平面1A BD ; (II )求二面角1A A D B --的大小. 18.(本小题满分12分)
盒中装有5个乒乓球用作比赛,其中2个是旧球,另外3个是新球,新球使用后...
即成为了旧球. (I )每次比赛从盒中随机抽取1个球使用,使用后...放回盒中,求第2次比赛结束后盒内剩余的新球数为2个的概率P ;
(II )每次比赛从盒中随机抽取2个球使用,使用后放回盒中,设第2次比赛结束后盒内剩余的新球数为X ,求X 的分布列和数学期望.
19.(本小题满分12分)
已知数列{}()*n a n N ∈的前n 项和为n S ,数列n S n ⎧⎫⎨⎬⎩⎭
是首项为0,公差
为12
的等差数列.
(I )求数列{}n a 的通项公式; (II )设()()*4215
n a
n b n N =
⋅-∈,对任意的正整数k ,将集合
{}21221,,k k k b b b -+中的三个元素排成一个递增的等差数列,其公差为x d ,求数列{}k d 的通项公式.
(III )对(II )中的x d ,求集合{}1,k k x d x d x Z +<<∈的元素个数. 20.(本小题满分13分)
已知椭圆()22
22:1x y C a b a b +=>>0的两个左、右焦点分别是
())
12
,F F ,且经过点33A ⎛ ⎝⎭
.
(I )求椭圆C 的方程;
(II )若椭圆C 上两点M ,N 使
(),0,2OM ON OA OMN λλ+=∈∆ 求面积的最大值.
21.(本小题满分14分) 已知函数()2ln ,f x x ax x a R =+-∈.
(I )若函数()[]12f x 在,上是减函数,求实数a 的取值范围; (II )令()()2g x f x x =-,是否存在实数(]0,a x e ∈,当(e 是自然常数)时,函数()g x 的最小值是3,若存在,求出a 的值;若不存,说明理由;
(III )当(]0,x e ∈时,证明:()225
1ln 2
e x x x x ->+.。