第五章 翼型气动特性
- 格式:ppt
- 大小:2.31 MB
- 文档页数:67




风力机叶片设计及翼型气动性能分析风力机叶片是风力发电机的核心部件之一,其设计和翼型选择对风力机的发电效率、噪音和寿命等都有着非常重要的影响。
本文将介绍风力机叶片的设计及翼型气动性能分析。
一、叶片设计原理风力机叶片的设计目的是将大气中的风能转换成旋转能,并将其通过转轴传递给发电机,从而产生电能。
因此,叶片的设计主要围绕以下几点展开:1. 创造足够的扭矩:风力机的转子需要达到一定的转速才能发电,而叶片的弯曲和扭矩对于旋转速度的影响至关重要。
设计中需要选择合适的曲线形状和长度来实现理想的扭矩和转速。
2. 保证叶片的强度和稳定性:因叶片在高速旋转状态下会受到巨大的惯性力和风力力矩的作用,因此其材料和结构要足够坚固和稳定,以避免可能的断裂等事故。
3. 提高叶片的气动效率:叶片的气动效率是指其转化风能的能力,通常可以通过优化翼型、减小阻力、降低风阻等方法来提高。
二、叶片设计步骤1. 选定叶片长度:叶片长度通常是根据风力机的规格和性能要求来确定的,也可以根据标准长度来选择。
2. 选择翼型:翼型是叶片的重要组成部分,其形状和性能决定了叶片的阻力和气动效率。
目前,常用的翼型有NACA0012、NACA4415等,根据实际需求来选择。
3. 确定叶片曲线:叶片的曲线是决定扭矩和转速的关键因素,可以通过实验或模拟方法得到合适的曲线形状。
4. 优化叶片的结构:结构设计主要涉及到叶片的强度和稳定性,通常需要进行材料选择、计算等工作以保证叶片的安全性和寿命。
5. 模拟叶片气动特性:叶片的气动特性可以通过流场模拟、试验等方式来获取,可以根据实际需求来对叶片进行调整以达到理想的效果。
三、翼型气动性能分析翼型气动性能是指翼型在气流中运动时产生的力和力矩,其中,升力和阻力是翼型气动力的主要组成部分。
通过分析翼型气动性能,可以选择最优化的翼型来设计叶片。
1. 升力和阻力翼型的升力和阻力是由翼型形状、气流速度、攻角等因素共同决定的。
实际上,翼型的气动性能曲线通常都是非线性的,其升力和阻力特性会随着攻角的变化而不断变化。
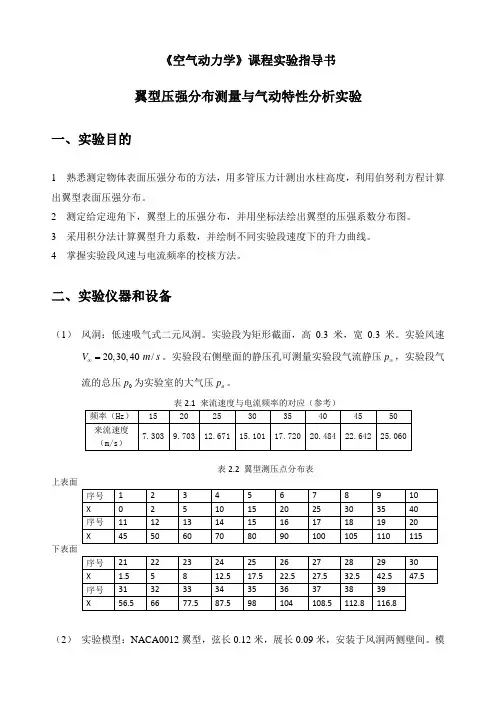
《空气动力学》课程实验指导书翼型压强分布测量与气动特性分析实验一、实验目的1 熟悉测定物体表面压强分布的方法,用多管压力计测出水柱高度,利用伯努利方程计算出翼型表面压强分布。
2 测定给定迎角下,翼型上的压强分布,并用坐标法绘出翼型的压强系数分布图。
3 采用积分法计算翼型升力系数,并绘制不同实验段速度下的升力曲线。
4 掌握实验段风速与电流频率的校核方法。
二、实验仪器和设备(1) 风洞:低速吸气式二元风洞。
实验段为矩形截面,高0.3米,宽0.3米。
实验风速20,30,40V ∞=/m s 。
实验段右侧壁面的静压孔可测量实验段气流静压p ∞,实验段气流的总压0p 为实验室的大气压a p 。
表2.1 来流速度与电流频率的对应(参考)表2.2 翼型测压点分布表上表面下表面(2) 实验模型:NACA0012翼型,弦长0.12米,展长0.09米,安装于风洞两侧壁间。
模型表面开测压孔,前缘孔编号为0,上下翼面的其它孔的编号从前到后,依次为1、2、3……。
(如表-2所示)(3) 多管压力计:压力计斜度90θ=,压力计标定系数 1.0K =。
压力计左端第一测压管通大气,为总压管,其液柱长度为I L ;左端第二测压管接风洞收缩段前的风洞入口侧壁静压孔,其液柱长度为IN L ;左端第三、四、五测压管接实验段右侧壁面的三个测压孔,取其液柱长度平均值为II L 。
其余测压管分成两组,分别与上下翼面测压孔一一对应连接,并有编号,其液柱长度为i L 。
这两组测压管间留一空管通大气,起分隔提示作用。
三、实验原理测定物体表面压强分布的意义如下:首先,根据表面压强分布,可以知道物体表面上各部分的载荷分布,这是强度设计的基本数据;其次,根据表面压强分布,可以了解气流绕过物体时的物理特性,如何判断激波,分离点位置等。
在某些风洞中(例如在二维风洞中,模型紧夹在两壁间,不便于装置天平),全靠压强分布来间接推算出作用在机翼上的升力或力矩。
测定压强分布的模型构造如下:在物体表面上各测点垂直钻一小孔,小孔底与埋置在模型内部的细金属管相通,小管的一端伸出物体外(见图1),然后再通过细橡皮管与多管压力计上各支管相接,各测压孔与多管压力计上各支管都编有号码,于是根据各支管内的液面升降高度,立刻就可判断出各测点的压强分布。





翼型气动特性数值模拟研究翼型是飞行器的重要组成部分,其气动特性(如升力、阻力、升力系数、升阻比等)对飞行器的性能有很大影响。
由于实验设备和费用的限制,气动试验成本高昂,因此数值模拟成为了研究翼型气动特性的主要方法之一。
数值模拟方法数值模拟方法主要包括计算流体力学(CFD)方法和边界元方法。
其中,CFD方法是一种利用数值计算方法处理流体动力学问题的方法,可根据所建立的数学模型,通过计算机模拟流体的运动状态,获得流体介质的相应物理量。
而边界元方法则是一种计算机辅助工具,针对问题内部的微观变化关系较弥散的情况下,仅需检查问题外缘的变化,即可通过边界元法反映问题内部变化。
两种方法的原理和适用范围存在区别。
本文主要讨论CFD方法,根据不同模型和假设,CFD方法分为欧拉方程模型、纳维—斯托克斯方程模型等。
其中,普遍认为海拔高度2000米,马赫数0.3的常温常压环境下,采用欧拉方程模型就能较为精确地预测翼型的气动特性。
欧拉方程模型及其应用欧拉方程模型的基本假设是流体为理想气体,连续性方程为无穷小量,流体的运动状态由欧拉方程控制。
其中,欧拉方程考虑了三个物理量:密度(rho)、速度(v)、热力学气压(p),并描述了它们之间的关系。
欧拉方程模型的适用范围很广,可以处理多种气流复杂情况,可以在空气、液体(如水)及其它流体的流动中预测相关的力学变量,有效地用于翼型气动特性数值模拟。
实例分析以NACA 0012翼型为例,它是由美国航空航天局设计的一支标准组合翼,被广泛应用于飞行器领域。
研究采用Ansys Fluent 15.0数值模拟软件,通过对NACA 0012翼型的气动特性的分析,验证了欧拉方程模型在预测翼型的气动特性方面的有效性。
翼型模型的几何尺寸定义采用了标准的NACA 4位数型号,其的绘制遵守了标准的绘制规则。
通常,翼型的比尺寸Re数(不能大于100万)是气动特性数值模拟的一个关键因素,它决定了模拟结果的准确度。
