正多面体

什么是多面体有哪些常见类型在我们的日常生活和数学世界中，多面体是一个常见而又有趣的概念。

那到底什么是多面体呢？简单来说，多面体是由多个平面多边形所围成的立体图形。

多面体的每个平面多边形都被称为多面体的面，两个面的公共边叫做多面体的棱，多条棱的公共顶点叫做多面体的顶点。

多面体有着各种各样的类型，下面我们就来介绍一些常见的多面体。

首先，我们来认识一下棱柱。

棱柱是一个相当常见的多面体类型。

它有两个互相平行且全等的底面，侧面都是平行四边形。

如果棱柱的底面是三角形，那就叫做三棱柱；底面是四边形，那就是四棱柱，以此类推。

比如，我们常见的长方体就是一种四棱柱，它的六个面都是矩形。

接下来是棱锥。

棱锥有一个多边形的底面，其余各面都是有一个公共顶点的三角形。

如果底面是三角形，那就是三棱锥，也叫四面体，因为它有四个面。

如果底面是四边形，那就是四棱锥。

棱锥的顶点到底面的距离叫做棱锥的高。

还有棱台，棱台可以看作是用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的部分就是棱台。

棱台的上下底面是相似的多边形。

再说说正多面体。

正多面体是指各个面都是全等的正多边形，并且各个多面角都是全等的多面角。

正多面体只有五种，分别是正四面体、正六面体（也就是正方体）、正八面体、正十二面体和正二十面体。

正四面体的四个面都是等边三角形，它是最简单也是最对称的正多面体。

正方体大家就更熟悉了，六个面都是正方形，十二条棱长度相等，八个顶点。

正八面体是由八个等边三角形围成的，它有六个顶点。

正十二面体有十二个正五边形的面，二十个顶点。

正二十面体则由二十个等边三角形组成，有十二个顶点。

多面体在我们的生活中有着广泛的应用。

在建筑设计中，许多建筑物的外形都可以看作是由不同的多面体组合而成。

比如，一些现代的体育馆、展览馆，其独特的造型往往包含了各种多面体的元素。

在包装设计中，多面体的结构也经常被运用，以达到节省材料、增加稳定性等目的。

在数学研究中，多面体的性质和相关定理也是一个重要的领域。

正十二面体折法
正十二面体是一种由 12 个面组成的正多面体，它由一个正方体切割而来。

以下是一种简单的折法:
1. 将一张方形纸对角线对折，然后展开，使对角线相交于一点。

2. 将纸张沿着相交点对折，使得纸张中心线与对角线重合。

3. 将纸张向左侧折叠一半，然后向右侧展开。

4. 将纸张向右侧折叠一半，然后向左侧展开。

5. 将纸张向上方折叠一半，然后向下方展开。

6. 将纸张向下方折叠一半，然后向上方展开。

7. 将纸张向左侧折叠一半，然后向右侧展开。

8. 将纸张向右侧折叠一半，然后向左侧展开。

9. 将纸张向上方折叠一半，然后向下方展开。

10. 将纸张向下方折叠一半，然后向上方展开。

11. 将纸张向左侧折叠一半，然后向右侧展开。

12. 将纸张向右侧折叠一半，然后向左侧展开。

完成后，正十二面体就会出现啦！。

UG6.0正多面体建模正多面体又称柏拉图立体,由欧拉定理可证明正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体共五种，均由古希腊人发现。

根据正多面的性质我用UG6.0整理出了建模方法,文中多处运用编辑对象显示和隐藏命令而又没说明，请大家不要奇怪，除此之外任一命令都有说明，有不妥之处希望大家批评指正。

1.计算法2.拉伸法一.正四面体 3.通过曲线组法4.正方体对角线法1.计算法正多面体具有高度对称性,从立体几何角度解析,很容易理解面夹角的关系,也算是从几何中找到了根本吧。

为便于分析构建了如上图正四面体线框,正四面体各面夹角相等,只要求出任两面夹角,在UG6.0中通过两次旋转,N 边曲面再缝合后便能得到正四面体.由上图知线段DF 垂直于线段AD 且∠CAD 就是面1与面2的夹角。

求出∠BAD 再乘以2就是面1与面2的夹角。

线段AB 是正四面体棱切球半径等于4/2a ,线段BD 等于内切球半径12/6a (注a 是正四面体棱长)。

所以∠BA D＝Arcsin 4/212/6a a ＝35.2644°，再乘以2等于70.5288°。

（如若计算的不够精确在UG 6.0里可能不能有效缝合)①引用几何体在草图里创建任一正三角形，而且还要确定出过中心的矢量，下一步作为矢量，角度栏里是计算的角度值。

②引用几何体③N边曲面④缝合2.拉伸法选择拉伸命令进入拉伸草图环境,画任一正三角形,完成草图。

拉伸参数如上图。

这种方法操作少面且结果直接是实体简单,只要明白70.5288度的由来,这种方法使用性更广。

3.通过曲线组在草图环境下画任一正三角形,通过派生曲线,找到三角形中心,完成草图。

建模环境下过中心画一直线垂直于正三角形且长度为边长的3/6倍,这条直线就是正四面体的高。

通过曲线组法建立的也是实体正四面体,这种方法操作起来有点小麻烦,但这种方法本身具有鲜明的特点。

4.正方体对角线法画任一正方体,连接DE,EB,BD,DG,EG,BG。

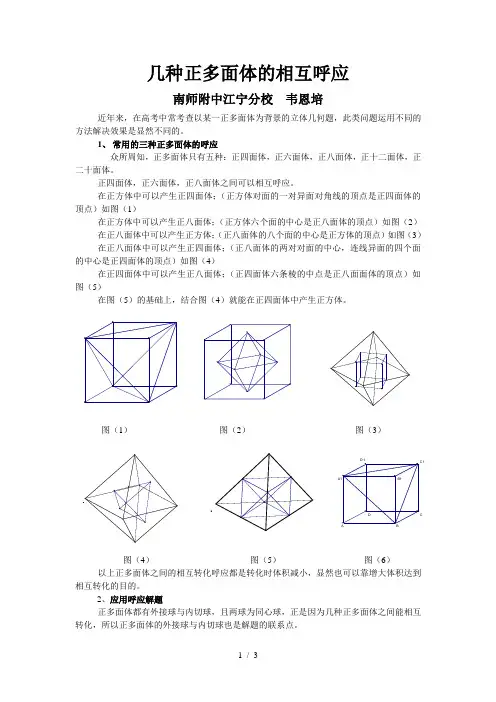
几种正多面体的相互呼应南师附中江宁分校 韦恩培近年来，在高考中常考查以某一正多面体为背景的立体几何题，此类问题运用不同的方法解决效果是显然不同的。

1、 常用的三种正多面体的呼应众所周知，正多面体只有五种：正四面体，正六面体，正八面体，正十二面体，正二十面体。

正四面体，正六面体，正八面体之间可以相互呼应。

在正方体中可以产生正四面体；（正方体对面的一对异面对角线的顶点是正四面体的顶点）如图（1）在正方体中可以产生正八面体；（正方体六个面的中心是正八面体的顶点）如图（2） 在正八面体中可以产生正方体；（正八面体的八个面的中心是正方体的顶点）如图（3） 在正八面体中可以产生正四面体；（正八面体的两对对面的中心，连线异面的四个面的中心是正四面体的顶点）如图（4）在正四面体中可以产生正八面体；（正四面体六条棱的中点是正八面面体的顶点）如图（5）在图（5）的基础上，结合图（4）就能在正四面体中产生正方体。

图（1） 图（2） 图（3）图（4）图（6）相互转化的目的。

2、应用呼应解题在高考的考查中经常会利用它们之间的相互转化而达到巧解的目的。

例1、一个四面体的所有棱长都为2，四个项点在同一球面上，则此球的表面积为（ ）A ．3πB ．4πC ．3π3D ．6π提示：利用图（1）正方体产生正四面体具有共同的外接球，即求棱长为1的正方体的外接球的表面积，易求得为π3，选A 。

例2、有一棱长为a 的正四面体骨架（架的粗细忽略不计），其内放置一气球，对其充气，使其尽可能地膨胀（成为一个球）则气球表面积的最大值为 （ ） A ．2a πB ．222a π C ．221a πD ．241a π 提示：利用图（2）正方体可以产生正八面体，正八面体可以产生正四面体知，符合条件的球即为棱长为a 22的正方体的内切球，易求得其表面积为221a π，故选C 。

例3、如图（6）棱长为a 的正方体1111D C B A ABCD -，过11BC A 的平面截去正方体一角（三棱锥111BC A B -），象这样依次截去正方体所有角，则剩下的几何体的体积为 。

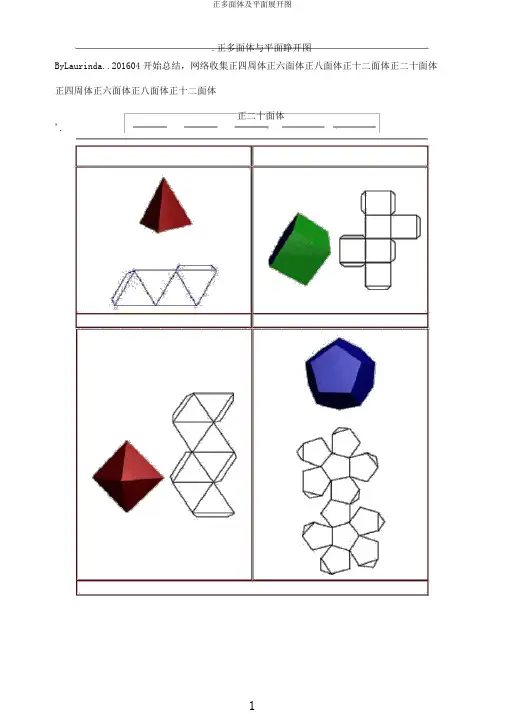
.正多面体与平面睁开图ByLaurinda..201604开始总结，网络收集正四周体正六面体正八面体正十二面体正二十面体正四周体正六面体正八面体正十二面体正二十面体'..正方体睁开图相对的两个面涂上相同颜色，正方体平面睁开图共有以下11种。

'..邻校比我们学校早了几日举行段考，拿他们的数学卷子供应给学生充做模拟考，此中有一题作图题，不好做，它要求将右图，一个由正方形和等腰直角三角形构成的五边形，以两条线切割，重构成一个等面积的等腰直角三角形。

这题让学生和我「奋战」了几节课，却老是画不可。

理论上它是能够建立的，因为等腰直角三角形能够和一个正方形等面积，并且由商高定理能够知道，存在一个正方形A，它的面积等于随意两个正方形B、C的面积和。

只需A的边长是这两个正方形B、C的边长平方和的正平方根即可。

而正方形自然能够等积于一个等腰直角三角形。

可是怎样以两条直线达成这道题呢?今日(5/19)，我利用周休持续思虑这道题，终于达成了，做法如左。

'..多面体之Euler's公式(V-E+F=2)V=极点数(numberofvertices);E=边数(numberofedges);F=面数(numberoffaces)正四周体(Tetrahedron)V=4,E=6,F=4,4-6+4=2正六面体(Cube)V=8,E=12,F=6,8-12+6=2正八面体(Octahedron)V=6,E=12,F=8,6-12+8=2正十二面体(Dodecahedron)V=20,E=30,F=12,20-30+12=2正二十面体(Icosahedron)V=12,E=30,F=20,12-30+20=2 '..BuckyballV=60,E=90,F=32(12pentagons+20hexagons),60-90+32=2增补说明：1.用Euler示性数能够证明正多面体恰巧有五种;或许假定每一极点齐集有m条线,每一条线是正n边形的一边,则因为每一正n边形的一个内角为180(n-2)/2度,围绕此极点的m个角的和小于360度,不然此极点邻近便变为一个平面,所以m[180(n-2)/n]<360,相同能够导出(m-2)(n-2)<4.2.好多病毒是正20面体(icosahedron),比如:疱疹(herpes)病毒,水痘(chickenpox)病毒 ,人体疣(humanwart)病毒,犬类传染性肝炎病毒,腺病毒(adenovirus)等.巴克球就是足球的样子,叫作"准正多面体".标尺作图正多边形正三、六边形正四、八边形正五边形直尺、圆规和量角器能够画出随意正多边形。

正多面体的制作- -
所谓正多面体是指多面体的各个面均呈全等正多边形、每个正多面体的各边的长和顶角的交角均相等。

常见正多面体有：正四面体、正六面体、正八面体、正十二面体、正二十面体，数学家尤拉(Euler)，在1752年发现各种正多面体均有的关系：面数＋顶角数＝边数＋２；学生也可经由实际折纸来「验证一下」。

制作方法：
(1) 材料：如「西卡纸」之类的厚纸板、双面胶、圆规（利用其针尖戳洞）、剪刀（或美工刀）、铅笔（或原子笔）
(2) 步骤：
1.将「各种平面展开图」（可先影印放大）覆盖于西卡纸上
2.以圆规针尖将「展开图」各顶点戳刺复制在西卡纸上
3.用铅笔将西卡纸上的各点连起来（即将「平面展开图」画出来）
4.将「平面展开图」用美工刀或剪刀裁剪下来
5.用刀背在各折线位置画上一刀，可使折纸的动作好作些
6.将各舌边内折之后贴上适当宽度的双面胶，逐一将各多面体黏合起来
多
透视图平面展开图动画
面
体
正
四
面
体
正
六
面
体
八面体
正十二面体
正二十面体
角正二十面体。

正六十四面体有哪些性质正六十四面体是一种在几何学中相对较为复杂和罕见的多面体。

要了解正六十四面体的性质，我们首先需要明确什么是多面体。

多面体是由若干个平面多边形围成的几何体。

而正多面体，则是指各个面都是全等的正多边形，并且各个多面角都是全等的多面角的多面体。

正六十四面体具有以下一些显著的性质：其一，对称性。

正六十四面体具有高度的对称性。

它的对称性不仅体现在旋转对称上，还体现在镜像对称上。

这意味着无论我们将其绕着某个轴旋转一定角度，或者通过某个平面进行镜像反射，它的外观看起来都不会发生变化。

这种对称性使得正六十四面体在美学和数学研究中都具有独特的价值。

其二，面的数量和形状。

正六十四面体拥有 64 个面。

每个面都是全等的正三角形。

这些正三角形的边长相等，内角也都相同，均为 60 度。

其三，顶点和棱的数量。

正六十四面体的顶点数量众多，棱的数量也相应不少。

通过数学计算和推导，可以得出其顶点数和棱数。

顶点数决定了多面体的结构复杂度，而棱数则反映了面与面之间的连接关系。

其四，体积和表面积。

计算正六十四面体的体积和表面积需要运用复杂的数学公式。

由于其形状的特殊性，计算过程并不简单，但通过数学方法可以得出精确的结果。

体积和表面积的数值能够帮助我们更好地理解正六十四面体的大小和规模。

其五，内角和。

正六十四面体的内角和是一个固定的值。

这个值可以通过面的数量和每个面的内角大小来计算得出。

其六，在空间中的填充性质。

正六十四面体在空间中具有一定的填充能力。

也就是说，如果我们用许多相同的正六十四面体来填充空间，可以达到一定的紧密程度。

其七，与其他正多面体的关系。

正六十四面体虽然相对复杂，但它与其他常见的正多面体，如正四面体、正六面体（正方体）、正八面体、正十二面体和正二十面体之间存在着一定的数学关联。

通过比较它们的性质和特点，可以更深入地理解多面体的多样性和统一性。

其八，数学推导和证明。

对于正六十四面体的许多性质，都可以通过严格的数学推导和证明来得出。

第八节空间正多面体前面几节我们学习了五种正多面体，以及它们在化学中的应用。

此节我们将继续对这一内容进行讨论、总结与深化。

何为正多面体，顾名思义，正多面体的每个面应为完全相同的正多边形。

对顶点来说，每个顶点也是等价的，即有顶点引出的棱的数目是相同的，相邻棱的夹角也应是一样的。

那么三维空间里的正多面体究竟有多少种呢？【例题1】利用欧拉定理（顶点数－棱边数＋面数＝2），确定三维空间里的正多面体。

【分析】从两个角度考虑：先看每个面，正多边形可以是几边形呢？我们知道三个正六边形共顶点是构成平面图形的。

因此最多只可以是正五边形，当然还有正三角形和正方形；再看顶点，每个顶点至少引出三条棱边，最多也只有五条棱边（六条棱边时每个角应小于60°，不存在这样的正多边形）。

因此，每个面是正五边形时，三棱共顶点；正方形时，也只有三棱共顶点（四个正方形共顶点是平面的）；正三角形时，可三棱、四棱、五棱共顶点（六个正三角形共顶点也是平面的），当然也可以说，一顶点引出三条棱边时可以为正三角形面、正方形面和正五边形面；一顶点引出四条棱边时只可以为正三角形面；一顶点引出五条棱边时也只可以为正三角形面——共计五种情况，是否各种情况都存在呢？（显然是，各种情况前面均已讨论）我们用欧拉定理来计算。

①正三角形，三棱共顶点：设面数为x，则棱边数为3x/2（一面三棱，二面共棱），顶点数为x（一面三顶点，三顶点共面），由欧拉定理得x－3x/2＋x＝2，解得x＝4，即正四面体；②正三角形，xx顶点：同理，3x/4－2x＋x＝2，解得x＝8，即正八面体；③正三角形，五棱共顶点：同理，3x/5－3x/2＋x＝2，解得x＝20，即正二十面体；④正方形，三棱共顶点：同理，4x/3－2x＋x＝2，解得x＝6，即正方体；⑤正五边形，三棱共顶点：同理，5x/3－5x/2＋x＝2，解得x＝12，即正十二面体。

【解答】共存在五种正多面体，分别是正四面体、正方体、正八面体、正十二面体、正二十面体。