利用导数探究方程根的个数问题优秀课件
- 格式:ppt
- 大小:406.00 KB
- 文档页数:23

第06讲利用导数研究函数的零点(方程的根)(精讲+精练)目录第一部分:知识点精准记忆第二部分:课前自我评估测试第三部分:典型例题剖析高频考点一:判断、证明或讨论函数零点的个数高频考点二:证明唯一零点问题高频考点三:根据零点情况求参数①利用最值(极值)研究函数零点问题②利用数形结合法研究函数的零点问题③构造函数研究函数零点问题第四部分:高考真题感悟第五部分:第06讲利用导数研究函数的零点(方程的根)(精练)1、函数的零点(1)函数零点的定义:对于函数()y f x=,把使()0f x=的实数x叫做函数()y f x=的零点.(2)三个等价关系方程0)(=xf有实数根⇔函数)(xfy=的图象与x轴有交点的横坐标⇔函数)(xfy=有零点.2、函数零点的判定如果函数()y f x=在区间[,]a b上的图象是连续不断的一条曲线,并且有()()0f a f b⋅<,那么函数()y f x=在区间(,)a b内有零点,即存在(,)c a b∈,使得()0f c=,这个c也就是()0f x=的根.我们把这一结论称为函数零点存在性定理.注意:单调性+存在零点=唯一零点1.(2022·全国·高二)已知函数()f x的定义域为[]15-,,部分对应值如下表:()f x的导函数()y f x='的图象如图所示,则下列关于函数()f x的命题:① 函数()y f x=是周期函数;② 函数()f x在[]02,是减函数;③ 如果当[]1,x t∈-时,()f x的最大值是2,那么t的最大值为4;④ 当12a<<时,函数()y f x a=-有4个零点.其中真命题的个数是A.4个B.3个C.2个D.1个2.(2022·甘肃·金昌市教育科学研究所高三阶段练习(文))已知函数()2e1xf x x a=+-()a R∈有两个极值点,则实数a的取值范围为()A.1,0e⎛⎫- ⎪⎝⎭B.2,0e⎛⎫- ⎪⎝⎭C.1,e⎛⎫-+∞⎪⎝⎭D.2,e⎛⎫-+∞⎪⎝⎭3.(2022·全国·高二)若函数()3239f x x x x m =--+仅有一个零点,则实数m 的取值范围是( )A .()5,-+∞B .(,27)(5,)-∞-⋃+∞C .(,27)-∞D .(,5)(27,)-∞-⋃+∞4.(2022·甘肃武威·模拟预测(文))函数()326f x x x m =-+有三个零点,则实数m 的取值范围是( )A .(﹣4,4)B .[﹣4,4]C .(﹣∞,﹣4]∪[4,+∞)D .(﹣∞,﹣4)∪(4,+∞)5.(2022·江苏淮安·高二期末)已知函数()e x f x =与()1g x x =+,则它们的图象交点个数为( )A .0B .1C .2D .不确定高频考点一:判断、证明或讨论函数零点(根)的个数1.(2022·全国·高二)设函数f (x )=13x -ln x ,则函数y =f (x )( )A .在区间1(,1)e,(1,e )内均有零点 B .在区间1(,1)e,(1,e )内均无零点C .在区间1(,1)e 内有零点,在区间(1,e )内无零点D .在区间1(,1)e 内无零点,在区间(1,e )内有零点2.(2022·全国·高三专题练习(文))已知函数()()12xx e f x e=-+,其中e 为自然对数的底数, 2.7182818e =……,则()f x 的零点个数为( ) A .0B .1C .2D .33.(2022·全国·高三专题练习(理))函数()()1ln 03f x x x x =->的零点个数为( )A .0B .1C .2D .34.(2022·全国·高二课时练习)求函数3()231f x x x =-+零点的个数为( ) A .1B .2C .3D .45.(2022·江苏淮安·高二期末)已知函数()e x f x =与()1g x x =+,则它们的图象交点个数为( )A .0B .1C .2D .不确定6.(2022·江苏苏州·模拟预测)方程3269100x x x -+-=的实根个数是______ .7.(2022·全国·高三专题练习)函数()1x f x e x =-+的零点个数是__________.8.(2022·广东佛山·高二阶段练习)已知函数()()1ln 2af x x a x x=+---,其中R a ∈. (1)若()f x 存在唯一极值点,且极值为0,求a 的值; (2)若2e a <,讨论()f x 在区间2[1,e ]上的零点个数.9.(2022·新疆·乌苏市第一中学高二阶段练习(文))给定函数()()1e xf x x =+.(1)判断函数()f x 的单调性,并求出()f x 的极值; (2)求出方程()()f x a a R =∈的解的个数.高频考点二:证明唯一零点(根)问题1.(2022·山西省长治市第二中学校高二阶段练习)已知函数321()(1)3=-++f x x a x x .(1)若1a =,求()f x 的单调区间及相应区间上的单调性; (2)证明:()f x 只有一个零点.2.(2022·陕西渭南·高二期末(文))已知函数()ln x axf x x+=,R a ∈. (1)若0a =,求()f x 的最大值;(2)若01a <<,求证:()f x 有且只有一个零点.3.(2022·广西玉林·模拟预测(文))已知函数217()ln 4,()2ln 22f x x x xg x x x =-=++. (1)求函数()f x 的最小值;(2)证明:函数()()()h x f x g x =+仅有一个零点.高频考点三:根据零点(根)情况求参数①利用最值(极值)研究函数零点(根)问题1.(2022·重庆市万州第二高级中学高二阶段练习)已知函数32()34f x x ax bx =+++在1x =-时有极值0. (1)求函数()f x 的解析式;(2)记()()21g x f x k =-+,若函数()g x 有三个零点,求实数k 的取值范围.2.(2022·山东师范大学附中高二阶段练习)已知函数()21xx x f x e+-=. (1)求函数()f x 的单调区间;(2)若函数()y f x a =-(a 为常数)有3个不同的零点,求实数a 的取值范围.3.(2022·宁夏六盘山高级中学高二阶段练习(理))已知函数3()91f x ax x =-+,0a >. (1)若3a =,求函数()f x 的极值;(2)若函数()f x 恰有三个零点,求实数a 的取值范围.4.(2022·北京丰台·一模)已知函数()f x = (1)当1a =时,求曲线()y f x =的斜率为1的切线方程; (2)若函数2()()3ag x f x =-恰有两个不同的零点,求a 的取值范围.5.(2022·广西桂林·二模(理))已知函数()()()211e 2xf x x ax a R =--∈ (1)讨论()f x 的单调性;(2)若()f x 有两个零点,求实数a 的取值范围.②利用数形结合法研究函数的零点(根)问题1.(2022·宁夏·银川二中高二期末(理))已知函数ln ()xf x x= (1)填写函数()f x 的相关性质;2.(2022·四川·阆中中学高二阶段练习(文))设函数3()65f x x x x R =-+∈,. (1)求函数()f x 的单调区间;(2)若关于x 的方程()f x a =有三个不等实根,求实数a 的取值范围.3.(2022·全国·信阳高中高三阶段练习(理))已知函数()2e xf x a x =-(R a ∈,e 为自然对数的底数).(1)若()0f x =有两个不相等的实数根,求a 的取值范围;4.(2022·四川·雅安中学高二阶段练习(文))已知函数()322f x x ax bx =++-在2x =-时取得极值,且在点()()1,1f --处的切线的斜率为3- . (1)求()f x 的解析式;(2)若函数()y f x λ=-有三个零点,求实数λ的取值范围.5.(2022·全国·模拟预测(理))已知函数()()2x x f x e ae a =+∈R(1)讨论()f x 的单调性;(2)设()()21x g x a x e x =-+,若方程()()g x f x =有三个不同的解,求a 的取值范围.6.(2022·四川绵阳·二模(文))已知函数()2()ln 1R f x x ax a =+-∈(1)当2a =时,求函数()f x 的单调区间;(2)若函数()f x 有且只有一个零点,求实数a 的取值范围.③构造函数研究函数零点(根)问题1.(2022·江苏宿迁·高二期末)已知函数()e xf x =(e 为自然对数的底数),()sing x a x =(,22x ππ⎡⎤∈-⎢⎥⎣⎦),a R ∈.(1)若直线:l y kx =与函数()f x ,()g x 的图象都相切,求a 的值; (2)若方程()()f x g x =有两个不同的实数解,求a 的取值范围.2.(2022·重庆南开中学高二期末)已知函数()()2ln ,f x x x g x x ax b ==++.(1)若()f x 与()g x 在1x =处有相同的切线,求实数,a b 的取值;(2)若2b =时,方程()()f x g x =在()1,+∞上有两个不同的根,求实数a 的取值范围.3.(2022·四川·成都七中高三阶段练习(理))已知函数()(1)f x a x =-,()e (1)x g x bx =-,R a ∈. (1)当2b =时,函数()()y f x g x =-有两个零点,求a 的取值范围; (2)当b a =时,不等式()()f x g x >有且仅有两个整数解,求a 的取值范围.4.(2022·全国·高三阶段练习)已知函数()()11ln e f x a x x=+++,()()e x g x x a a =++∈R .(1)试讨论函数()f x 的单调性;(2)若当1≥x 时,关于x 的方程()()f x g x =有且只有一个实数解,求实数a 的取值范围.5.(2022·河南·三模(理))已知函数()()ln 1f x x =+,()e 1xg x =-.(1)判断函数()()()h x f x g x =-的零点个数;6.(2022·江苏南京·高三开学考试)已知函数()(1)x f x e a x =+-,()sin cos g x ax x x =++ (1)求函数()f x 的最值;(2)令()()()h x f x g x =-,求函数()h x 在区间(,)4π-+∞上的零点个数,并说明理由.1.(2021·全国·高考真题(理))已知0a >且1a ≠,函数()(0)a x x f x x a=>.(1)当2a =时,求()f x 的单调区间;(2)若曲线()y f x =与直线1y =有且仅有两个交点,求a 的取值范围.2.(2021·全国·高考真题)已知函数2()(1)x f x x e ax b =--+. (1)讨论()f x 的单调性;(2)从下面两个条件中选一个,证明:()f x 只有一个零点 ①21,222e a b a <≤>;②10,22a b a <<≤.3.(2021·浙江·高考真题)设a ,b 为实数,且1a >,函数()2R ()x f x a bx e x =-+∈(1)求函数()f x 的单调区间;(2)若对任意22b e >,函数()f x 有两个不同的零点,求a 的取值范围;(3)当a e =时,证明:对任意4b e >,函数()f x 有两个不同的零点()1221,,x x x x >,满足2212ln 2b b ex x e b>+.(注: 2.71828e =⋅⋅⋅是自然对数的底数)一、单选题1.(2022·江苏·南京师大附中高三开学考试)已知a ∈R ,则函数()()32113f x x a x x =-++零点的个数为( )A .1B .2C .3D .与a 有关2.(2022·浙江省浦江中学高二阶段练习)已知函数()22x f x xe x x m =---在()0,∞+上有零点,则m 的取值范围是( )A .)21ln 2,-+∞⎡⎣B .)2ln 21,--+∞⎡⎣C .)2ln 2,-+∞⎡⎣D .21ln 2,2-+∞⎡⎫⎪⎢⎣⎭3.(2022·全国·高二)函数32()2f x x x x =-++-的零点个数及分布情况为( ) A .一个零点,在1,3⎛⎫-∞- ⎪⎝⎭内B .二个零点,分别在1,3⎛⎫-∞- ⎪⎝⎭,()0,∞+内C .三个零点,分别在1,3⎛⎫-∞- ⎪⎝⎭,1,03⎛⎫- ⎪⎝⎭,()1,+∞内D .三个零点,分别在1,3⎛⎫-∞- ⎪⎝⎭,()0,1,()1,+∞内4.(2022·全国·高二)直线y a =与函数33y x x =-的图象有三个不同的交点,则实数a 的取值范围为( ) A .(2,2)-B .[2,2]-C .[2,)+∞D .(,2]-∞-5.(2022·全国·高二)已知函数20()210x e x f x x x x -⎧≤=⎨--+>⎩,若函数()()g x f x kx =-有两个零点,则实数k 等于(e 为自然对数的底数)( ) A .e -B .1-C .2D .2e6.(2022·河南·襄城高中高二阶段练习(理))已知函数()2ln f x x =,()322g x x ex ax =-+,其中e 为自然对数的底数,若方程()()f x g x =存在两个不同的实根,则a 的取值范围为( ) A .2,e ⎛⎫-∞ ⎪⎝⎭B .22,e e ⎛⎫-∞+ ⎪⎝⎭C .()2,e -∞D .22,e e ⎛⎫-∞- ⎪⎝⎭7.(2022·江西·高三阶段练习(理))已知函数22()2(2)e (1)e x x f x a a x x =+-++有三个不同的零点123,,x x x ,且1230x x x <<<,则3122312222e e e x x x x x x ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的值为( )A .3B .6C .9D .368.(2022·全国·高三专题练习)已知方程|ln |2x kx =+在区间()50,e 上恰有3个不等实数根,则实数k 的取值范围是( ) A .5331,e e ⎛⎫ ⎪⎝⎭B .5331,e e ⎡⎫⎪⎢⎣⎭C .4221,e e ⎛⎫ ⎪⎝⎭D .4221,e e ⎡⎫⎪⎢⎣⎭二、填空题9.(2022·河南焦作·二模(理))函数1()e ln 1x f x a x -=--在(0,)+∞上有两个零点,则实数a 的取值范围是_______. 10.(2022·贵州遵义·高三开学考试(文))已知函数()3112,21ln ,2x m x f x x x m x ⎧--<⎪⎪=⎨⎪-≥⎪⎩恰有3个零点,则m 的取值范围是________.11.(2022·浙江·镇海中学高二期末)已知不等式21e 0x x a +-≥有且只有两个整数解,则实数a 的范围为___________.12.(2022·全国·高二)已知函数3211()(2)1()32xf x ax ax e x a R =---+∈在区间1,22⎛⎫ ⎪⎝⎭上有3个不同的极值点,则实数a的取值范围是__________. 三、解答题13.(2022·河南·栾川县第一高级中学高二阶段练习(理))已知()2()e ()x f x x a a =+∈R .(1)若2是函数()f x 的极值点,求a 的值,并判断2是()f x 的极大值点还是极小值点; (2)若关于x 的方程()2ln e x f x x =在1,22⎡⎤⎢⎥⎣⎦上有两个不同的实数根,求实数a 的取值范围.参考数据:ln 20.693≈14.(2022·陕西宝鸡·二模(文))已知函数()1e x f x ax =--,a ∈R . (1)讨论函数()f x 的单调性;(2)若方程()ln f x x x =在(1,e)上有实根,求实数a 的取值范围.15.(2022·河南·沈丘县第一高级中学高二期末(文))已知函数()ln f x x =. (1)当[)1,x ∞∈+时,证明:函数()f x 的图象恒在函数()322132=-g x x x 的图象的下方; (2)讨论方程()0f x kx +=的根的个数.16.(2022·吉林·长春外国语学校高二阶段练习)若函数()32113f x x ax bx =++-,当2x =时,函数()f x 有极值13-.(1)求函数的解析式;(2)若关于x 的方程()f x k =有三个解,求实数k 的取值范围.17.(2022·浙江浙江·二模)已知函数2()ln (2)f x x a x a =+<. (1)若2a =-,求函数()f x 的极小值点;(2)当2(]0,x ∈时,讨论函数()f x 的图象与函数(2)22y a x a =+--的图象公共点的个数,并证明你的结论.。


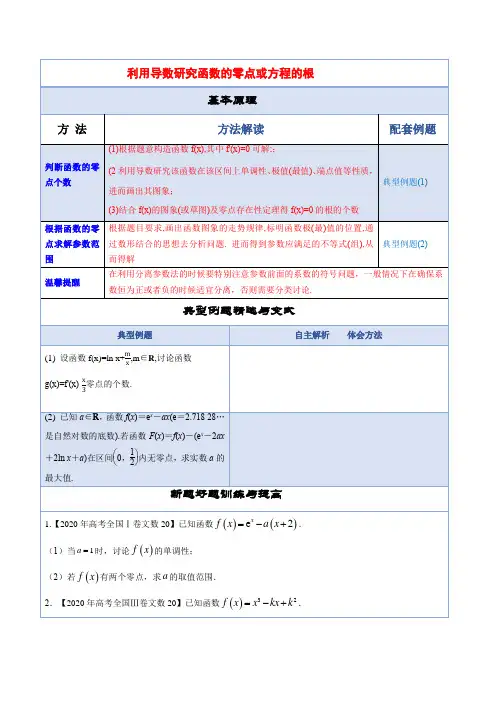
参考答案(1)函数g (x )=f '(x )-x3=1x −mx 2−x3(x >0). 令g (x )=0,得m =-13x 3+x (x >0).设h (x )=-13x 3+x (x ≥0),∴h '(x )=-x 2+1=-(x -1)(x +1). 当x ∈(0,1)时,h '(x )>0,此时h (x )在(0,1)内单调递增; 当x ∈(1,+∞)时,h '(x )<0,此时h (x )在(1,+∞)内单调递减. ∴当x =1时,h (x )取得极大值h (1)=-13+1=23.令h (x )=0,即-13x 3+x =0,解得x =0或x =√3.函数h (x )的图象如图所示.由图可知:①当m >23时,函数y =m 和函数y =g (x )的图象无交点; ②当m =23时,函数y =m 和函数y =g (x )的图象有且仅有一个交点;③当0<m <23时,函数y =m 和函数y =g (x )的图象有两个交点;④当m ≤0时,函数y =m 和函数y =g (x )的图象有且仅有一个交点.综上所述,当m >23时,函数g (x )无零点;当m =23或m ≤0时,函数g (x )有且仅有一个零点;当0<m <23时,函数g (x )有两个零点.当4027k <<时,3k k >,且2()0f k k =>,∴()f x 在(,)3k k 上有唯一一个零点, 同理13k k --<-,32(1)(1)0f k k k --=--+<,∴()f x 在(1,)3kk ---上有唯一一个零点,又()f x 在(,)33k k -上有唯一一个零点,∴()f x 有三个零点. 综上可知k 的取值范围为4(0,)27. 3.(2020·浙江省杭州第二中学高三三模)设函数11,(,2)(){1(2),[2,)2x x f x f x x --∈-∞=-∈+∞,则函数()()1F x xf x =-的零点的个数为( )A .4B .5C .6D .7【答案】C 【解析】,转化为如图,画出函数和的图像,当时,有一个交点, 当时,,,此时,是函数的一个零点, ,,满足,所以在有两个交点,同理,所以在有两个交点, ,所以在内没有交点,当时,恒有,所以两个函数没有交点,所以,共有6个.的图像在区间[1,1]-上有且仅有一个交点.在同一平面直角坐标系中画出函数11,01()221,10xx x g x x +⎧⎛⎫≤≤⎪ ⎪=⎨⎝⎭⎪--≤<⎩与2y x m =+在区间函数[1,1]-上的大致图象如下图所示:结合图象可知:当(0)1h =,即1m =时,两个函数的图象只有一个交点;当(1)(1),11(1)(1)2h g m h g <⎧⇒-≤<-⎨-≥-⎩时,两个函数的图象也只有一个交点,故所求实数m 的取值范围是1|112m m m ⎧⎫-≤<-=⎨⎬⎩⎭或.。


第9讲利用导数解决整数解及方程根的个数问题【典例例题】题型一:整数解问题之化为直线与曲线位置关系问题【例1】(2023·全国·高三专题练习)若关于x 的不等式()()1e 21xa x x ->-(其中1a ≥-),有且只有两个整数解,则实数a 的取值范围是()A .235,43e ⎛⎤- ⎥⎝⎦B .31,2e ⎛⎤- ⎥⎝⎦C .235,43e ⎛⎤-- ⎥⎝⎦D .235,2e 3e ⎛⎤-- ⎥⎝⎦【答案】D 【解析】【分析】根据给定不等式,构造函数(()e 21)x f x x =-和()(1)g x a x =-,作出函数图象,结合图象分析求解作答.【详解】由不等式()()1e 21xa x x ->-(1a ≥-),令(()e 21)x f x x =-,()(1)g x a x =-,(()e 21)x f x x '=+,当12x <-时,()0f x '<,当12x >-时,()0f x '>,即函数()f x 在1(,2-∞-上单调递减,在1(,)2-+∞上单调递增,()min 12f x f ⎛⎫=-= ⎪⎝⎭12x <时,恒有()0f x <,函数()(1)g x a x =-,1a ≥-表示恒过定点(1,0),斜率为a -的直线,在同一坐标系内作出函数()y f x =的图象和直线(1)y a x =-,如图,因不等式()()1e 21xa x x ->-(1a ≥-)有且只有两个整数解,观察图象知,-1和0是不等式()()g x f x >解集中的两个整数,于是得o −1)>o −1)o −2)≤o −2),即2>−3e3≤−5e2,解得2352e 3e a -<≤-,所以实数a 的取值范围是235(,]2e 3e--.故选:D 【点睛】关键点睛:涉及不等式整数解的个数问题,构造函数,分析函数的性质并画出图象,数形结合建立不等关系是解题的关键.【例2】(2023·四川·成都七中模拟预测(理))已知不等式e (3)20(1)+--<<x a x x a 恰有2个整数解,则a 的取值范围为()A .2324e 3e ≤<a B .2324e 3e<≤a C .324e 3≤<a D .324e 3<≤a 【答案】C 【解析】【分析】首先通过不等式分析,排除3x ≤-的可能性,对于3x >-,将不等式分离参数,得到()23e x x a x +<+,分析排除0a ≤的情况,然后令()()23e x x g x x +=+,利用导数分析其单调性,结合函数的正负值和零点,极值点分析,得到函数的大致图象,然后观察图象分析,将问题要求等价转化为()()01g ag a ⎧>⎪⎨≤⎪⎩,进而求解.【详解】当3x =-时,e (3)20(1)+--<<x a x x a 即为0320+-<,即10<,不成立;当3x <-时不等式等价于()321111·e e 13e 3e e x xx x x a x x -+⎛⎫>=->=>> ⎪++⎝⎭,由于1a <,故不成立;当3x >-时,不等式等价于()23e x x a x +<+,若0a ≤,则不等式对于任意的2x >-恒成立,满足不等式的整数有无穷多个,不符合题意;当0a >时,令()()2,(3)3e xx g x x x +=>-+,则()()22553e xx x g x x ++'=-+,在⎛- ⎝⎭上()0g x '>,∴()g x 单调递增,在∞⎫+⎪⎪⎝⎭上()0g x '<,∴()g x 单调递减,且在(3,2)--上()0g x <,在()2,-+∞上()0g x >,又∵在x 趋近于+∞时,()g x 趋近于0,∴()g x 在()3,-+∞上的图象如图所示:∵5212-+-<-,∴当3x >-时,不等式等价于()23e x x a x +<+有两个整数解,这两个整数解必然是1-和0,充分必要条件是()()01g a g a ⎧>⎪⎨≤⎪⎩,即2334ea a⎧>⎪⎪⎨⎪≤⎪⎩,∴324e 3≤<a ,故选:C 【点睛】分类讨论是解决这类问题的重要方法,利用导数研究单调性后要结合函数的零点和极值,极限值进行分析,然后利用数形结合思想找到题设要求的充分必要条件,是问题解决的关键步骤.【例3】(2022·辽宁·辽阳市第一高级中学高二期末)已知函数()()1ln f x kx x x =+-,若()0≤f x 有且只有两个整数解,则k 的取值范围是()A .ln 5ln 2,3010⎛⎤⎥⎝⎦B .ln 5ln 2,3010⎛⎫⎪⎝⎭C .ln 2ln 3,1012⎛⎤ ⎥⎝⎦D .ln 2ln 3,1012⎛⎫⎪⎝⎭【答案】C 【解析】【分析】将问题化为ln (1)x k x x+≤有且只有两个整数解,利用导数研究ln ()xg x x =的性质,并画出()g x 与(1)y k x =+的图象,判断它们交点横坐标的范围,列不等式组求k 的范围.【详解】由题设,()f x 定义域为(0,)+∞,则()0≤f x 可得ln (1)x k x x+≤,令ln ()x g x x=,则21ln ()xg x x -'=,所以0e x <<时()0g x '>,即()g x 递增,值域为(1,e-∞;e x >时()0g x '<,即()g x 递减,值域为1(0,e;而(1)y k x =+恒过(1,0)-,函数图象如下:要使ln (1)xk x x+≤有且只有两个整数解,则(1)y k x =+与()g x 必有两个交点,若交点的横坐标为12x x <,则121234x x <≤<≤<,所以ln 232ln 343ln 454k k k ⎧≤⎪⎪⎪≤⎨⎪⎪>⎪⎩,即ln 2ln 31012k <≤.故选:C 【点睛】关键点点睛:首先转化为ln (1)xk x x+≤有且只有两个整数解,导数研究函数性质,再应用数形结合法判断ln ()xg x x=、(1)y k x =+交点横坐标范围,即可求参数范围.【题型专练】1.(2022·福建·莆田二中高二期中)设函数()e x f x x ax a =-+,其中1a >,若存在唯一的整数0x ,使得()00f x <,则a 的取值范围是()A .(21,2e ⎤⎦B .33e 1,2⎛⎤⎥⎝⎦C .343e 4e ,23⎛⎤⎥⎝⎦D .323e 2e ,2⎛⎤⎝⎦【答案】D 【解析】【分析】根据给定条件,构造函数()e ,()x g x x h x ax a ==-,将问题转化为存在唯一的整数0x 使得00(,())x g x 在直线()h x ax a =-下方,再借助导数探讨求解作答.【详解】令()e ,()x g x x h x ax a ==-,1a >,显然直线()h x ax a =-恒过点(1,0)A ,则“存在唯一的整数0x ,使得()00f x <”等价于“存在唯一的整数0x 使得点00(,())x g x 在直线()h x ax a =-下方”,(1())e x x g x +'=,当1x <-时,()0g x '<,当1x >-时,()0g x '>,即()g x 在(,1)-∞-上递减,在(1,)-+∞上递增,则当1x =-时,min 1()(1)eg x g =-=-,当0x ≤时,1()[,0]e g x ∈-,而()(0)1h x h a ≤=-<-,即当0x ≤时,不存在整数0x 使得点00(,())x g x 在直线()h x ax a =-下方,当0x >时,过点(1,0)A 作函数()e x g x x =图象的切线,设切点为(,e ),0t P t t t >,则切线方程为:e (1)e ()t t y t t x t -=+-,而切线过点(1,0)A ,即有e (1)e (1)t t t t t -=+-,整理得:210t t --=,而0t >,解得1(1,2)2t =∈,因(1)e 0(1)g h =>=,又存在唯一整数0x 使得点00(,())x g x 在直线()h x ax a =-下方,则此整数必为2,即存在唯一整数2使得点(2,(2))g 在直线()h x ax a =-下方,因此有23(2)(2)2e (3)(3)3e 2g h a g h a <⎧<⎧⇔⎨⎨≥≥⎩⎩,解得323e 2e 2a <≤,所以a 的取值范围是323e(2e ,]2.故选:D 【点睛】思路点睛:解决过某点的函数f (x )的切线问题,先设出切点坐标00(,)x y ,求导并求出切线方程000()()y y f x x x '-=-,然后将给定点代入切线方程转化为方程根的问题求解.2.(2022·青海·海东市第一中学模拟预测(理))已知函数()2e 2xx f x a x =-+,若有且仅有两个正整数,使得()0f x <成立,则实数a 的取值范围是()A .211,3e e ⎡⎫⎪⎢⎣⎭B .3291,5e e ⎡⎫⎪⎢⎣⎭C .391,5e 3e ⎡⎫⎪⎢⎣⎭D .212,2e e ⎡⎫⎪⎢⎣⎭【答案】C 【解析】【分析】将()0f x <转化为2(2)ex x a x +<,再分别求导分析2()e x x g x =和()(2)h x a x =+的图象,再分别求得()()1,1g ,()()2,2g ,()()3,3g 到()20-,的斜率,分析临界情况即可【详解】由()0f x <且0x >,得2(2)ex xa x +<,设2()e x x g x =,()(2)h x a x =+,22()e xx x g x '-=,已知函数()g x 在(0,2)上单调递增,在(2,)+∞上单调递减,函数()(2)h x a x =+的图象过点(2,0)-,(1)11(2)3e g =--,2(2)12(2)e g =--,3(3)93(2)5eg =--,结合图象,因为329115e 3e e <<,所以3915e 3ea ≤<.故选:C3.(2022·全国·模拟预测(理))已知关于x 的不等式222ln 0ax x x x +->的解集中只有1个整数,则实数a 的取值范围是().A .[)2,ln 21--B .(]2,ln 21--C .1ln 21,ln 33--⎛⎤ ⎥⎝⎦D .1ln 21,ln 33--⎡⎫⎪⎢⎣⎭【答案】B 【解析】【分析】由题可得不等式()2ln 0f x ax x x =+->仅有1个整数解,利用数形结合可得()()1020f f ⎧>⎪⎨≤⎪⎩,即求.【详解】由题可知()0,x ∈+∞,所以不等式222ln 0ax x x x +->,即2ln 0ax x x +->只有一个整数解,令()2ln f x ax x x =+-,不等式()0f x >仅有1个整数解,令2y ax =+,()ln g x x x =,则函数()ln g x x x =图象上仅有1个横坐标为整数的点落在直线2y ax =+的下方,∵()1ln g x x '=+,由()1ln 0g x x '=+=,得1ex =,∴()g x 在10,e ⎛⎫ ⎪⎝⎭上单调递减,在1,e ∞⎛⎫+ ⎪⎝⎭上单调递增,因为直线2y ax =+恒过点()0,2,作出函数()ln g x x x =与直线2y ax =+的大致图象,由图象可知,这个点()1,0,可得()()1020f f ⎧>⎪⎨≤⎪⎩,即2ln 21a -<≤-.故选:B .【点睛】关键点点睛:本题的关键是把问题转化为函数()ln g x x x =与直线2y ax =+的的交点的位置问题,然后利用数形结合解决.4.(2022·辽宁·沈阳二中高二期末)设函数()e (21)x f x x ax a =--+,若不等式()0f x <恰有两个整数解,则a 的取值范围是______.【答案】2533e 2ea ≤<【解析】【分析】由题知()e (21)1x x a x -<-恰有两个整数解,构造函数()()()()e 211,xg x h a x x x -==-,利用导数研究函数的性质,作出函数的大致图象,利用数形结合即得.【详解】由()0f x <,可得()e (21)1xx a x -<-,令()()()()e 211,xg x h a x x x -==-,由题意知恰有两个整数,使()g x ()h x <成立,因为()()e 21xg x x '=+,由()0g x '=,可得12x =-,所以当12x <-时,()0g x '<,函数()g x 单调递减,当12x >-时,()0g x '>,函数()g x 单调递增,所以()12min12e 2g x g -⎛⎫=-=- ⎪⎝⎭,且()()()1201,13e ,25e g g g --=--=--=-,直线()()1h x a x =-恒过点()1,0,且斜率为a,结合图象可得()()()()()()001122h g h g h g ⎧>⎪->-⎨⎪-≤-⎩,即12123e 35e a a a --->-⎧⎪->-⎨⎪-≤-⎩,解得2533e 2ea ≤<,即a 的取值范围是2533e 2ea ≤<.故答案为;2533e 2ea ≤<.题型二:方程根的个数问题【例1】(2022·福建·漳州市第一外国语学校高二期中)设函数()ln f x x x =⋅,则关于x 的方程()0f x m -=的实数根的个数不可能为()A .4B .3C .2D .1【答案】A 【解析】【分析】利用导数确定函数()f x 的单调性,进而得出函数()f x 的图象,数形结合得出方程实数根的个数.【详解】()ln 1f x x '=+1()0e f x x '>⇒>,1()00ef x x '<⇒<<即函数()f x 在10,e ⎛⎫⎪⎝⎭上单调递减,在1,e ⎛⎫+∞ ⎪⎝⎭上单调递增当0x →时,()0f x →,1111ln e e ee f ⎛⎫==- ⎪⎝⎭,(1)0f =则函数()y f x =与y m =的图象如下图所示平移直线y m =可知,函数()y f x =与y m =的交点个数可能为0,1,2,3则关于x 的方程()0f x m -=的实数根的个数可能为0,1,2,3故选:A【例2】(2022·重庆巴蜀中学高三阶段练习多选)已知函数(),115ln ,1xx x f x x x x⎧<⎪⎪-=⎨⎪≥⎪⎩,下列选项正确的是()A .函数()f x 的单调减区间为(),1-∞、()e,+∞B .函数()f x 的值域为(),1-∞C .若关于x 的方程()()20f x a f x -=有3个不相等的实数根,则实数a 的取值范围是5,e ∞⎛⎫+ ⎪⎝⎭D .若关于x 的方程()()20f x a f x -=有5个不相等的实数根,则实数a 的取值范围是51,e ⎡⎫⎪⎢⎣⎭【答案】ACD 【解析】【分析】利用函数的单调性与导数之间的关系可判断A 选项;求出函数()f x 的值域,可判断B 选项;数形结合可判断CD 选项.【详解】对于A 选项,当1x <时,()1x f x x =-,则()()2101f x x '=-<-,当1≥x 时,()5ln x f x x =,则()()251ln x f x x-'=,由()0f x '<可得e x >,所以,函数()f x 的单调减区间为(),1-∞、()e,+∞,A 对;对于B 选项,当1x <时,()1111f x x =+<-,当1≥x 时,()()5ln 50e ex f x f x ≤=≤=,因此,函数()f x 的值域为5,e ⎛⎤-∞ ⎥⎝⎦,B 错;对于CD 选项,作出函数()f x 的图像如下图所示:若0a ≤,由()()20f x a f x -=可得()0f x =,则方程()0f x =只有两个不等的实根;若0a >,由()()20f x a f x -=可得()0f x =或()f x a =或()f x a =-,由图可知,方程()0f x =有2个不等的实根,方程()f x a =-只有一个实根,若关于x 的方程()()20f x a f x -=有3个不相等的实数根,则5ea >,C 对;若关于x 的方程()()20f x a f x -=有5个不相等的实数根,则51ea ≤<,D 对.故选:ACD.【例3】(2022·江西赣州·高二期中(文))已知函数()ln x f x x=,关于x 的不等式()()20f x tf x ->有且只有四个整数解,则实数t 的取值范围是()A .ln 5ln 2,52⎡⎫⎪⎢⎣⎭B .ln 6ln 5,65⎡⎫⎪⎢⎣⎭C .ln 6ln 5,65⎛⎤⎥⎝⎦D .ln 3ln 4,34⎛⎤⎥⎝⎦【答案】B 【解析】【分析】求导,利用导数的符号变化研究其单调性、极值,对t 分类讨论,分别利用一元二次不等式的解法,结合函数图象和不等式的整数解个数进行判定求解.【详解】由ln ()x f x x=得()f x '21ln xx -=,当0e x <<时,()0f x '>,()f x 单调递增;当e x >时,()'0f x <,()f x 单调递减;所以当e x =时,()f x 有最大值,且max 1()(e)ef x f ==,又当x →+∞时,()0f x →,且()0f x >,当0x →时,()f x →-∞,(1)0f =.其图象如图所示:①当0=t ,由()()20f x tf x ->,得()20f x >,即()0f x ≠,则1x ≠,此时不等式的整数解有无数多个,不合题意;②当0t <时,由()()20f x tf x ->得()0f x >或()f x t <.当()0f x >时,1x >,有无数个整数解;当()0f x t <<时,其解集为(0,1)的子集,不含有整数解;故0t <不合题意;③当0t >时,由()()20f x tf x ->得()f x t >或()0f x <,当()0f x <时,其解集为(0,1),不含有整数解;当()f x t >时,若不等式有且仅有四个整数解,又()ln333f =,()()ln2242f f ==,()ln555f =,()666ln f =,且()()()()()32456f f f f f >=>>,因为()f x 在()0,e 递增,在()e,+∞递减,所以四个整数解只能为2、3、4、5,所以()()65f t f ≤<,即n6n 65l l 5t ≤<所以实数t 的取值范围为ln6ln5[,65.故选:B.【例4】(2022·江西省宜春中学高二开学考试(理))已知函数2,1()ln 42,1xx f x e x x x x ⎧>⎪=⎨⎪--≤⎩,若函数[]2()(24)()1y f x a f x =+-+恰有5个零点,则实数a 的取值范围是()A .949,824⎡⎫⎪⎢⎣⎭B .491,24⎛⎫ ⎪⎝⎭C .91,5⎛⎫ ⎪⎝⎭D .91,5⎡⎤⎢⎥⎣⎦【答案】C 【解析】【分析】先研究1x >时,()ln xf x e x=的单调性和极值,然后画出分段函数的图象,再令()f x t =,通过换元后数形结合,可转化为一元二次方程根的分布问题,从而即可求解.【详解】解:当1x >时,()ln xf x e x=,则2ln 1()ln x f x e x -'=,当1x e <<时,()0f x '<,()f x 单调递减,当x e >时,()0f x '>,()f x 单调递增,所以1x >时,()()1f x f e =;当1x 时,22()52(1)55f x x x x =--=-++;作出()f x大致图象如下:由函数2[()](24)()1y f x a f x =+-+恰有5个不同零点,即方程2[()](24)()10f x a f x +-+=恰有5个不等实根,令()f x t =,则方程2(24)10(*)t a t +-+=,令函数2()(24)1u t t a t =+-+,①方程(*)在区间(,1)-∞和()1,5上各有一个实数根,则(1)12410(5)255(24)10u a u a =+-+<⎧⎨=+-+>⎩,解得915a <<;②方程(*)在区间()1,5和(5,)+∞各有一个实数根,则(1)12410(6)255(24)10u a u a =+-+>⎧⎨=+-+<⎩,不等式组无解;③方程(*)的两根为1和5,此时()1524151a ⎧+=--⎨⨯=⎩无解.综上,915a <<.故选:C.【题型专练】1.(2022·广西百色·高二期末(理))设函数()()ln ,0e 1,0x x xf x x x >⎧=⎨+≤⎩,若函数()y f x b =-有两个零点,则实数b 的取值范围是()A .()0,1B .[)0,1C .[]0,1D .[]{}20,1e-⋃-【答案】D 【解析】【分析】先求导得出()f x 的单调性,进而画出()f x 的图象,将题设转化为函数()y f x =与y b =有两个交点,结合图象求出实数b 的取值范围即可.【详解】当0x >时,函数()ln f x x =单调递增;当0x ≤时,()()e 1xf x x =+,则()()e 20x f x x ='+=时,2x =-,所以当2x <-时,()0f x '<,20x -<≤时,()0f x '>,故当0x ≤时,()f x 在(),2-∞-上单调递减,在()2,0-上单调递增,所以()f x 在2x =-处取极小值,极小值为()22e f --=-,作出函数()f x 的图象如图:因为函数()y f x b =-有两个零点,所以函数()y f x =与y b =有两个交点,所以当[]{}20,1e b -∈⋃-时函数()y f x =与y b =有两个交点,所以实数b 的取值范围为[]{}20,1e -⋃-.故选:D.2.(2022·宁夏中卫·一模(文))设函数()ln 0ex xx f x x x ⎧>=⎨≤⎩若函数()()g x f x m =-有两个零点,则实数m 的取值范围是()A .1,e e ⎛⎫- ⎪⎝⎭B .1,0e ⎛⎤- ⎥⎝⎦C .1,0(0,)e ⎛⎫-+∞ ⎪⎝⎭D .1,e ⎛⎫-+∞ ⎪⎝⎭【答案】D 【解析】【分析】()()g x f x m =-有两个零点等价于()y f x =与y m =的图象有两个交点,利用导数分析函数()e ,0xh x x x =≤的单调性与最值,画出函数()f x 图象,数形结合可得结果.【详解】解:设()e ,0x h x x x =≤,则()()'e 1xh x x =+,所以()h x 在(),1-∞-上递减,在(]1,0-上递增,()()min 11eh x g =-=-,且1x <-时,()0h x <,()()g x f x m =-有两个零点等价于()y f x =与y m =的图象有两个交点,画出()y f x =的图象,如下图所示,由图可得,1>em -时,()y f x =与y m =的图象有两个交点,此时,函数()()g x f x m =-有两个零点,∴实数m 的取值范围是1,e ⎛⎫-+∞ ⎪⎝⎭,故选:D.【点睛】方法点睛:本题主要考查分段函数的性质、利用导数研究函数的单调性、函数的零点,以及数形结合思想的应用,属于难题.数形结合是根据数量与图形之间的对应关系,通过数与形的相互转化来解决数学问题的一种重要思想方法,函数图象是函数的一种表达形式,它形象地揭示了函数的性质,为研究函数的数量关系提供了“形”的直观性.归纳起来,图象的应用常见的命题探究角度有:1、确定方程根的个数;2、求参数的取值范围;3、求不等式的解集;4、研究函数性质.3.(2022·新疆维吾尔自治区喀什第二中学高二期中(理))已知函数()34,0,0x x x f x lnx x ⎧-≤=⎨>⎩,若函数()()g x f x x a =+-有3个零点,则实数a 的取值范围是()A .[)0,1B .[)0,2C .(],1-∞D .(],2-∞【答案】B 【解析】【分析】构造()()x f x x ϕ=+,通过求导,研究函数的单调性及极值,最值,画出函数图象,数形结合求出实数a 的取值范围.【详解】令()()0g x f x x a =+-=,即()f x x a +=,令()()x f x x ϕ=+,当0x ≤时,()33x x x ϕ=-,()233x x ϕ'=-,令()0x ϕ'>得:1x >或1x <-,结合0x ≤,所以1x <-,令()0x ϕ'<得:11x -<<,结合0x ≤得:10-<≤x ,所以()x ϕ在1x =-处取得极大值,也是最大值,()()max 12x ϕϕ=-=,当x →-∞时,()x ϕ→-∞,且()00ϕ=,当0x >时,()ln x x x ϕ=+,则()110x xϕ'=+>恒成立,()ln x x x ϕ=+单调递增,且当0x →时,()x ϕ→-∞,当x →+∞时,()x ϕ→+∞,画出()x ϕ的图象,如下图:要想()()g x f x x a =+-有3个零点,则[)0,2a ∈故选:B。


运用导数如何展开对方程根的个数的讨论1 已知函数321()1()3f x x ax x a R =--+∈ (1)若函数()f x 在12,x x x x ==处取得极值,且122x x -=,求a 的值及()f x 的单调区间;(2)若12a <,讨论曲线()f x 与215()(21)(21)26g x x a x x =-++-≤≤的交点个数. 解:(1)2()21f'x x ax =--12122,1x x a x x ∴+=⋅=-122x x ∴-===0a ∴=…………………………………2分22()211f x x ax x '=--=-令()0f x '>得1,1x x <->或 令()0f x '<得11x -<<∴()f x 的单调递增区间为(,1)-∞-,(1,)+∞,单调递减区间为(1,1)-…………5分(2)由题()()f x g x =得3221151(21)326x ax x x a x --+=-++ 即32111()20326x a x ax -+++= 令32111()()2(21)326x x a x ax x ϕ=-+++-≤≤……………………6分 2()(21)2(2)(1)x x a x a x a x ϕ'∴=-++=--令()0x ϕ'=得2x a =或1x =……………………………………………7分12a <Q 当2a ≤-此时,9802a -->,0a <,有一个交点;…………………………9分当22a ≥-即11a -<<时,2(32)036a a -+>Q , ∴当9802a -->即9116a -<<-时,有一个交点; 当98002a a --≤≤,且即9016a -≤≤时,有两个交点; 当102a <<时,9802a --<,有一个交点.………………………13分 综上可知,当916a <-或102a <<时,有一个交点; 当9016a -≤≤时,有两个交点.…………………………………14分选天星试题调研压轴大题P69页选自刷题P49页选自刷题P43页。

导数--根的个数问题题型一:原函数根的个数问题第一步:画岀 “趋势图”,如画岀三次函数的大致趋势“是先增后减再增”还是“先减后增再减” 第二步:由趋势图结合交点个数或根的个数写不等式(组) ;主要看极大值和极小值与 0的关系;第三步:解不等式(组)即可; 例1、已知函数f(x) - x3-(k^x 2, g(x) - kx ,且f(x)在区间(2,)上为增函数. 32 3(1) 求实数k 的取值范围; (2) 若函数f (x)与g(x)的图象有三个不同的交点,求实数k 的取值范围.2解:(1 )由题意f (x) x(k 1)x - •- f (x)在区间(2,)上为增函数, ••• f (x) x 2 (k 1)x0在区间(2,)上恒成立(分离变量法)即k 1 x 恒成立,又x2,• k 1 2,故k 1 • k 的取值范围为k 1(2)设 h(x) f(x) g(x) — 坐 ©x2kx -, 3 2 3h(x)x 2 (k 1)x k(x k)(x 1)令 h (x) 0得x k 或x 1由( 1 )知 k 1,①当k 1时, h (x ) (x 1)2 0,h(x)在R 上递增,显然不合题意②当k 1时,h(x), h (x)随x 的变化情况如下表:k 1由于0,欲使f (x)与g(x)的图象有三个不同的交点,即方程 h(x) 0有三个不同的实根,故需 2k 3 k 2 12k 10,即(k 1)(k 2k 2) 02,解得 k 1 、3623k 2 2k 2 0综上,所求k的取值范围为k 1 再3 1 2例2、已知函数f(x) ax x 2x c2(1 )若x 1是f (x)的极值点且f (x)的图像过原点,求f (x)的极值;1 2(2)若g(x) bx x d,在(1 )的条件下,是否存在实数b,使得函数g(x)的图像与函数2像恒有含x 1的三个不同交点?若存在,求岀实数b的取值范围;否则说明理由。

利用导数讨论方程根的存在性及个数的一般方法摘要:函数的零点就是方程的根,也是曲线与x轴的交点的横坐标,所以函数的零点、方程的根、曲线与x轴的交点的横坐标之间是可以相互转化的。
有些函数较为复杂,无法直接求出函数的零点或者对应方程的根,此时我们就需要利用导数法,来讨论函数曲线与轴的交点情况.下面我们结合实例来探讨一下如何运用导数法讨论函数的零点或者方程的根的问题。
关键词:数形结合,函数的导数与函数图像,罗尔定理,根的存在性定理方程的(实)根,也称为函数的零点,它是曲线与轴交点的横坐标。
在讨论方程的根的存在性及个数的问题上,导数是一个很好的工具。
这一类问题上关键是将方程的问题转化成函数的零点或者函数图像交点问题,利用导数讨论函数的性质结合零点定理及函数图像来解决问题。
1.如何判别方程存在根?解题思路(1)利用连续函数的根值定理(零点定理)若题给出可导条件时,往往须先用导数的有关知识或中值定理,进而再用根值定理。
若满足根值定理的条件,则可判定方程在区间内至少存在一个根。
推广根值定理中的闭区间,可推广至开区间或无限区间,,。
这里以无限区间为例来说明:设在内连续若,,且与异号或若,则在内至少存在一个根。
(2)利用罗尔定理根据已给方程,做辅助函数,使,验证在上满足罗尔定理的条件。
则在上至少存在一个根。
用广义罗尔定理也可,这实际上是把罗尔定理中的区间,推广至无限区间。
例1设,求证:方程在区间与内各至少有一个实根。
解已知方程可改写作设因为在上连续,且 ,所以由根值定理,存在,使得,是方程的根。
同理可证,存在,使得,是方程的根。
1.如何判断方程实根的个数?解题思路1.用导数确定函数的增减区间及极值,考查曲线与轴交点的个数。
2.用二阶导数确定曲线是上凹(或下凹),以确定线与轴有两个交点(图1)。
图11.用罗尔定理估计方程根的个数:设在上连续,在可导若没有零点,则在内最多只有一个根。
若有一个(个)零点,则在内至多有两个个根。
