第七章 抽样与抽样分布

抽样与抽样分布在统计学中，抽样是一种常用的数据收集方法，通过从总体中选择一部分样本来进行研究和分析。

抽样的目的是通过样本来推断总体的特征和性质。

在进行抽样时，我们需要了解抽样的方法和抽样分布的概念。

一、抽样方法1. 无偏抽样无偏抽样是指所有样本有相同被选中的机会。

这样可以确保样本的代表性，从而减小样本估计值和总体真值之间的误差。

常见的无偏抽样方法包括简单随机抽样、系统抽样和分层抽样等。

2. 有偏抽样有偏抽样是指样本的选择并不具有相等的机会。

这样可能导致样本的代表性不足，从而产生较大的估计误差。

有时，有偏抽样也可以用于特定的研究目的，但需要明确地说明和分析偏差带来的影响。

二、抽样分布1. 抽样分布的概念抽样分布是指统计量在各个可能样本上的取值分布。

统计量可以是样本均值、样本方差等。

抽样分布的性质对于进行统计推断和假设检验非常重要。

2. 样本均值的抽样分布样本均值的抽样分布在中心极限定理的条件下近似服从正态分布。

中心极限定理指出，当样本容量足够大时，无论总体分布如何，样本均值的抽样分布都会接近正态分布。

3. 样本比例的抽样分布样本比例的抽样分布在满足一些条件的情况下也近似服从正态分布。

这些条件包括样本容量足够大、总体比例接近0.5以及样本与总体之间的独立性等。

4. 样本方差的抽样分布样本方差的抽样分布不服从正态分布。

通常情况下，样本方差的抽样分布呈右偏态，即偏度大于0。

为了得到样本方差的抽样分布，可以使用抽样分布的近似分布，如卡方分布。

三、应用案例抽样与抽样分布的方法和理论在实际统计学中有广泛的应用。

以下是一些常见的应用案例：1. 调查研究在进行调查研究时，我们经常需要从总体中选择一部分样本进行问卷调查或面访。

通过利用抽样与抽样分布的方法，我们可以将样本的调查结果推广到总体中，从而得到总体的特征和性质。

2. 假设检验假设检验是统计学中常用的推断方法之一。

通过比较样本统计量与假设的总体参数值，我们可以判断假设的合理性。

第七章整群抽样第一节整群抽样概述一、整群抽样的概念整群抽样是先将总体各单元划分成若干群（组），然后以群为单位，从中随机抽取一部分群，对中选群内的所有单元进行全面调查。

确切地说，这种抽样组织形式应称为单级整群抽样。

如果总体中的单元可以分成多级，则可以对前几级单元采用多阶抽样，而在最后一阶中对该阶抽样单元所包含的全部个体（最基本单元）进行调查，这种抽样称作多级整群抽样。

本章只讨论单级整群抽样。

设总体被划分为Ｎ群，第i群含有Ｍi个次级单元，全部总体次级抽样单元数记为Ｍ0，即Ｍ0＝∑M i。

当诸Ｍi都相等时，称为等群；否则，称为不等群。

采用整群抽样的两个理由：- 抽选群能大大降低数据收集的费用，当总体的分布比较广且调查采用面访时更是如此；- 从总体中直接抽选个体在实际中并不总是可行的（没有关于个体的抽样框）；有时，抽选单元组成群体组更简便易行（如整个住户）。

整群抽样包括两步：首先，总体被分为群；然后，在总体中抽取群的样本并访问群中的所有单元。

如果总体单元是自然分成组或群的，创建一个这种关于群的抽样框并对它们进行抽样比创建总体中所有单元的名录框更为容易。

或者，无法得到关于总体中所有单元的名录框，但却有这些单元分布地域的地图，因而可以创建地域框。

群的抽取可以采用简单随机抽样、系统抽样或PPS抽样等各种不同的方法。

二、群的划分问题整群抽样策略的统计效率取决于群内单元的相似程度有多大，每个群中有多少单元，及抽中群的数量。

同分层抽样一样，整群抽样的前提是先要对总体进行分群。

关于群的划分，有两个问题：一是如何定义群，即当群并非是一个自然形成的单位时，确定每个群的组成；二是如何确定群的规模即群的大小。

分层抽样是在各层都进行随机抽样，“层是缩小了的总体”，抽样单元仍然是总体基本单元。

这决定了分层的原则是：尽量缩小层内差异，而扩大层间差异。

而整群抽样只是在各群之间抽取一部分群进行调查，并在抽中的群内作全面调查。

因此，群间差异的大小直接影响到抽样误差的大小，而群内差异的大小则不影响抽样误差。

（标准抽样检验）第七章整群抽样第七章整群抽样第一节整群抽样概述一、整群抽样的概念整群抽样是先将总体各单元划分成若干群（组），然后以群为单位，从中随机抽取一部分群，对中选群内的所有单元进行全面调查。

确切地说，这种抽样组织形式应称为单级整群抽样。

如果总体中的单元可以分成多级，则可以对前几级单元采用多阶抽样，而在最后一阶中对该阶抽样单元所包含的全部个体（最基本单元）进行调查，这种抽样称作多级整群抽样。

本章只讨论单级整群抽样。

设总体被划分为Ｎ群，第i群含有Ｍi个次级单元，全部总体次级抽样单元数记为Ｍ0，即Ｍ0＝∑M i。

当诸Ｍi都相等时，称为等群；否则，称为不等群。

采用整群抽样的两个理由：-抽选群能大大降低数据收集的费用，当总体的分布比较广且调查采用面访时更是如此；-从总体中直接抽选个体在实际中并不总是可行的（没有关于个体的抽样框）；有时，抽选单元组成群体组更简便易行（如整个住户）。

整群抽样包括两步：首先，总体被分为群；然后，在总体中抽取群的样本并访问群中的所有单元。

如果总体单元是自然分成组或群的，创建一个这种关于群的抽样框并对它们进行抽样比创建总体中所有单元的名录框更为容易。

或者，无法得到关于总体中所有单元的名录框，但却有这些单元分布地域的地图，因而可以创建地域框。

群的抽取可以采用简单随机抽样、系统抽样或PPS抽样等各种不同的方法。

二、群的划分问题整群抽样策略的统计效率取决于群内单元的相似程度有多大，每个群中有多少单元，及抽中群的数量。

同分层抽样一样，整群抽样的前提是先要对总体进行分群。

关于群的划分，有两个问题：一是如何定义群，即当群并非是一个自然形成的单位时，确定每个群的组成；二是如何确定群的规模即群的大小。

分层抽样是在各层都进行随机抽样，“层是缩小了的总体”，抽样单元仍然是总体基本单元。

这决定了分层的原则是：尽量缩小层内差异，而扩大层间差异。

而整群抽样只是在各群之间抽取一部分群进行调查，并在抽中的群内作全面调查。

（抽样检验）第七章第⼀次课抽样原理与⽅法第⼀节抽样⽅案的制定在科学研究中，除了进⾏控制试验外，有时也要进⾏调查研究。

调查研究是对已有的事实通过各种⽅式进⾏了解，然后⽤统计的⽅法对所得数据进⾏分析，从⽽找出其中的规律性。

例如，了解畜禽品种及⽔产资源状况；探索和分析对某种疾病有效的防治规律、措施以及新的检验⼿段和⽅法等。

由于现场调查⽴⾜于⽣产实际，所以它是研究和解决实际问题的⼀种重要研究⽅法。

同时，控制试验的研究课题，往往是在调查研究的基础上确定的；试验研究的成果，⼜必须在其推⼴应⽤后经调查得以验证。

为了使调查研究⼯作有⽬的、有计划、有步骤地顺利开展，必须事先拟定⼀个详细的调查计划。

调查计划应包括以下⼏个内容：(⼀) 调查研究的⽬的任何⼀项调查研究都要有明确的⽬的，即通过调查了解什么问题，解决什么问题。

例如，家畜健康状况的调查的⽬的是评定家畜健康⽔平；畜禽品种资源调查的⽬的是了解畜禽品种的数量、分布与品种特征特性等情况。

同时，调查研究的⽬的还应该突出重点，⼀次调查应针对主要问题收集必要的数据，深⼊分析，为主要问题的解决提出相应的措施和办法。

(⼆) 调查的对象与范围根据调查的⽬的，确定调查的对象、地区和范围，划清调查总体的同质范围、时间范围和地区范围。

例如，四川省家禽品种资源调查，调查地区为四川省，调查总体和对象为全省各市、县的家禽，调查时间从2000年1⽉到2000年12⽉。

(三) 调查的项⽬调查项⽬的确定要紧紧围绕调查⽬的。

调查项⽬确定的正确与否直接关系到调查的质量。

因此，项⽬应尽量齐全，重要的项⽬不能漏掉；项⽬内容要具体、明确，不能模棱两可。

应按不同的指标顺序以表格形式列⽰出来，以达到顺利完成搜集资料的⽬的。

例如，家禽品种资源调查项⽬有：种类(鸡、鸭、鹅等)、品种(柴鸡、来航、⽩洛克等)，数量、体重、产蛋性能等项⽬。

调查项⽬有⼀般项⽬和重点项⽬之分。

⼀般项⽬主要是指调查对象的⼀般情况，⽤于区分和查找，如畜主姓名、住址及编号等。

第七章 抽样调查一、本章重点1.抽样调查也叫做抽样推断或参数估计，必须坚持随机抽样的原则。

它是一种非全面调查，其意义在于对总体的推断上，存在可控制性误差。

是一种灵活快捷的调查方式。

2.抽样调查有全及总体与样本总体之区分。

样本容量小于30时一般称为小样本。

对于抽样调查来讲全及总体的指标叫做母体参数，是唯一确定的未知的量，样本指标是根据样本总体各单位标志值计算的综合性指标，是样本的一个函数，是一个随机变量，抽样调查就是要用样本指标去估计相应的总体指标。

样本可能数目与样本容量有关也与抽样的方法有关。

抽样方法可以分为考虑顺序的抽样与不考虑顺序的抽样；重复抽样与不重复抽样。

3.大数定律、正态分布理论、中心极限定理是抽样调查的数理基础。

正态分布的密度函数有两个重要的参数（σ;x ）。

它有对称性、非负性等特点。

中心极限定理证明了所有样本指标的平均数等于总体指标如X x E =)(。

推出了样本分布的标准差为：1--=N n N n x σμ。

4.抽样推断在逻辑上使用的是归纳推理的方法、在方法上使用的是概率估计的方法、存在着一定误差。

无偏性、一致性和有效性是抽样估计的优良标准。

抽样调查既有登记性误差，也有代表性误差，抽样误差是一个随机变量，而抽样的平均误差是一个确定的值。

抽样误差受总体标志值的差异程度、样本容量、抽样方法、抽样组织形式的影响。

在重复抽样下抽样的平均误差与总体标志值的差异程度成正比，与样本容量的平方根成反比即n x σμ=，不重复抽样的抽样平均误差仅与重复抽样的平均误差相差一个修正因子即N nn x -=1σμ。

在通常情况下总体的方差是未知的，一般要用样本的方差来代替。

把抽样调查中允许的误差范围称作抽样的极限误差x ∆或p ∆。

μt =∆，用抽样的平均误差来度量抽样的极限误差。

把抽样估计的把握程度称为抽样估计的置信度。

抽样的极限误差越大，抽样估计的置信度也越大。

抽样估计又可区分为点估计和区间估计。

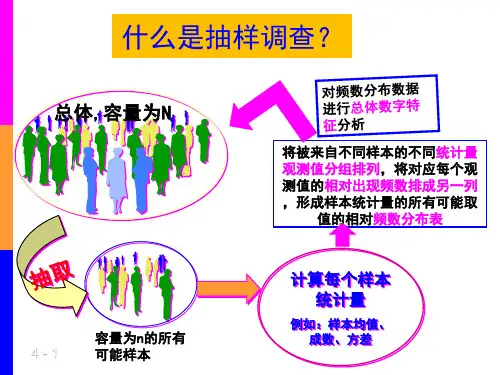
抽样与抽样分布抽样是统计学中一种重要的数据收集方法，通过从总体中选择一部分样本来代表整体，可以更方便、更经济地进行数据分析和推断。

而抽样分布则是与抽样密切相关的概念，指的是样本统计量的概率分布。

本文将从抽样的定义和目的、抽样方法和抽样分布的性质等方面进行探讨。

一、抽样的定义和目的抽样是统计学中利用一定的方法和技术从总体中选取一部分个体作为样本，以了解总体特征或者对总体进行推断的过程。

抽样的目的在于通过对样本的观测和研究来推断总体的特征，而无需对整个总体进行调查。

抽样可以减少调查或实验的成本、节约时间，并且在一定程度上能够保证结果的可靠性和精确度。

二、抽样方法1. 简单随机抽样：简单随机抽样是指从总体中随机选择样本，使每一个样本都有相同的概率被选中。

简单随机抽样通常需要使用随机数表、随机数发生器或者抽签等方法来实现。

2. 系统抽样：系统抽样是按照一定的规则和系统性地从总体中选择样本，例如每隔一个固定的间隔选取一个样本。

系统抽样的优点在于操作简单，但是如果总体中存在某种周期性或者规律性的分布，可能会导致抽样结果的偏差。

3. 整群抽样：整群抽样是将总体根据某些特征进行分类，然后从每个分类中随机选择一定数量的群体作为样本。

整群抽样适用于总体中存在明显的群体结构的情况，可以提高样本的代表性。

4. 分层抽样：分层抽样是按照某种特征将总体分为若干层，然后从每一层中随机选择一定数量的样本。

分层抽样可以更好地体现总体的结构和差异，提高样本的代表性和准确性。

三、抽样分布的性质抽样分布是样本统计量的概率分布，其具有以下几个重要性质：1. 无偏性：如果样本统计量的期望值等于总体参数的真值，那么称该统计量是无偏的。

即样本统计量是对总体参数的无偏估计。

无偏性是抽样分布的重要性质，保证了样本统计量的可靠性和准确性。

2. 一致性：当样本数量趋向无穷大时，样本统计量的值趋向于总体参数的真值。

即样本统计量在大样本情况下能够接近总体参数，具有一致性。