下载文档原格式
铰链的种类-铰链分类内容来源网络，由“深圳机械展（11万㎡，1100多家展商，超10万观众）”收集整理！更多cnc加工中心、车铣磨钻床、线切割、数控刀具工具、工业机器人、非标自动化、数字化无人工厂、精密测量、3D打印、激光切割、钣金冲压折弯、精密零件加工等展示，就在深圳机械展.铰链又称合页是用来连接两个固体并允许两者之间做相对转动的机械装置。
铰链可由可移动的组件构成，或者由可折叠的材料构成。
合页主要安装于门窗上,而铰链更多安装于柜体家具上，按材质分类主要分为，不锈钢铰链和铁铰链；为让人们得到更好的享受又出现了液压铰链（阻尼铰链），其特点是在柜门关闭时带来缓冲功能，最大程度的减小了柜门关闭时与柜体碰撞发出的噪音。
铰链种类与用途介绍1、直弯铰链门板盖住柜体18mm厚侧板的全部（即门板盖住侧板17mm），所用的铰链就是直弯铰链。
（1）铰链孔距默认110mm；（2）装铰链的侧板内空深度要大于70mm；（3）直弯铰链最大只能盖侧板17mm，所以25mm、35mm厚度的侧板门板全盖最大也只能盖住17mm。
2、中弯铰链门板盖住柜体18mm厚侧板的一半（即门板盖住侧板8mm），所用的铰链就是中弯铰链。
（1）铰链孔距边默认110mm；（2）装铰链的侧板内空深度要大于70mm；（3）中弯铰链最大只能盖侧板8mm。
3、大弯铰链门板完全不盖住柜体的侧板（即门板盖住侧板0mm），所用的铰链就是大弯铰链。
（1）铰链孔距边默认110mm；（2）装铰链的侧板内空深度要大于70mm；（3）大弯铰链相对于侧板是内嵌效果的，适用于各种厚度的侧板。
4、165°直弯铰链165°直弯铰链与普通的直弯铰链工艺是一样的，只是门板打开角度不一样，普通直弯铰链门板打开的角度为90°，165°的直弯铰链门板打开的角度是165°。
（1）铰链孔距边默认110mm；（2）装铰链的侧板内空深度要大于70mm；（3）165°直弯铰链最大只能盖侧板17mm，所以25mm、35mm厚度的侧板门板座全盖，最大也只能盖住17mm；（4）常用于转角柜门板。
第二章柔性铰链的分类与分析2.2柔性铰链的分类与分析柔性铰链是利用材料的变形产生位移的一种特殊运动副，用于提供绕轴作复杂运动的有限角位移，具有无机械摩擦、无间隙、易维护、分辨率高和可一体化加工等优点。
柔性铰链有很多种结构，最普通的形式是绕一个轴弹性弯曲，而且这种弹性变形是可逆的。
[现代精密机械设计]，如图2.1所示。
图2.1 柔性铰链结构简图Fig.2.1Diagram of flexure hinge2.2.1柔性铰链的分类及编号自20世纪60年代以来，国内外学者、科研院校及研究机构对柔性铰链进行了多方面的研究，包括理论计算、结构创新设计及应用等方面。
按目前国内外的发展研究状况，柔性铰链按其切口形状可分为单边的和双边的，按其截面曲线分为单一的和混合的；按运动副分可分为转动副、移动副和球副，按其传递运动和能量的方向分单轴柔性铰链、双轴柔性铰链、万向柔性铰链和柔性联杆。
按照横截面的不同形状，可以分为：矩形截面柔性铰链和圆形截面柔性铰链。
按研究出现的先后顺序可分为传统的柔性铰链和典型的大变形柔性铰链。
还有其他特殊类型的如弓形柔性铰链、三角形柔性铰链、叶状形的柔性铰链、簧片式的柔性铰链等等。
根据以上的分析可将柔性铰链分成以下三大类，如表2-1,2-2,2-3所示。
表2-1基本曲线规则截面单轴柔性铰链（）Single-Axis Flexure Hinges单轴对S-CCircular Flexure Hinge）直圆型（称1）抛物线型（Parabolic Flexure Hinge Inverse Parabolic Flexure反转抛物线（S-Ip）Hinge S-SSecant Flexure Hinge正割型（）hyperbolic cosine Flexure双曲余弦型（S-H）HingeS-Aarched Flexure Hinge）弓型（S-V型（V Flexure Hinge）VS-Cy）cycloidal Flexure Hinge摆线型（s-E ）椭圆型（Elliptical Flexure Hinge1单s-P ）Parabolic Flexure Hinge抛物线型（轴不hyperbolic cosine Flexure 双曲线型（对s-HcHinge）称s-CB导角型Corner-Filleted Flexure Hinge（）表2-2由基本柔性铰链混合而成的单轴铰链模型（）Single-Axis Flexure HingesS-BB 类型二2交错铰链直两个车轮铰链Cross（梁-混合cartwheel（FlexureS-BB直3flexural）Hinge梁hinges）混合型S-BB 类型三4交错叶片混合一二S-BB cross-axis flexural（5混合）pivot直梁-直圆导角型（Corner-Filleted S-CB）Flexure Hinge混合型直圆-导角S-CCB混合型直圆-椭圆S-CE1混合型表2-3双轴柔性铰链（Two-Axis Flexure Hinges）ted(serially-disposed) T-EE-NC-P两轴平行双11）notches轴柔性T-CC-C -V两轴垂直铰链并联-同位配置（collocatednotches）T-BB-C-P两轴平行例T-EE-V双轴椭圆铰链11子表2-4多轴柔性铰链（Multiple-Axis Flexure Hinges）Corner-Filleted导角型（M-CBFlexure Hinge）直圆型（Circular Flexure M-C抛物线型（Parabolic M-PFlexure Hinge）双曲线型（Hyperbolic M-H）Flexure Hinge编号规则：1、大写代表单轴对称，即双边切口，小写代表单轴不对称，即单边切口。
第一章绪论1.1 柔性铰链简介1.1.1 柔性铰链定义柔性铰链作为一种小体积、无机械摩擦、无间隙和运动灵敏度高的传动结构，被广泛应用于各种要求微小线位移或角位移、且高精度定位的场合。
开创了工作台进入毫米级的新时代。
柔性铰链有成千上万的应用，如：陀螺仪、加速度计、天平、控制导弹的喷嘴、控制器显示仪、记录仪、调整器、放大连杆、计算机、继电器和传动连杆。
60年代前后，由于宇航和航空等技术发展的需要，对实现小范围内偏转的支承，不仅提出了高分辨率的要求，而且对其尺寸和体积提出了微型化的要求。
人们在经过对各种类型的弹性支承实验探索后才逐步开发出体积小、无机械摩擦、无间隙的柔性铰链。
随后柔性铰链在支撑结构、联接结构、调整机构和测量仪器中的得到广泛应用,并获得了前所未有的高精度和稳定性，并日益成熟。
70年代末，美国国家标准局引入了柔性铰链机构以放大压电驱动器的位移，使其设计的工作台既具有亚纳米级的位移分辨率，又具有相对较大的行程。
近年来，柔性铰链以其特殊的性能在精密机械、精密测量、微米技术和纳米技术等领域得到广泛应用没，尤其是柔性铰链与压电致动结合实现超精密位移和定位。
柔性铰链用于绕轴作复杂的有限角位移，它的特点是：无机械摩擦、无间隙、运动灵敏度高。
柔性铰链有很多种结构，最普通的形式是绕一个轴弹性弯曲，这种弹性变形是可逆的。
1.1.2 柔性铰链运动的实现方法柔性铰链是通过弹性形变来实现铰链运动。
施加的弹性变形力会导致铰链中心点偏移其几何中心，从而影响柔性铰链的转动精度。
柔性铰链用于绕轴做复杂运动的有限角位移，它有很多种结构，最普通的形式是绕一个轴弹性弯曲，这种弹性变形是可逆的。
1.1.3 柔性铰链类型柔性铰链可分为单轴柔性铰链和双轴柔性铰链。
单轴柔性铰链的截面形状有圆形与矩形两种，如图1-1所示。
图1—1 单轴柔性铰链双轴柔性铰链是由两个互成90度的单轴柔性铰链组成的（如图1-2（a）），对于大部分应用，这种设计的缺点是两轴没有交叉，具有交叉的最简单的双轴柔性铰链是把颈部作成圆杆状（如图1-2（b）），这种设计简单且容易加工，但它的截面积比较小，因此纵向强度比图1-2（a）弱得多。
管状柔性铰链的有限元分析基于薄壁圆筒的单开口管状柔性铰链是一种新型的柔性铰链，其优点是内部可设置钢丝等传动机构，用途更为广泛。
应用有限元软件对管状柔性铰链在受力作用下的形变和应力状态进行研究，得出受力和形变具有非线性关系特征。
标签：管状柔性铰链；有限元；非线性关系1 概述典型的柔性铰链机构是通过对实体梁进行切削加工，形成不同形状开口的弹性部位作为柔性铰链，根据柔性铰链的开口形状可分为直梁型、圆角形、抛物线形和双曲线型等[1]。
其中直圆形柔性铰链如图1（a）所示。
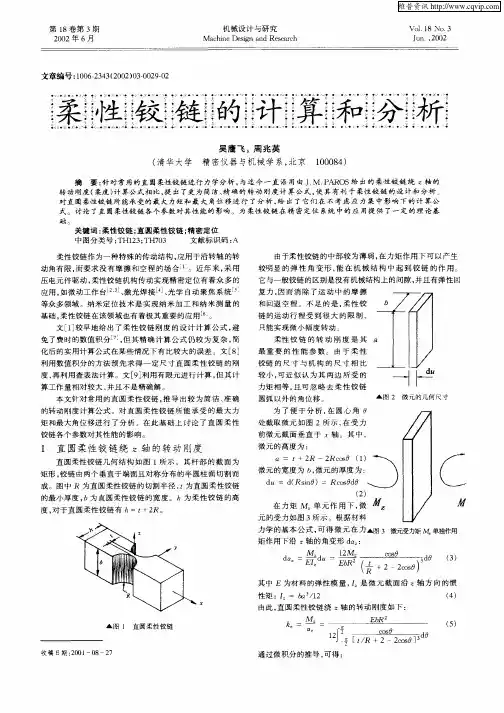
文章提出一种新的柔性铰链形式，通过对薄壁管进行切削加工，形成圆弧切口，在外力作用时该结构产生可逆的弹性形变，由此具备弹性铰链的特性，称之为管状柔性铰链，如图1（b）所示。
较之于传统柔性铰链，其最大特点是铰链的连接部分是管状构件，可以在内部布置一些传动系统，比如：钢丝等。
此结构不仅具有一般柔性铰链的特点并且这种柔性铰链比一般铰链具有更大的工程应用范围。
（a）（b）图1 传统柔性铰链和管状柔性铰链2 管状柔性铰链模型仿照典型的直圆形柔性铰链[2]，利用UGNX6.0[3]建模软件建立了圆形开口管状柔性铰链模型，其外形尺寸如图2所示。
机构全长l=100mm，内径r=10mm，壁厚d=1mm，中心圆形开口直径R=10mm，圆心距底边垂直距离s=2.5mm。
圆形开口柔性铰链是最简单的柔性铰链，在以后的研究中，还可以做椭圆形、抛物线形或直角形等其他开口形式的柔性铰链。
图2 圆形开口管状柔性铰链尺寸3 研究方法及结果3.1 ANSYS模型建立和加载计算方法依据上述模型尺寸在ANSYS14.0软件中建立片体模型，由于机构对称，可建立1/2模型，如图3（a）所示。
由于机构内径远大于壁厚，采用壳单元对机构进行模拟，假设机构为薄壁圆筒，选择SHELL181单元。
SHELL181适用于薄到中等厚度的壳结构，具有应力刚化及大变形功能，该单元有强大的非线性功能，并有截面数据定义、分析、可视化等功能。
铰链的基础知识铰链是一种常见的机械连接件，常用于门窗、家具以及其他工业制品中。
它具有使两个物体能够相对旋转的功能，同时还能够保持物体的稳定性和连接性。
本文将介绍铰链的基础知识，包括铰链的分类、结构、工作原理以及应用领域。
一、铰链的分类根据铰链的用途和结构，可以将铰链分为多种类型。
常见的铰链类型有以下几种：1. 钢铰链：由金属材料制成，具有较高的强度和耐用性，适用于较大的门窗和家具。
2. 塑料铰链：由塑料材料制成，具有轻便、防腐蚀的特点，适用于轻负荷的门窗和家具。
3. 隐形铰链：可以将门板和门框完全隐藏，使门面更加美观，适用于高要求的门窗装饰。
4. 轴承铰链：内部安装了轴承，能够承受较大的载荷，适用于重负荷的门窗和工业设备。
5. 双向铰链：可以使门窗可以同时向内和向外开启，方便使用和通风。
二、铰链的结构铰链主要由两个连接件组成：铰链螺钉和铰链杆。
铰链螺钉是连接在门板或门框上的一种固定件，通常由金属材料制成，具有较高的强度。
铰链杆是连接在门板或门框上的一种活动件，通常由金属材料制成，具有一定的弹性和可调节性。
三、铰链的工作原理铰链的工作原理基于杠杆原理和力的平衡。
当门板或门框受到外力作用时，铰链会产生一个反作用力，使门板或门框保持平衡。
同时，铰链的活动部分可以使门板或门框相对旋转，实现开启和关闭的功能。
四、铰链的应用领域铰链广泛应用于门窗、家具以及其他工业制品中。
在门窗中，铰链可以使门窗实现开启和关闭的功能，同时还能够保持门窗的稳定性和密封性。
在家具中，铰链可以使家具的抽屉、门板等部件实现开启和关闭的功能，方便使用和存放物品。
在工业制品中，铰链可以连接各种部件，实现相对旋转和调节的功能。
总结：铰链作为一种常见的机械连接件，具有使两个物体相对旋转的功能，同时还能够保持物体的稳定性和连接性。
根据用途和结构的不同，铰链可以分为多种类型。
铰链的结构主要由铰链螺钉和铰链杆组成，其工作原理基于杠杆原理和力的平衡。
曲梁柔性铰链性能分析及应用机构设计陈应舒;朱淳逸【摘要】基于线弹性和小变形以及欧拉伯努利梁理论,对圆弧曲梁柔性铰链的柔度以及精度进行了分析,得到了柔度与精度公式.使用ANSYS对柔度公式进行了验证.该公式在细长曲梁的情况之下有足够的精确性.设计了一种基于圆弧曲梁柔性铰链的多环平行导向机构,并对此机构分别在水平作用和竖直作用下的平行导向性能进行了有限元分析,有限元结果表明:此机构能够满足对水平方向和竖直方向上的导向功能.为柔性铰链的研究以及柔顺机构的设计均提供了一定的参考和借鉴.【期刊名称】《机械设计与制造》【年(卷),期】2018(000)011【总页数】4页(P183-185,189)【关键词】曲梁;柔性铰链;柔度;机构设计【作者】陈应舒;朱淳逸【作者单位】陕西理工大学机械工程学院,陕西汉中 723000;陕西理工大学机械工程学院,陕西汉中 723000【正文语种】中文【中图分类】TH161 引言柔性铰链是柔顺机构中重要的组成部分。
随着柔顺机构的在微精密机械、光学、医学等领域的快速普及使得对柔性铰链的研究逐渐引起了国内外众多研究人员的重视。
近十几年来人们对柔性铰链的研究逐渐细化，各种形状各异的柔性铰链被提出与研究。
目前，对直梁型柔性铰链的研究最为透彻，不论是文献[1]所提到的深切口椭圆柔性铰链，文献[2]中的圆弧形柔性球铰，还是文献[3]中所提及的单边型柔性铰链。
从本质来看，这些均为等截面或变截面的直梁。
国内外文献对于直梁柔性铰链的分析研究方法也已经相当完备。
对直梁柔性铰链的应用也是做了大量研究，如文献[4]设计了一种基于柔性铰链的微位移放大机构；文献[5]设计并分析了一种三自由度的精密定位平台等等。
考虑到设计要求与工作场合等实际情况，单纯使用直梁柔性铰链作为铰链单元所组成的柔顺机构可能并不能满足某些工作需要。
而曲梁柔性铰链是柔性铰链作为梁弯曲的中性面在自然状态之下呈现曲面的一类柔性铰链，能够为丰富柔顺机构的设计思路，对柔顺机构的设计提供一些构型上的补充。
2.2柔性铰链的分类与分析柔性铰链是利用材料的变形产生位移的一种特殊运动副，用于提供绕轴作复杂运动的有限角位移，具有无机械摩擦、无间隙、易维护、分辨率高和可一体化加工等优点。
柔性铰链有很多种结构，最普通的形式是绕一个轴弹性弯曲，而且这种弹性变形是可逆的。
[现代精密机械设计]，如图2.1所示。
图2.1 柔性铰链结构简图Fig.2.1Diagram of flexure hinge2.2.1柔性铰链的分类及编号自20世纪60年代以来，国内外学者、科研院校及研究机构对柔性铰链进行了多方面的研究，包括理论计算、结构创新设计及应用等方面。
按目前国内外的发展研究状况，柔性铰链按其切口形状可分为单边的和双边的，按其截面曲线分为单一的和混合的；按运动副分可分为转动副、移动副和球副，按其传递运动和能量的方向分单轴柔性铰链、双轴柔性铰链、万向柔性铰链和柔性联杆。
按照横截面的不同形状，可以分为：矩形截面柔性铰链和圆形截面柔性铰链。
按研究出现的先后顺序可分为传统的柔性铰链和典型的大变形柔性铰链。
还有其他特殊类型的如弓形柔性铰链、三角形柔性铰链、叶状形的柔性铰链、簧片式的柔性铰链等等。
根据以上的分析可将柔性铰链分成以下三大类，如表2-1,2-2,2-3所示。
表2-1基本曲线规则截面单轴柔性铰链（Single-Axis Flexure Hinges）铰链名称铰链模型分类编号单轴对称直梁型（Constant RectangularCross-Section Flexure Hinge）S-R 直圆型（Circular Flexure Hinge）S-C椭圆型（EllipticalFlexure Hinge）浅切口椭圆S-E1深切口椭圆S-E2双曲线型（Hyperbolic Flexure Hinge）S-H 抛物线型（Parabolic Flexure Hinge）S-P反转抛物线（Inverse Parabolic FlexureHinge）S-Ip 正割型（Secant Flexure Hinge）S-S双曲余弦型（hyperbolic cosine FlexureHinge）S-H 弓型（arched Flexure Hinge）S-A V型（V Flexure Hinge）S-V 摆线型（cycloidal Flexure Hinge）S-Cy单轴不对称椭圆型（Elliptical Flexure Hinge）s-E1抛物线型（Parabolic Flexure Hinge）s-P双曲线型（hyperbolic cosine FlexureHinge）s-Hc 导角型（Corner-Filleted Flexure Hinge）s-CB混合型s-CCB表2-2由基本柔性铰链混合而成的单轴铰链模型（Single-Axis Flexure Hinges）组合方式产生对象铰链模型分类编号直梁-直梁混合型两个混合交错铰链（CrossFlexureHinge）类型一S-BB1类型二S-BB2车轮铰链（cartwheelflexuralhinges）S-BB3类型三S-BB4一二混合交错叶片混合（cross-axis flexuralpivot）S-BB5直梁-直圆混合型导角型（Corner-FilletedFlexure Hinge）S-CB直圆-导角混合型S-CCB直圆-椭圆混合型S-CE1表2-3双轴柔性铰链（Two-Axis Flexure Hinges）铰链名称铰链模型分类编号双轴柔性铰链串联-非同位配置（non-collocated(serially-disposed)notches）两轴垂直T-CE1-NC-V两轴平行T-E1E1-NC-P并联-同位配置（collocatednotches）两轴垂直T-CC-C -V两轴平行T-BB-C-P例子双轴椭圆铰链T-E1E1-V表2-4多轴柔性铰链（Multiple-Axis Flexure Hinges）铰链名称铰链模型分类编号圆柱型（cylindrical）M-Cyl导角型（Corner-FilletedFlexure Hinge）M-CB直圆型（Circular FlexureHinge）M-C椭圆型（Elliptical FlexureM-EHinge）抛物线型（ParabolicM-P Flexure Hinge）双曲线型（HyperbolicM-H Flexure Hinge）编号规则：1、大写代表单轴对称，即双边切口，小写代表单轴不对称，即单边切口。
例S-代表单轴双切口、s-代表单轴单切口。
2、第一个字母代表自由度的个数，及S-、T-、M-分别代表单轴、双轴和多轴。
3、第二个字母代表切口类型，混合型的为两个同类型的字母组合。
4、在双轴铰链中，最后一个字母代表组合后两铰链轴线的相对位置。
V-代表垂直，P-代表平行。
第三个字母NC-代表非同位配置，C-代表同位配置。
2.2.2柔性铰链的计算与分析关于柔性铰链的设计研究，柔性铰链刚度的理论研究大都停留在单轴柔性铰链的范围内，有关单轴柔性铰链分析建模的研究主要包括弹性梁理论、卡氏第二定理、逆保角映射理论和有限元分析方法等，工程实践中一般采用数值积分法和有限元分析方法。
柔性铰链设计时基本参数应满足如下要求：[现代精密机械设计]1、柔性铰链内部应力要小于材料的许用应力。
在微位移范围内，此条件一般都能满足。
2、微位移器产生的最大位移输出时，微动台的弹性恢复力应小于微位移器的最大驱动力。
3、微动台的刚性应尽可能大，使其具有良好的动态特性和抗干扰能力。
2.2.2.1 几种常见柔性铰链的设计计算对于单轴柔性铰链，设计要求为对输入或灵敏轴必须灵活，一般绕横轴和沿纵轴铰链的刚度应尽可能的好[现代精密机械设计]。
也就是说单轴柔性铰链绕Z轴方向的转角刚度要尽可能的小、绕X轴方向的转角刚度和沿Y轴方向的轴向刚度要尽可能的大，坐标轴方向如图2-2中所示。
在单轴柔性铰链设计中，最关键的是绕Z轴方向的转角刚度的设计计算，下面将对几种常见类型的铰链作分析研究。
柔性铰链的拉伸刚度和转角刚度的计算公式[1]： 1) 拉伸刚度的推导当在X 轴向施加拉力F x 时，铰链伸长量为：1()2()x x x xF F x dx dx EA x Eb f x ∆==⎰⎰，则拉伸刚度为：12/()xEb dx f x ⎰。
2) 转角刚度的推导当在Z 轴回转方向施加弯矩Mx 时，铰链转角为331()2()x xxxM M dx dx EI x Eb f x θ==⎰⎰，则转角刚度为：321/3()xEb dx f x ⎰。
式中，()f x 为柔性铰链形状的表达函数，E 为材料的弹性模量。
a 、单轴直梁型柔性铰链单轴直梁型柔性铰链如图2-2所示，其应用广泛。
单轴直梁型柔性铰链沿X 轴方向的拉伸刚度和绕Z 轴的转角刚度可以利用上面给出的公式进行计算。
图2-2 单轴直梁型柔性铰链Fig. 2-2 Flexure hinge with rectangle notch根据上面的公式可得，单轴直梁型柔性铰链的拉伸刚度为Ebt ，转角刚度为312Ebt 。
也就是说单轴直梁型柔性铰链的拉伸刚度与t 、b 成正比，转角刚度与3t 、b 成正比；由此可知，在拉伸刚度限定的情况下，为了提高其弯曲率，应尽量加大b 值而减小t 值。
b 、单轴直圆型柔性铰链单轴直圆型柔性铰链如图2-3所示，对于单轴直圆型柔性铰链的设计计算，在1965年， J.M.Paros 等就推导出tR 条件下的设计计算公式（包括精度计算公式和简化计算公式），但其精确计算公式形式比较复杂，简化后的设计计算公式在许多情况下误差又比较大。
在1988年，清华大学的高宏等从微位移机构的实际情况出发，对用于微位移机构的柔性铰链图2-3 单轴直梁型柔性铰链Fig. 2-3 Flexure hinge with circle notch进行了分析，发现其机构具有两个明显的特点：一是位移量（即柔性铰链的变形比较小），一般是几十微米到几百微米；二是结构参数在一般情况下取t R，并根据这两个特点推导了简化设计方法，最后给出了几种不同参数下柔性铰链的转角刚度数表。
为了能对单轴直圆型柔性铰链的设计计算给出准确可靠的设计计算公式，Y.K. Yong和T.F. Lu等利用有限元分析方法给出了单轴直圆型柔性铰链的经验设计公式，并利用此分析结果对已有的设计理论和方法做了对比，其结果如表2-5所示。
研究团队z zMα(t/R的范围)误差百分比y yF∆(考虑剪切模量)(t/R)误差百分比x xF∆(t/R的范围)误差百分比最小最大平均最小最大平均最小最大平均Paros and Weisbord(完全公式) 0.05≤t/R＜0.11.8 5.0 3.50.05≤t/R≤0.12 4 3.10.25≤t/R≤0.650.3 4.9 2.4Paros and Weisbord(简化公式) 0.05≤t/R≤0.21.2 4.9 3.10.05≤t/R≤0.13 5.6 4.3 无Lobontiu 0.05≤t/R＜0.11.8 5.0 3.50.05≤t/R≤0.12 3.9 2.90.25≤t/R≤0.650.3 4.9 2.4Wu and Zhou 0.05≤t/R＜0.11.8 5.0 3.50.05≤t/R≤0.12 4 3.10.25≤t/R≤0.650.3 4.9 2.4Tseytlin 0.4≤t/R≤0.60.7 4.5 2.5 无无Smith 0.2≤t/R≤0.650.8 3.7 2.4 无无Schotborgh 0.05≤t/R≤0.650.032.5 1.2 无无Yong 无0.05≤t/R≤0.80 2.7 0.070.05≤t/R≤0.80 1.1 0.08随着柔性铰链理论的不断完善，与之相关的柔性微动工作台也逐渐产业化。
为了能更好地指导工程实践，本文将对便于工程应用的简化设计方法做一些完善。
单轴直圆型柔性铰链转角刚度计算的计算简图，如图2-4所示，柔性铰链的转角变形实际上是由许多微段弯曲变形累积的结果，设第i 个微段产生i θ∆的转角和i y ∆的挠度，则整个柔性铰链的转角θ和挠度y 为1nii θθ==∆∑和1nii y y ==∆∑。
图2-4 单轴直梁型柔性铰链 Fig. 2-4 Flexure hinge with circle notch设连续变化的截面由若干长度为dx 的等截面微段所组成，由材料力学的知识可得柔性铰链中性面的曲率半径ρ：1()()M x EJ x ρ=(2-2)式中，E 为材料的弹性模量；()J x 为截面对中心轴的惯性矩；()M x 为作用在微段dx 上的弯矩。
