下载文档原格式
饮酒驾车问题的数学模型按照国家质量监督检验检疫总局《车辆驾驶人员血液、呼气酒精含量阈值与检验》规定,饮酒驾车指:车辆驾驶人员血液中的酒精含量大于或者等于20mg/100mL,小于80mg/100mL的驾驶行为。
醉酒驾车指:车辆驾驶人员血液中的酒精含量大于或等80mg/100mL的驾驶行为。
那么酒后什么时候酒精浓度最高,酒后到底多长时间才能安全驾车下面我们就此问题建立数学模型。
一、提出问题体重为70kg的人在喝下(认为是瞬时饮酒)1瓶啤酒后,测量他的血液中酒精含量(毫克/百毫升),得数据[1]如下问题1.饮酒后多长时间后血液中含酒精量最大。
问题2.某人在早上8点喝了一瓶啤酒,下午2点检查时符合新的驾车标准,他在19点吃晚饭时又喝了一瓶啤酒,过了6小时后驾车回家,又一次遭遇检查时却被定为饮酒驾车,这让他陷入困惑,为什么喝同样多的酒,两次检查结果会不一样呢过六小时后再喝一瓶,过多长时间才可以驾车。
问题3.一次喝3瓶啤酒多长时间可以驾车。
二、基本假设短时间饮酒是一次饮入,中间时差不计。
酒精在血液与体液中含量相同。
酒精进入体内后不受其他因素对酒精的分解,不考虑个体差异。
转移过程为,胃→体液→体外。
人的体液占人体重的65%至70%,血液占体重的7%左右;而酒精在血液与体液中的含量是一样的。
三、参数说明t为饮酒时间,y1(t)为时刻人体消化的酒精量,y2(t)为时刻人体的酒精量,k1为酒精在人体中的吸收率常数,k2为酒精在人体中的消除率常数,c(t)为时刻内血液中酒精浓度。
f为酒在人体的吸收度(为一常数,其值等于血液与体液的重量之比)。
四、模型建立与求解可把酒精在体内的代谢看成进与出的过程,用和分别表示酒精输入速率和酒精输出速率,这样问题可简化为血液中酒精的变化律等于输入速率减去输出速率,即。
通过一系列计算得到人体内酒精含量。
可以看出,当酒精含量最大,解得,且此时c(t)达到最大值。
五、问题的回答 1.饮酒后多长时间后血液中含酒精量最大。
![数学建模例题_之_饮酒驾驶模型[1]](https://img.taocdn.com/s1/m/1b60a21ec281e53a5802ff30.png)
饮酒驾驶模型摘要本文针对酒后驾车造成交通事故死亡率高，以及根据国家质量检验检疫局发布的饮酒后驾车新标准，建立了饮酒后血液中酒精含量的数学模型。
通过了解酒精在体内吸收，分布和排除的动态过程，及这些过程与人体内酒精反应的定量关系建立微分方程，运用药物动力学原理建立单室和双室模型。
得出血液中的酒精含量)(t C ,与进入体内总酒量)(t x 、时间t 的函数关系式：单室模型：()()()()k k e e x k t x t C a t k kt a a --==--0双室模型：()()n n p n p t pt pt v t x v t x AUC AUC n n∆⎪⎪⎭⎫⎝⎛++=--1001本文还运用了 Wagner-Nelson 法（待吸收的百分数对时间作图法），与题中给出的参考数据在计算机运行的结果作对比。
本文还解决了如下问题：1、从模型分析了大李第二次被判为饮酒驾车是因为二次饮酒，而使血液中酒精含量累积而超标。
2、对喝了低度酒多长时间驾车违反规则作了量化分析；3、从单室模型得出了一个血液中酒精含量峰值计算公式：()k k k gk t a a -=303.2max4、用本文的模型对天天喝酒能否开车作了讨论。
本文最后对模型的优点和不足作了评价。
一、问题提出据报载，2003年全国道路交通事故死亡人数为10.4372万，其中因饮酒驾车造成的占有相当的比例。
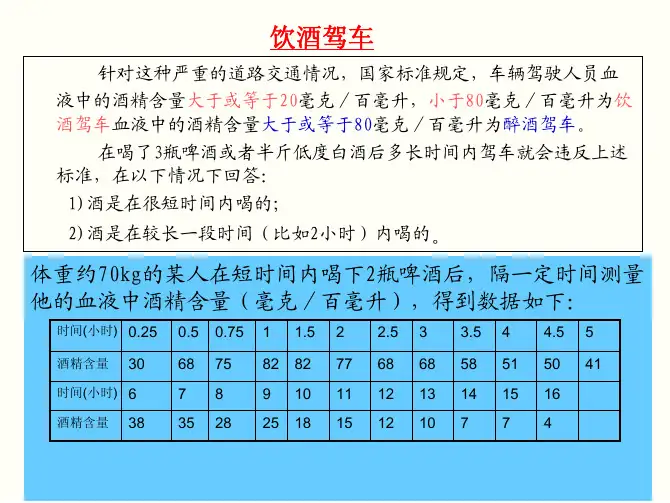
大李在中午12点喝了一瓶啤酒，下午6点检查时符合新的驾车标准，紧接着他在吃晚饭时又喝了一瓶啤酒，为了保险起见他呆到凌晨2点才驾车回家，又一次遭遇检查时却被定为饮酒驾车，这让他既懊恼又困惑，为什么喝同样多的酒，两次检查结果会不一样呢？请你参考下面给出的数据（或自己收集资料）建立饮酒后血液中酒精含量的数学模型，并讨论以下问题：1. 对大李碰到的情况做出解释；2. 在喝了3瓶啤酒或者半斤低度白酒后多长时间内驾车就会违反上述标准，在以下情况下回答：1）酒是在很短时间内喝的；2）酒是在较长一段时间（比如2小时）内喝的。
分段函数模型在实际问题中的应用数学应用意识的考查是高考命题的指导思想，考查应用意识是通过解答应用问题来体现的，考查的重点是客观事物的数学化，这个过程主要是依据现实生活的背景，提炼相关的数量关系，构造数学模型，将现实问题转化为数学问题，并加以解决。
本文就分段函数模型在几种实际问题中的应用举例加以说明，供同学们学习时参考。
一． 醉酒驾车问题举例1. 某驾驶员喝了m 升酒后，血液中的酒精含量f(x)(毫克/毫升)随时间x(小时)变化的规律近似地满足表达式f(x)=()⎪⎩⎪⎨⎧>⋅≤≤-1,10,531532x x x x 。
《酒后驾车与醉酒驾车的标准及相应的处罚》规定: 驾驶员血液中的酒精含量不得超过0.02毫克/毫升.此驾驶员至少要过______小时后才能开车。
(精确到1小时)分析:本题为分段函数型。
根据解答分段函数“对号入座”的解题原则，分别利用两段函数表达式求解。
解析:当0≤x ≤1时,f(x)为增函数，f(x )≥50-2=0.04>0.02；当x>1时, f(x)=()x 3153⋅≤0.02得()x 31≤301，3x ≥30, 33=27<30, 34=81>30,x ≥4,故该驾驶员至少要过4小时后才能开车.二 工作安排问题举例2 某车间有50名工人，要完成150件产品的生产任务，每件产品由3个A 型零件和1个B 型零件配套组成，每个工人每小时能加工5个A 型零件或者3个B 型零件，现在把这些工人分成两组同时工作(分组后人数不再进行调整)，每组加工同一种型号的零件。
设加工A 型零件的工人人数为x 名(*∈N x ).⑴分别用含x 的式子表示完成A 型零件加工所需时间和完成B 型零件加工所需时间； ⑵为了在最短时间内完成全部生产任务，x 应取何值?解析: ⑴生产150件产品，需加工A 型零件450个，则完成A 型零件加工所需时间f(x)= ()491,905450≤≤∈=*x N x x x . 生产150件产品，需加工B 型零件150个，则完成B 型零件加工所需时间g(x)=()()491,5050503150≤≤∈=*--x N x x x . (2)设完成全部生产任务所需时间为h(x)小时，则h(x)为f(x)与g(x)的较大者。
合理判断酒驾模型从2011年5月1日新交规开始实施，警察查酒驾依据的标准是：血液中酒精含量<20mg/100ml，合格；血液中酒精含量 20mg/100ml， <80mg/100ml，为酒后驾驶；血液中酒精含量>80mg/100ml，为醉酒驾驶。
具体喝多少酒就达到酒后或醉酒标准呢？警察是用酒精测试仪进行现场测定的，对着测试仪呼一口气，酒精含量马上就会显示出来。
如果达到醉酒或酒后标准，当事人可提出异议，警察可以安排抽血化验血液中酒精含量，一般要第二天出结果。
如果当事人从酒精测试仪没有提出异议，测试结果可作为处罚依据。
有人计算出了各种酒的临界值：表1喝酒后血液中酒精含量与人的体重、酒的度数高低、饮酒后休息的时间有关，与个体的酒量没有任何关系。
一般来说，体重大的人血液量也会增加，酒精度数越高（白酒>黄酒>红酒>啤酒），就越容易达到酒后驾驶标准。
北京大学综合医院营养科主任朱翠凤博士说，根据个人体质、性别、年龄等具体情况不同，计算血液里酒精含量的方法也不同。
酒喝到体内，胃和肝脏都能分泌分解酒中酒精的酶，其中95％的酒精是在肝脏被分解的。
同样的酒量，如体内分泌分解酒精的酶多，则酒精被分解得多，那么进入血中的酒精就少，决定酒量大小的最主要因素是体内分泌分解酒精酶的能力大小。
“一个人的酒量大小很大程度是天生的。
”海慈医院营养科副主任杨红：一个人的酒量大小，很大程度上由遗传因素决定，能喝的人天生就能喝，但如果不能喝酒却硬多喝，对身体有很大的影响。
酒在人体内的分解与时间明显相关参考数据1. 人的体液占人的体重的65%至70%，其中血液只占体重的7%左右；而药物（包括酒精）在血液中的含量与在体液中的含量大体是一样的.2. 体重约70kg的某人在短时间内喝下2瓶啤酒后，隔一定时间测量他的血液中酒精含量（毫克／百毫升），得到数据如下：时间(小时) 酒精含量0.25 300.5 680.75 751 821.5 822 772.5 683 683.5 584 514.5 505 416 387 358 289 2510 1811 1512 1213 1014 715 716 4请查阅或收集相关资料，建模回答下列问题：（1）表1中给出的饮用各种酒的“酒后驾驶标准”和“醉酒驾驶标准”合理否？制订你认为合理的评判标准。
实验6.8“饮酒驾车的药物注射模型”求解一·实验目的运用药物注射模型，使用曲线拟合方法，解释饮酒驾车的一些实际问题二·实验原理由于酒精不需要进入肠道即可被吸收，且胃对其吸收速率也非常快，本题应采用“快速静脉注射模型”。
酒精主要存在于血液中，故本例应计算吸收室的血药浓度c1(t)=A1*e^(-αt)+B1*e(-βt)相关系数可以通过拟合法求解。
三·实验代码>> t=[0.25,0.5,0.75,1,1.5,2,2.5,3,3.5,4,4.5,5,6,7,8,9,10,11,12,13,14,15,16];>> y=[30,68,75,82,84,77,70,68,58,51,50,41,38,35,28,25,18,15,12,10,7,7,4];>> ft=fittype('A1*exp(-a*x)+B1*exp(-b*x)');>> options=fitoptions('Method','NonlinearLeastSquares');>> options.StartPoint=[0 -1000 0 0];>> cfit=fit(t',y',ft,options);>> plot(cfit,t',y','o');//拟合曲线1>> A1=cfit.A1>> B1=cfit.B1>> a=cfit.a>> b=cfit.b>> t1=6;>> c1=(A1*exp(-a*t1)+B1*exp(-b*t1))/2>> t2=13.2;>> c2=(A1*exp(-a*t2)+B1*exp(-b*t2))/2>> t3=7.2;>> c3=(A1*exp(-a*t3)+B1*exp(-b*t3))/2>> t2=0.2:0.1:24;>> for i=1:239c2(i)=(A1*exp(-a*t2(i))+B1*exp(-b*t2(i)))/2;end>> plot(t2,c2,t2,20);>> plot(cfit,t',y','o');//拟合曲线2>> t4=0.2:0.1:72>> for i=1:length(t4)c4(i)=(A1*exp(-a*t4(i))+B1*exp(-b*t4(i)))*1.5;end>> for i=121:length(t4)c42(i)=(A1*exp(-a*t4(i-120))+B1*exp(-b*t4(i-120)))*1.5;end>> for i=241:length(t4)c43(i)=(A1*exp(-a*t4(i-240))+B1*exp(-b*t4(i-240)))*1.5;end>> for i=361:length(t4)c44(i)=(A1*exp(-a*t4(i-360))+B1*exp(-b*t4(i-360)))*1.5;end>> for i=481:length(t4)c45(i)=(A1*exp(-a*t4(i-480))+B1*exp(-b*t4(i-480)))*1.5;end>> for i=1:length(t4)c4A1(i)=c4(i)+c42(i)+c43(i)+c44(i)+c45(i);c4A2(i)=c4(i)+c43(i)+c45(i);end>> plot(t4,c4A1,t4,20);//拟合曲线3>> plot(t4,c4A2,t4,20);//拟合曲线4四·代码结果1.问题：根据表格数据拟合求解相关系数A1=110.55B1=-151.46a=0.17949b=2.8243拟合曲线如下2.问题：某人中午12点喝了一瓶啤酒，下午6点检查合格，晚饭又喝了一瓶，次日凌晨2点检查未通过，请解释此情况。
数学建模饮酒驾车题及建模论文饮酒驾车据报载，2003年全国道路交通事故死亡人数为10.4372万，其中因饮酒驾车造成的占有相当的比例。
针对这种严重的道路交通情况，国家质量监督检验检疫局2004年5月31号发布了新的《车辆驾驶人员血液、呼气酒精含量阈值与检验》国家标准，新标准规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克／百毫升，小于80毫克／百毫升为饮酒驾车（原标准是小于100毫克／百毫升），血液中的酒精含量大于或等于80毫克／百毫升为醉酒驾车（原标准是大于或等于100毫克／百毫升）。
大李在中午12点喝了一瓶啤酒，下午6点检查时符合新的驾车标准，紧接着他在吃晚饭时又喝了一瓶啤酒，为了保险起见他呆到凌晨2点才驾车回家，又一次遭遇检查时却被定为饮酒驾车，这让他既懊恼又困惑，为什么喝同样多的酒，两次检查结果会不一样呢？请你参考下面给出的数据（或自己收集资料）建立饮酒后血液中酒精含量的数学模型，并讨论以下问题：1.对大李碰到的情况做出解释；2.在喝了3瓶啤酒或者半斤低度白酒后多长时间内驾车就会违反上述标准，在以下情况下回答：1）酒是在很短时间内喝的；2）酒是在较长一段时间（比如2小时）内喝的。
3.怎样估计血液中的酒精含量在什么时间最高。
4.根据你的模型论证：如果天天喝酒，是否还能开车？5.根据你做的模型并结合新的国家标准写一篇短文，给想喝一点酒的司机如何驾车提出忠告。
参考数据1.人的体液占人的体重的65%至70%，其中血液只占体重的7%左右；而药物（包括酒精）在血液中的含量与在体液中的含量大体是一样的。
2.体重约70kg的某人在短时间内喝下2瓶啤酒后，隔一定时间测量他的血液中酒精含量（毫克／百毫升），得到数据如下：酒后不开车摘要近年来，因饮酒、醉酒驾车而造成的交通事故频发，且呈逐年上升趋势。
加强司机的安全观念成为重中之重。
和大李一样困惑的司机也不在少数，问题1我们便会对大李所遇到的情况加以科学地解释；问题2我们要将情况推广，在喝酒持续时间长短两种情况下讨论酒后驾车的合理时间间隔；在问题2的基础上，进而我们引出问题3来研究酒后人体血液中的酒精含量出现最高的时间点；问题4是帮助那些想每天喝酒的司机来协调他们喝酒和开车的问题。
目录摘要 (1)一. 问题重述………………………………………………………二.问题分析…………………………………………………………三. 模型假设…………………………………………………………四.符号说明…………………………………………………………五.模型的建立与求解………………………………………………快速饮酒的模型……………………………………………慢速饮酒的模型……………………………………………多次饮酒模型………………………………………………六.模型的评价与改造…………………………………………………解释题目中大李遇到的问题…………………………………喝了三瓶酒或半斤底度白酒后多久才能驾车………………估计血液中酒精含量在何时最高……………………………天天喝酒,能否开车……………………………………………给司机的忠告……………………………………………………七.模型评价…………………………………………………………………八.模型推广…………………………………………………………………九.参考文献…………………………………………………………………十.附录………………………………………………………………………一、问题重述关键词：微分方程、模型。
本问题主要是分析驾驶员在喝过一定量的酒后，血液中酒精含量上升，影响司机驾车，所以司机饮酒后需经过一段时间后才能安全驾车，国家标准新规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升，小于80毫克/百毫升为饮酒驾车，血液中酒精含量大于或等于80毫克/百毫升为醉酒驾车，司机大李在中午12点喝下一瓶啤酒，6小时后检查符合新标准，晚饭地其又喝了一瓶啤酒，他到凌晨2点驾车，被检查时定为饮酒驾车，为什么喝相同量的酒，两次结果不一样讨论问题：1. 对大李碰到的情况做出解释；2. 在喝了3瓶啤酒或者半斤低度白酒后多长时间内驾车就会违反上述标准，在以下情况下回答：1）酒是在很短时间内喝的；2）酒是在较长一段时间（比如2小时）内喝的。
3. 怎样估计血液中的酒精含量在什么时间最高。
4. 根据你的模型论证：如果天天喝酒，是否还能开车5. 根据你做的模型并结合新的国家标准写一篇短文，给想喝一点酒的司机如何驾车提出忠告。
参考数据1. 人的体液占人的体重的65%至70%，其中血液只占体重的7%左右；而药物（包括酒精）在血液中的含量与在体液中的含量大体是一样的。
2. 体重约70kg的某人在短时间内喝下2瓶啤酒后，隔一定时间测量他的血液中酒精含量（毫克／百毫升），得到数据如下：二、模型假设1、酒精从胃转移到体液的速率与胃中的酒精浓度成正比。
2、酒精从体液转移到体外的速率与体液中的酒精浓度成正比。
3、酒精从胃转移到体液的过程中没有损失，且不考虑误差。
三、符号说明k 0:酒精从体外进入胃的速率；f 1(t):酒精从胃转移到体液的速率；f 2(t):酒精从体液转移到体外的速率；X(t):胃里的酒精含量；Y(t)：体液中酒精含量；V 0:体液的容积；K 1:酒精从胃转移到体液的速率系数；K 2:酒精从体液转移到体外的速率系数；C(t):体液中的酒精浓度。
0D ：短时间喝酒情况下进入胃中的初始酒精量。
T ：较长时间喝酒所用的时间或达到浓度最大值所需时间。
四、模型的分析与建立（一）、模型分析：假设酒精先以速率0k 进入胃中，然后以速率)(1t f 从胃进入体液，再以速率f 2(t)从体液中排到体外。
（二）模型建立：找到C(t)与t 的关系用x(t)与y(t)分别表示酒精在胃、体液中的酒精量，c(t)表示酒精在体液中的浓度。
根据前面的假设可知：)()(11t x k t f =)()(22t y k t f =1.对胃建立方程： dx(t)=k 0dt-f 1(t)dt)()(10t f k dt t dx -= 可得：01)()(k t x k dtt dx =+ 利用一阶线性常微分方程求解，可以得到；⎪⎪⎩⎪⎪⎨⎧==+=+=-01110111)0()(1x x A c k k A A e c t x t k 又因为)()(11t x k t f = ，联合式可得：111111)(A k e c k t f t K +=-0111k e c k t k +=-00011)(k ek x k t k +-=-2又对中心室可建立方程组如下； ⎪⎩⎪⎨⎧=-=021)0()()()(y y t f t f dt t dy 同理：)()()(21t y k t f dtt dy -= 因为000111)()(k e k x k t f t k +-=-，将其代入上式可得到：000121)()()(k e k x k t y k dtt dy t k +-=+- 利用微分求解：t k t k t k t k e B A e c e k k k x k k k e c t y 121222212001202)(----++=--++= 又酒精浓度为酒精量与体液容积之比，0)()(v t y t c =，即： t k t k e B A e c t c 12333)(--++=（其中 023v c c =，0203v k k A =，0120013)(v k k k x k B --=，0333)0(c c C B A ==++）。
（三）模型的讨论：情况一 1当酒是在较短时间内喝时此时有00)0(x D x ==，00=k ，00=c 。
由上可得：03=A ，012013)(v k k D k B -=，33B c -= 因此有：]333121212[)()(t k t k t k t k tk t k e e A e e B e B e B t c -------=--=+-= （其中 021013)(v k k D k B A -=-=） 设K1>K2,因此可认为：t k Ae t c 2)(-≈t K A t c 2ln )(ln -=⇒利用数表一：（喝下两瓶啤酒 取小时以后）通过Matlab 进行曲线拟合可得：>> t=[ 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16];y1=[82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7 4];y2=log(y1);polyfit(t,y2,1);ans =5459.118=A ，1940.02=k根据查阅资料可知：一瓶啤酒的酒精量一般为640ml ，密度为810mg/ml 酒精浓度不超过%，所以两瓶啤酒的酒精总量mg D 46656%5.481064020=⨯⨯⨯=由于体重为70kg,体重的65%左右，体液密度为ml 33.43310005.110%657030=⨯⨯⨯=v 毫克/百毫升。
由02101)(v k k D k A -=可求得：114.21=k 。
可得短时间内喝下两瓶啤酒时关系式如下；][5459.118)(114.21940.0t t e e t c ---=用Matlab 软件画出图形为：情况二1当酒是在较长时间内喝时我们可将其进行分段讨论。
当t ](，T0∈时，同样可以得到：T 为喝酒总用时，取2小时。
此时TD k 00=，x （0）=0，y （0）=0因为： t k t k e B A e c t c 12333)(--++=可知)()1()()(12223313333t k t k t k tk t k e e B e A e B A e B A t c --------=+++-=由上式可以求得：A 3=B 3=所以可得 :T k T k T k T k T k t k Be e e B e e B e A T c 212122][)()1()(33------=-=---=2当t T >时，则此时血液中的浓度与时间关系式如下： )(2)(1)(20211)(][)()()(T t k T t k T t k e T C e e v k k T x k t c ------+-⨯-= 其中]1[1)(110011001T k T k e k k k k e k k x k T x ---=+-= ][)(]1[)(212102020T k T k T k e e k k k e y k k T c -----+-= 综上所述，可得，当T t ≥时⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--+-=-=+-⨯-=----------][]1[)(]1[)()(][)()()(212121*********)()()(0211T k T k t k T k T t k T t k T t k e e k k k e y k k T c e k k T x e T C e e v k k T x k t c五、问题的解答问一：假设大李第一次喝酒是在短时间内喝的，根据所建立模型，符合情况一][27295.59)(114.21940.0t t e e t c ---=（一瓶啤酒）当6=t 时，可以求得百毫升/2778.18)(mg t c =，小于200mg/百毫升，所以第一次检查时不是饮酒驾驶。
紧接着他在吃晚饭时又喝了一瓶啤酒，为了保险起见他呆到凌晨2点才驾车回家，又一次遭遇检查时却被定为饮酒驾车。
第一次喝完6小时后残余百毫升，又过8小时残余百毫升，因此晚六点喝酒不是短时间喝完，因此可知，+=＞20。
因此为饮酒驾车。
问二（1）当酒是在较短时间内喝时，符合情况一所以：三瓶啤酒时 ][81885.177)(114.21940.0t t e e t c ---=当百毫升毫克/20)(=t c 时，可求得小时261.11=t 。
所以当驾驶员在较短时间内喝下三瓶啤酒时，必须经过小时后开车才不会被认为是饮酒驾车。
（2）当酒是在较长时间内喝时，符合情况二t k t k e B A e c t c 12333)(--++=当百毫升毫克/20)(=t c 时，可以求出407.13=t 小时，所以当驾驶员在较长时间（T 为二小时）喝下三瓶啤酒后，必须经过小时后开车才不被认为是饮酒驾车。
问三：（1） 短时间内喝酒时，符合情况一 ][)()(1202101t k t k e e V K K D k t c ----=当)(t c 的导数等于0时，可解得：23.1212ln 1ln =--=k k k k T 所以当t=时，)(t c 取得最大值。
（2）、当酒是在较长时间内喝时，符合情况二在第二小时时含量最高。
问四:假设天天喝酒,每次喝酒为短时间喝完。
C （t ）=2122k t k t n n Ae Ae ---＜20，可知n ＜2 即每天喝小于两瓶符合。
