饮酒驾车的数学模型摘要本文解决的是一个司机安全驾车与饮酒的问题，目的是通过建立一个数学模型（结合新的国家驾驶员饮酒标准）分析司机如何适量饮酒不会影响正常的安全驾驶。
根据一定合理的假设，建立人体内酒精浓度随时间变化的微分方程模型，并通过拟合曲线对数据进行分析。
在不同饮酒方式下进行分类讨论，得出体内酒精浓度随时间的变化函数。
在讨论过程中，我们得到两个结论：在短时间喝酒形式下，达到最大值的时间为1.23小时，与喝酒量无关；在长时间喝酒形式下，喝酒结束时酒精含量最高。
最后，我们讨论了模型的优缺点，并结合新的国家标准写一篇关于司机如果何适量饮酒的一篇短文。
关键词：微分方程、模型、房室系统。
一、问题重述据报载，2008年全国道路交通事故死亡人数为10.4372万，其中饮酒驾车造成的占有相当的比例。
针对这种严重的道路交通情况，国家质量监督检验检疫局2004年5月31日发布了新的《车辆驾驶人员血液呼气酒精含量值与检验》国家标准，新标准规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升，小于80毫克/百毫升为饮酒驾车，血液中酒精含量大于或等于80毫克/百毫升为醉酒驾车。
司机大李在中午12点喝下一瓶啤酒，6小时后检查符合新标准，晚饭地其又喝了一瓶啤酒，他到凌晨2点驾车，被检查时定为饮酒驾车，为什么喝相同量的酒，两次结果不一样？请你参考下面给出的数据（或自己收集资料）建立饮酒后血液中酒精含量的数学模型，并讨论以下问题：1、对大李碰到的情况做出合理解释；2、在喝三瓶啤酒或半斤白酒后多长时间内驾车会违反标准，在以下情况回答：1)酒食在很短时间内喝的：2）酒食在较长一段时间(比如两小时)内喝的3、怎样估计血液中的酒精含量在什么时间最高；4、根据你的模型论证：如果该司机想天天喝酒，是否还能开车？5、根据你做的模型结合新的国家标准写一篇短文，给想喝一点酒的司机如何驾车提出忠告。
二、模型假设1、酒精从胃转移到体液的速率与胃中的酒精浓度成正比。
2、酒精从体液转移到体外的速率与体液中的酒精浓度成正比。
3、酒精从胃转移到体液的过程中没有损失。
4、测量设备完善，不考虑不同因素所造成的误差。
5、酒精在体液中均匀分布。
三、符号说明k:酒精从体外进入胃的速率；(t):酒精从胃转移到体液的速率；f1(t):酒精从体液转移到体外的速率；f2X(t):胃里的酒精含量；Y(t)：体液中酒精含量；:体液的容积；V:酒精从胃转移到体液的转移速率系数；K1K:酒精从体液转移到体外的转移速率系数；2C(t):体液中的酒精浓度。
D：短时间喝酒情况下进入胃中的初始酒精量。
T：较长时间喝酒所用的时间或达到浓度最大值所需时间。
四、模型的分析与建立（一）、模型分析：假设酒精先以速率0k 进入胃中，然后以速率)(1t f 从胃进入体液，再以速率f 2(t)从体液中排到体外。
根据假设可以建立如图一所示的带有吸收室的单房室系统，其中胃为吸收室，体液为中心室。
图一（二）模型建立：用x(t)与y(t)分别表示酒精在胃、体液中的酒精量，c(t)表示酒精在体液中的浓度。
根据酒精从胃进入体液的速度f 1(t)与胃中的酒精量成正比，速率系数为K 1；酒精从血液中排出的速率f 2(t)与血液中的酒精量y(t)成正比，速率系数为K 2，可以建立方程如下：)()(11t x k t f =（1） )()(22t y k t f = （2）)()(10t f k dtt dx -= （3）将（1）式代入（3）式可得：)()(10t x k k dtt dx -= （4）通过移项，上式可以转化为； 01)()(k t x k dtt dx =+ （5） 利用一阶线性常微分方程的常数变易法对（5）式求解，可以得到； ⎪⎪⎩⎪⎪⎨⎧==+=+=-01110111)0()(1x x A c k k A A e c t x t k （6）又因为)()(11t x k t f = ，联合（6）式可得：111111)(A k e c k t f t K +=- （7） 0111k e c k t k+=-00011)(k e k x k t k+-=-又对中心室（即体液）可建立方程组如下；⎪⎩⎪⎨⎧=-=021)0()()()(y y t f t f dt t dy（8） 将（2）式代入（8）式可得；)()()(21t y k t f dt t dy -=将上式转化为： )()()(12t f t y k dt t dy =+因为000111)()(k e k x k t f tk +-=-，将其代入上式可得到： 000121)()()(ke k x k t y k dt t dy t k +-=+- （9） 求解可得；tkt ktkt k e B A e c ek k k x k k k e c t y 121222212001202)(----++=--++=（10） （其中 202k k A =， 120012k k k x k B --=，0222)0(y y c B A ==++） 又酒精浓度为酒精量与体液容积之比，0)()(v t y t c =，即：tk t k e B A e c t c 12333)(--++=（11） （其中 023v c c =，0203v k k A =，0120013)(v k k k x k B --=，0333)0(c c C B A ==++）。
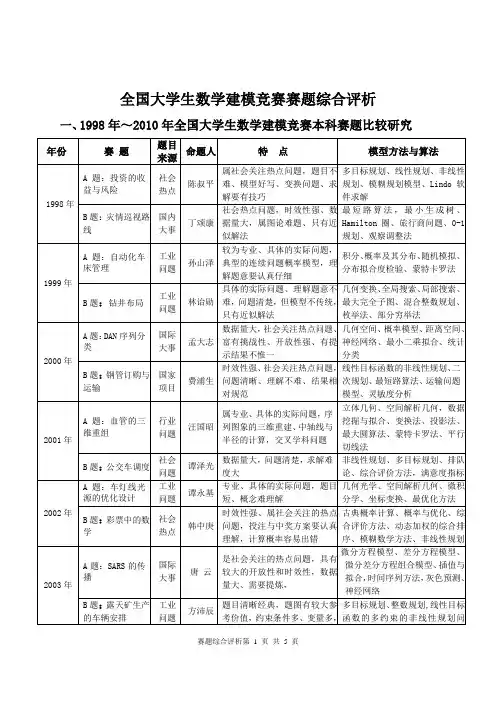
（三） 模型的讨论：1、当酒是在较短时间内喝时此时有： 00)0(x D x ==，00=k ，00=c 。
因为有： 0203v k k A =，0120013)(v k k k x k B --=，023v c c = 所以经计算整理后可得：03=A ，012013)(v k k D k B -=，33B c -= 将A 3，B 3，C 3代入式（11）可以得到：酒在较短时间内喝下去时，体液中的酒精浓度与时间的函数关系式如下所示：]333121212[)()(t k t k t k t k tk t k e e A e e B e B e B t c -------=--=+-= （12）（其中 021013)(v k k D k B A -=-=） 当t 比较大时，显然K1>>K2,因此可认为：t k Ae t c 2)(-≈t K A t c 2ln )(ln -=⇒利用数表一：通过Matlab 进行曲线拟合可得：5459.118=A ，1940.02=k根据查阅资料可知：一瓶啤酒的酒精量一般为640ml ，密度为810mg/ml 酒精浓度为84.5%所以两瓶啤酒的酒精总量mg D 46656%5.481064020=⨯⨯⨯=由于体重为70kg,体重的65%左右，体液密度为1.05mg/ml ，所以可得体液的总体积为33.43310005.110%657030=⨯⨯⨯=v 毫克/百毫升。
由： 02101)(v k k D k A -= 可求得： 114.21=k 。
可得短时间内喝下两瓶啤酒时血液中的酒精含量与时间的关系式如下；][5459.118)(114.21940.0t t e e t c ---= （13）用Matlab 软件画出图形为：（图二：拟合曲线）1、当酒是在较长时间内喝时我们可将其进行分段讨论。
当t ](，T 0∈时，同样可以得到： ⎪⎪⎩⎪⎪⎨⎧-=-=)()()()()(2210t y k t f dtt dy t x k k dt t dx （14）但此时： TD k 00=，x （0）=0，y （0）=0 可得： t k t k e B A e c t y 12222)(--++=（其中A 2=20k k ，120012k k k x k B --=，0222)0(y y C B A ==++）根据上式可得到：t k t k e B A e c t c 12333)(--++=（ 其中 023x c c =， A 3=020y k k ， 0120013)(v k k k x k B --=） 即： )()1()()(12223313333t k t k t k tk t k e e B eA eB A e B A t c --------=+++-= （15） 可以求得：A 3=5025909.27732.4331940.0246656020020=⨯⨯==v Tk D v k k B 33.433)114.21940.0(246656)()(012001203⨯--=--=--=v k k T D v k k k =28.0386772 所以可得 :T k T k T k T k T k t k Be e e B e e B e A T c 212122][)()1()(33------=-=---= （16）当t T >时，则此时血液中的浓度与时间关系式如下： )(2)(1)(20211)(][)()()(T t k T t k T t k e T C e e v k k T x k t c ------+-⨯-= 其中： ]1[1)(110011001T k T k e k k k k e k k x k T x ---=+-= ][)(]1[)(212102020T k T k T k e e k k k e y k k T c -----+-=综上所述，可得，当T t ≥时⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--+-=-=+-⨯-=----------][]1[)(]1[)()(][)()()(212121*********)()()(0211T k T k t k T k T t k T t k T t k e e k k k e y k k T c e k k T x e T C e e v k k T x k t c （17） 五、问题的解答问题一：假设大李第一次喝酒是在短时间内喝的，根据所建立模型，可知人体中血液中的酒精含量与时间的函数关系式如下；][0)21(01)(12t k t k e e v k k D k t c ----= 根据求解可得，114.21=k ，1940.02=k ，mg D 233280=，33.4330=v 。
所以可求得， ][27295.59)(114.21940.0t t e e t c ---=当6=t 时，可以求得百毫升/2778.18)(mg t c =，小于国家规定的新标准，所以第一次遭遇检查时没有被认定为是饮酒驾驶，见图二图三接着，大李在吃晚饭时又喝了一瓶啤酒，此时大李体内还留有第一次喝后残留酒精，所以第二次体内的酒精含量，应该是二喝酒后体内酒精的叠加，此时我们认为大李是在较长时间内喝的，根据所建模型，有：][][)()()(1212T t k T t k t k t k e e A e e A t c -------+-= 已知，A=59.27295,k 2=0.1940,k 1=2.114,T=6.所以可以求出当t=14时，ml mg t c 100/3618.20)(=大于国家新规定的20mg/100ml,所以第二次虽然迟了二个小时，但检查出来时，酒精还是超标的，见下图：图四所以从以上分析可知，虽然大李是喝相同量的酒，且第二次检查时离喝酒时间比第一次延长了二个小时，但由于第一次喝后体内还留有第一次剩余的酒精，并且第二次是较长时间内喝的比第一次短时间内喝的达到标准所需时间要大，所以第二次会被认定是饮酒驾车，大李的这种遭遇我们可知，一个人人体内血液中的酒精含量不仅与所喝的酒量有关，而且还与喝酒所用的时间快慢及体内血液中原来的酒精含量也有关。
