福建省厦门双十中学2014届高三热身考试试卷(1)
- 格式:doc
- 大小:1.02 MB
- 文档页数:12

福建省厦门双十中学高三热身考试题语文(本试卷分四大题。
满分:150分。
考试时间:150分钟)注意事项:1.本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
答卷前,考生务必将自己的班级、姓名、座号、考场、考场座位号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷上无效。
第Ⅰ卷阅读题一、现代文阅读(35分)(一)论述类文本阅读(9分,每小题3分)阅读下面的文字,完成1~3题。
乐府诗在入唐以前已存在两个传统,一是上承“诗教”风刺一面的汉魏传统,二是以艳歌艳词为主的六朝传统。
初唐乐府沿袭齐梁绮靡的路子,内容不出白氏所批评的“赞君美”或“悦君意”。
“初唐四杰”的乐府虽体现闻一多先生所谓“由宫廷走到市井”“由台阁移到江山和塞漠”的倾向,但现实的针对性不强。
盛唐以边塞为题材的乐府诗,更多地歌颂盛唐的武功气象。
中唐以后,张籍、王建、元稹、白居易和刘禹锡集中创作乐府,试图在理念的层次上直接继承《诗经》的“风刺”传统,甚至否定汉乐府的价值,但选择以“乐府”而非其他诗体干预政治,还是反映出他们对于汉乐府观风知俗观念的继承。
不仅如此,中唐乐府诗人吸收了六朝的部分传统,展现出对于地方风土风俗的书写兴趣。
中唐大量出现表现地方风土或风俗的乐府,与中唐观风观念的转变关系密切。
初唐、盛唐之观风俗以政治治理为中心;另一方面,更是要通过礼乐教化来“移风易俗”。
但安史之乱后,中唐人不再视地方风俗为负面的无条件改造对象。
高郢《礼部试策五道》指出“然为政之道,当因人所利而利之,故修其教不易其俗,齐其政不易其宜”。
欧阳詹《鲁山令李胄三月三日宴僚吏序》说得更加清楚:“一方不同教化,恐他邑之欢乐此辰,不得似公之邑也。
”同时,“采风”或“采诗”的理想被中唐诗人不断提出。
但其“采诗”与汉人有异,所采并不是真正来自民间,而是从士大夫的创作中收集而得,与其说是“采诗”,不如说是“献诗”。
白居易和刘禹锡是中唐乐府大家,白氏真正主张的是“采诗以补察时政”,新乐府如《上阳白发人》《卖炭翁》《道州民》都已涉及唐世风俗的叙写。

福建省厦门双十中学2014届高三热身考试理科综合能力测试试卷本试卷分第I卷(选择题)和第II卷。
第I卷为必考题,第II卷包括必考题和选考题两部分。
本试卷共12页,满分300分,考试时间150分钟。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上。
2.考生作答时,请将答案答在答题卡上,在本试卷上答题无效;按照题号在各题的答题区域内作答,超出答题区域书写的答案无效。
3.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
4.做选考题时,考生按照题目要求作答,并用2B铅笔在答题卡上把所选题目对应的题号涂黑。
5.保持答题卡卡面清洁,不折叠,不破损;考试结束后,将答题卡交回。
相对原子质量:H-1、C-12、N-14、O-16、S-16、K-39第Ⅰ卷(选择题共108分)本卷共18小题,每小题6分,共108分。
在每小题给出的四个选项中,只有一个选项符合题目要求。
1.根据图示坐标曲线,下列描述正确的是A.若该曲线表示紫色洋葱鳞片叶细胞液泡体积的大小变化,则CD段表示该细胞吸水能力逐渐增强B.若该曲线代表密闭温室中的CO2浓度在一天中的变化情况,则温室中植物光合作用开始于B点C.若该曲线表示在温度交替变化的环境中健康人的皮肤血流量变化,则AB段血液中明显增多的激素是肾上腺素和甲状腺激素D.若该曲线表示正常人进食后的血糖浓度变化,则CD段血液中胰高血糖素含量上升2.右图为研究渗透作用的实验装置,漏斗内溶液(S1)和漏斗外溶液(S2),漏斗内外起始液面一致。
渗透平衡时的液面差为△h。
下列有关分析正确的是A.若S1 、S2分别是不同浓度的蔗糖溶液,渗透平衡时的液面差为△h,S1浓度大于S2的浓度B.若S1 、S2分别是不同浓度的蔗糖溶液,渗透平衡时的液面差为△h,S1浓度等于S2的浓度C.若S1 、S2分别是不同浓度的KNO3溶液,渗透平衡时的液面差为△h,S1浓度大于S2的浓度D.若S1 、S2分别是不同浓度的KNO3溶液,渗透平衡时的液面差为△h,S1浓度等于S2的浓度3.狗的皮毛颜色是由两对基因(A,a和B,b)控制的,共有四种表现型:黑色(A_B_)、褐色(aaB_)、红色(A_bb)和黄色(aabb),右图为黑色狗的细胞(仅表示出存在相关基因的染色体)。
2014年厦门双十中学高三适应性考试文科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第40~42题为选考题,其他题为必考题。
第Ⅰ卷(共144分)本卷共36小题,每小题4分,共144分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
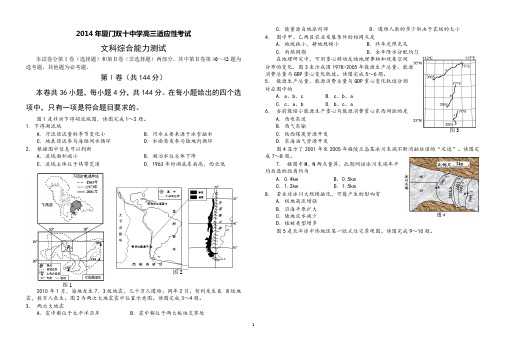
图1是非洲乍得胡流域图,读图完成1~2题。
1. 乍得湖流域A. 河流径流量的季节变化小 B.河水主要来源于冰雪融水C.地表径流参与海陆间水循环 D.水面蒸发参与陆地内循环2.根据图中信息可以判断A.流域面积减小 B.湖泊水位总体下降C.流域主体位于热带荒漠 D.1963年时湖底东南高,西北低2010年1月,海地发生7.3级地震,几十万人遇难;同年2月,智利发生8.8级地震,数百人丧生。
图2为两次大地震震中位置示意图。
读图完成3~4题。
3.两次大地震A.震中都位于太平洋沿岸 B.震中都位于两大板块交界处C.能量源自地球内部 D.遇难人数的多少取决于震级的大小4.图中甲、乙两区农业发展条件的相同点是A.地域狭小,耕地规模小 B.终年光照充足C.雨热同期 D.全年降水分配均匀在地理研究中,可用重心移动反映地理事物和现象空间分布的变化,图3表示我国1978-2005年能源生产总量、能源消费总量与GDP重心变化轨迹。
读图完成5~6题。
5.能源生产总量、能源消费总量与GDP重心变化轨迹分别对应图中的A. a、b、cB. c、b、aC. c、a、bD. b、c、a6.当前能缩小能源生产重心与能源消费重心东西间距的是A. 西电东送B. 西气东输C. 陕西煤炭资源开发D. 东海油气资源开发图4显示了2001年至2005年格陵兰岛某冰川末端不断消融后退的“足迹”。
读图完成7~8题。
7.据图中M、N两点量算,此期间该冰川末端年平均后退的距离约为A.0.4km B.0.5kmC.1.2km D.1.5km8.若全球冰川大规模融化,可能产生的影响有A.极地高压增强B.沿海平原扩大C.陆地淡水减少D.植被类型增多图5是北半球中纬地区某一欧式住宅景观图。

厦门双十中学2014届语文5月热身考本试卷分五大题,共10页。
满分150分,考试时间150分钟。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上。
2.考生作答时,请将答案写在答题卡上,在本试卷上答题无效。
按照题号在各题的答题区域内作答,超出答题区域书写的答案无效。
3.答题使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
4.做选考题时,考生按照题目要求作答,并在答题卡上填写所选题目的序号。
5.保持答题卡卡面清洁,不折叠,不破损。
考试结束后,将本试卷和答题卡一并交回。
一、古代诗文阅读(27分)(一)默写常见的名句名篇(6分)1.补写出下列名句名篇中的空缺部分。
(6分)⑴锲而不舍,。
(《荀子·劝学》)⑵,闻道龙标过五溪。
(李白《闻王昌龄左迁龙标遥有此寄》)⑶,抱明月而长终。
(苏轼《赤壁赋》)⑷潦水尽而寒潭清,。
(王勃《滕王阁序》)⑸外无期功强近之亲,。
(李密《陈情表》)⑹箫鼓追随春社近,。
(陆游《游山西村》)㈡文言文阅读(15分)阅读下面的文言文,完成2-5题。
养狸述(唐)舒元舆野禽兽可驯养而有裨于人者,吾得之于狸。
狸之性,憎鼠而喜爱①。
其体趫②、其文班。
予爱其能息鼠窃,近乎正且勇。
尝观虞人(掌管山泽的官吏)生致.者,因得请归,致新昌里客舍。
舍之初未为某居时,曾为富商家廪,墉堵地面,甚足鼠窍,日有鼠络绎然。
某既居,果遭其暴.耗。
常白日为群,虽敲拍叱吓,略不畏忌。
或暂黾侻跧③缩,须臾复来,日数十度。
其穿巾孔.箱之患,继晷而有。
昼或出游,及归,其什器服物,悉已破碎。
若夜时长留④续晨,与役夫更吻驱呵,甚累神抱。
或知之,借椟以收拾衣服,未顷,则椟又孔矣。
予心深闷,当其意欲掘地诛剪,始二三十日间,未果。
颇患之,若抱痒疾。
自获此狸,尝阖关实窦,纵于室中,潜伺之。
见轩首引鼻,似有鼠气,则凝蹲不动。
斯须,果有鼠数十辈接尾而出,狸忽跃起,张爪呀牙,划泄怒声,鼠党帖伏不敢窜。

2014年厦门双十中学高三年第八次适应性考试卷文科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第40~42题为选考题,其他题为必考题。
第Ⅰ卷(共144分)本卷共36小题,每小题4分,共144分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
图1是非洲乍得胡流域图,读图完成1~2题。
1. 乍得湖流域A. 河流径流量的季节变化小 B .河水主要来源于冰雪融水 C .地表径流参与海陆间水循环 D .水面蒸发参与陆地内循环 2. 根据图中信息可以判断A .流域面积减小B .湖泊水位总体下降C .流域主体位于热带荒漠D .1963年时湖底东南高,西北低图12010年1月,海地发生7.3级地震,几十万人遇难;同年2月,智利发生8.8级地震,数百人丧生。
图2为两次大地震震中位置示意图。
读图完成3~4题。
3. 两次大地震A .震中都位于太平洋沿岸B .震中都位于两大板块交界处C .能量源自地球内部D .遇难人数的多少取决于震级的大小 4. 图中甲、乙两区农业发展条件的相同点是A .地域狭小,耕地规模小B .终年光照充足C .雨热同期D .全年降水分配均匀在地理研究中,可用重心移动反映地理事物和现象空间分布的变化,图3表示我国1978-2005年能源生产总量、能源消费总量与GDP 重心变化轨迹。
读图完成5~6题。
5. 能源生产总量、能源消费总量与GDP 重心变化轨迹分别 对应图中的A. a 、b 、cB. c 、b 、aC. c 、a 、bD. b 、c 、a6. 当前能缩小能源生产重心与能源消费重心东西间距的是A. 西电东送B. 西气东输C. 陕西煤炭资源开发D. 东海油气资源开发图4显示了2001年至2005年格陵兰岛某冰川末端不断消融后退的“足迹”。
读图完成7~8题。
图2图37.据图中M、N两点量算,此期间该冰川末端年平均后退的距离约为A.0.4km B.0.5km C.1.2km D.1.5km8.若全球冰川大规模融化,可能产生的影响有A.极地高压增强 B.沿海平原扩大 C.陆地淡水减少 D.植被类型增多图5是北半球中纬地区某一欧式住宅景观图。

第4题图福建省厦门双十中学2014届高三热身考数学〔文〕试卷第1卷〔选择题共60分〕一、选择题:本大题共12小题,每一小题5分,总分为60分.在每一小题给出的四个选项中,只有一项为哪一项符合题目要求的.1.集合{}12,A x x x Z =-≤≤∈,集合{}420,,=B ,如此B A ⋃ 等于 A .{}4,2,1,0,1- B .{}4,2,0,1- C .{}420,,D .{}4210,,, 2.在"3""23sin ",π>∠>∆A A ABC 是中 的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件3.函数22 (0),()log (0),x x f x x x ⎧<=⎨>⎩假设直线y m =与函数()f x 的图象有两个不同的交点,如此实数m 的取值范围是A. R m ∈B. 1>mC. 0>mD. 10<<m 4.某程序框图如下列图,该程序运行后输出的x 值是A .3B .4C .6D .85.双曲线C :22x a -22y b =1的焦距为10 ,点P 〔2,1〕在C 的渐近线上,如此C 的方程为A .220x -25y =1 B.25x -220y =1 C.280x -220y =1 D.220x -280y =16.设1122(,),(,),...,(,)n n x y x y x y ,是变量x 和y 的n 个样本点,直线l 是由这些样本点通过最小二乘法得到的线性回归方程(如图〕,以下结论中正确的答案是〔 〕 A .x 和y 正相关B .x 和y 的相关系数为直线l 的斜率C .x 和y 的相关系数在-1到0之间D .当n 为偶数时,分布在l 两侧的样本点的个数一定一样7.如图,BC 是单位圆A 的一条直径, F 是线段AB 上的点,且2BF FA =, 假设DE 是圆A 中绕圆心A 运动的一条直径,如此FE FD •的值是〔 〕 A.34-B. 89-C. 14- D. 不确定 8.假设正数x ,y 满足x+3y=5xy ,如此3x+4y 的最小值是 A.245 B.285C.5D.6 9.函数()sin()f x A x ωϕ=+〔其中0,||2A πϕ><〕的图象如下列图,为了得到x x g 2sin )(=的图像,如此只需将()f x 的图像A .向右平移6π个长度单位 B .向右平移12π个长度单位C .向左平移6π个长度单位 D .向左平移12π个长度单位10.函数()xx ex f -=sin ,有如下四个结论:①是奇函数 ②是偶函数 ③在R 上是增函数 ④在R 上是减函数 其中正确的个数为 〔 〕A .0B .1C .2D .311.假设x,y 满足y ax z y x y x y x 2,22,1,1+=⎪⎩⎪⎨⎧≤--≥-≥+且仅在点〔1,0〕处取得最小值,如此实数a 的取值范围是A .(]0,4-∈aB . [)2,0∈aC .(4,2)a ∈-D 。
C第4题图福建省厦门双十中学2014届高三热身考数学(文)试卷第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}12,A x x x Z =-≤≤∈,集合{}420,,=B ,则B A ⋃ 等于 A .{}4,2,1,0,1- B .{}4,2,0,1- C .{}420,, D .{}4210,,,2.在"3""23sin ",π>∠>∆A A ABC 是中 的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3. 已知函数22 (0),()log (0),x x f x x x ⎧<=⎨>⎩若直线y m =与函数()f x 的图象有两个不同的交点,则实数m 的取值范围是A. R m ∈B. 1>mC. 0>mD. 10<<m 4.某程序框图如图所示,该程序运行后输出的x 值是 A .3 B .4 C .6 D .85.已知双曲线C :22x a -22y b=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C 的方程为A .220x -25y =1 B.25x -220y =1 C.280x -220y =1 D.220x -280y =16.设1122(,),(,),...,(,)n n x y x y x y ,是变量x 和y 的n个样本点,直线l 是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( ) A .x 和y 正相关B .x 和y 的相关系数为直线l 的斜率C .x 和y 的相关系数在-1到0之间D .当n 为偶数时,分布在l 两侧的样本点的个数一定相同7. 如图,BC 是单位圆A 的一条直径, F 是线段AB 上的点,且2BF FA =, 若DE 是圆A 中绕圆心A 运动的一条直径,则∙的值是( )A.34-B. 89-C. 14- D. 不确定 8.若正数x ,y 满足x+3y=5xy ,则3x+4y 的最小值是 A.245 B. 285C.5D.6 9.函数()s i n()f x A x ωϕ=+(其中0,||2A πϕ><)的图象如图所示,为了得到x x g 2sin )(=的图像,则只需将()f x 的图像A .向右平移6π个长度单位 B .向右平移12π个长度单位C .向左平移6π个长度单位 D .向左平移12π个长度单位10.已知函数()x x e x f -=sin ,有如下四个结论:①是奇函数 ②是偶函数 ③在R 上是增函数 ④在R 上是减函数其中正确的个数为 ( )A .0B .1C .2D .311.若x,y 满足y ax z y x y x y x 2,22,1,1+=⎪⎩⎪⎨⎧≤--≥-≥+且仅在点(1,0)处取得最小值,则实数a 的取值范围是A .(]0,4-∈aB . [)2,0∈aC .(4,2)a ∈-D 。
福建省厦门双十中学2014届高三热身考试地理本试卷分第1卷〔选择题〕和第2卷〔非选择题〕两局部,其中第2卷第40~42题为选考题,其他题为必考题。
第1卷〔共144分〕本卷共36小题,每一小题4分,共144分。
在每一小题给出的四个选项中,只有一项为哪一项符合题目要求的。
2014年3月24日当地时间22时马来西亚总理纳吉布·拉扎克宣布,根据最新收到的卫星分析数据,可以判定马来西亚航空公司MH370航班在印度洋南部海域(42°S, 92°E) “终结〞。
此时该海域风大浪高,多恶劣天气,给海上搜救带来极大困难。
据此完成1~3题。
1.获取卫星分析数据运用的地理信息技术是A.RS B.RS和GPS C.GPS和GIS D.RS和GIS2.该海域此时风大浪高的主要原因是A.地处热带,海水温度高 B.温带海域,西风强盛C.副高控制,上升气流强D.大洋中部,洋流强大3.该海域此时多恶劣天气的主要原因是A.盛行西南风B.暖湿气团影响强烈C.盛行东北风D.温带气旋活动频繁图1示意南半球某区域农事安排。
该区域农场内一般划分为假设干个区域,分别为小麦地、图1放牧地、休耕地等,在土地上交替种植小麦、牧草或休耕。
读图完成4~5题。
4.该区域的农业地域类型最有可能是A.种植园农业 B.商品谷物农业C.混合农业D.大牧场放牧业5.在土地上交替种植小麦、牧草或休耕的最主要目的是A.合理有效安排农事活动B.更好地适应市场需求C.便于农民开拓销售渠道D.充分保持麦田的肥力表1示意中纬地区某流域气候资料(流域内气候差异较小)。
读表完成6~7题。
表16. 有关该流域气候特征描述正确的答案是A. 终年暖湿B. 气温年较差大C. 海洋性强D. 降水年变化小7. 该河最大流量出现在A. 春季B. 夏季C. 秋季D. 冬季最大可能蒸发量是指地表在水分充足的条件下产生的最大蒸发量。
图2示意某地1961-1990年间相关统计资料,读图完成8~9题。
某某省某某双十中学2014届高三热身考试历史试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第40~42题为选考题,其他题为必考题。
第Ⅰ卷(共144分)本卷共36小题,每小题4分,共144分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
13. 唐朝的三省制与美国三权分立体制有着根本的区别。
因为A.三个部门没有相互监督的职能B.三省不是独立行使职权的部门C.三省之中没有管司法的部门D.三省的长官不是选举产生的14. 鲁迅说:“明之中叶,即嘉靖前后,小说出现得很多,其中有两大主流:一、讲神魔之争的;二、讲世情的。
……当神魔小说盛行的时候,讲世情的小说,也就起来了。
”下列作品符合该时期的有A. B. C. D.15. 列宁在评论近代中国的某一事件时指出,标榜“自由”、“某某”、“某某”的欧洲资产阶级国家,并没有支持中国的革命运动;相反,这一运动激起了他们“掠夺中国”的欲望,为此还与中国的落后势力“实行联盟”。
列宁所指的事件是A. 义和团运动B. 辛亥革命C. 五四运动D. 国民革命图4 16.图4是某学者概括的近现代中国思想发展历程思维导图,这说明近现代中国思想发展历程A.是一个不断碰撞分化与融合的过程 B.是一个东学西渐的过程C.是一个不断回归传统儒学的过程 D.是一个从器物到制度到文化的过程17. 某某会议是中国共产党历史上生死攸关的转折点。
此后中共进一步成熟,表现在A.从理论上和实践上开始探索中国革命的正确道路B.依据中国社会性质提出了正确的某某革命纲领C.反“围剿”失利后,排除“左”倾错误的干扰开始长征D.根据社会主要矛盾的变化,正确处理国共两党关系18. 为照顾那些仍未跟上对外政策变化的顽固分子,《纽约时报》的封面用红字印着“红色中国”,但也用小号字提到了人民某某国;封底是赖思顿(《纽约时报》副社长)和周恩来并肩而坐,正在商谈政策。
这种情况最早可能发生在A.1949年 B.1971年 C.1972年 D.1979年19. 在古代雅典,Asion一词是指那些仅在身体意义上属于这个城邦,但被排除在公民组织之外的自由民。
【全国名校】2014届福建厦门双十中学高三热身考试生物卷学校:___________姓名:___________班级:___________考号:___________ 一、单选题(本大题共5小题,共5.0分)1.根据图示坐标曲线,下列描述正确的是A.若该曲线表示紫色洋葱鳞片叶细胞液泡体积的大小变化,则CD段表示该细胞吸水能力逐渐增强B.若该曲线代表密闭温室中的CO2浓度在一天中的变化情况,则温室中植物光合作用开始于B点C.若该曲线表示在温度交替变化的环境中健康人的皮肤血流量变化,则AB段血液中明显增多的激素是肾上腺素和甲状腺激素D.若该曲线表示正常人进食后的血糖浓度变化,则CD段血液中胰高血糖素含量上升【答案】D【解析】试题分析:植物细胞的吸水能力与细胞液的浓度有关,BC段液泡的体积变小,说明细胞失水,C点时失水最多,细胞液浓度最大,吸水能力最强,故A错误;若曲线表示密闭温室中二氧化碳浓度的变化,B点时,二氧化碳浓度不变,此时光合速率等于呼吸速率,故光合作用开始于B点之前,故B错误;若该曲线表示温度交替变化的环境皮肤血流量的变化,AB段皮肤血流量增多,说明外界为炎热环境下,肾上腺素和甲状腺激素分泌减少,故C错误;若该曲线表示血糖浓度的变化曲线,C点血糖浓度偏低,故胰高血糖素分泌增加,故D正确。
考点:本题考查植物细胞的吸水与失水、光合作用、体温调节和血糖调节的有关知识,意在考查考生识图能力和理解所学知识的要点,把握知识间的内在联系的能力。
2.下图为研究渗透作用的实验装置,漏斗内溶液(S1)和漏斗外溶液(S2),漏斗内外起始液面一致。
渗透平衡时的液面差为△h。
下列有关分析正确的是A.若S1 、S2分别是不同浓度的蔗糖溶液,渗透平衡时的液面差为△h,S1浓度大于S2B.若S1 、S2分别是不同浓度的蔗糖溶液,渗透平衡时的液面差为△h,S1浓度等于S2的浓度C.若S1 、S2分别是不同浓度的KNO3溶液,渗透平衡时的液面差为△h,S1浓度大于S2的浓度D.若S1 、S2分别是不同浓度的KNO3溶液,渗透平衡时的液面差为△h,S1浓度等于S2的浓度【答案】A【解析】试题分析:由于半透膜允许离子和水分子自由通过,但不允许蔗糖分子通过,因此若S1、S2分别是不同浓度的蔗糖溶液,由于漏斗内液面上升,因此漏斗内浓度大,即S1浓度大于S2浓度,故A正确,B错误;由于半透膜允许离子自由通过,S1、S2分别是不同浓度的KNO3溶液,平衡时漏斗内外液面高度相等,故CD错误。
C第4题图福建省厦门双十中学2014届高三热身考数学(文)试卷第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}12,A x x x Z =-≤≤∈,集合{}420,,=B ,则B A ⋃ 等于 A .{}4,2,1,0,1- B .{}4,2,0,1- C .{}420,, D .{}4210,,, 2.在"3""23sin ",π>∠>∆A A ABC 是中 的 A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件3. 已知函数22 (0),()log (0),x x f x x x ⎧<=⎨>⎩若直线y m =与函数()f x 的图象有两个不同的交点,则实数m 的取值范围是A. R m ∈B. 1>mC. 0>mD. 10<<m 4.某程序框图如图所示,该程序运行后输出的x 值是 A .3 B .4 C .6 D .85.已知双曲线C :22x a -22yb=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C 的方程为 A .220x -25y =1 B.25x -220y =1 C.280x -220y =1 D.220x -280y =16.设1122(,),(,),...,(,)n n x y x y x y ,是变量x 和y 的n 个样本点,直线l 是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( )A .x 和y 正相关B .x 和y 的相关系数为直线l 的斜率C .x 和y 的相关系数在-1到0之间D .当n 为偶数时,分布在l 两侧的样本点的个数一定相同 7. 如图,BC 是单位圆A 的一条直径, F 是线段AB 上的点,且2BF FA =, 若DE 是圆A 中绕圆心A 运动的一条直径,则∙的值是( )A.34-B. 89-C. 14- D. 不确定8.若正数x ,y 满足x+3y=5xy ,则3x+4y 的最小值是A. 245B. 285C.5D.69.函数()sin()f x A x ωϕ=+(其中0,||2A πϕ><)的图象如图所示,为了得到x x g 2sin )(=的图像,则只需将()f x 的图像A .向右平移6π个长度单位 B .向右平移12π个长度单位C .向左平移6π个长度单位 D .向左平移12π个长度单位10.已知函数()xx e x f -=sin ,有如下四个结论:①是奇函数 ②是偶函数 ③在R 上是增函数 ④在R 上是减函数 其中正确的个数为 ( )A .0B .1C .2D .311.若x,y 满足y ax z y x y x y x 2,22,1,1+=⎪⎩⎪⎨⎧≤--≥-≥+且仅在点(1,0)处取得最小值,则实数a 的取值范围是A .(]0,4-∈aB . [)2,0∈aC .(4,2)a ∈-D 。
()()2,00,4⋃-∈a12.已知集合M 是满足下列性质的函数()f x 的集合:存在非零常数k ,对定义域中的任意x ,等式()f kx =2k+()f x 恒成立.现有两个函数:()()0f x ax b a =+≠,()2log g x x =,则函数()f x 、()g x 与集合M 的关系为A .()()M x g M x f ∈∈,B .()()M x g M x f ∈∉,C .()()M x g M x f ∉∈,D .()()M x g M x f ∉∉,第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置.13.如果mi i+=-112(R m ∈,i 表示虚数单位),那么=m 14. 在半径为1的圆内一条直径AB 上任取一点M ,过点M 作垂直于直径AB 的弦,则弦长大于3的概率是 .15.已知抛物线y 2=2px(p >0)有一个内接直角三角形,直角顶点在原点,斜边长为213,一直角边的方程是y=2x,则抛物线的方程为16.已知函数)(x f 是定义域为R ,且,x y R ∀∈∈都有:()()()f x y xf y yf x ⋅=+,且(2)2f =,若数列{}n a 满足()*(2)n n f a n N n-=∈,求数列{a n }的通项公式n a =三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤. 17.(本小题12分)某校高一新生1000人中,来自A, B ,C ,D ,E 五个不同的初中校,现从中随机抽取20人,对其所在初中校进行统计分析,得到频率分布表如下:初中校A B C D E频率0.05 m 0.15 0.35 n(Ⅰ)在抽取的20个同学中,来自E 学校的为2人,求m ,n 的值;(Ⅱ)在(Ⅰ)的条件下,从来自C 和E 两学校的同学中任取2人,求抽取的2个人来自不同学校的概率. 18.(本小题满分12分) 已知等差数列{a n }中,其前n 项和c n S n +=2(其中c 为常数),(1)求{a n }的通项公式;(2)设{}n n b a b +=,11是公比为2a 等比数列,求数列{b n }的前n 项和n T19.(本小题满分12分)在直角坐标系xOy 中,若角α的始边为x 轴的非负半轴,终边为射线l :y=x (x ≥0).(1)求sin(2)6πα+的值;(2)若点P ,Q 分别是角α始边、终边上的动点,且PQ =4,求△POQ 面积最大时,点P ,Q 的坐标. 20.(本小题满分12分)已知长方体1111ABCD A B C D -,其中2AB BC ==,过11A C B 、、三点的的平面截去长方体的一个角后.得到如图所示的,且这个几何体的体积为403. (1)求几何体111ABCD AC D -的表面积;(2)在线段1BC 上是否存在点P ,使直线1A P 与1C D 垂直, 如果存在,求线段1A P 的长,如果不存在,请说明理由.21. (本小题满分12分)已知椭圆C:22221x y a b+=( 0a b >>)的离心率为21,点(1,32)在椭圆C 上.(Ⅰ)求椭圆C 的方程;(Ⅱ) 若椭圆C 的两条切线交于点M (4,t ),其中t R ∈,切点分别是A 、B ,试利用结论:在椭圆22221x y a b+=上的点(00,x y )处的椭圆切线方程是00221x x y ya b+=,证明直线AB 恒过椭圆的右焦点2F ; (Ⅲ)试探究2211||||AF BF +的值是否恒为常数,若是,求出此常数;若不是,请说明理由. 22.(本小题满分14分) 已知函数()21ax b f x x +=+(其中常数,a b R ∈),()2sin g x x x π=- ( π是圆周率) .(Ⅰ)当1=a 时,若函数()f x 是奇函数,求()f x 的极值点; (Ⅱ)求函数()f x 的单调递增区间; (Ⅲ)当0,,2b a ππ⎛⎤=∈⎥⎝⎦时,求函数()g x 在[]0,a 上的最小值()h a ,并探索:是否存在满足条件的实数a ,使得对任意的x R ∈,()()f x h a >恒成立.福建省厦门双十中学2014届高三热身考数学(文)试卷答案(2014.05.28)一、答案:AADDA CBCAB CB1A 【解析】由已知,{}2,1,0,1-=A ,{}4,2,1,0,1-=⋃B A ,选A 2A 【解析】ABC ∆中,⎪⎭⎫⎝⎛∈⇒>32,323sin ππA A ,故选A 3D 【解析】由图象可知4D 【解析】3,223242,431,1,12==⨯+=→==+=→==k S k S S k 82,4,10010333223==∴=>=⨯+=→k x k S ,选D5A 【解析】设双曲线C :22x a -22y b =1的半焦距为c ,则210,5c c ==.又 C 的渐近线为by x a=±,点P (2,1)在C 的渐近线上,得2a b =.又222c a b =+,a ∴==∴C 的方程为220x -25y =1.6C 【解析】x 和y 的相关系数()1,1-∈r ,负相关时为负,故选C7B 【解析】法一:向量分解法()()()()9822-=-=-∙+=+∙+=∙ 法二: 特殊法:让DE 与BC 重合,则有98180cos 3432-=⋅⋅=∙︒ 8.C 【解析】x+3y=5xy ,135y x+=, 113131213(34)()()555x y x y y x y x +⋅+=++≥1132555⨯=. 9. A 【解析】由已知,,1=A 2,,431274=∴=∴=-=ωππππT T ,127π=x 时,231272πϕπϕω=+⨯=+x , 3πϕ=∴,()⎪⎭⎫ ⎝⎛+=∴32sin πx x f ,只需用6π-x 代入可得x x g 2sin )(=的图像,故选A10. B 【解析】定义域为R ,()10=f ,故①错;()ππe f =-,()ee f 1==-ππ,故②错;设()()01cos ,sin ≤-='∴-=x x u x x x u ,故(),sin x x x u -=在R 上是减函数,()x x e x f -=sin 在R 上是减函数,故④正确,③错误,故选B11. C 【解析】画出区域图,可知当0=a 时,y z 2=,即z y 21=,符合题意;当0>a 时,z x a y 212+-=,斜率12->-a,即20<<a 时符合题意;当0<a 时,z x a y 212+-=,斜率22<-a,即04<<-a 时符合题意; 综上,(4,2)a ∈-12. B 【解析】(1)若()f x =ax +b ∈M ,则存在非零常数k ,对任意x ∈D 均有()f kx =akx +b =2k+()f x ,即a (k -1)x =2k恒成立,得100k k -=⎧⎨=⎩,,无解,所以()f x ∉M .(2)2log ()kx =2k +2log x ,则2log k =2k,k =4,k =2时等式恒成立,所以()f x =2log x ∈M .二、填空题: 13.1【解析】111,112=⇒+=+⇒+=-m mi i mi i14. 21【解析】当截得的弦长等于3时,半弦长等于2,因为半径为1,12OM =,故符合条件的M 应满足12OM ≤,故1212212P ⨯==⨯ 15 y 2=58x.【解析】因为一直角边的方程是y=2x,所以另一直角边的方程是y=-21x.由⎪⎩⎪⎨⎧==px y xy 222,解得⎪⎩⎪⎨⎧==p y p x 2,或⎩⎨⎧==00y x (舍去), 由⎪⎩⎪⎨⎧=-=pxy xy 2212,解得⎩⎨⎧-==p y p x 48,或⎩⎨⎧==00y x (舍去),∴三角形的另两个顶点为⎪⎭⎫ ⎝⎛p p ,2和(8p,-4p ).∴22)4()82(p p p p ++-=213.解得p=54,故所求抛物线的方程为y 2=58x.16.12n-【解析】因为对任意,x y R ∈,()()()f x y xf y yf x ⋅=+成立,令1x y ==可得()10f =, 令1,22x y ==可得()()1112222f f f ⎛⎫=+ ⎪⎝⎭,得1122f ⎛⎫=- ⎪⎝⎭,()()11122211n n n f f a n n --++⎛⎫⨯ ⎪⎝⎭∴==++()111222222211n n n nna f f n n ---⎛⎫+-⨯+ ⎪⎝⎭==++ 得()11212n n n n a na ++=-+ 得 ()111221n nn n n a n a +++-=- 所以数列{}2nn n a 是等差数列,公差为1-,首项为121a =-,故2n n n a n =-,得12n n a =-法二:求出1122f ⎛⎫=- ⎪⎝⎭,得211-=a ;令41,2==y x 得2141-=⎪⎭⎫ ⎝⎛f ,412-=a ;令81,2==y x ,8381-=⎪⎭⎫⎝⎛f ,813-=a ……归纳出12n n a =-三.解答题17【解析】:(1)由频率分布表得:45.0,135.015.005.0=+∴=++++n m n m ----------------2分由抽取的20人中,来自E 学校恰有2个人,则35.01.045.0,1.0202=-=∴==m n --------------------5分(2)由(1)得来自C 学校有3人,记作321,,x x x ,来自E 学校的有2个,记作21,y y从21321,,,,y y x x x 中任取2个,有),(),,(),,(),,)(,(),,(),,(22123221113121y x y x x x y x y x x x x x),(),,(),,(212313y y y x y x 共10种 ------------------------------------------------------------------------8分记事件A 为“从21321,,,,y y x x x 中任取2个人,来自不同学校”,则A 包含的基本事件是),)(,(),,(),,)(,)(,(231322122111y x y x y x y x y x y x 共6个 ---------------------------------------------10分所求概率53106)(==A P ------------------------------------------------------------------------------------------12分 18.【解析】:(1) ,111c S a +== ,3122=-=S S a 5233=-=S S a -----------2分 因为等差数列{a n },所以3122a a a += 得0=c -------------------------------------4分211==∴d a 12-=n a n -----------------------------------6分(2) 32=a ,211=+b a 132-⨯=+∴n n n b a ------------------------------8分n n n a b -⨯=∴-132-----------------------------------------------9分()()1331312221--=+++---=∴n a a a S n n nn -------------------12分19. 【解析】:19:(1 )由射线l的方程为y =,可得31cos ,322sin ==αα,----------------------4分7sin(2)sin 2cos cos 2sin 66618πππααα+=+=-故.-----------6分(2) 设()()()0,022,,0,>>b a b b Q a P在POQ ∆中, 因为()168222=+-=b b a PQ ,---------------------------------------------7分即ab ab ab ab b a 426291622=-≥-+=,所以ab ≤4.--------------------------------8分∴POQ S ∆≤b a 3=,即332,32==b a 取得等号.--------------10分 所以POQ ∆面积最大时,点,P Q 的坐标分别为()⎪⎪⎭⎫⎝⎛364,332,0,32Q P .--------------12分20.【解析】:(1)1111111111ABCD AC D ABCD A B C D B A B C V V V ---=- 1111110402222,3233AA AA AA =⨯⨯-⨯⨯⨯⨯==14AA ∴=.------------------------------------------------------3分22,521111===C A B C B A ,设11C A 的中点H ,所以62311=∴=∆B C A S BH ---------------------------5分∴表面积3662483=+++⨯=S ----------------------6分(2)在平面11CC D D 中作11D Q C D ⊥交1CC 于Q ,过Q 作//QP CB 交1BC 于点P ,则11A P C D ⊥.----------------------------------------7分因为1111111111,,A D CC D D C D CC D D C D A D ⊥⊂∴⊥平面平面,而1111//,//,//QP CB CB A D QP A D ∴, 又1111,A D D Q D C D A PQC =∴⊥平面,111PQCD A D C 平面⊥∴且11111,A P A PQC A P C D ⊂∴⊥平面.…………………9分 11D C Q ∆∽A 1DD 1C 1 ACPQ B11111111,,1,//,42C QD C Rt C CD C Q PQ BC PQ BC CD C C∆∴=∴=∴==又. 11A PQD 四边形为直角梯形,且高112D Q A P ===……12分 21【解析】: (Ⅰ)设椭圆C 的方程为22221x y a b +=(0a b >>) ,431222=-=e ab ①点(1,32)在椭圆C 上,221914a b+=②,由①②得:224,3a b ==∴椭圆C 的方程为22143x y +=, ……………… 4分 (Ⅱ)设切点坐标11(,)A x y ,22(,)B x y ,则切线方程分别为11143x x y y +=,22143x x y y+=. 又两条切线交于点M(4,t ),即1113t x y +=,2213tx y += 即点A 、B 的坐标都适合方程13tx y +=,显然对任意实数t ,点(1,0)都适合这个方程, 故直线AB 恒过椭圆的右焦点2F . ……………… 8分 (Ⅲ)将直线AB 的方程13tx y =-+,代入椭圆方程,得 223(1)41203t y y -++-=,即22(4)2903t y ty +--=所以122612t y y t +=+,1222712y y t =-+……………… 10分 不妨设120,0y y ><,21||AF y ==,同理22||BF y =所以2211||||AF BF +21121211()y y y y y y --==1243= 所以2211||||AF BF +的值恒为常数43.----------------------------------12分22【解析】:解:(Ⅰ)函数()f x 是奇函数,∴对x R ∈,()()f x f x -=-成立,得2222,00111x b x b bb x x x -++=-∴=⇒=+++(利用奇函数,得()00f b ==也给1分)-------1分 ()2,1x f x x ∴=+得()()()2222222121,11x x x f x x x +--+'==++--------------------------------------------------2分从()0f x '=得21,1x x =∴=±经检验1x =±是函数()f x 的极值点. --------------------------------------------------------------------------4分 (Ⅱ)()21ax bf x x +=+,()()()()()22222212211a x x axb ax bx a f x x x +-+--+'∴==++, 从()2020f x ax bx a '>⇒--+>,得220ax bx a +-<①0,0a b ==时,()0f x =,不存在单调递增区间;②0,0a b =≠时,<ⅰ>0b >时,0x <,单调递增区间为(),0-∞;-----------------------------------5分 <ⅱ>0b <时,0x >,单调递增区间为()0,+∞;-----------------------------------6分③0a >,方程220ax bx a +-=的判别式22440b a ∆=+>,两根x ==单调递增区间为⎝⎭---------------------------------------------------------7分④0a <时,单调递增区间为⎛-∞ ⎝⎭和⎫+∞⎪⎪⎝⎭--------------------------8分 (Ⅲ)()2cos g x x π'=-,当[]0,x a ∈时,令()0g x '=得02cos x π=,其中00,2x π⎛⎫∈ ⎪⎝⎭当x∴函数()g x 在0,a 上的最小值为0g 与g a 的较小者()00g =,()02g a g π⎛⎫<= ⎪⎝⎭,()()h a g a ∴=()2sin h a a a π∴=---------------------------------------------------------------------------------------------------10分函数()()21ax f x x R x =∈+是奇函数,且,2a ππ⎡⎤∈⎢⎥⎣⎦, 0x ∴>时,()20112ax a af x x x x<==≤++,当1x =时取得最大值2a0x ∴=时,()00f =0x ∴<时,(),02a f x ⎡⎫∈-⎪⎢⎣⎭, ∴函数()f x 的最小值为()2af x =-最小,----------------------------------------------------------------------12分 要使对任意x R ∈,()()f x h a >恒成立,则()()f x h a >最小2sin 2a a a π∴->-, 即不等式2sin 02a a a π-->在,2a ππ⎛⎤∈ ⎥⎝⎦上有解, a π=符合上述不等式,∴存在满足条件的实数a ,使对任意x R ∈,()()f x h a >恒成立,---------------------------------------14分(附:求()2af x =-最小的方法二如下)当0,,2b a ππ⎛⎤=∈ ⎥⎝⎦时,()21ax f x x ∴=+,()()222011ax a f x x x -+'∴==⇒=±+ 当x 变化时,'()f x 与()f x 的变化情况如下表:又0x >时,()0f x > ()2f x ∴=-最小福建省厦门双十中学2014届高三热身考数学(文)试卷(说明:大题的答案必须写在虚线内,否则无效;必须用黑色签字笔书写)一、二、 13 14.15. 16.班级 姓名 班级座号 考场 考场座号17. 18.-----------------------------------------------------------------------------------------------------------------------------------------19、 20、 21、 19.--------------------------------------------------------------------------------------------------------------------------------------------- 22、。