下载文档原格式
过程控制系统课程设计题目之十三大纯滞后过程特性Smith 预估控制对于一个大纯滞后过程特性的对象：s PC e s s s G 10)12)(3(1)(-++=，试设计一个Smith 预估控制系统，并用SIMULINK 和MATLAB 程序仿真实现。
当系统设定值R(s)为1时，调整PI 参数，使过渡过程尽可能满意。
（假设检测变送环节的传递函数为1）；比较在预估模型有偏差时，在相同的输入条件下，与预估模型无偏差情况的仿真结果；如果系统有扰动信号F(s)为单位阶跃信号或SINS 信号时，比较系统的仿真结果；如有可能，再试设计一种改进的Smith 预估器。
实验报告要求： 1、供系统仿真图；2、按照题目要求，给出每个实验的仿真结果图；3、根据以上仿真结果，分析)(s G PC 有滞后与无滞后情况下，PI 参数整定的特点。
大纯滞后过程特性Smith预估控制摘要：Matlab 是一套高性能的数值计算和可视化软件。
它集数值分析、矩阵计算、信号分析与图形显示为一体，构成的一个方便的、界面友好的用户环境。
历经二十几年的发展和竞争，现已成为国际公认的最优秀的科技应用软件。
Matlab 最突出的特点就是简洁、它用直观的、符合人们思维习惯的代码、代替C 语言和FORTRAN 语言的冗长代码。
为此，Matlab 获得了对应用学科的极强适应力。
在国内外高校、Matlab 已成为大学生，硕士生、博士生必须掌握的基本技能。
在设计研究学位和工业部门，Matlab 已经成为研究和解决各种具体工程问题的一种标准软件。
Matlab 软件广泛用于数字信号分析，系统识别，时序分析与建模，神经网络、动态仿真等方面有着广泛的应用。
利用Matlab 这个最优秀的科技软件，把计算机技术与信号分析紧密地结合起来，对信号进行分析处理仿真研究，经实例验证，取得了非常好的效果，具有一定的实用价值。
本文控制系统为研究主体，提出一种Smith 预估控制算法，通过设计自适应非线性反馈回路来自适应调节参数，从而满足对象参数大幅度变化的要求。
基于Matlab参数辨识的纯迟延系统预估控制在火电厂的应用邢红涛【摘要】在探讨Smith预传器的控制原理的基础上,针对制约其工程应用的参数估计问题阐述了一种用Matlab软件计算的工程案例.在分析其应用前景的同时,提出将DCS控制系统、Matlab软件和Smith控制有机结合的思路.【期刊名称】《河北电力技术》【年(卷),期】2008(027)004【总页数】3页(P12-13,27)【关键词】纯迟延;预估控制;Smith预估器;Matlab参数辨识【作者】邢红涛【作者单位】河北省电力研究院,石家庄,050021【正文语种】中文【中图分类】TP2721 概述在工业过程控制中，许多被控对象具有纯迟延的性质，在火电厂自动控制系统中也是如此。
这些系统由于能量或物料在介质中的传输，使被控参数惯性大，不能及时反映扰动量或控制量的变化。
在工业过程控制领域以传统PID控制为主，对于不能及时反馈偏差变化的纯迟延系统,PID控制这种基于偏差的控制方式，控制效果较差。
在应用于某些时滞大的对象时，还可能出现系统闭环稳定性降低、动态过程变差、调节品质恶化的现象。
所以，大惯性的纯迟延过程在传统控制领域是公认的控制难题。
2 Smith预估器的控制原理Smith预估器是一种对大迟延系统进行补偿的控制算法。
该方法的基本原理是：在获取控制对象的基本结构和参数的前提下，由预估器对时滞进行补偿，使被延迟的被调量(偏差)提前反映，从而减小纯迟延造成的影响，提高系统的稳定性和控制品质。
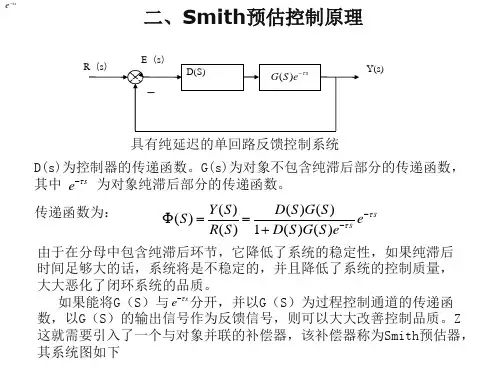
如图1所示的控制系统，其闭环传递函数为：φ(1)图1 带纯迟延控制系统的等效框图其中，R为输入，E1为偏差，D为扰动，X为被控对象输出，Y为输出信号，GC、G0为传递函数。
其特征方程为1+GC(S)G0(S)e-ts=0。
可见特征方程中出现了纯迟延环节，使系统的稳定性降低。
如果t足够大，系统将会失去稳定。
对系统的内部特征进行分析后可知道，信号X在进入纯迟延环节前是没有延迟的，输出信号Y 是X经t延迟后的重复。
实验三S m i t h预估 The following text is amended on 12 November 2020.实验报告||实验名称Smith预估控制算法设计实验课程名称计算机控制技术与系统||实验三 Smith 预估控制算法设计实验1、实验目的在控制算法学习的基础上，根据给定对象特性设计Smith 预估控制器算法，并利用Matlab 软件进行仿真实验，同时与PID 算法控制算法进行比较，加深对该控制算法的掌握和理解。
2、系统结构框图Smith 预估控制系统框图为：3、实验过程及分析设广义被控对象为要求一：取τ=2、T 1=，取采样时间T=1s ，采用零阶保持器，使用Matlab 函数求取出广义对象的z 传递函数；实验过程：使用matlab 求z 传函的函数：clc;clear all;close all;T=1;T1=;tao=2;G0=tf([1],[T1 1],'inputdelay',tao)sysd=c2d(G0,T,'zoh')上述函数将s 传函210(s) 2.881s G e s -=+转化为z 传函20.29340(z)0.7066G z z -=-。
要求二：通过对象阶跃响应曲线，整定PID 参数，采用常规PID 进行给定值扰动和外部扰动响应实验，并绘制控制器输出P 和系统输出y 响应曲线； 实验过程：借助matlab 软件中的simulink 搭建系统仿真模型。
首先将外部扰动置零，利用阶跃响应曲线来整定PID 参数。
利用试凑法整定PID 参数。
PID 控制器的数学描述如下。
首先只给比例作用，调节系统使其稳定；其次加入积分作用消除系统静差；最后加入微分作用。
最后合理调整各个参数，使系统品质达到最优。
经过整定，最终选取P=，I=，D=0，N=100，系统可以相对较好的稳定下来。
输出的曲线如下在30T 的时候在对象之前加入的阶跃干扰，在50T 的时候在对象之后加入幅值为的阶跃扰动，得到的系统的输出曲线如下。
大纯滞后在对象控制方法应用研究摘要：针对一般工业过程中存在的大纯滞后问题，提出了一种克服大纯滞后的预测控制方法。
利用递推最小二乘法进行参数估计，获得对象的一阶简化模型,提出了一种Smith预估神经元控制器设计方法，再用构建的神经网络预测模型预测出未来相应时刻的系统输出，然后用该输出来调整当前时刻的控制量，从而达到预期的控制目的,仿真结果验证了该方法的有效性。
关键词：神经网络；预测控制；大纯滞后0 前言一般工业过程中都具有非线性大纯滞后的特点，特别是滞后较大(即额定滞后S/T>0.5)的系统,常规控制往往无能为力。
采用Smith控制是解决对象大纯滞后问题的有效方法，但它需要建立对象的精确的数学模型，而且鲁棒性和抗干扰能力较差，面向对象的神经元模型及其学习算法具有算法简单、适应性好等优点，但是对于大纯滞后过程，由于被控量的偏差不能及时反映控制量的变化影响了神经元的控制效果。
预测控制是上世纪70年代兴起的一种新控制算法，在工业上已被广泛应用，其主要思想是：在当前时刻，基于过程的动态模型预测未来一定时域内每个采样周期（或按一定间隔）的过程输出，即可以根据当前的输入预测未来多个时刻的输出，从而根据控制要求调整下一时刻的控制量，有利于对纯滞后系统的控制，将预测函数控制应用于大纯滞后温度控制系统，减少了稳态静差，但超调量偏大，要有一种具有自补偿功能的非线性预测反馈校正法，提高了系统的鲁棒性，但该方法限于纯滞后时间已知的情况下，对于纯滞后参数未知或者改变的情况未加讨论。
根据上述情况提出一种用神经网络辨识系统的滞后时间参数，用预测控制算法实现对大纯滞后对象的控制方法。
其中预测模型是用神经网络逼近被控的动态对象而建立的，从而无需知道系统的精确数学模型。
1 神经元模型及控制系统1.1神经元模型针对将神经网络直观套用于自动控制中存在的局限性,提出了一种面向控制的神经元模型它的输出u(t)可以表示为u(t)=K∑wi(t) xi(t) (1)式中：K>0，为神经元的比例系数；xi(t)为神经元的n个输入状态；wi(t)为相应于xi(t)的加权值；wi(t)由某种学习算法确定。
Smith预估器控制设计《计算机控制》课程设计报告题⽬: Smith预估器控制设计姓名: 学号:姓名: 学号:姓名: 学号:2010年12⽉3⽇《计算机控制》课程设计任务书指导教师签字：系（教研室）主任签字：2010年7 ⽉5 ⽇Smith 预估器控制设计⼀．实验⽬的被控对象为ses G s+=-110)(1.0，画出系统框图，设计Smith 数字预估器。
三．控制系统仿真 1.⽅案设计已知纯滞后负反馈控制系统，其中其中D(s)为调节器传递函数，ses G s+=-110)(1.0为对象传递函数，其中G 0(s)e -0.1s包含纯滞后特性,纯滞后时间常数τ=0.1。
系统的特征⽅程为：0.1101()()1()01seD s G s D s s-+=+=+由于闭环特征⽅程中含有0.1se -项，产⽣纯滞后现象，有超调或震荡，使系统的稳定性降低，甚⾄使系统不稳定。
为了改善系统特性，引⼊Smith 预估器，使得闭环系统的特征⽅程中不含有0.1se-项。
Smith 纯滞后补偿的计算机控制系统为:上图所⽰Z O H 为零阶保持器，传递函数：1()Tsh e G s s--=并且有：lT τ=（l 为⼤于1的整数，T 为采样周期）。
2.采样周期T 的选择采样周期在计算机控制中是⼀个重要的参数。
从信号保真度看，采样周期不宜太长，即采样频率不应该过低。
Shannon 采样定理给出了下限⾓频率ωs ≧2ωmax ，ωmax 为原信号的最⾼频率；采样周期应尽可能的短，以使采样后的离散信号可以近似于连续信号，数字控制具有接近于连续控制系统的质量。
但采样频率过⾼，将使得数据存数容量加⼤，计算⼯作量加⼤，并且采样频率⾼到⼀定程度，对系统性能的改善效果并不显著。
所以，我们要找到⼀个最佳的采样周期。
纯滞后较⼤不可忽略时，可选择T 在/10τ附近，当纯滞后占主导地位时，可选择T 约为τ，再加上参考课本上表3.4扩充响应曲线法选择数字PID 参数计算公式，预选了l =2，3，5，10。
石灰窑煅烧石灰石温度优化控制摘要：石灰是生产活性纳米碳酸钙的主要原料，是经石灰窑煅烧石灰石获得。
煅烧是生产活性纳米碳酸钙的首要、重要环节，影响着其质量高低。
而在石灰窑煅烧石灰石中，温度是重要因素，因煅烧是复杂过程，有大纯滞后、非线性及耦合特性，会影响温度稳定性。
且目前使用的上位机检测温度及人工经验加减料控制煅烧温度的生产率较低、质量不稳定，最终不利于石灰活性。
所以，优化控制石灰窑煅烧石灰石的温控非常重要。
本文就分析了石灰窑组成及煅烧工作原理，建立了温度控制数学模型，设计出了模糊免疫自适应 PID 控制器，以实现对温度的良好控制。
见下文。
关键词：石灰窑煅烧石灰石温度控制活性纳米碳酸钙是无机粉填料，其具有纯度高、易得、价廉、无毒特征，被大量用于塑胶、橡胶、建材、化工、油墨等添加剂[1]。
纳米碳酸钙主要是经石灰窑煅烧石灰石而获得，过程中，其温度控制对质量影响较大，良好的温度控制能保证纳米碳酸钙的活性。
所以，对石灰窑煅烧石灰石温度控制非常重要。
但影响温度的因素较多，且检测技术不完善，无法精确重要参数，再加上煅烧过程反应较复杂，一般解析方法无法获取准确的关系模型数据，达不到温度控制系统要求，最终影响质量。
为了确保石灰窑煅烧时的热工及热力分布达到水平，使其能持续稳定的工作，优化温度恒定控制是关键。
我国已有众多学者对石灰窑温度控制问题进行了研究，均采用了模糊PID控制，但随着对活性要求、生产效率、节能减排的严格要求，常规PID难以达到控制要求[2]。
因此，寻求更适合的温度控制模型非常必要。
1石灰窑的组成及煅烧石灰石工作原理1.1组成常见石灰窑为机械式立窑，由上料机构、主体、卸料设备、风机等组成，其中，主体由受料斗、布料器、出料机组成。
窑体上半部分是圆直筒型，下半部分是圆锥形，窑衬由耐火黏土砖筑成，钢窑壳约8-12mm后。
将石灰窑分为预热区、煅烧区、冷却区、窑尾窑气出口、窑头生石灰出口，并安有11个热电偶以检测温度。
