大迟延和复杂控制系统

课程设计报告学院电子信息学院专业控制理论与控制工程学生显班级学号132030032指导教师杜昭平二零一四年四月串级控制系统原理及应用一串级控制系统的根本概念1 串级控制系统近二十年，控制技术获得了惊人的成就，已在工业生产和科学开展中起着关键作用。

而且，控制系统已成为大量设备不可分割的重要组成局部。

控制自动化的程度已成为衡量工业企业现代化的一个重要标志。

在众多复杂的控制系统中，串级控制系统在电机控制中的应用更为普遍，串级控制系统是一个双回路系统，一个控制器的输出控制另一个控制器的设定值，这种构造称为串级控制系统。

串级控制系统实质上是把两个调节器串接起来，通过它们的协调工作，使一个被调量准确保持为设定值]1[。

通常，串级系统副环的对象惯性小，工作频率高，而主环惯性大，工作频率低。

2 串级控制系统的组成串级控制系统整个系统包括两个控制回路，主回路和副回路。

副回路由副变量检测变送、副调节器、调节阀和副过程构成；主回路由主变量检测变送、主调节器、副调节器、调节阀、副过程和主过程构成。

主要由以下元件构成：〔1〕主调节器和副调节器两个调节器〔2〕两个测量变送器〔3〕一个执行器〔4〕一个调节阀们〔5〕被控对象组成系统原理框图如图1－1所示。

图1－1 串级控制系统原理方框图〔1〕系统中的两个调节器相互串联，前一个调节器的输出作为后一个调节器的输入。

这两个调节器分别叫作主调节器和副调节器，即主调节器的输出进入副调节器，作为副调节器的给定值。

〔2〕串级控制系统中有两个反应回路，并且一个回路嵌套在另一个回路之中，处于里面的回路称为回路〔副回路〕，处于外面的回路称为外回路〔主回路〕。

〔3〕串级控制系统中有两个测量反应信号，称为主参数和副参数，分别作为主、副调节器的反应输入信号。

二串级控制系统实例——火电厂主汽温度串级控制系统2.1 应用现状火电厂中，为更好的对主蒸汽温度进展控制，通常将过热器分为两段，即高温段和低温段，在之间装有一个喷水减温器，喷水减温器是一个三通容器，分别与低温段过热器、高温段过热器以及冷水〔减温水〕管道连通，蒸汽从低温段流经喷水减温器，再进入高温段。

一种大迟延系统的控制方法马平;李奕杰【摘要】大迟延系统在工业生产过程中比较常见但又难以控制,并且大部分工业生产过程都具有非线性的特征,被控对象的传递函数随负荷的变化而变化.在利用传统串级PID对实际系统进行控制的时候,很难得到理想的控制效果,难以保证控制品质,因此针对此问题提出基于物理机理的PID控制方法.该方法的控制策略主要是基于被控对象和控制过程的物理机理,使其可以不需要经过复杂的计算和补偿环节,取消了串级控制回路,从而使系统结构更加简单有效,控制性能得到较大改善,可适应大范围负荷变化的需要.由于火电厂主汽温为典型的大惯性、大迟延、非线性系统,被控对象的传递函数随负荷的变化而改变,所以选取主汽温为被控对象进行仿真实验.实验结果证明,基于物理机理的PID控制与传统串级PID相比,可以达到更好的控制效果.%In the industrial production process,the large delay system is comparatively common and get difficult to be controlled one. Most of them are nonlinear and their transfer function varies with load. U-sing traditional serial PID for control of practical system, it is difficult to get an ideal control effect and hard to ensure the control quality. In view of above-mentioned facts, a physical mechanism-based PID control method was presented. Its control strategies were mainly based the physical mechanism of the controlled objects and control process without complex calculation and compensation link, where the cascade control loop was canceled, so that the system structure became simpler and more effective, and its control performance got very great improvement, meeting the requirement of wide range of load variation. In power plant, the mainsteam temperature is a typical large-inert, long delayed, and nonlinear system. The transfer function of the controlled object varies with the load. Therefore, the main steam temperature was taken as the controlled object to carry out the simulation experiment. The experimental result showed that, compared with the traditional cascade PID control, the PID control based on physical mechanism would be able to achieve better control effect.【期刊名称】《兰州理工大学学报》【年(卷),期】2012(038)006【总页数】4页(P66-69)【关键词】基于物理机理的PID控制;过热汽温;扰动;大迟延【作者】马平;李奕杰【作者单位】华北电力大学自动化系,河北保定071000;华北电力大学自动化系,河北保定071000【正文语种】中文【中图分类】TP273大迟延系统在工业生产过程中比较常见但又是难以控制的，一直是控制界关注的研究方向［1］.利用传统串级PID对实际系统进行控制的时候，得到理想的控制效果相当困难，难以保证控制品质［2］.而基于物理机理的PID控制可以很好地解决此问题.并且通过仿真实验与传统的串级PID控制效果比较，更能突显出基于物理机理的PID控制的优势.1 基于物理机理的PID控制1.1 传统串级PID控制的缺陷现在工程上针对大惯性大迟延系统往往采用串级PID控制.串级系统和简单系统有一个显著的区别，即其在结构上形成了两个闭环.一个闭环在里面，被称为副环或者副回路，在控制过程中起着“粗调”的作用；一个环在外面，被称为主环或主回路，用来完成“细调”任务，以最终保证被调量满足工艺要求［3］.系统内回路整定后可约等于1，此时系统的震荡频率取决于系统的惰性区G01（s），而G01（s）仍然为具有较大迟延的对象，因此这种控制结构在负荷扰动下，系统超调量大、调节时间长的特性不能得到有效的改善.1.2 基于物理机理的PID控制原理对于大惯性大迟延系统基于物理机理的PID控制的控制策略主要基于被控对象和过程的物理机理，可以不需要复杂的计算和补偿环节，取消了串级控制回路，系统结构更加简单、有效，可适应大范围负荷变化的需要［4］.基于物理机理的PID控制的系统原理如图1所示，其中K为调整因子，G01（s）为系统的惰性区，G02（s）为导前区.图1 基于物理机理的PID控制系统结构Fig.1 Configuration of physical mechanism-based PID control system系统构建了基于对象机理模型的局部反馈G′01（s），反馈与对象相关联，系统在本质上变成开环，消除了系统的震荡和超调.系统的开环传递函数如下：得出系统的特征方程为代入式（1）以及系统的特征方程，得出：当时，系统的特征方程转化为则式（1）可简化为化简后系统的原理图如图2所示.可以看出，系统的震荡频率取决于G02（s），而对于大惯性大迟延的系统，往往G02（s）的震荡频率比G01（s）小很多，调节对象成为快速响应对象而不再是大惯性对象，参数整定十分容易，系统的震荡频率减小，调节器的输出更加平和，调节器出现震荡的可能性大大减小，负荷扰动下，系统超调量大，调节时间长的特性得到了有效改善.图2 基于物理机理的PID控制系统化简后方框原理图Fig.2 Simplified block diagram of physical mechanismbased PID control system系统的误差传递函数为得出系统的稳态误差为将式（1，3，4）代入式（7）可得当s→0时，GPID（s）→∞，1+GPID（s）G02（s）可以等效为GPID（s）G02（s），所以稳态误差为g（s）是动态环节，可表示为，当s→0时，g（s）等于1，所以得出系统的稳态误差等于0.2 基于物理机理的火电厂过热汽温控制设计2.1 过热汽温对象特性分析由火电厂主汽温在不同负荷下的被控对象传递函数［5］（见表1）即可以得出其为大惯性、大迟延、非线性的系统，被控对象的传递函数随负荷的变化而改变.目前电厂过热器调节方法主要采用喷水减温方法，过热蒸汽温度控制系统采用串级控制或导前汽温微分信号的双回路控制［6］.当工况变化大时，难以保证控制品质，因而考虑采用基于物理机理的PID汽温调节.表1 不同负荷下的被控对象传递函数Tab.1 Transfer function of controlled object with different loads负荷/%导前区惰性区100 G02（s）=1.58（14s+1）2 G01（s）= 2.45（15.8s+1）4 88 G02（s）=2.01（16s+1）2G01（s）= 2.09（22.3s+1）4 62 G02（s）=4.35（19s+1）2 G01（s）= 1.83（28.2s+1）4 44 G02（s）=6.62（21s+1）2 G01（s）= 1.66（39.5s+1）42.2 基于物理机理过热汽温结构设计根据过热汽温的实际情况，得出基于物理机理的PID控制的过热汽温控制原理图如图3所示，图3依然可以简化为图2的形式.其中，输入为过热器出口汽温设定值Tsp，输出为过热器出口汽温Tout，实际工程中通过f（x）来实现K的取值，，K为G01（s）在不同负荷下的增益的倒数.图3 过热汽温的基于物理机理的PID控制系统结构Fig.3 Configuration of physical mechanism-based PID control system for superheated steam temperature control当G′01（s）与实际 G01（s）的特性充分接近时则整个动态调整过程基本维持恒定，整个汽温调节系统转换为以过热器进口汽温为对象的单回路系统［7］.模拟的过热器特性的G′01（s）随着负荷的改变会发生变化，即可以通过负荷与多容环节时间常数的关系曲线实现不同负荷下的过热器的特性.同时调整因子也随负荷的变动而发生改变.过热器特性的G′01（s）和调整因子并不总是很准确的，但 Tout总能稳定到设定点［8］.本文分别针对负荷为100%、88%、62%、44%的情况对被控对象进行研究.被控对象传递函数见表1.2.3 仿真研究为了检验证明本文提出的控制策略的有效性和优越性，根据在不同负荷系统出现的不同扰动，做了两组扰动仿真实验，并和传统串级PID加入同样的扰动进行比较. 过热汽温基于物理机理的PID控制的系统原理如图3所示，因为G′01（s）模拟的是过热器的特性，G′01（s）的模型为在不同负荷下分别加入给定值扰动和调节量扰动，系统的响应曲线如图4和图5所示，虚线为常规串级PID控制，实线为基于物理机理的PID控制.图4 四种不同负荷下给定值扰动的响应曲线Fig.4 Curves of response of system with four different loads to definite-valued disturbance图5 四种不同负荷下调节量扰动下的响应曲线Fig.5 Curves of response of system with four different loads to disturbance of adjusting magnitude从仿真结果可以看出，相对于常规的PID控制策略，采用基于物理机理的PID控制策略在出现调节量扰动时有更小的超调，并且调节时间要短.本文在对负荷扰动进行研究时，将100%、88%负荷作为第一组，62%、44%负荷作为第二组，即把100%负荷下的G01（s）换成88%负荷下的G01（s），88%负荷下的G01（s）换成100%负荷下的G01（s），观察控制效果的变化，第二组做同样的研究，并与串级相同的扰动仿真，然后进行比较.系统的响应曲线如图6所示，虚线为常规PID控制，实线为基于物理机理的PID控制.图6 四种负荷扰动下不同负荷扰动下的响应曲线ig.6 Curves of system response to disturbance of four loads从仿真结果可以看出，相对于常规的PID控制策略，采用基于物理机理的PID控制策略在出现负荷扰动时有更小的超调，并且调节时间要短.3 结论本文针对大惯性、大迟延、非线性系统提出了一种基于被控对象和过程物理机理的PID控制策略，使其可以不需要复杂的计算和补偿环节，取消了串级控制回路，从而使系统结构更加简单和有效，可适应大范围负荷变化的需要.通过以火电厂主汽温为被控对象的仿真，验证了基于物理机理的PID控制策略的有效性和较传统串级PID控制的优越性.基于物理机理的PID控制策略不仅具有更小的超调量、更强的抗干扰能力和更好的自适应性，并且算法原理简单，使其可以方便地应用于工业控制中，具有很好的工业应用前景.参考文献：［1］李长更，刘友宽，苏杰.模型算法控制对大迟延系统的控制效果研究［J］.仪器仪表用户，2010，17（4）：5-7.［2］王丽珍.模糊PID控制器在过热汽温控制中的应用［J］.机械工程与自动化，2009（1）：129-131.［3］金以慧，方崇智.过程控制［M］.北京：清华大学出版社，2009：112-114. ［4］夏明.超临界机组汽温控制系统设计［J］.中国电力，2006，39（3）：74-77.［5］李建强，杨铎烔.基于灰色预估PID控制的过热汽温控制［J］.华北电力大学学报：自然科学版，2011，38（1）：71-74.［6］车得福，庄正宁，李军，等.锅炉［M］.西安：西安交通大学出版社，2004：276-282.［7］张华，孙奎明，张磊.热工自动化［M］.北京：中国电力出版社，2010：76-78.［8］李致远.基于单神经元自适应PID的过热汽温控制系统研究［J］.工业控制计算机，2011，23（8）：65-66.。

施密斯预估控制姓名：学号：班级：1 实验目的对大多数控制系统，采用常规的控制技术均可以达到满意的控制效果，但对于复杂及特殊要求的控制系统，采用常规的控制室技术很难达到目的，在这种情况下，就需要采用复杂控制技术，其中Smith 预估控制算法是常用的一种，通过本实验加深对Smith 预估控制算法的理解和掌握。

2 实验原理图1为被控对象具有纯滞后特性的单回路反馈控制系统，D （s ）是控制器，被控对象的传递函数为etss -)(G p ，其中，)(G p s 为被控对象中不包含纯滞后部分的传递函数，ts-e为被控对象纯滞后部分的传递函数。

)(t r )(t e )(t u )(t y_施密斯预估原理：与D （s ）并接一补偿环节，用来补偿被控对象中的纯滞后部分，这个补偿环节称为预估器，其传递函数为)1)((G p tse s --，t 为纯滞后时间，补偿后的系统结构如图2所示。

)(t r )(t e )(t u )(t y_ _)(t y τ由施密斯预估控制器)1)((G p tses --和控制器D （s ）组成的回路陈伟纯滞后补偿器，)(s Ds e s τ-)(G p)(s Ds e s τ-)(G p)1)((G p ts e s --其传递函数为：)1)(()(1)()(D m s p e s G s D s D s τ--+=经过补偿后的系统闭环传递函数为：s p p sp m sp m e s G s D s G s D es G s D e s G s D τττ---+=+=Φ)()(1)()()()(1)()(s ）（该式说明，进过补偿后，消除了之后部分对控制系统的影响，因为式中ts-e 在闭环控制回路之外，不影响系统的稳定性。

设广义被控对象为：1011()()()1Ts s se e H s G s G s es T sττ----==⋅+取T=1、τ=2、T 1=2.88，经采样（T=1s ）保持后，其广义对象z 传递函数为00.2934()0.7066G z z =-，而2se -转换为2个单位迟延。

摘要目前，由于PID结构简单，可通过调节比例积分和微分取得基本满意的控制性能，广泛应用在电厂的各种控制过程中。

电厂主汽温被控对象是一个大惯性、大迟延、非线性且对象变化的系统，常规汽温控制系统为串级PID控制或导前微分控制,当机组稳定运行时,一般能将主汽温控制在允许的围。

但当运行工况发生较大变化时,却很难保证控制品质。

因此本文研究基于BP神经网络的PID控制，利用神经网络的自学习、非线性和不依赖模型等特性实现PID参数的在线自整定，充分利用PID和神经网络的优点。

本处用一个多层前向神经网络，采用反向传播算法，依据控制要时输出Kp、Ki、Kd，依次作为PID控制器的实时参数，代替传统PID参数靠经验的人工整定和工程整定，以达到对大迟延主气温系统的良好控制。

对这样一个系统在MATLAB平台上进行仿真研究，仿真结果表明基于BP神经网络的自整定PID控制具有良好的自适应能力和自学习能力，对大迟延和变对象的系统可取得良好的控制效果。

关键词：主汽温，PID，BP神经网络，MATLAB仿真ABSTRACTAt present, because PID has a simple structure and can be adjusted proportional 、integral and differential to satisfactory control performance, it is widely used in power plants of various control process. The system of power plant main steam temperature is an large inertia、big time-delayed and nonlinear dynamic system. Conventional steam temperature control system adopted cascade PID control or the differential control of lead before. When the unit is stable, these methods will control the steam temperature in a certain range ,but when operating conditions changed greatly, it is difficult to ensure the quality of control. This article studies PID control based BP neural network . Using such characteristics of neural network self-learning, nonlinear and don't rely on model realize PID parameters auto-tuning. It can make full use of the advantages of PID and neural network. Here, we use a multilayer feedforward neural network using back propagation algorithm. This net can real-time output Kp, Ki, Kd as the PID controller parameters , insteading of the traditional PID parameters determined by experience, so it can obtain good control performance .For such a system ,we can simulate in MATLAB simulation platform. The simulation results show that the PID control based BP neural network has good adaptive ability and self-learning ability. For the system of large delay and free-model can obtain good control effect.KEY WORDS: main steam temperature ，PID ，BP neural network， MATLAB simulation目录摘要 (I)ABSTRACT (II)第一章绪论 (1)1.1 选题背景和意义 (1)1.2 国外研究现状 (1)1.3 立论依据 (5)1.4 本文所做的主要工作 (6)第二章神经网络的基本原理 (8)2.1 人工神经元模型 (8)2.2 神经网络的学习方式和学习规则 (9)2.2.1 神经网络的学习方式 (9)2.2.2 神经网络的学习规则 (9)2.3 神经网络的特点及应用 (10)2.4 BP神经网络 (11)2.4.1 BP神经网络的结构 (11)2.4.2 BP神经网络的算法 (12)2.5 本章小结 (16)第三章基于BP神经网络的PID控制 (17)3.1 PID控制器的离散差分方程 (17)3.2 基于BP神经网络的PID整定原理 (18)3.3 基于BP神经网络的PID控制算法流程 (22)3.4 本章小结 (22)第四章基于BP神经网络的PID控制在主汽温控制系统中的应用 (23)4.1 主汽温的控制任务 (23)4.2 主汽温被控对象的动态特性 (23)4.3 主汽温控制策略 (24)4.3.1 主汽温控制信号的选择 (24)4.3.2 主汽温控制的两种策略 (26)4.4仿真分析 (27)4.5 本章总结 (34)结论与展望 (35)参考文献 (37)致 (39)第一章绪论1.1 选题背景和意义在控制系统设计中,最主要而又最困难的问题是如何针对复杂、变化及具有不确定性的受控对象和环境作出有效的控制决策。

一、常规PID控制规律常规PID控制即比例-积分-微分控制规律。

比例调节作用是最基本的调节作用，使长劲”比例作用贯彻于整个调节过程之中；积分和微分作用为辅助调节作用。

积分作用则体现在调节过节过程的后期，用以消除静态偏差，使后劲”微分作用则体现在调节过程的初期，使前劲”。

4. PID（比例-积分-微分）控制特点（1）缺点不适用于有大时间滞后的控制对象，参数变化较大甚至结构也变化的控制对象，以及系统复杂、环境复杂、控制性能要求高的场合。

（2）优点:• PID算法蕴涵了动态控制过程中过去、现在和将来的主要信息，而且其配置几乎最优。

比例（P）代表了当前的信息，起纠正偏差的作用，使过程反应迅速。

微分（D）在信号变化时有超前控制作用，代表了将来的信息。

在过程开始时强迫过程进行，过程结束时减小超调，克服振荡，提高系统的稳定性，加快系统的过渡过程。

积分⑴代表了过去积累的信息，它能消除静差，改善系统静态特性。

此三作用配合得当，可使动态过程快速、平稳、准确，收到良好的效果。

•PID控制适应性好，有较强鲁棒性。

• PID算法简单明了，形成了完整的设计和参数调整方法，很容易为工程技术人员所掌握。

•许多工业控制回路比较简单，控制的快速性和精度要求不是很高，特别是对于那些I〜2阶的系统，PID控制已能得到满意的结果。

•PID控制根据不同的要求，针对自身的缺陷进行了不少改进，形成了一系列改进的PID 算法。

2.调节器的参数整定就是合理地设置调节器的各个参数，在热工生产过程中，通常要求控制系统具有一定的稳定裕量，即要求过程有一定的衰减率® ;在这一前提下，要求调节过程有一定的快速性和准确性，换言之稳定性是首要的。

所谓准确性就是要求控制过程的动态偏差（以超调量MP表示）和静态偏差（esS尽量地小，而快速性则是要求控制过程的时间尽可能地短。

控制系统参数整定有理论计算方法、工程整定方法。

热工系统的主要控制方式一•反馈控制反馈控制是根据被调量与给定值的偏差值来控制的。

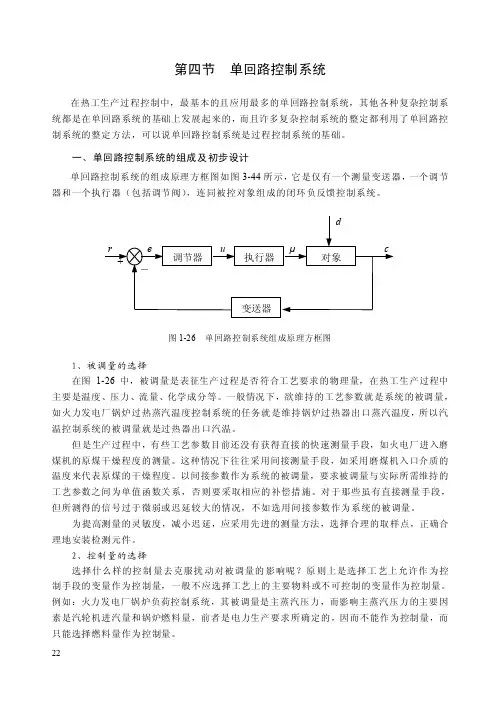
第四节单回路控制系统在热工生产过程控制中，最基本的且应用最多的单回路控制系统，其他各种复杂控制系统都是在单回路系统的基础上发展起来的，而且许多复杂控制系统的整定都利用了单回路控制系统的整定方法，可以说单回路控制系统是过程控制系统的基础。

一、单回路控制系统的组成及初步设计单回路控制系统的组成原理方框图如图3-44所示，它是仅有一个测量变送器，一个调节器和一个执行器（包括调节阀），连同被控对象组成的闭环负反馈控制系统。

图1-26 单回路控制系统组成原理方框图1、被调量的选择在图1-26中，被调量是表征生产过程是否符合工艺要求的物理量，在热工生产过程中主要是温度、压力、流量、化学成分等。

一般情况下，欲维持的工艺参数就是系统的被调量，如火力发电厂锅炉过热蒸汽温度控制系统的任务就是维持锅炉过热器出口蒸汽温度，所以汽温控制系统的被调量就是过热器出口汽温。

但是生产过程中，有些工艺参数目前还没有获得直接的快速测量手段，如火电厂进入磨煤机的原煤干燥程度的测量。

这种情况下往往采用间接测量手段，如采用磨煤机入口介质的温度来代表原煤的干燥程度。

以间接参数作为系统的被调量，要求被调量与实际所需维持的工艺参数之间为单值函数关系，否则要采取相应的补偿措施。

对于那些虽有直接测量手段，但所测得的信号过于微弱或迟延较大的情况，不如选用间接参数作为系统的被调量。

为提高测量的灵敏度，减小迟延，应采用先进的测量方法，选择合理的取样点，正确合理地安装检测元件。

2、控制量的选择选择什么样的控制量去克服扰动对被调量的影响呢？原则上是选择工艺上允许作为控制手段的变量作为控制量，一般不应选择工艺上的主要物料或不可控制的变量作为控制量。

例如：火力发电厂锅炉负荷控制系统，其被调量是主蒸汽压力，而影响主蒸汽压力的主要因素是汽轮机进汽量和锅炉燃料量，前者是电力生产要求所确定的，因而不能作为控制量，而只能选择燃料量作为控制量。

给定值 调节器 对象被调量 － μ 扰动 扰动 图1-28 单回路调节系统 3、控制通道和扰动通道单回路控制系统的组成如图1-27所示，图中W 01(s )为对象的传递函数，它是包括了检测元件、测量变送器、执行机构和调节阀在内的广义对象特性；W c (s )为调节器的传递函数，D 为扰动信号，W 02(s )为被调量与扰动信号间的传递函数。

过程控制之液位流量串级控制系统1.1控制系统在实际应用中的重要意义单回路控制系统是过程控制中结构最简单的一种形式，它只用一个调节器，调节器也只有一个输入信号，从系统方框图看，只有一个闭环。

在大多数情况下，这种简单系统已经能够满足工艺生产的要求。

但在复杂的控制系统中，则需在单回路的基础上，采取其它措施，组成复杂控制系统，而串级控制系统就是其中一种改善和提高控制品质的极为有效的控制系统。

液位和流量是工业生产过程中最常用的两个参数，对液位和流量进行控制的装置在工业生产中应用的十分普遍。

液位的时间常数T一般很大，因此有很大的容积迟延，如果用单回路控制系统来控制，可能无法达到较好的控制质量。

而串级控制系统则可以起到十分明显的提高控制质量的效果，因此往往采用串级控制系统对液位进行控制。

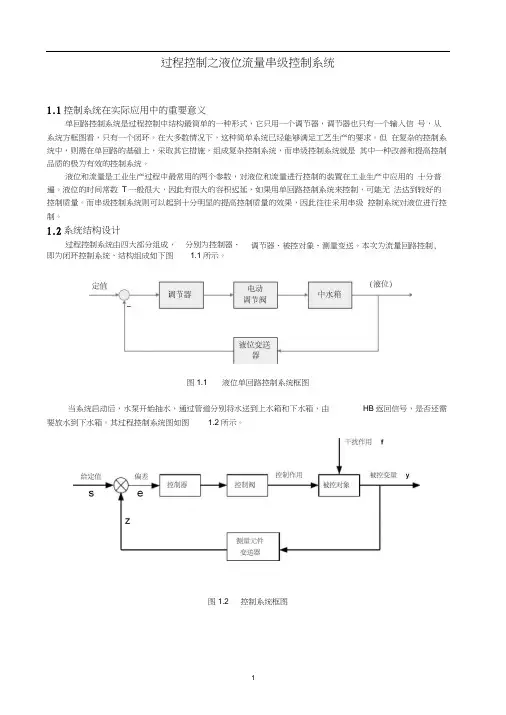
1.2系统结构设计即为闭环控制系统，结构组成如下图 1.1所示。

图1.1 液位单回路控制系统框图当系统启动后，水泵开始抽水，通过管道分别将水送到上水箱和下水箱，由HB返回信号，是否还需要放水到下水箱。

其过程控制系统图如图 1.2所示。

图1.2 控制系统框图过程控制系统由四大部分组成，分别为控制器、调节器、被控对象、测量变送。

本次为流量回路控制,单容水箱如图1.2所示，Qi为入口流量，由调节阀开度μ加以控制，出口流量则由电磁阀控制产生干扰。

被调量为水箱中的水位H,它反映水的流入与流出量之间的平衡关系。

现在分析水位在电磁阀开度扰动下的动态特性。

显然，在任何时刻水位的变化均满足下述物料平衡方程：dH 1Qi - Q Odt F（1.1）其中Qi =k"（1.2）Q。

= k、H（1.3）F为水箱的横截面积；k.!.是决定于阀门特性的系数，可以假定它是常数；k是与电磁阀开度有关的系数，在固定不变的开度下,液位对象的传递函数：2.1控制规律的比较与选择2.1.1常见控制规律的类型及优缺点比较PID控制的各种常见的控制规律如下：一、比例调节（P调节）在P调节中，调节器的输出信号U t与偏差信号e t成比例，即U t 二K C e t (2.1)1.3控制系统的总体方框图及工作过程k可视为常数增量，UO 的大小可以通过调整调节器的工作点加以改变。

上海电力学院课程设计报告课名：控制原理应用实践题目：大延迟过程的PID参数整定院系：自动化工程学院专业：自动化班级：姓名：学号：时间：2014年1月09日一、设计内容及要求1、设计内容已知PID 控制系统受控对象的传递函数为()e sTs K s G τ-+=1，当2/>T τ时，求PID 控制器的参数，要求系统到达稳定时间快，稳态误差ssre 小，最大超调量σp小。

2、设计要求1）绘制Simulink 系统仿真模型；2）根据Z-N 法中2.0/≤T τ，2/2.0≤<T τ时PID 参数的公式推出2/>T τ是PID 的大致规律；3）使用经验法代入仿真模型中确定PID 参数范围；4）根据代入不同数值得出的衰减震荡的阶跃响应曲线进一步确定PID 参数范围；5）大致推导出2/>T τ时PID 各参数的公式；6）利用仿真软件辅助分析设计，并验算公式的使用范围；7）根据Matlab 得出的实验结果，微调2/>T τ时PID 各参数公式，进一步完善上述公式；8）设计完成后提交设计报告；二、参考资料[1]《自动控制原理》教材； [2]《自动控制原理实验指导书》； [3] Matlab 相关书籍；一、 延迟过程的相关设计当传递函数()e sTs K s G τ-+=1，当τ的值很大时，系统趋于稳定的时间将会增加，导致整个系统比较难控，因此需要使用PID 参数整定调节大延迟系统，使系统更加稳定，加大其可控性。

1、设计延迟过程的模拟图形设计一个大延迟过程的传递函数()e sTs K s G τ-+=1,取K=1,T=1, τ=10,得如下传递函数()e ss s G 1011-+=，模拟图形如下图1所示：图12、 绘制延迟系统的响应曲线由上图所示的模拟图形绘制出如下图2的衰减震荡的阶跃响应曲线。

图2二、 Matlab 仿真软件辅助分析设计过程的整定计算公式（后面附有推导理由）：KT T K p )5.0/()1/(*12.0+-=ττ,τ1.04.0+=T Ti, τ1.0=T d 。