卷积码举例
- 格式:ppt
- 大小:105.50 KB
- 文档页数:4



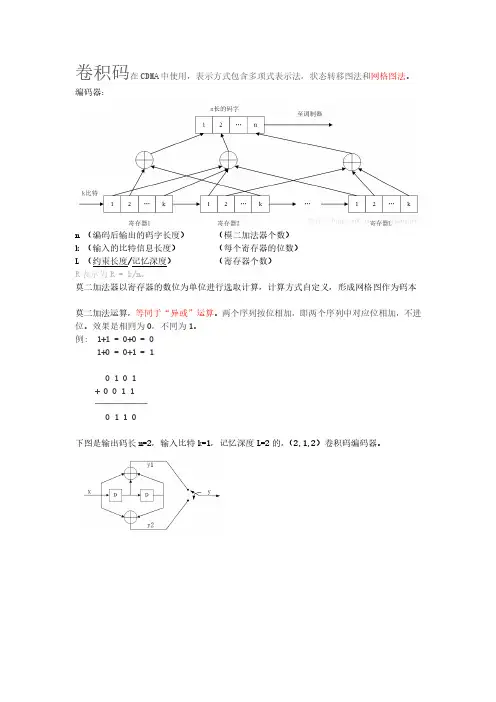
卷积码在CDMA中使用,表示方式包含多项式表示法,状态转移图法和网格图法。
编码器:n (编码后输出的码字长度)(模二加法器个数)k (输入的比特信息长度)(每个寄存器的位数)L (约束长度/记忆深度)(寄存器个数)R表示为R = k/n。
莫二加法器以寄存器的数位为单位进行选取计算,计算方式自定义,形成网格图作为码本莫二加法运算,等同于“异或”运算。
两个序列按位相加,即两个序列中对应位相加,不进位。
效果是相同为0,不同为1。
例: 1+1 = 0+0 = 01+0 = 0+1 = 10 1 0 1+ 0 0 1 1──────0 1 1 0下图是输出码长n=2,输入比特k=1,记忆深度L=2的,(2,1,2)卷积码编码器。
如编码序列“0 1 1 0 0”在图中的序列如下:汉明距离两个二进制数之间进行逐位对比,得到不同的个数如1000,与1100为1,与1110为2,与1111为3维特比算法综合状态之间的转移概率和前一层各状态的概率情况计算出概率最大的状态转换路径,从而推断出隐含状态的序列的情况。
的分支度量(汉明距离)。
其中有两条路径的分支量度为0。
3.寻找最大似然路径 - 译码过程维特比算法的关键点在于,接收机可以使用分支度量和先前计算的路径度量递推地计算当前状态的路径度量。
初始时,状态00代价为0,其它状态代价为正无穷(∞)。
算法的主循环由两个主要步骤组成:首先计算下一时刻监督比特序列的分支度量,然后计算该时刻各状态的路径度量。
路径度量的计算可以认为是一个“加-比-选”的过程1)将分支度量与上一时刻状态的路径度量相加。
2)每一状态比较来自前一时刻状态可达到的所有路径(只有两条这样的路径进行比较)3)每一状态删除其余到达路径,选择最小度量的路径保留(称为幸存路径/存活路径)若进入某个状态的部分路径中,有两条路径的度量值相等,则可以任选其一作为幸存路径。
下图显示了维特比译码的过程。
此例接收到的位序列为11 10 11 00 01 10(偷偷告诉你:这是有误码的信息)此时,产生了具有相同路径度量的四个不同路径,通向这四个状态的任一路径都是可能发送的比特序列(它们都具有度量为2的汉明距离)。


MATLAB第六次预习报告研五队李振坤S201301104线性分组码1. 基本概念●系统码:编码后,信息码元本身不变,只在信息码元后加入监督码元。
●线性码:监督码元和信息码元成线性关系的码型。
●分组码:将信息码分组,并为每组信息码附加若干监督码的编码。
分组码一般用表示,为实际传送的码长,是信息码长,是监督码长。
●线性分组码:分组码的信息码元和监督码元,由一些线性代数方程联系起来。
分组是指编、译码过程是按分组进行的,而线性是指分组码中的监督码元按线性方程生成的。
【注】线性分组码的编码问题,就是要建立一组线性方程组,已知k个系数(即信息码),要求n-k个未知数(即监督码)。
2. 线性分组码的主要性质(1)封闭性封闭性是指码中任意两许用码组之和(逐位模2和)仍为一许用码组,这就是说,若A1和A2为码中的两个许用码组,则A1+A2仍为其中的一个许用码组。
(2)码的最小距离等于非零码的最小重量因为线性分组码具有封闭性,因而两个码组之间的距离(模2减)必是另一码组的重量。
为此,码的最小距离也就是码的最小重量,当然,除全“0”码组外。
3. 汉明码汉明码是用于纠正单个错误的线性分组码,其特点为:(1)最小码距(2)纠错能力【注】(3)监督码长(4)总码长()(5)信息码长()(6)编码效率(当r很大时,R趋向于1,效率高)因此,当r=3,4,5,6……时,分别有(7,4)、(15,11),(31,26),(63,57)等汉明码。
4. (7,4)汉明码在(7,4)汉明码中,码组为,其中为4个信息元,为3个监督码元。
监督码元与信息元之间的关系为:(9-4)生成矩阵G:编码时使用,用于产生整个码组,包括信息码和监督码。
改写为其中称为生成矩阵,它的各行是线性无关的。
为阶单位矩阵;为阶矩阵。
由生成矩阵可以产生整个码组,码组C是系统码(即信息码保持不变,监督码附加其后)。
【注】(1)上述生成矩阵为典型形式,保证能产生系统码。

No.15 (2,1,3)卷积码的编码及译码摘要:本报告对于(2,1,3)卷积码原理部分的论述主要参照啜刚教材和课件,编程仿真部分绝对原创,所有的程序都是在Codeblocks 8.02环境下用C语言编写的,编译运行都正常。
完成了卷积码的编码程序,译码程序,因为对于短于3组的卷积码,即2 bit或4 bit纠错是没有意义的,所以对正确的短序列直接译码,对长序列纠错后译码,都能得到正确的译码结果。
含仿真结果和程序源代码。
如果您不使用Codeblocks运行程序,则可能不支持中文输出显示,但是所有的数码输出都是正确的。
一、 卷积码编码原理卷积码编码器对输入的数据流每次1bit 或k bit 进行编码,输出n bit 编码符号。
但是输出的分支码字的每个码元不仅于此时可输入的k 个嘻嘻有关,业余前m 个连续式可输入的信息有关,因此编码器应包含m 级寄存器以记录这些信息。
通常卷积码表示为 (n,k,m). 编码率 k r n=当k=1时,卷积码编码器的结构包括一个由m 个串接的寄存器构成的移位寄存器(成为m 级移位寄存器、n 个连接到指定寄存器的模二加法器以及把模二加法器的输出转化为穿行的转换开关。
本报告所讲的(2,1,3)卷积码是最简单的卷积码。
就是2n =,1k =,3m =的卷积码。
每次输入1 bit 输入信息,经过3级移位寄存器,2个连接到指定寄存器的模二加法器,并把加法器输出转化为串行输出。
编码器如题所示。
二、卷积码编码器程序仿真 C 语言编写的仿真程序。
为了简单起见,这里仅仅提供数组长度30 bit 的仿真程序,当然如果需要可以修改数组大小。
为了更精练的实现算法,程序输入模块没有提供非法字符处理过程,如果需要也可以增加相应的功能。
进入程序后,先提示输入数据的长度,请用户输入int (整型数)程序默认用户输入的数据小于30,然后提示输入01数码,读入数码存储与input 数组中,然后运算输出卷积码。


关于卷积码编码结果的位数一、问题描述卷积码的编码是我们经常遇到的,在讲解卷积码的输出时,我们都是如下所示的这个典型的(2,1,3)卷积码为例的,其中1111g =,2101g =。
在这个例子的条件下,我们总是可以迅速地求得正确的编码结果,无论使用离散卷积,还是多项式,还是生成矩阵。
但是,实际中可不都是这样的,生成多项式可能出现左侧或者右侧为零的情况,比如1100g =,2001g =之类的,这样就出现了离散卷积或者多项式相乘后位数不正常的情况,使得输出结果存在前后补零的问题。
另外,输入也不见得都是10111u =这样的,也可能出现1011100u =,此时结果又会出现位数上的疑问。
下面就从根源开始,详细说说这个位数的问题。
二、生成多项式含零考虑生成多项式含零的问题,就用最极端的例子,1100g =,2001g =,前者是右侧含零,后者是左侧含零。
为了更有针对性,暂不考虑输入两侧含零的情况,假设输入10111u =。
1、完整输出的位数首先我们需要对正常完整输出的位数有个理解,在输入为5位,1g 长度为3的情况下,上支路输出位数应该是7位,具体计算是5+3-1。
实际上,对于输入n 位,1g 长度为m 的情况,上支路输出位数应该是n +m -1位,其中m -1是寄存器的个数。
也即输入为n 位时,输出完n 位之后寄存器中还存在输入的数据,只有当寄存器的内容跟输入都无关了,才算输出结束,所以输出除了输入的n 位,还会输出跟寄存器数量相等的m -1位。
当然,这里只讨论了一个支路,总的输出位数应该是n +m -1乘以输出路数。
所以,抛开输入是否为零,生成多项式是否为零的因素不看,正常的完整的输出就应该是n +m -1位,这是后续分析的基础。
2、离散卷积法对于一个一般的111g =,进行离散卷积显然如下图(a )所示,离散卷积的结果长度为7。
但是对于1100g =和2001g =,很多同学就觉得困惑了,因为结果长度不够,不知道该如何合并。


卷积码原理举例Convolutional codes are a type of error-correcting code used in digital communication systems to detect and correct errors that may occur during transmission. They are widely used in various communication systems, such as wireless communication, satellite communication, and digital television.卷积码是一种在数字通信系统中用于检测和纠正传输过程中可能发生的错误的纠错码。
它们被广泛应用于各种通信系统,如无线通信、卫星通信和数字电视。
The basic principle behind convolutional codes is to introduce redundancy into the transmitted data in such a way that errors can be detected and corrected at the receiver end. This is achieved by encoding the data using a convolutional encoder, which generates a sequence of output symbols based on the input data.卷积码背后的基本原理是在传输的数据中引入冗余,以便在接收端检测和纠正错误。
这是通过使用卷积编码器对数据进行编码来实现的,该编码器根据输入数据生成一系列输出符号。
One way to understand how convolutional codes work is to think of them as a form of forward error correction, where redundant information is added to the original data before transmission. This redundant information allows the receiver to identify and correct errors that may have occurred during transmission, improving the overall reliability of the communication system.理解卷积码如何工作的一种方法是将其视为一种前向纠错码,即在传输之前向原始数据添加冗余信息。
§4多进制卷积码● 对于q 进制,例如 q =2 n ,——编码产生一个q 进制的序列由处理二进制的R=k/n 的编码器一个单个q 进制符号如:由R =1/3 的二进制编码器8 进制GF (8)中的符号一一对应● R=k/n 存储级数为m 的q 进制卷积码编码器 的构成① k 个并联的q进制寄存器,时延K i ,i =0,1,…,k –1,m =max K i② n 个GF (q )上的加法器③ 乘法器——(系数)由GF (q )中元素加权,描述每个消息符号对第p 个加法器输出的贡献。
● 例1.GF (2k)上的R =1/2、m =1 的卷积码如下图, (K >1),)2(,,)1()0(kj j j GF x x u ∈],1[],1,1[10α==G G或 D D g D D g α+=+=1)(,1)()1(0)0(0ju )0(j x )1(j x● 例2 2-4进制变换卷积编码器(m = 2)§5.恶性卷积码及译码的错误扩展● 例:考虑下面的卷积码编码器)1(j x )1()0(D g j +=)(2)1(D D g j +=1s 2s )4()0(GF x j ∈1(GF ju由于:当u = (0,0,… ,0)x =(00 00 … 00)状态(00) 当u = (1,1,… , 1)x =(00 00 … 00)状态(11) 导致:假设译码时到了状态(01)收的序列为(11 01 00 00 00 … 00) 译码: 1 1 1 1 1… 1 最大似然(d =0) 但实际发 01 00 00 00 00 … 00 ——(d =2) 信道使得错2-比特导致一大串错甚至无限扩展 这种卷积码——恶性卷积码定义:若卷积编码使得译码具有错误的无限扩展性, 则称此卷积码为恶性卷积码定理:若卷积码的(n ,k ,m )的生成多项式)(,),(),(21D g D g D g n ,都是常数项为1的m 次多项式(m ≥1),则该卷积码为恶性卷积码的 充要条件是:)(D g j (j = 1,2,n )有一个非常数公因式。