计量经济学自相关

计量经济学第六章自相关自相关是计量经济学中一种重要的现象，它指的是一个变量与其自己在过去时间点上的相关性。

自相关在实证研究中十分常见，对经济学家来说，了解和掌握自相关性质是至关重要的。

1. 引言自相关作为计量经济学的一项基础概念，是经济学研究中不可或缺的一个重要方法。

自相关性的存在通常会引起回归结果的偏误，而忽略自相关性可能导致估计不准确的结果。

因此，探讨自相关性的性质和应对方法是计量经济学的重点之一。

2. 自相关的定义和表示自相关是指一个变量与其自身在过去时间点上的相关性。

假设我们有一个时间序列数据集，其中变量yt表示一个时间点上的观测值，t表示时间索引。

自相关系数可以通过计算观测值yt与其在过去某一时间点上的观测值yt-k（k为时间滞后期数）的相关性来得到。

数学上，自相关系数可以用公式表示为：ρ(k) = Cov(yt, yt-k) / (σ(yt) * σ(yt-k))其中，ρ(k)表示第k期的自相关系数，Cov表示协方差，σ表示标准差。

3. 自相关性的性质自相关性具有以下几个性质：3.1 一阶自相关性一阶自相关性是指变量值yt与前一期的观测值yt-1之间的相关性。

一阶自相关系数ρ(1)通常用来检验时间序列数据是否存在自相关性。

若ρ(1)大于零且显著，则表明存在正的一阶自相关性；若ρ(1)小于零且显著，则表明存在负的一阶自相关性。

3.2 高阶自相关性除了一阶自相关性，时间序列数据还可能存在高阶自相关性。

高阶自相关性是指变量值yt与过去第k期的观测值yt-k之间的相关性。

通过计算不同滞后期的自相关系数ρ(k)，可以了解数据在不同时间跨度上的自相关性情况。

3.3 异方差自相关性异方差自相关性是指时间序列数据中的方差不仅与自身相关，还与过去观测值的相关性有关。

异方差自相关性可能导致在回归分析中的标准误差失效，从而产生无效的回归结果。

因此，在处理存在异方差自相关性的数据时要采取合适的修正方法。

4. 自相关性的检验方法在实证研究中，经济学家通常使用多种方法来检验数据中的自相关性，常用的方法包括：4.1 Durbin-Watson检验Durbin-Watson检验是一种常用的检验自相关性的方法，其基本思想是通过检验误差项的相关性来判断自相关是否存在。

第六章自相关实验报告一、研究目的对于广大的中国农村人口而言，其消费总量比重却不高。

农村居民的收入和消费是一个值得研究的问题。

消费模型是研究居民消费行为的常用工具。

通过中国农村居民消费模型的分析可判断农村居民的边际消费倾向，这是宏观经济分析的重要参数。

同时，农村居民消费模型也能用于农村居民消费水平的预测。

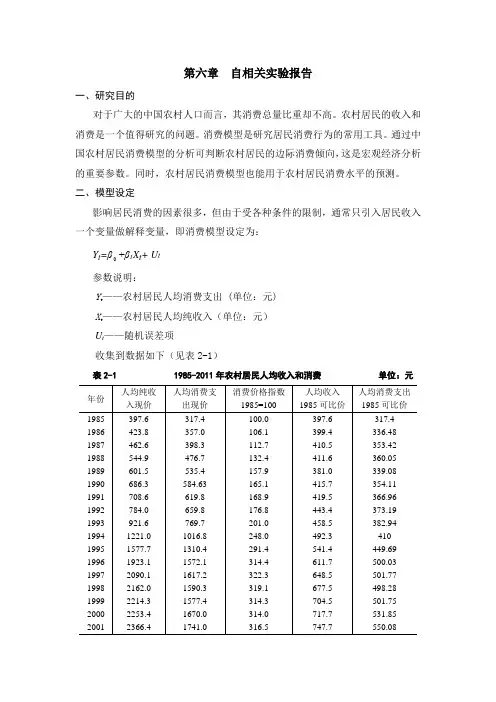
二、模型设定影响居民消费的因素很多，但由于受各种条件的限制，通常只引入居民收入一个变量做解释变量，即消费模型设定为：+β1X t+ U tY t=β参数说明：Y——农村居民人均消费支出 (单位：元)tX——农村居民人均纯收入（单位：元）tU t——随机误差项收集到数据如下（见表2-1）表2-1 1985-2011年农村居民人均收入和消费单位：元注：资料来源于《中国统计年鉴》1986-2012。

为了消除价格变动因素对农村居民收入和消费支出的影响，不宜直接采用现价人均收入和现价人均消费支出的数据，而需要用经消费价格进行调整后的1985年可比价格及人均纯收入和人均消费支出的数据做回归分析。

根据表2-1中调整后的1985年可比价格计的人均纯收入和人均消费支出的数据，使用普通最小二乘法估计消费模型得如下结果。

表2-2 最小二乘估计结果Dependent Variable: YMethod: Least SquaresDate: 12/04/13 Time: 20:00Sample: 1985 2011Included observations: 27Coefficient Std. Error t-Statistic Prob.C 45.40225 10.30225 4.407025 0.0002X 0.718526 0.012526 57.36069 0.0000R-squared 0.992459 Mean dependent var 580.5296 Adjusted R-squared 0.992157 S.D. dependent var 256.4506 S.E. of regression 22.71079 Akaike info criterion 9.154744 Sum squared resid 12894.50 Schwarz criterion 9.250732 Log likelihood -121.5890 Hannan-Quinn criter. 9.183287 F-statistic 3290.249 Durbin-Watson stat 0.528075 Prob(F-statistic) 0.000000由以上结果得到以下方程:^Y t=45.4022545+0.718526X t（6.1）（10.30225）（0.012526）t = (4.407025) (57.36069)R2=0.992459--R2=0.992157 F=3290.249 DW=0.528075该回归方程可决系数较高，回归系数均显著。

计量经济学实验报告(多元线性回归自相关 )1. 背景计量经济学是一门关于经济现象的定量分析方法研究的学科。

它的发展使得我们可以对经济现象进行更加准确的分析和预测，并对社会发展提供有利的政策建议。

本文通过对多元线性回归模型和自相关模型的实验研究，来讨论模型的建立与评价。

2. 多元线性回归模型在多元线性回归模型中，我们可以通过各个自变量对因变量进行预测和解释。

例如，我们可以通过考虑家庭收入、年龄和教育程度等自变量，来预测某个家庭的消费水平。

多元线性回归模型的一般形式为：$y_i=\beta_0+\beta_1 x_{i1}+\beta_2 x_{i2}+...+\beta_k x_{ik}+\epsilon_i$在建立模型之前，我们需要对因变量和自变量进行观测和测算。

例如，我们可以通过调查一定数量的家庭，获得他们的收入、年龄、教育程度和消费水平等数据。

接下来，我们可以通过多元线性回归模型，对家庭消费水平进行预测和解释。

在实际的研究中，我们需要对多元线性回归模型进行评价。

其中一个重要的评价指标是 $R^2$ 值，它表示自变量对因变量的解释程度。

$R^2$ 值越高，说明多元线性回归模型的拟合程度越好。

3. 自相关模型在多元线性回归模型中，我们假设各个误差项之间相互独立，即不存在自相关性。

但实际上，各个误差项之间可能会互相影响，产生自相关性。

例如，在一个气温预测模型中，过去的温度对当前的温度有所影响，说明当前的误差项和过去的误差项之间存在相关性。

我们可以通过自相关函数来研究误差项之间的相关性。

自相关函数表示当前误差项和过去 $l$ 期的误差项之间的相关性。

其中，$l$ 称为阶数。

自相关函数的一般形式为：$\rho_l={\frac{\sum_{t=l+1}^{T}(y_t-\bar{y})(y_{t-l}-\bar{y})}{\sum_{t=1}^{T}(y_t-\bar{y})^2}}$在自相关模型中，我们通过对误差项进行差分或滞后变量，来消除误差项之间的自相关性。

《计量经济学》中多重共线性、异方差性、自相关三者之间的联系与区别首先我们先来回顾一下经典线性回归模型的基本假设：1、为什么会出现异方差性我们可以从一下两方面来分析：第一，因为随即误差项包括了测量误差和模型中被省略的一些因素对因变量的影响；第二，来自不同抽样单元的因变量观察值之间可能差别很大。

因此，异方差性多出现在截面样本之中。

至于时间序列，则由于因变量观察值来自不同时期的同一样本单元，通常因变量的不同观察值之间的差别不是很大，所以异方差性一般不明显。

含义及影响:y=X β+ε，var(εi )var(εj ), ij ，E(ε)=0，或者记为212200['|]0000n E X σεεσσ⎛⎫⎪=Ω= ⎪ ⎪⎝⎭即违背假设3。

用OLS 估计，所得b 是无偏的，但不是有效的。

111(')'(')'()(')'b X X X y X X X X X X X βεβε---==+=+由于E(ε)=0，所以有E(b )=β。

即满足无偏性。

但是，b 的方差为1111121var(|)[()()'][(')''(')|] (')'['|](') (')'()(')b X E b b E X X X X X X X X X X E X X X X X X X X X X ββεεεεσ------=--===Ω其中212200['|]0000n E X σεεσσ⎛⎫⎪=Ω= ⎪ ⎪⎝⎭2、自相关产生的原因：（1）、经济数据的固有的惯性带来的相关 （2）、模型设定误差带来的相关 （3）、数据的加工带来的相关 含义及影响:cov(,)0,i j i j εε≠≠影响：和异方差一样，系数的ls 估计是无偏的，但不是有效的。

D －W 检验（Durbin －Watson ）221212222121212222112112122211221122121()()()2()()222222(1)n i i i n i i n n n i i i i i i i n i i n n n i i i i i i i n n i i n i i i nn n i i i i nn i ie e d e e e e e e e e e e e e e e e e e e e e e e ρρ=-===-=-====-==-===∑-=∑∑+∑-∑=∑∑+∑-∑--=∑∑+=--∑∑+=--∑≈-其中2121n i i i n i ie e e ρ=-=∑=∑是样本一阶自相关函数。

第六章自相关性6.1 自相关性：6.1.1. 非自相关假定由第2章知回归模型的假定条件之一是，Cov(u i, u j) = E(u i u j) = 0, (i, j∈T, i≠j), (6.1)即误差项u t的取值在时间上是相互无关的。

称误差项u t非自相关。

如果Cov (u i,u j ) ≠ 0, (i≠j)则称误差项u t存在自相关。

自相关又称序列相关。

原指一随机变量在时间上与其滞后项之间的相关。

这里主要是指回归模型中随机误差项u t与其滞后项的相关关系。

自相关也是相关关系的一种。

6.1.2．一阶自相关自相关按形式可分为两类。

(1)一阶自回归形式当误差项u t只与其滞后一期值有关时，即u t = f (u t - 1) + v t称u t具有一阶自回归形式。

(2) 高阶自回归形式当误差项u t的本期值不仅与其前一期值有关，而且与其前若干期的值都有关系时，即u t = f (u t– 1, u t– 2 , …u t– p ) + v t则称u t具有P阶自回归形式。

通常假定误差项的自相关是线性的。

因计量经济模型中自相关的最常见形式是一阶自回归形式，所以下面重点讨论误差项的线性一阶自回归形式，即u t = α1 u t -1 + v t(6.2)其中α1是自回归系数，v t 是随机误差项。

v t 满足通常假设E(v t) = 0, t = 1, 2 …,T,Var(v t) = σv2, t = 1, 2 …,T,Cov(v i , v j ) = 0, i ≠ j , i , j = 1, 2 …, T , Cov(u t -1, v t ) = 0, t = 1, 2 …, T ,依据普通最小二乘法公式，模型（6.2）中 α1 的估计公式是，1ˆa= ∑∑=-=-Tt t Tt t t u u u 22121(1ˆβ=∑---2)())((x x x x y y t t t ) (6.3)其中T 是样本容量。

实验6.美国股票价格指数与经济增长的关系——自相关性的判定和修正一、实验内容：研究美国股票价格指数与经济增长的关系。

1、实验目的:练习并熟练线性回归方程的建立和基本的经济检验和统计检验；学会判别自相关的存在，并能够熟练使用学过的方法对模型进行修正。

2、实验要求：（1）分析数据，建立适当的计量经济学模型（2）对所建立的模型进行自相关分析（3）对存在自相关性的模型进行调整与修正二、实验报告1、问题提出通过对全球经济形势的观察，我们发现在经济发达的国家，其证券市场通常也发展的较好，因此我们会自然地产生以下问题，即股票价格指数与经济增长是否具有相关关系？GDP是一国经济成就的根本反映。

从长期看，在上市公司的行业结构与国家产业结构基本一致的情况下，股票平均价格的变动跟GDP的变化趋势是吻合的，但不能简单地认为GDP 增长，股票价格就随之上涨，实际走势有时恰恰相反。

必须将GDP与经济形势结合起来考虑。

在持续、稳定、高速的GDP增长下，社会总需求与总供给协调增长，上市公司利润持续上升，股息不断增加，老百姓收入增加，投资需求膨胀，闲散资金得到充分利用，股票的内在含金量增加，促使股票价格上涨，股市走牛。

本次试验研究的1970-1987年的美国正处在经济持续高速发展的状态下，据此笔者利用这一时期美国SPI与GDP的数据建立计量经济学模型，并对其进行分析。

2、指标选择：指标数据为美国1970—1987年美国股票价格指数与美国GDP数据。

3、数据来源：实验数据来自《总统经济报告》（1989年），如表1所示：表1 4、数据处理将两组数据利用Eviews绘图，如图1、2所示：图1 GDP数据简图图2 SPI数据简图经过直观的图形检验，在1970-1987年间，美国的GDP保持持续平稳上升，SPI虽然有些波动，但波动程度不大，和现实经济相符，从图形上我们并没有发现有异常数据的存在。

所以可以保证数据的质量是可以满足此次实验的要求。

计量经济学第六章自相关在计量经济学的学习中，自相关是一个重要且颇具挑战性的概念。

自相关，简单来说，就是指在时间序列或横截面数据中，观测值之间存在的某种相关性。

想象一下，我们在研究某个经济变量随时间的变化情况，比如一家公司的销售额。

如果在不同的时间段，销售额的变化不是相互独立的，而是存在一定的关联，这就可能出现了自相关现象。

自相关产生的原因多种多样。

其中一个常见的原因是经济变量的惯性。

例如，消费者的消费习惯往往具有一定的延续性，不会突然发生巨大的改变。

这就导致消费数据在不同时期可能存在相关性。

另一个可能的原因是模型设定的不准确。

如果我们在构建计量经济模型时，遗漏了某些重要的解释变量，那么残差项就可能包含这些被遗漏变量的影响，从而导致自相关。

自相关的存在会给我们的计量经济分析带来一系列问题。

首先，它会影响参数估计的有效性。

在存在自相关的情况下，传统的最小二乘法（OLS）估计得到的参数估计值不再是最优的，估计的方差也会被低估，这可能导致我们对参数的显著性做出错误的判断。

其次，自相关会使我们对模型的假设检验失效。

假设检验是基于一定的统计分布进行的，如果存在自相关，这些分布就不再适用，从而导致检验结果的不可靠。

那么，如何检测自相关呢？常用的方法有图形法、杜宾瓦特森（DurbinWatson）检验等。

图形法是通过绘制残差的序列图来直观地观察是否存在自相关。

如果残差呈现出某种周期性或趋势性，那么就可能存在自相关。

杜宾瓦特森检验则是一种基于统计量的检验方法。

它通过计算一个特定的统计量，并与临界值进行比较来判断是否存在自相关。

如果经过检测发现存在自相关，我们就需要采取相应的方法来处理。

一种常见的方法是广义最小二乘法（GLS）。

GLS通过对原模型进行变换，使得变换后的模型不存在自相关，从而得到更有效的参数估计。

另外，还可以使用一阶差分法。

这种方法将原变量的一阶差分作为新的变量进行回归分析，从而消除可能存在的自相关。

第6章 自相关6.1 复习笔记考点一：什么是自相关 ★★★1．自相关的概念自相关又称序列相关，是指总体回归模型的随机误差项u i 之间存在相关关系的一种现象。

在古典假定中假设随机误差项是无自相关的，即：Cov （u i ，u j ）＝E （u i u j ）＝0（i ≠j ）。

如果该假定不能满足，就称u i 与u j 存在自相关，即不同观测点上的误差项彼此相关。

自相关系数可用来表示自相关的程度。

随机误差项u t 与滞后一期的u t －1的自相关系数ρ的计算公式为：1nt t u uρ-=∑式中u t －1是u t 滞后一期的随机误差项，因此上式计算的自相关系数ρ称为一阶自相关系数。

自相关系数ρ的取值范围为－1≤ρ≤1。

如果ρ＜0，则u t 与u t －1间存在负相关关系；如果ρ＞0，则u t 与u t －1间存在正相关关系；如果ρ＝0，则u t 与u t －1不相关。

2．自相关产生的原因（见表6-1）表6-1 自相关产生的原因自相关关系主要存在于时间序列数据中，但是在横截面数据中也可能会出现，通常称横截面数据中出现的自相关为空间自相关。

多数经济时间序列在较长时间内都表现为上升或下降的趋势，因此大多表现为正自相关。

但就自相关本身而言，既有正相关也有负相关。

3．自相关的表现形式（1）一阶自相关随机误差项的一阶自相关形式为：u t＝ρu t－1＋v t（－1＜ρ＜1）。

其中，ρ为自相关系数；v t为满足古典假定的误差项，即E（v t）＝0，Var（v t）＝σ2，Cov（v t，v t＋s）＝0，s ≠0。

一阶自回归形式记为AR（1），相应的式中的ρ称为一阶自相关系数。

（2）m阶自相关如果一阶自相关中的随机误差项v t是不满足古典假定的误差项，即v t中包含有u t的成分，如包含有u t－2，…，u t－m的影响，则需将u t－2，…，u t－m包含在回归模型中，即：u t＝ρ1u t －1＋ρ2u t －2＋…＋ρm u t －m ＋v t 。