具有时变时滞和未建模动态的不确定非线性系统自适应控制研究

《无模型自适应控制方法综述》在现代控制领域中，无模型自适应控制方法因其独特的优势和广泛的应用前景而备受关注。

随着科技的不断发展和工业生产等领域对控制性能要求的日益提高，无模型自适应控制方法逐渐成为解决复杂系统控制问题的重要手段之一。

本文旨在对无模型自适应控制方法进行全面而系统的综述，深入探讨其基本原理、主要类型、特点以及在实际应用中的成果和挑战。

一、概述控制系统在工业生产、航空航天、交通运输、自动化等众多领域中起着至关重要的作用。

传统的控制方法往往基于对被控对象精确的数学模型建立，但在实际系统中，由于系统的复杂性、不确定性以及建模误差等因素的存在，很难获得准确且精确的数学模型。

这就促使了无模型自适应控制方法的产生和发展。

无模型自适应控制方法不依赖于被控对象的精确数学模型，而是通过对系统的上线观测和学习，不断调整控制策略，以适应系统的变化和不确定性，从而实现对被控对象的良好控制。

二、无模型自适应控制方法的基本原理无模型自适应控制方法的基本原理可以概括为以下几个关键步骤：（一）系统上线观测与状态估计通过传感器等手段对被控系统的状态变量进行实时监测和采集，获取系统的当前状态信息。

然后利用合适的估计方法，如卡尔曼滤波等，对系统的状态进行估计，以获得更准确的系统状态表征。

（二）控制律设计基于估计的系统状态，设计相应的控制律。

控制律的设计通常是根据一定的性能指标和控制策略进行优化，以实现对被控系统的期望控制效果。

（三）自适应调整根据系统的实际运行情况和估计误差，不断调整控制律中的参数或结构，使控制系统能够自适应地适应系统的变化和不确定性。

这种自适应调整可以是基于模型的自适应，也可以是基于数据驱动的自适应等方式。

通过以上基本原理的循环迭代，无模型自适应控制方法能够逐步逼近系统的最优控制状态，实现对被控系统的有效控制。

三、无模型自适应控制方法的主要类型（一）模型参考自适应控制（MRAC）MRAC 是无模型自适应控制中最经典的一种方法。

先进控制技术综述1 引言在实际的工业控制过程中，很多系统具有高度的非线性、多变量耦合性、不确定性、信息不完全性和大滞后等特性。

对于这种系统很难获得精确的数学模型，并且常规的控制无法获得满意的控制效果。

面对这些复杂的工业控制产生了新的控制策略，即先进控制技术。

先进控制技术包括：自适应控制，预测控制，推理控制，鲁棒控制以及包括模糊控制与神经网络在内的智能控制方法。

本文详细介绍了自适应控制、预测控制以及这两种先进控制的应用领域和优缺点[1]。

2 自适应控制自适应控制的思想是对于系统中的不确定性，以及控制任务的艰巨性，对于部分未建模的动态特性、变化的被控对象和干扰信号，及时地测得它们的信息，并根据此信息按一定的设计方法，自动地做出控制决策、修改控制器结构和参数，使其控制信号能够适应对象和扰动的动态变化，在某种意义上达到控制效果最优或次优。

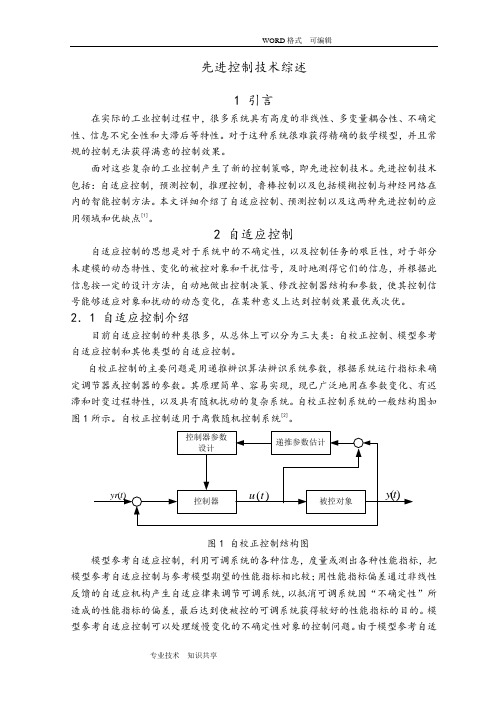
2．1 自适应控制介绍目前自适应控制的种类很多，从总体上可以分为三大类：自校正控制、模型参考自适应控制和其他类型的自适应控制。

自校正控制的主要问题是用递推辨识算法辨识系统参数，根据系统运行指标来确定调节器或控制器的参数。

其原理简单、容易实现，现已广泛地用在参数变化、有迟滞和时变过程特性，以及具有随机扰动的复杂系统。

自校正控制系统的一般结构图如图1所示。

自校正控制适用于离散随机控制系统[2]。

图1 自校正控制结构图模型参考自适应控制，利用可调系统的各种信息，度量或测出各种性能指标，把模型参考自适应控制与参考模型期望的性能指标相比较；用性能指标偏差通过非线性反馈的自适应机构产生自适应律来调节可调系统，以抵消可调系统因“不确定性”所造成的性能指标的偏差，最后达到使被控的可调系统获得较好的性能指标的目的。

模型参考自适应控制可以处理缓慢变化的不确定性对象的控制问题。

由于模型参考自适应控制可以不必经过系统辨识而度量性能指标，因而有可能获得快速跟踪控制。

模型参考自适应控制结构框图如图2所示，模型参考自适应控制一般用于确定性连续控制系统。

具有输入未建模动态的纯反馈非线性系统自适应控制张天平;葛继伟;夏晓南【摘要】对一类具有状态和输入未建模动态且控制增益符号未知的纯反馈非线性系统,利用非线性变换、改进的动态面控制方法以及Nussbaum函数性质,提出两种自适应动态面控制方案.利用正则化信号来约束输入未建模动态,从而有效地抑制其产生的扰动.通过引入动态信号,有效地处理了由状态未建模动态引起的动态不确定性.通过在总的李雅普诺夫函数中引入非负正则化信号,并利用稳定性分析中引入的紧集,证明了闭环控制系统是半全局一致终结有界的.数值仿真验证了所提方案的有效性.%Based on dynamic surface control(DSC)method and using Nussbaum function property,two adaptive DSC schemes are developed for a class of pure-feedback nonlinear systems with state and input unmodeled dynamics as well as unknown control gain sign in this paper.Normalization signal is designed to restrict the input unmodeled dynamics, and the disturbance produced by it is effectively suppressed.Dynamic signal is introduced to deal with the dynamic uncertainty caused by unmodeled dynamics.By adding the normalization signal to the whole Lyapunov function and using the defined compact set in stability analysis,all the signals in the closed-loop system are proved to be semi-globally uniformly ultimately bounded(SGUUB).Numerical simulation verifies the effectiveness of the proposed approach.【期刊名称】《控制理论与应用》【年(卷),期】2017(034)012【总页数】11页(P1637-1647)【关键词】输入未建模动态;动态面控制;积分型Lyapunov函数;Nussbaum函数【作者】张天平;葛继伟;夏晓南【作者单位】扬州大学信息工程学院自动化专业部,江苏扬州225127;扬州大学信息工程学院自动化专业部,江苏扬州225127;扬州大学信息工程学院自动化专业部,江苏扬州225127【正文语种】中文【中图分类】TP131 引言(Introduction)自从文献[1]提出后推设计以来,它已成为非线性系统控制的主要设计工具.其缺点是在后推的每一步需对虚拟控制反复求导,随着系统阶次的增加,控制器的结构越加复杂,通常称为“微分爆炸”问题.文献[2]通过在后推的每一步引入一个1阶滤波器,用代数运算代替微分运算来消除传统后推设计的不足.文献[3–4]在文献[2]基础上分别对严格反馈及纯反馈两类非线性系统提出两种自适应动态面控制方案.进一步,文献[5]提出一种改进的动面控制策略.近年来,带有输入未建模动态的自适应控制受到了人们广泛的关注,并取得了一些研究成果.文献[6]首次对输入未建模动态展开了研究,并分别对具有线性输入未建模动态的严格反馈非线性系统和输出反馈非线性系统,利用正则化信号、动态非线性阻尼设计和后推技术,设计了相应的控制律.该设计保证了对于传递函数描述下的输入未建模增益,存在一个独立于初始条件的正则化信号,使得系统所有输入与状态收敛于一个区间内.文献[7]利用小增益定理拓展了文献[6]关于输入未建模动态的研究思路.文献[8]在文献[6–7]的基础上得到了进一步的结果,证明了未建模动态子系统为零相对阶的最小相位系统的有界性.文献[9–15]关于输入未建模动态展开了不同的讨论.对于线性输入未建模动态,相应的约束条件是子系统为最小相位系统,而对于非线性输入未建模动态,要求子系统零动态是输入状态稳定的.在该假设条件下,根据输入未建模动态李雅普诺夫函数的指数收敛率,设计正则化信号,提出自适应后推控制律,但系统高频增益符号假设是已知的.众所周知,当系统的控制方向未知时常常给控制器的设计带来较大困难.由于具有广阔的应用背景,控制增益符号未知的非线性系统受到广泛的讨论.文献[16]为控制方向未知的系统提供了一种通用性控制方法,即Nussbaum函数增益技术.文献[17–18]针对存在未知高频增益和时变不确定性的非线性系统,利用Nussbaum函数和后推技术,提出了一种鲁棒控制策略.文献[19]利用Nussbaum函数性质讨论了一类具有时滞不确定性的严格反馈系统的自适应控制问题,同时给出了时变控制增益符号未知的闭环系统稳定的判断定理.文献[20]对一类具有未建模动态的纯反馈非线性系统,在虚拟控制增益已知和未知的两种情形下,分别提出了自适应动态面控制方案,并利用Nussbaum函数解决了虚拟控制增益未知的问题.文献[21]对一类具有未建模动态及动态不确定性的严格反馈非线性系统,利用李雅普诺夫函数刻画状态未建模动态,提出一种新的自适应动态面控制方案.文献[22–23]对一类带有输入未建模动态的输出反馈非线性系统,利用正则化信号约束输入未建模动态,提出两种输出反馈自适应动态面控制策略.文献[24]对一类具有未建模动态和死区的纯反馈非线性系统,在假设控制增益符号已知的条件下,提出一种基于改进动态面控制的自适应神经网络控制方案.本文在文献[5,20,22,24]的基础上,对一类纯反馈非线性系统,提出了两种新的鲁棒自适应动态面控制策略.主要贡献如下:1)对同时具有状态和输入未建模动态的非线性系统,分别讨论了控制增益gn(x)符号已知和未知两种情况,提出了两种不同的自适应控制策略,而文献[22–23]中讨论的系统是一类输出反馈非线性系统.2)通过非线性变换将纯反馈系统转化为更容易分析的严格反馈系统形式,采用改进的动态面控制方法,避免采用中值定理,从而移去了虚拟控制增益符号及其上下界已知的假设条件,并简化了设计.3)在后推设计的前n−1步仅有一个参数需要在线调节,减轻了计算量.4)通过在总的李雅普诺夫函数中加入非负正则化信号,并利用动态面控制证明的特点,有效地处理了控制信号的有界性.2 问题的描述及基本假设(Problem statement and basic assumptions)考虑如下一类具有输入未建模动态的纯反馈非线性系统:式中:i=[x1x2···xi]T∈Ri,i=1,2···,n;x=[x1···xn]∈Rn是状态向量,ω∈R是作用在非线性系统上的不可量测信号,y∈R是系统输出,gn(x),fi(·)(i=1,···,n)是未知光滑函数,z∈ Rn0是不可测量状态,∆i(t,z,x)(i=1,···,n)为未知不确定扰动.输入未建模子系统描述如下:式中:p∈Rn1是由输入u∈R所产生的未建模状态,ω∈ R是n1阶子系统的输出,A∆(·)和b∆是未知向量,c∆(·)是未知函数并且d∆未知常数.控制目标:设计自适应控制律u,使得系统的输出y尽可能好地跟踪一个给定的期望信号yd,并保证闭环系统是半全局一致终结有界的,且跟踪误差收敛到一个小的残差集内.定义1[25]对于系统=q(t,z,x),如果存在K∞类函数1,2和一个Lyapunov函数V0(z)使得以及存在两个常数c＞0,d≥0和一个K∞类函数γ(·)使得式中:c＞0,d≥0是两个已知常数,γ(·)是一个已知K∞类函数,则称未建模动态是指数输入状态实用稳定(exponentially input-state-practically stable,exp-ISpS).假设1[25]未建模动态是指数输入状态实用稳定(exp-ISpS)的.假设2 gn(x)的符号是已知的,且存在常数gi0和gn1,使得不失一般性,假设gn(x)＞0.假设3[3]期望轨迹向量xd=[yddd]T∈Ωd连续可测,其中是一个紧集,B0是一个已知正常数.假设4[25]对未知不确定扰动∆i(t,z,x),i=1,···,n,存在未知非负连续函数ρi1(·),未知非负连续单调递增函数ρi2(·),使得其中‖·‖表示欧氏范数.假设5[13] 对于输入未建模动态子系统(2)–(3),其相对阶数为零,即d∆̸=0,且存在一个常数,使得‖c∆(p)‖≤‖p‖.假设6[13] 对于输入未建模动态子系统(2)–(3),存在一个Lyapunov函数W(p),满足式中:βp1,βp2,βp3是正常数,δ0是已知正常数.引理1[25]若V0(t)是系统=q(t,z,x)的一个exp-ISpS李雅普诺夫函数,即假设1成立,则对于任意常数f∈(0,c),任意初始时间t0＞0,任意初始状态z0=z(t0),v0＞0和任意(|x1|)≥γ(|x1|),存在有限时间对于非负函数D(t0,t),定义动态信号=−fv+(|x1|)+d.当t≥ t0+T0时,存在D(t0,t)=0,使得V0(z)≤v(t)+D(t0,t).不失一般性,取(|x1|)=γ(|x1|).引理2若假设6成立,=−δ0+|u|,则存在常数c1,c2＞0使得其中δ0由式(7)确定.引理2证明参见文献[13].注1 假设1是对未建模动态的要求;假设2是为了保证所讨论的下三角型系统是能控的而对未知系统函数提出的基本要求;假设3是对跟踪信号的要求;假设4是对动态不确定性提出的要求;假设5–6是对输入未建模动态的刻画.假设1–6在现有文献中已被广泛使用.仿真中应该验证状态未建模动态和输入未建模动态满足假设1,4–6.此外,需要构造适当的李雅普诺函数,如来确定设计动态信号、正则化信号用到的设计参数f及δ0.3 控制增益符号已知的控制器设计(Controller design with known gain sign) 本节中,首先讨论系统控制增益gn(x)及d∆符号已知的情形,不妨假设全为正.令Fi(i,xi+1)=fi(i,xi+1)−xi+1,i=1,···,n−1.则系统(1)可改写为如下形式:对于未知连续函数Fi(i,xi+1),1≤i≤n−1,在给定的紧集ΩZi上,本文将采用径向基函数神经网络进行逼近,即式中:Zi=i+1,εi(Zi)是逼近误差,i=1,···,n−1,Fn(Zn)将在最后一步中给出,Zn=[xTsnnv]T.基向量ξi(Zi)=[ξi1(Zi) ···ξili(Zi)]T∈ Rli,基函数定义如下:其中:bik和aik分别为高斯函数的中心和宽度,k=1,···,li,理想权向量定义为控制器设计分为n步,βi是以αi为输入的一阶滤波器的输出,i=2,···,n.最后,控制律u 将在第n步提出.为了叙述方便,定义一些如下形式的Lyapunov函数:式中:s1=x1−β1=y−yd,si=xi−βi,i=2,···,n.第1步由式(10)可知对s1求导得设计虚拟控制律α2如下:式中:a1＞0,k1＞0是设计常数,是λ在t时刻的估计,而设计一阶滤波器如下:式中:τ2为时间常数,α2为系统输入,β2为系统状态.令y2=β2−α2,可得出因此有式中是一个非负连续函数.对Vs1关于时间t求导,得式中=−λ.由假设4和引理1可知存在一个正常数D0,使得D(t0,t)≤ D0,∀t≥ 0,可得式中:表示由Young’s不等式得将式(25)–(26)代入式(24),可得式中:是一个未知的非负连续函数.第i步(2≤i≤n−1) 对si求导得设计虚拟控制律αi+1如下:式中:ai＞0,ki＞0是设计常数.设计一阶滤波器如下:式中:τi+1为时间常数.令yi+1= βi+1− αi+1,可得进一步有类似于第1步的推导,易得式中:是一个未知的非负连续函数.第n步令sn=xn−βn,因此可得令Gn(x)=d∆gn(x),定义一个光滑Lyapunov函数如下:由积分第2中值定理可知其中σ∈(0,1).因此Vsn为正定函数.将Vsn对时间t求导并利用分部积分可得由假设4得同理,与第1步类似,由假设4和引理1可得由Young’s不等式可得由假设4和引理1,可得式中对于未知连续函数Fn(Zn),在给定的紧集ΩZn上采用径向基函数神经网络进行逼近,即将式(33)(36)–(41)代入式(35),可得将式(3)代入式(42),并利用Young’s不等式,可得为了处理上式中项,由假设5–6及引理2可知设H=max{c1(‖p(0)‖+|(0)|),c2},则可得不妨令将其代入上式,可得式中P=(1+|(t)|)2.设计下面的控制律u:式中:an＞0,kn＞0是设计常数,是H在t时刻的估计.将式(46)和式(47)代入式(43),并利用Young’s不等式,可得式中:是一个未知的非负连续函数,设计参数,的自适应调节律如下:式中γ1,γ2,σ1,σ2＞ 0是设计常数.定义紧集式中:γ3＞0是一个设计常数,J为任给的正常数,pn=2n+3.令连续函数κi在紧集Ωn×Ωd上的最大值为M1i(i=1,···,n),ηi在紧集Ωn×Ωd上的最大值为M2i(i=2,···,n),|u|在紧集Ωn×Ωd上的最大值为M3.定理1 考虑由系统(1)、控制律(47)、自适应律(49)–(50)组成的闭环系统,若假设(1)–(6)成立,对于任意有界初始条件及V(0)≤J,存在常数ki,τi,γ1,γ2,σ1,σ2使得闭环系统半全局一致终结有界,其中ki,1/τi,α0满足如下条件:证选取如下Lyapunov函数:将V对时间t求导,可得所以当V≤J时,易得将式(52)代入式(55),可得当V≤J,可得有界.因为x1=s1+yd,xi=si+yi+ αi,利用式(20)–(30),依次可得x1,α2,x2,···,αn,xn是有界的.由∈L∞,可得P是有界的.根据式(47)及,,P∈L∞,可得u∈L∞.因为Q(n−1,v)是一个非负连续函数,n−1,v有界,所以Q(n−1,v)有界.可设Q(n−1,v)≤µ0,µ0是正常数.由上式可得如果V=J且α0≥(µ0+µ1)/J,那么≤0.进一步,如果V(0)≤ J,那么V(t)≤ J,∀t＞ 0.式(57)两边同乘以eα0t可得对式(58)积分,可得因此,闭环系统的所有信号和是一致终结有界的.进一步有xi,yi+1和αi,u一致终结有界.4 控制增益符号未知的控制器设计(Controller design with unknown gain sign) 本节中,将放宽假设条件,研究含有Nussbaum函数的自适应动态面控制器来处理控制增益符号未知且具有输入未建模动态情形的控制问题.假设7 gn(x)的符号是未知的,且存在常数gi0和gn1,使得其中Nussbaum函数性质如下:常用的Nussbaum函数包括:和本文选取引理 3 已知V(·),ζ(·)都是[0,tf)上的光滑函数,且V(t)≥ 0,∀t∈ [0,tf),N(·)是一个Nussbaum函数,如果下列不等式成立其中:c为非负常数,g(x(τ))是一个在闭区间[l−,l+]取值的时变参数,α是一个正常数.可得V(t),ζ(t)和一定在[0,tf)上有界.第i步(0≤i≤n−1) 与第3节讨论相同,在此不再赘述.第n步令sn=xn−βn,因此可得由假设7,定义一个光滑Lyapunov函数如下:由积分第2中值定理可知,Vsn可改写为其中σ∈(0,1).对Vsn在时间t上求导,可得类似于第3节的推导,易得设计控制律如下:令类似于式(44)–(45)的推导,可得将式(68)–(70)代入式(68),并利用Young’s不等式得定义总的Lyapunov函数如下:式中γ3＞0是设计常数.定义紧集式中:J为任给的正常数,pn=2n+2.令连续函数κi在紧集Ωn×Ωd上的最大值为M1i,i=1,···,n,ηi在紧集Ωn×Ωd上的最大值为M2i,i=2,···,n.定理2 考虑一类由系统(1)、控制律(68)–(69)、自适应律(48)组成的闭环系统,若假设1,3–7成立,则对于任意有界初始条件及V(0)≤J,存在常数ki,τi,γ1,γ2,σ1,σ2使得闭环系统半全局一致终结有界,其中ki,1/τi,α0满足如下条件:证总的Lyapunov函数V由式(72)确定.当V≤J时,对Lyapunov函数V求导并利用式(68)–(69)可得将式(74)代入式(75),可得若V≤J,则有有界,类似于定理1的分析可得n,αi有界.根据∈L∞,可知P有界.因为Q(n−1,v)是一个非负连续函数,n−1,v有界,所以Q(n−1,v)有界.可设Q(n−1,v)≤µ0,µ0是一个未知正常数.由式(78)得类似于第2节的讨论,可得由引理3可知,V(t)和ζ(t)在[0,tf)上有界.由于tf是任意正常数,因此,和ζ(t)在[0,∞)上有界.进一步由式(69)可知,式(77)右边第4项是有界的,即存在正常数µ2使得N(ζn)+1]n|≤ µ2.由式(77)可得如果V=J且α0≥(µ0+µ1+µ2)/J,那么≤0.进一步,如果V(0)≤ J,那么V(t)≤J,∀t≥0.因此,闭环系统的所有信号si,yi,,v,和是一致终结有界的.进一步,可得xi,yi+1和αi,u一致终结有界.注2 本文利用Nussbaum函数,设计了控制律(68)和Nussbaum参数自适应律(69).进一步,在总的李雅普诺夫函数中加入了正则化信号,从而证明了闭环系统的稳定性.5 仿真结果(Simulation results)例1考虑如下具有未建模动态的倒立摆系统[23]:式中:q(t,z,y)= −2z+y sin t+0.5,∆1=0.5z,∆2=x1z,g=9.8 m/s2重力加速度,mc=1kg 是小车的质量,ml=0.1kg是半个杆的质量,l=0.5m是半个杆的长度.期望的轨迹为yd=(π/30)sin t.仿真中,=−δ0+|u|,=−v+2.5y2+0.6;设计参数取为k1=5,k2=10,γ1=γ2=4,σ1= σ2=0.01,δ0=1.5,τ2=0.05;初值为x(0)=[0.05 −0.1]T,z(0)=0,p(0)=[00]T,(0)=1.5,(0)=0.15,(0)=0.2,v(0)=1.5.基向量为仿真结果如图1–3所示.从图1,2可知,本文所设计的自适应控制能够保证闭环系统具有良好的跟踪性能.例2考虑如下一类具有输入和状态未建模动态的纯反馈非线性系统:期望的跟踪轨迹yd(t)=0.5sint+0.25sin(0.5t).图1 增益符号已知的倒立摆系统输出y和期望轨迹ydFig.1 Output y and desired trajectory ydfor inverted pendulum system with known gain sign图2 跟踪误差s1Fig.2 Tracking error s1图3 控制信号uFig.3 Control signal u对于控制方案1(增益符号已知):仿真中动态信号为设计参数取为初值取为神经网络的设计参数为仿真结果如图4–6所示.图4 增益符号已知的纯反馈系统输出y和期望轨迹ydFig.4 Output y and desired trajectory ydfor pure-feedback system with known gain sign 图5 跟踪误差s1Fig.5 Tracking error s1图6 控制信号uFig.6 Control signal u对于控制方案2(增益符号未知):仿真中动态信号为设计参数取为初值取为神经网络的设计参数为仿真结果如图7–9所示.图7 增益符号未知的纯反馈系统输出y和期望轨迹ydFig.7 Output y and desired trajectory ydfor pure-feedback system with unknown gain sign 图8 跟踪误差s1Fig.8 Tracking error s1图9 控制信号uFig.9 Control signal u6 结论(Conclusions)本文对一类具有状态和输入未建模动态的纯反馈非线性系统,利用非线性变换将纯反馈非线性系统转换为形式上的严格反馈非线性系统,进一步,利用动态面控制方法,对控制增益符号已知和未知情况,提出两种自适应控制方案.通过引入一阶滤波器,降低了控制器设计的复杂性.利用径向基函数神经网络逼近系统中的未知光滑非线性函数.利用积分型李雅普诺夫函数放宽了控制增益的要求.利用Young’s不等式,对推导过程中的不确定项进行放缩,从而减少神经网络在线调节参数的数目.利用Nussbaum函数的性质,处理虚拟控制增益符号未知问题.在未来的研究工作中进一步将其结果推广到具有输出和状态约束的非线性系统.参考文献(References):【相关文献】[1]KANELLAKOPOULOS I,KOKOTOVIC P V,MORSE A S.Systematic design of adaptive controllers for feedback linearizable systems[J].IEEE Transactions on Automatic Control,1991,36(11):1241–1253.[2]SWAROOP D,HEDRICK J K,YIP P P,et al.Dynamic surface control for a class of nonlinear systems[J].IEEE Transactions on Automatic Control,2000,45(10):1893–1899.[3]WANG D,HUANG J.Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strictfeedback form[J].IEEE Transactions on Neural Networks,2005,16(1):195–202.[4]ZHANG T P,GE S S.Adaptive dynamic surface control of nonlinear systems with unknown dead zone in pure feedback form[J].Automatica,2008,44(7):1895–1903.[5]WANG D.Neural network-based adaptive dynamic surface control of uncertain nonlinear pure-feedback systems[J].International Journal of Robust and Nonlinear Control,2011,21(5):527–541.[6]KRSTIC M,SUN J,KOKOTOVIC P V.Robust control of nonlinear systems with input unmodeled dynamics[J].IEEE Transactions on Automatic Control,1996,41(6):913–920. [7]JIANG Z P,MAREELS I,POMETS J B.Controlling nonlinear systems with input unmodeleddynamics[C]//Proceedings of the 35th IEEE Conference on Decision and Control.New York:IEEE,1996:805–806.[8]ARCAKM,KOKOTOVICP.Furtherresultsonrobustcontrolofnonlinear systems with input unmodeled dynamics[C]//Proceedings of the American Control Conference.NewYork:IEEE,1999:4061–4065.[9]JANKOVIC M,SEPULCHR R,KOKOTOVIC P V.CLF based designs with robustness to dynamic input uncertainties[J].Systems and Control Letter,1999,37(1):45–54.[10]JIAOX,SHENT,TAMURAK.Passivity-basedrobustfeedbackcontrol for nonlinear systems with input dynamical uncertainty[J].International Journal of Control,2004,77(6):517–526.[11]JIANG Z P,ARCAK M.Robust global stabilization with input unmodeled dynamics:an ISS small-gain approach[C]//Proceedings of the 39th IEEE Conference on Decision and Control.New York:IEEE,2000:1301–1306.[12]ARCAK M,SERON M,BRASLAVSKY J,et al.Robustification of backstepping against input unmodeled dynamics[J].IEEE Transactions on Automatic Control,2000,45(7):1358–1363. [13]ARCAK M,KOKOTOVIC P.Robust nonlinear control of systems with input unmodeled dynamics[J].Systems&Control Letters,2000,41(2):115–122.[14]HOU M Z,WU A G,DUAN G R.Robust output feedback control for a class of nonlinear systems with input unmodeled dynamics[J].International Journal ofAutomation&Computing,2008,5(3):307–312.[15]WANG Xingping,ZHANG Jinchun,CHENG Zhaolin.Output feedback robust stabilization for a class of nonlinear systems with input unmodeled dynamics[J].ControlTheory&Applications,2005,22(3):507–510.(王兴平,张金春,程兆林.一类带不确定输入动态非线性系统的输出反馈鲁棒镇定[J].控制理论与应用,2005,22(3):507–510.)[16]NUSSBAUM R D.Some remarks on a conjecture in parameter adaptivecontrol[J].Systems&Control Letters,1983,3(5):243–246.[17]YE X D.Adaptive nonlinear output-feedback control with unknown high-frequency gain sign[J].IEEE Transactions on Automatic Control,2001,46(1):112–115.[18]YE X D.Asymptotic regulation of time-varying uncertain nonlinear systems with unknown control directions[J].Automatica,1999,35(5):929–935.[19]GE S S,HONG F,LEE T H.Adaptive neural control of nonlinear time-delay system with unknown virtual control coefficients[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2004,34(1):499–516.[20]ZHANG T P,SHI X C,ZHU Q,et al.Adaptive neural tracking control of pure-feedback nonlinear systems with unknown gain signs and unmodeleddynamics[J].Neurocomputing,2013,121(2):290–297.[21]ZHANG Tianping,SHI Xiaocheng,SHEN Qikun,et al.Adaptive neural-network dynamic surface control with unmodeled dynamics[J].Control Theory&Applications,2013,30(4):475–481.(张天平,施枭铖,沈启坤,等.具有未建模动态的自适应神经网络动态面控制[J].控制理论与应用,2013,30(4):475–481.)[22]ZHANG Tianping,CHEN Jiasheng,XIA Xiaonan.Output feedback adaptive control of systems with input and state unmodeled dynamics[J].Control andDecision,2015,30(10):1847–1853.(张天平,陈佳胜,夏晓南.具有输入及状态未建模动态系统的输出反馈自适应控制[J].控制与决策,2015,30(10):1847–1853.)[23]XIA X N,ZHANG T P,ZHU J M,et al.Adaptive output feedback dynamic surface control of stochastic nonlinear systems with state and input unmodeled dynamics[J].International Journal od Adaptive Control and Signal Processing,2016,30(6):864–887.[24]SHI X C,ZHANG T P,ZHU Q.Robust adaptive control with unmodeled dynamics and unknown dead-zones[C]//Proccedings of 2013 Chinese Control and Decision Conference.New York:IEEE,2013:444–449.[25]JIANG Z P,PRALY L.Design of robust adaptive controllers for nonlinear systems with dynamic uncertainties[J].Automatica,1998,34(7):825–840.。

非匹配不确定非线性系统自适应模糊控制随着科学技术的进步,许多实际工程控制系统日趋复杂,往往呈现出严重的不确定性、非线性性、多变量性、强耦合性等特征,因此研究复杂不确定非线性系统的控制问题不仅具有重要的理论意义,而且具有广泛的应用价值。

自适应模糊控制是解决此类复杂系统控制设计问题的重要方法之一。

本文以模糊控制、自适应控制和非线性鲁棒控制为理论框架,用模糊逻辑系统对不确定非线性系统进行模糊建模,针对典型的不确定非线性系统,提出了一系列自适应模糊控制方法和策略,并应用数学方法给出了模糊闭环系统的稳定性、收敛性和鲁棒性的理论证明。

主要研究工作如下：1.针对三类状态可测的非匹配单输入单输出不确定非线性系统,分别提出自适应模糊状态反馈控制设计方法。

三类非线性系统分别包含未知的非线性函数、非光滑非线性输入(饱和输入、死区输入、滞回等)、未建模动态和随机扰动。

设计中,模糊逻辑系统分别用来辨识系统未知非线性函数或组合函数,基于反步递推设计方法、自适应鲁棒控制理论、随机小增益技术、障碍函数技术和自适应模糊控制技术,给出三种自适应模糊控制器设计方案,并基于李雅普诺夫稳定理论和随机稳定理论证明闭环系统的稳定性和收敛性。

仿真研究进一步验证所提方法的有效性。

2.针对三类状态不可测的非匹配单输入单输出不确定非线性系统,分别提出自适应模糊输出反馈控制设计方法。

三类非线性系统的状态均不可测,且系统包含未知的非线性函数、饱和输入、死区输入和未建模动态。

设计中,模糊逻辑系统用来辨识系统的未知非线性函数,分别设计模糊滤波观测器和模糊状态观测器估计系统的不可测状态,基于所设计的滤波观测器和状态观测器,并结合反步递推设计方法、自适应鲁棒控制理论、小增益技术、自适应模糊控制技术和动态面控制技术,给出三种自适应模糊输出反馈鲁棒控制器设计方案,并基于李雅普诺夫稳定理论证明闭环系统的稳定性和收敛性。

仿真研究进一步验证所提方法的有效性。

3.针对两类状态不可测的非匹配不确定非线性互联大系统,分别提出自适应模糊输出反馈分散控制设计方法。

不确定系统的自适应反步控制系统中的不确定性是指描述被控对象及其所处环境的数学模型是不完全确定的,其中可能包含某些未知因素或随机因素。

客观地说,任何一个实际系统都具有不同程度的不确定性。

它们可能表现在系统内部,也可能表现在系统外部。

系统内部的不确定性通常指的是描述被控对象的数学模型的结构和参数存在的不确定性,如未建模动态,未知系统参数和未知控制系数,设计者事先不能确切知道。

而系统外部的不确定性则可能来自于不可预知的执行器延迟或随机性的扰动等,例如时间大小不可预知的确定性的常值控制输入时延以及统计特性未知的随机性测量噪声等。

如果在进行控制设计的时候不充分考虑这些不确定性的影响,则被控对象的性能可能达不到所要求的效果,严重的甚至可能会导致系统不稳定。

面对这些客观存在的各式各样的不确定性,如何设计适当的控制律,使闭环系统稳定,并能实现某些期望的性能指标,是自适应控制所要研究解决的问题。

本论文的主要研究对象为不确定非线性时变系统、不确定线性最小相位系统、不确定线性时滞系统等多种类型的不确定对象,采用的主要控制手段是一种使用非常广泛的自适应反步控制方法(Adaptive Backstepping)。

因为被控对象的多样性,传统的自适应Backstepping方法无法实现所期望的控制目标,所以本论文针对不同的被控系统,对Backstepping方法进行了改进,也将这种方法与其它的控制方法进行了适当的结合,通过研究取得了以下的成果,(1)针对具有参数化严格反馈形式的带有跳变参数的非线性时变系统提出了一种基于模块的自适应反步控制方法。

这里考虑的未知参数既包括连续时变参数,也包括分段跳变参数,而且它们不必局限于缓慢时变或非频繁跳变,控制器模块和参数估计器模块这两个模块的设计是相互独立的。

稳定性分析显示整个闭环系统信号是全局一致有界的,关于参数变化速率的均方意义下的跟踪误差性能也得到了保证。

(2)针对不确定最小相位线性系统提出了一种新的基于输出反馈的自适应反步控制方法。

目录第一章自适应控制概述 (1)第一节自适应控制的产生背景及分类 (1)一.自适应控制产生的背景 (1)二.自适应控制的原理及分类 (2)第二章模型参考自适应控制（MODEL REFERENCE ADAPTIVE CONTROL）简称MRAC 3第一节MRAC的基本概念 (3)第二节最优化的设计方法 (4)一、利用梯度法的局部参数最优化的设计方法 (4)第三节基于李雅普诺夫第二方法稳定性理论的MRAC设计方法 (7)一．关于李雅普诺夫( Liaupunov) 稳定性的第二方法 (7)第四节基于超稳定理论的MRAC设计方法 (13)一、关于超稳定性理论的基本概念 (13)二、用超稳定理论设计MRAC系统 (15)第三章自校正控制 (18)第一节自校正控制的原理及组成 (18)第二节最小方差控制律 (21)第一章自适应控制概述任何一个动态系统，通常都具有程度不同的不确定性。

这种不确定性因素的产生主要由于：(1)系统的输入包含有随机扰动，如飞行器飞行过程中的阵风；(2) 系统的测量传感器具有测量噪声；以上两者又称为不确定性的（或随机的）环境因素。

(3) 系统数学模型的参数甚至结构具有不确定性。

如导弹控制系统中气动力参数随导弹飞行高度、速度、导弹质量及重心的变化而变化。

在只存在不确定环境因素，但系统模型具有确定性的情况下，这是随机控制需要解决的问题；而自适应控制是解决具有数学模型不确定性为特征的最优控制问题。

这时如果系统基本工作于确定环境下，则称为确定性自适应控制；如果系统工作于随机环境下，则称为随机自适应控制。

自适应控制的提法可归纳为：在系统数学模型不确定的条件下（工作环境可以是基本确定的或是随机的），要求设计控制规律，使给定的性能指标尽可能达到及保持最优。

为了完成以上任务，自适应控制必须首先要在工作过程中不断地在线辨识系统模型（结构及参数）或性能，作为形成及修正最优控制的依据，这就是所谓的自适应能力，它是自适应控制主要特点。

自适应控制算法的研究与应用自适应控制算法是一种根据被控对象时变特性而自适应改变控制策略的控制方法。

目前，自适应控制算法得到了广泛的研究和应用，已经成为现代控制工程中的一项重要技术。

本文将从自适应控制算法的定义、研究历史、算法原理、应用领域和未来展望等方面进行探讨。

一、自适应控制算法的定义自适应控制算法是一种针对动态、时变被控对象的自适应控制方法。

控制系统在运行过程中，根据被控对象的实际变化情况，通过自调整控制参数以及改变控制策略，以适应被控对象的时变特性，从而实现优化控制。

自适应控制算法的本质是通过自适应调整控制参数，对被控对象进行优化控制。

二、自适应控制算法的研究历史早在20世纪50年代，人们开始关注自适应控制算法的研究。

1950年，美国控制论专家艾伦·波里（Allen B. Poley）提出了自适应控制的基本思想。

60年代，由于控制对象日趋复杂，自适应控制算法开始得到更广泛的研究。

自适应控制算法的发展经历了几个重要阶段，如模型参考自适应控制、模型迭代控制、模型自适应控制、直接自适应控制等。

三、自适应控制算法的原理自适应控制算法的核心是通过对被控对象的状态进行实时监测和调整控制参数，实现对被控对象的实时适应。

自适应控制算法一般包含以下步骤：1、采集被控对象的状态信息自适应控制算法需要通过传感器等设备对被控对象的状态信息进行采集，例如温度、压力、速度、位置等。

2、建模和识别被控对象自适应控制算法需要通过数学模型对被控对象进行建模分析，以便识别被控对象的状态特性和变化规律。

3、选择控制策略自适应控制算法需要根据被控对象的实际状态，选择最优的控制策略，例如比例积分控制、模糊控制、神经网络控制等。

4、自适应调整控制参数自适应控制算法还需要通过自适应调整控制参数，从而实现对不同状态下被控对象的优化控制。

四、自适应控制算法的应用领域自适应控制算法已经广泛应用于机械、电子、化工、冶金、航空、航天等领域。