当前位置：文档之家 › 理论力学4 平面任意力系

理论力学4 平面任意力系

  • 格式：ppt
  • 大小：4.49 MB
  • 文档页数：42

下载文档原格式

  / 42

合集下载

理论力学L4-4 空间力系简化

理论力学L4-4 空间力系简化

c ) 一般主矢和主矩矢既不平行也不垂直 由共点矢量知，它们在同一平面内， 假设两矢量正向夹角为α。 ' FR 1) 将 M O分解为垂直于 ' ' ' 的 及平行于 F M R MO MO O " 的 MO ， ' ' O M O 的大小： " FR ' MO M O M O sin
' b) 若主矢平行于主矩：FR // M o
O
MO
' 由一个力和一个力偶(且力 FR 垂直于力偶作用面)组成的
力系，称为力螺旋。 力和力偶都是基本力学量， 力螺旋不能再简化。
力偶矩矢与力矢同方向的称为右螺旋(力偶的转 向与力的方向符合右手关系)；反之称左螺旋。 但一般主矢和主矩矢既不平行也不垂直。
§4-4 空间任意力系向一点简化
一、空间任意力系向一点简化 与平面任意力系向一点简化相似，空间任意力 系也是利用力的平移定理将各力平移到简化中 心 O 处，并附加矢量表示的空间力偶，则原力 系与空间汇交力系＋空间力偶系等效。
MO m m1 n
F2 F’2
F’R
O
F’n
Fn
F’1 m2
F 又由于力偶矩矢是自由矢量，再将平行于 的 R '' 力偶矩矢 M o 平行移动与FR 重合，成为力螺旋。 一般情况下，空间力系简化结果是一个力螺旋。
约束类型
约束反力
数量
空 间 约 束 类 型 和 约 束 反 力
3
4
5 6
MO
F’R
对于空间汇交力系的合 ' 力FR ：
O
' FR 等于该力系各力的矢量和， 称其为该力系的主矢； 对于空间力偶系的合力偶，其力偶矩矢 M O等于 各附加力偶矩的矢量和，也是力系中各力对点O 力矩矢的矢量和： MO mi mO ( Fi ) 称为该力系对简化中心O点的主矩。

理论力学2.2、平面任意力系的合成与平衡

理论力学2.2、平面任意力系的合成与平衡
m F1 OA F2 OB F1 ( OB OA) F1 AB
m F1 OA F2 OB F1 ( OA OB ) F1 AB
3
力 线 作用在刚体上的力可以离开其作用线而平 平 行移动到刚体上任意位置处,但必须对刚体 移 附加一个力偶,附加力偶的力偶矩等于原力 定 对平移后所得新力作用点的力矩。 理
求细绳的拉力和A、B两处的支持力。
解、研究对象：AB，受力 如图所示，则有：


Fix Fiy mD
0 0
(Fi )

0

FB FD G FA c
FA
os
sin 0
FB

BD

G

AB 2
0 sin
FA

AD

0
FA 115.5(N) FB 72.2(N ) FD 129.9(N) 12
例2.2-6、匀质细杆AB长度为L，重量为mg，静 止在半径为r的光滑半圆槽内（图2.2-17），
L=3r；求AB杆与水平线之间的夹角
解、研究对象:AB杆,受力如 图所示,则有:
Fix 0 Fiy 0 mO (Fi ) 0

FB FB
cos(2 ) FD sin sin(2 ) FD cos
d mO 2402 3.39(m) FR 709 .5
xE
d
sin

3.39 sin 70.8
3.59(m)
y yE tan 70.8 (x xE ) y 2.87x 10.31 0
10
课堂练习题(图示)：

平面任意力系的平衡条件和平衡方程

平面任意力系的平衡条件和平衡方程

理论力学 3-2平面任意力系的平衡条件和平衡方程 图 3-8 b
理论力学 3-2平面任意力系的平衡条件和平衡方程
（2）按图示坐标列平衡方程
理论力学 3-2平面任意力系的平衡条件和平衡方程
（3）解方程 解方程，求得
负号说明图中所设方向与实际情况相反，即 MA 为顺时针转向。
理论力学 3-2平面任意力系的平衡条件和平衡方程
二、关于平面任意力系 的例题
理论力学 3-2平面任意力系的平衡条件和平衡方程
例3-2 起重机 P1 = 10 kN，可绕铅直轴AB转动；
起重机的挂钩上挂一重为 P2 = 40 kN 的重物， 如图 3-6 所示。
起重机的重心C到转动轴的距离为1.5 m， 其他尺寸如图所示。
求在止推轴承 A 和轴承 B 处的约束力。
理论力学 3-2平面任意力系的平衡条件和平衡方程
b．如果力系对另一点 B的主矩也同时为 零，则这个力系或一合力沿 A，B 两点的连 线，或者平衡（图3-9）。
c．如果再加上
，那么力系如
有合力，则此合力必与 x 轴垂直。
理论力学 3-2平面任意力系的平衡条件和平衡方程 图 3-9
理论力学 3-2平面任意力系的平衡条件和平衡方程
理论力学 3-2平面任意力系的平衡条件和平衡方程
解： （1）选梁AB为研究对象 梁 AB 所受的主动力有： 均布载荷 q，
重力 P 和矩为 M 的力偶。 梁AB所受的约束力有： 铰链 A 的两个分力 Fax 和 FAy ，滚动支
座 B 处铅直向上的约束力FB。
理论力学 3-2平面任意力系的平衡条件和平衡方程
（2）列平衡方程 取坐标系如图3-7所示，列出平衡方程：
理论力学 3-2平面任意力系的平衡条件和平衡方程

理论力学第四章任意力系

理论力学第四章任意力系

OI x
点
Fi
Fi
一般力系（任意力系）向一点简化 汇交力系+力偶系
汇交力系 力偶系
合力 —— R'(主矢) ， (作用在简化中心)
合力偶矩——MO (主矩) ，(作用在该平面上)
O 点为简化中心: F1' F1 , F2 ' F2 ,, Fi ' Fi .
m1 MO (F1), m 2 MO (F2 ), , m i MO (Fi ).
tan1 FRx 70.83 0
FR
2）求主矩
y
O MO

MO 3F1 1.5P1 3.9P2 2355 kN m
x
FR '
y 3m
２）求合力与基线OA的交点到Ｏ点的距
▼
9m
F1
3m
P1
1.5
P2
3.9 m
离 x及合力作用线方程
▼
主矩：MO 3F1 1.5P1 3.9P2
y
3m
▼
P1
1.5
解:１）求 FR'x , FR'y
FR'x F1 F2 cos 300 70 cos16.7
232.9kN
▼
FR'y P1 P2 F2 sin
9m
F1
P2 F2 450 200 70sin16.7 670.1kN
3.9 m 3m
MO2

M O1 FR
FR
M O1
FR
o d O
o d O
MO1 是自由矢量，可搬到O'处
所以在O'点处形成一个力螺旋。

第四章、平面任意力系

第四章、平面任意力系

分布力系说明
q
qB
A
L 2L/3 Q1 L/3
B
A L L/2 A Q L/2
B
A
L (a)三角形分布力
厚接分布力
B L （b）均匀分布力
在以后碰到分布力时，先进行简化处理，然后再求解。
第四章 平面任意力系
理 论 力 学
§4- 4 平衡条件、平衡方程
例 4-1
已知：梁AD的支承及受力如图所示。
F = 500N, FA = 1000N, q = 1000N/m
A、B、C是平面内不共线的任意三点.
应当指出：投影轴和矩心是可以任意选取的。 在解决实际问题时适当选取矩心与投影轴可以简化计算。
一般地说，矩心应选多个力的交点，尤其是选
未知力的交点，投影轴则尽可能选取与该力系中多数力的 后接例题 作用线平行或垂直。
第四章 平面任意力系
理 论 力 学
§4- 5 平面平行力系的合成与平衡
即两个力矩式一个投影式，其中A、B是平面内任意两点。 但连线不能垂直投影轴 X 。 B A x
第四章 平面任意力系
理 论 力 学
§4- 4 平衡条件、平衡方程
平衡方程
2、平面力系任意力系的平衡方程 B
A 即三个力矩式， C
（2）三力矩形式的平衡方程
∑MA （F）= 0，
∑MB （F）= 0 ∑MC （F）= 0
即距D点的距离为a/3。
应用平面力系平衡方程求解。
第四章 平面任意力系
理 论 力 学
§4- 4 平衡条件、平衡方程
例 4-1 ∑Fx = 0 ∑Fy= 0
步骤3：取坐标系Bxy，列平衡方程
FBx+ F = 0 FBy+ FC- Fp- FA= 0

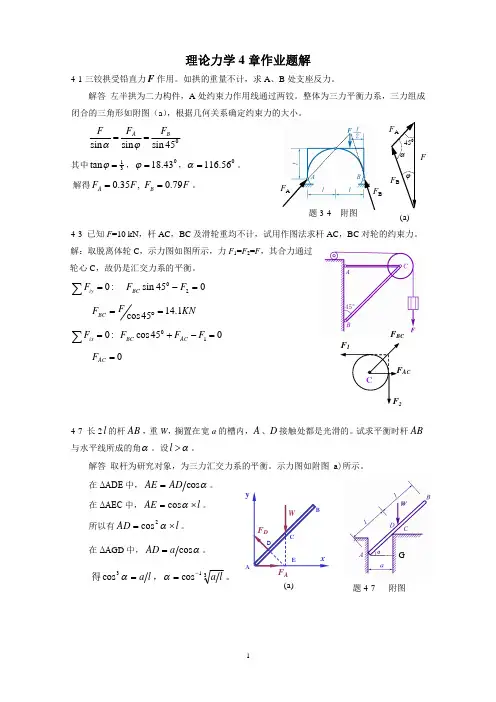
《理论力学》第四章-力系平衡试题及答案

《理论力学》第四章-力系平衡试题及答案

理论力学4章作业题解4-1三铰拱受铅直力F 作用。

如拱的重量不计，求A 、B 处支座反力。

解答 左半拱为二力构件，A 处约束力作用线通过两铰。

整体为三力平衡力系，三力组成闭合的三角形如附图（a ），根据几何关系确定约束力的大小。

45sin sin sin B A F F F ==j a其中31tan =j ，043.18=j ，056.116=a 。

解得F F F F B A 79.0 ,35.0==。

4-3 已知F =10 kN ，杆AC ，BC 及滑轮重均不计，试用作图法求杆AC ，BC 对轮的约束力。

解：取脱离体轮C ，示力图如图所示，力F 1=F 2=F ，其合力通过轮心C ，故仍是汇交力系的平衡。

:0=åiyF 045sin 20=-F F BCKN FF BC 1.1445cos =°=045cos :010=-+=åF F F FAC BC ix0=AC F4-7 长2l 的杆AB ，重W ，搁置在宽a 的槽内，A 、D 接触处都是光滑的。

试求平衡时杆AB 与水平线所成的角a 。

设a >l 。

解答 取杆为研究对象，为三力汇交力系的平衡。

示力图如附图(a)所示。

在ΔADE 中，a cos AD AE =。

在ΔAEC 中，l AE ´=a cos 。

所以有l AD ´=a 2cos 。

在ΔA GD 中，a cos a AD =。

得a =a 3cos ，31cosl a -=a 。

F BCAC题3-4 附图F BF AF BF AFa45j(a)A (a)题4-7 附图G4-9 AB ，AC ，AD 三连杆支撑一重物，如图所示。

已知W=10kN ，AB =4m ，AC =3 m ，且ABEC 在同一水平面内，试求三连杆所受的力。

解：取铰A 研究，示力图如图示，为汇交力系的平衡。

0=åix F ： 05430sin =´°+AD AB F F 0=åiy F ： 05330sin =´°+AD AC F F 0=åiZF： 030cos =-°W F AD联立求解KNF KNF KN F AD AC AB 5.115.36.4=-=-=4-8 图示结构上作用一水平力F 。

理论力学平面力系的简化和平衡

理论力学平面力系的简化和平衡

原力偶系的合力偶矩
n
M Mi i 1
只受平面力偶系作用的刚体平衡充要条件：
n
M Mi 0 i 1
对BC物块对B点取矩，以逆时针为正列方程应为：
M 2 M B (FC ) M FCY a FCx b M FC (b a) cos45 0
[例] 在一钻床上水平放置工件,在工件上同时钻四个等直径 的孔,每个钻头的力偶矩为 m1m2 m3 m4 15Nm 求工件的总切削力偶矩和A 、B端水平反力?
两轴不平行即 条件：x 轴不 AB
可，矩心任意
连线
mA (Fi ) 0 mB (Fi ) 0 mC (Fi ) 0
③三矩式 条件：A,B,C不在
同一直线上
上式有三个独立方程，只能求出三个未知数。
4. 平面一般力系的简化结果分析
简化结果： 主矢R ，主矩 MO ，下面分别讨论。 ① R =0， MO =0，则力系平衡,下节专门讨论。 ② R =0,MO≠0 即简化结果为一合力偶, MO=M 此时刚
解除约束，可把支反
力直接画在整体结构
的原图上）
解除约束
由
mA (Fi
)
0
P2a N B
3a0,
N B
2P 3
X 0 XA 0
Y 0 YB NB P0,
YA
P 3
2.5物体系统的平衡、静定与超静定问题
1、物体系统的平衡问题 物体系统（物系）：由若干个物体通过约束所组成的系统叫∼。 [例]
外力：外界物体作用于系统上的力叫外力。 内力：系统内部各物体之间的相互作用力叫内力。
N2个物体受平面汇交力系（或平面平行力系）
X 0 Y 0
2*n2个独立平衡方程
N3个物体受平 X 0 面任意力系 Y 0

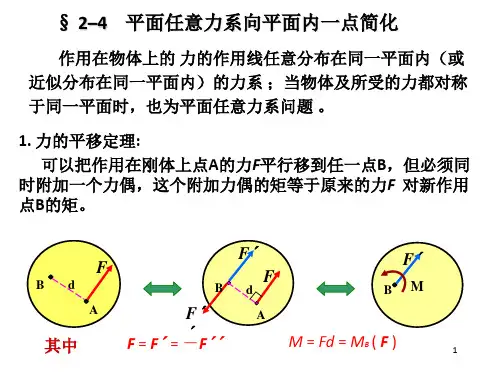
理论力学第2章平面任意力系

理论力学第2章平面任意力系

空载时轨道A 、 B的约束反力，并问此起重机在使用过程中有无翻
倒的危险。
解：
（1）起重机受力图如图
（2）列平衡方程 ：
MA 0:
Q
Q(6 2) RB 4 W 2 P(12 2) 0
MB 0:
Q(6 2) W 2 P(12 2) RA 4 0
6m
解方程得:
W
P
12m
RA 170 2.5P
FR' Fi Fxi Fy j
MO MO (Fi )
3. 平面任意力系的简化结果
（1）FR´= 0，Mo ≠ 0, （2）FR´ ≠ 0，Mo = 0, （3）FR´≠ 0，Mo ≠ 0, （4）FR´= 0，Mo = 0,
合力偶，合力偶矩，MO MO (Fi )
合力，合力作用线通过简化中心O。
3
F2
j
F3
x
(437.6)2 (161.6)2
F1
1 1
100
Oi
1 2
466.5N
200
MO 21.44N m
y
合力及其与原点O的距离如图(c) 。 MO
x
y
d
x
O
FR FR′ 466.5N FR´
FR
O
d MO 45.96mm
(b)
(c)
FR
10
例11 水平梁AB受按三角形分布的载荷作用，如图示。载荷的
M
l
l
30
B
D
° F
3l
P
q
A
21
解：T字形刚架ABD的受力如图所示。
M
l
l
Fx 0
30
B
FAx 1 • q • 3a Fcos30 0

理论力学平面任意力系_1简化与平衡

理论力学平面任意力系_1简化与平衡
第四章
平面任意力系
平面任意力系： 力系中各力的作用线在同一平面内任意分布
本章讨论平面任意力系的简化（合成）与平衡问题
第一节 平面任意力系向一点的简化
一、力的平移定理 作用于刚体上的力可等效地平移至任一指定点，但必须附加一力 偶，附加力偶的矩就等于原力对指定点的矩
F
F
B d
A
F
B d
F
B
说明： 1）可解 2 个未知量
2）矩心位置可任意选择
[例2] 如图，悬臂梁 AB 上作用有矩为 M 的力偶和集度为 q 的均 布载荷，在梁的自由端还受一集中力 F 的作用，梁长为 l ，试求 固定端 A 处的约束力。
q
A
M
F
FAx
B
q
A
M
F
a
l
MA
B
FAy
解： 1）选取梁 AB 为研究对象 2）受力分析
2. （一投影两矩式 ）
F 0 M F 0 M F 0
ix
A
i
B
i
其中，A、B 两点连线不垂直于 x 轴
3. （三矩式）
M F 0 M F 0 M F 0
A i B i C i
所受的力大小为 0.85 kN，是拉力。
[例5] 横梁 AB 用三根杆支撑，受图示载荷。已知 F = 10 kN， M = 50 kN· m，若不计构件自重，试求三杆 所受的力。
F
2m 3m
30
2m
3m
30
F
M
B
A
1
45
B
A
45
2
3
M

理论力学第4章-平面任意力系

理论力学第4章-平面任意力系

FAx
FAy MA
解：（1）取悬臂刚架为研究对象，受力图。
（2）列平衡方程
Fx 0
FAx F 0
Fy 0
FAy 3q 0
解之得
MA(F) 0
M A F 4 3q 1.5 0
FAx 5kN FAy 6kN M A 11 kN m（与假设相反）
4.5.2 平面平行力系的平衡方程 作用线分布在同一平面内且相互平行的力系，称为平 面平行力系。
MO (F ) 2 OAB面积
（1）当力F通过矩心O时，力对该矩心的力矩为零。 （2）当力F沿作用线移动时，不改变该力对任一点的矩。
力对点之矩的解析式：
MO (F ) Fd Fr sin( ) Fr sin cos Fr cos sin
Fr cos Fx
r cos x
Fr sin Fy
合力矢 作用线的方程。
MO FRx
O
38.66
F Ry
F R
（x, y） FRx
400 x + 500 y = 2726.7
O
FRy
FR
4.5 平面任意力系、平面平行力系平衡方程 4.5.1 平面任意力系的平衡方程 平面任意力系平衡的必要与充分条件为：力系的
主矢以及对作用面内任一点的主矩都等于零，即
r sin y
MO (F ) xFy yFx （4-4）
y
Fy
F
y
r O d
A Fx
x
x
4.2 力线平移定理
力线平移定理： 作用在刚体上A点的力F可以平行 移到任一点B，但必须同时附加一个力偶，此附加力 偶的矩等于原来的力F对B点的矩。
[证] 力 F
力系 F, F1, F1' 力F1 力偶（F, F1'）

理论力学作业参考答案

理论力学作业参考答案

平面任意力系(一)一、填空题1、平面任意力系的主矢RF '与简化中心的位置 无 关,主矩o M 一般与简化中心的位置 有 关,而在__主矢为零___的特殊情况下,主矩与简化中心的位置 无 __ 关.2、当平面力系的主矢等于零，主矩不等于零时，此力系合成为_一个合力偶.3、如右图所示平面任意力系中,F F F F 1234===,此力系向A 点简化的结果是 0R F '≠,0A M ≠ ,此力系向B 点简化的结果是0RF '≠,0A M = . 4、如图所示x 轴与y 轴夹角为α，设一力系在oxy 平面内对y 轴和x轴上的A ，B 点有∑A m 0)(=F ,∑B m 0)(=F ,且∑=0y F ,但∑≠0x F ,l OA =,则B 点在x 轴上的位置OB =___/cos l θ ____.（题4图） （题5图）5、折杆ABC 与CD 直杆在C 处铰接,CD 杆上受一力偶m N 2⋅=M 作用,m 1=l ,不计各杆自重,则A 处的约束反力为___2N___. 二、判断题(√ ) 1.若一平面力系对某点之主矩为零,且主矢亦为零，则该力系为一平衡力系.(√ ) 2.在平面力系中，合力一定等于主矢.(× ) 3.在平面力系中，只要主矩不为零，力系一定能够进一步简化.1F 2F 3F 4F AB(√ ) 4.当平面任意力系向某点简化结果为力偶时,如果再向另一点简化,则其结果是一样的.(×) 5.平面任意力系的平衡方程形式,除一矩式,二矩式,三矩式外,还可用三个投影式表示.(× ) 6.平面任意力系平衡的充要条件为力系的合力等于零.(× ) 7.设一平面任意力系向某一点简化得一合力,如另选适当的点为简化中心,则力系可简化为一力偶.(√ ) 8.作用于刚体的平面任意力系主矢是个自由矢量,而该力系的合力(若有合力)是滑动矢量,但这两个矢量等值,同向.( × ) 9.图示二结构受力等效.三、选择题1、关于平面力系与其平衡方程式，下列的表述正确的是_____D_ ___A.任何平面任意力系都具有三个独立的平衡方程。

理论力学平面任意力系

理论力学平面任意力系
齿轮II上旳力偶矩M；轴 承A，B处旳约束力。
解: 取齿轮I及重物C ,画受力图.
M B 0 Pr F R 0 F 10 P1
由 Fr taan 200 3.64 P1
t
X 0 FBx Fr 0 FBx 3,64P1
Y 0 FBy P P2 F 0 FBy 32P1
[例1]
静定（未知数三个）
静不定（未知数四个）
[例2]
物体系统（物系）： ——由若干个物体经过 约束所构成旳系统。
超静定拱
[P62 思索题 3-10]
超静定梁
超静定桁架
3-3 物体系旳平衡•静定与超静定问题
二、物体系统旳平衡问题
外力：外界物体作用于系统上旳力。 内力：系统内部各物体之间旳相互作用力。
R
主矢
FR 0 FR 0
主矩
MO 0
MO 0 MO 0
MO 0
最终成果
阐明
合力 合力作用线过简化中心
合力 合力偶
合力作用线距简化中心M O FR
与简化中心旳位置无关
平衡
与简化中心旳位置无关
3-2 平面任意力系旳平衡条件与平衡方程
一、平面任意力系平衡旳充要条件为：
力系旳主矢
FR
'和对于任一点旳主矩
独立方程旳数目
平面力偶系
mi 0
1
平面平行力系 Y 0, mo (F ) 0
2
平面汇交力系
X 0
2
Y 0
平面任意力系
X 0
Y
0
3
mO (F i ) 0
3-3 物体系旳平衡•静定与超静定问题
独立方程数目≥未知数数目时，是静定问题 （可求解） 独立方程数目<未知数数目时，是超静定问题（静不定问题）

材料力学第4章 平面任意力系

材料力学第4章 平面任意力系

MO

M1

M
2

M
n

(2-2)
MO (F1) MO (F2 ) MO (Fn ) MO (F )
由此可见，MO一般与简化中心的位置有关，它
反映了原力系中各力的作用线相对于点O的分布情
况，称为原力系对点O的主矩。
理论力学
静力学
平面任意力系
15
平面任意力系向作用面内任意一点简化，一般 可以得到一个力和一个力偶；该力作用于简化中心， 其大小及方向等于力系的主矢，该力偶之矩等于力 系对于简化中心的主矩。
(2)
理论力学
静力学
平面任意力系
37
例题

MA(F) 0
FT AB sin 300 P AD F AE 0
(3)
由(3)解得
FT

2P 3F 4sin 300

(2 4 3 10)kN m 4m 0.5

19
kN
以
FT
之值代入式(1)、
例如，铁轨给轮 子的力等。
理论力学
静力学
平面任意力系
28
几种分布荷载：
体分布荷载：荷载（力）分布在整个构件内部
各点上。例如，构件的自重等。 面分布荷载：分布在构件表面上。例如，风压
力、雪压力等。
线分布荷载：荷载分布在狭长范围内，如沿构
件的轴线分布。
理论力学
静力学
平面任意力系
29
荷载的单位
(1) 集中荷载的单位，即力的单位 (N，kN)。 分布荷载的大小用集度表示，指密集程度。
值为多少？
理论力学
静力学

郭新柱 理论力学(第三章)

郭新柱 理论力学(第三章)
即平面力系向点 B 简化得到一力和一力偶，该力过点 B ，其大小和方向与力系的主矢 F 相
同。该力偶的力偶矩等于主矩 M B ，如图 b
y
y
MC
A B
F
3、向 C 点简化的主矩
D C
x
F
A (-3,0) B
D Cx
利用两点之矩的关系计算 M C M B M C F 3 Fy 2 5KN
o 1 1 2
（2）、求合力及其作用线位置。
Mo 2355 d 3.3197m ' FR 709.4
d x 3.514m 0 0 cos 90 70.84
（3）、求合力作用线方程
' ' M o M o FR x FRy y FRx x FRy y FRx
FR 0 FR 0
MO 0 MO 0 MO 0 MO 0
FR
与简化中心的位置无关
与简化中心的位置无关
简化
FR
简化 中心
①
=0， MO =0，则力系平衡,下节专门讨论。 FR
简化
M=MO
简化 中心
=0 FR
② FR =0,MO≠0 即简化结果为一合力偶, M=MO 此时刚体等效于只有一个力 偶的作用，因为力偶可以在刚体平面内任意移动，故这时， 主矩与简化中心O无关。
2 2
Fx 2 2 5 cos F 5 5
F 的解析式
5 cos F 5 5
Fy
1
F 2i 1 j
y
A
Fx MB Fy
D B Cx
2 向 B 点简化的主矩
F

理论力学4 平面一般力系

理论力学4 平面一般力系

力F ′+ 力偶（ F ， F ′′）
3
说明： 说明 力线平移定理揭示了力与力偶的关系： ①力线平移定理揭示了力与力偶的关系：力 （例断丝锥） 例断丝锥）
力+力偶 力偶
有关， ②力平移的条件是附加一个力偶m，且m与d有关，m=F•d 力平移的条件是附加一个力偶 ， 与 有关 ③力线平移定理是力系简化的理论基础。 力线平移定理是力系简化的理论基础。
Fx = 0, FAx − FT cos 30 0 = 0 ∑
Fy = 0, FAy + FT sin300 − P −Q = 0 ∑
1 ∑ M A = 0, FT 2 ⋅ 6a − P ⋅ 3a − Q ⋅ 4a = 0 F T = 17 . 33 kN 解得： F Ax = 15 . 01 kN 解得： F 22 Ay = 5 . 33 kN
a a 两力作用线过x1 = 和x2 = 3 2
17
§3-4
平面一般力系的平衡条件与平衡方程
一 平面任意力系的平衡方程 平面任意力系平衡的充要条件是： 力系的主矢和对任意点的主矩都等于零
r ′ 即 FR = 0
Mo = 0
FR′ = (∑ Fx )2 + (∑ Fy )2
MO = ∑MO (Fi )
∑ F = 0, F = 0 ∑ Fy = 0, FAy + FBy − P − q ⋅ 2a = 0
9
固定端（插入端） 固定端（插入端）约束 说明 ① 认为Fi这群力在同一平面内; 雨搭 ② 将Fi向A点简化得一力和一力偶; ③ FA方向不定可用正交分力FAX, FAY 表示; ④ FAX, FAY, MA为固定端约束反力;
FR FYA FXA

理论力学-平面任意力系

理论力学-平面任意力系

平面任意力系可能由 多个力的叠加构成， 具有较高的复杂性。
平面任意力系的特点
多方向性
平面任意力系可以有从不同方向作用的力。
多点作用性
平面任意力系可以有多个作用点。
力的大小不同
平面任意力系中的力可以有不同的大小。
力的叠加
平面任意力系可能由多个力的叠加构成。
平面任意力系的合力和力矩求解方法
1
合力求解方法
Hale Waihona Puke 理论力学-平面任意力系通过本讲，你将深入了解平面任意力系的定义、特点、合力和力矩求解方法、 平衡条件、实际应用，以及解题步骤。准备好开始你的力学之旅吧！
平面任意力系的定义
1 什么是平面任意
力系？
平面任意力系是指位 于同一平面内的多个 力的集合。
2 力的方向和作用点 3 任意力系的复杂性
力可以有不同的方向 和不同的作用点，但 都在同一平面内。
将所有力按照矢量法则相加，求
力矩求解方法
2
得合力的大小和方向。
通过力矩定理，求得平面任意力
系的力矩。
3
力矩的方向
力矩的方向垂直于力的平面。
平面任意力系的平衡条件
力的平衡
合力为零，即所有力合成为零。
力矩的平衡
力矩的合力为零。
平面任意力系的实际应用
1 桥梁结构分析
分析桥梁结构的受力 情况。
2 机械设计
设计和优化机械系统 中的力的分布。
3 建筑结构设计
分析建筑结构的静力 平衡。
案例分析：平面任意力系的解题步骤
1
Step 1
分析力的大小和方向。
2
Step 2
计算合力和合力矩。
3
Step 3
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4.4.3 两种常见线分布载荷 在工程上，常把作用于结构上的主动力称为载荷。 载荷除点接触的集中力载荷外，还有以体分布及线、 面接触形式出现的分布载荷。如重力（体分布载荷）、 水压力（面分布载荷、工程上也常简化为线分布载 荷），土压力、风压力等。 单位体积、面积、长度上所承受的力称载荷集度。 体载荷集度的单位为N / m3，面载荷集度的单位为N / m2，线载荷集度的单位为N / m。
F1 F2 F F FRy
a
F 2 cos(FR , i ) 2F 2
再计算主矩
FR 2 F
F FR
45o MO A F B （ F2 a ） x
(FR , i ) 45
h F3
O
F F1 a a
M O Fa F1 0 2F2 a F3h F ( a h)
A
FAx MA
MA
固定端约束对物体的作用，是在接触面上作用的 一群复杂的约束力。 固定端约束的约束反力表示为限制水平方向位移 的反力FAx和限制竖向位移的反力FAy，以及限制物体转 动的力偶矩为MA的反力偶。
4.4 平面任意力系的简化结果、合力矩定理
4.4.1 平面任意力系的简化结果分析 (1) FR 0 MO 0 平衡,（下节讨论）。
(2) 向A点简化：由于主矢 与简化中心的位置无关，所以
h F3
y O
F A F
FR
45o MA F x
FR 2 F
主矩
(FR , i ) 45
F1 a a
B （ F2 a ）
M A Fa F2a F3h Fh
(3) 向B点简化： 主矢
h F3
y O
F A F MB F a a B （ F2 a ） x
F FR = FR
简化中心O到合力矢 作用线的垂直距离d为
MO d FR
4.4.2 合力矩定理
因为 (合力偶) M O M O (F ) (主矩)
M O (FR ) FR d M O
所以
(合力偶)
M O (FR ) M O (F )
即：平面任意力系的合力对作用面内任一点之矩等 于力系中各力对于同一点之矩的代数和。
FR
45o
FR 2 F
主矩
(FR , i ) 45
F1
M B Fa 2F1a Fa
固定端约束的约束反力
物体的一部分固嵌于另一物体中所构成的约束称 为固定端约束 。 固定端约束的受力特点是：它限制了被约束的物 体既不能沿某一方向移动，又不能绕某一点转动。
F A A
A
FAy
(2) 主矩：指原平面一般力系对简化中心之矩的代数和
M O M1 M 2 M n M O ( F1 ) M O ( F2 ) M O ( Fn ) M O ( F )
主矢与简化中心位置无关， 主矩与简化中心的位置有关。 主矢的大小和方向余弦
F1 y Fny Fy FRy 2 2 ( Fx ) ( Fy ) FR FRy FRx , i) , j) cos( FR cos( FR FR FR F1x Fnx Fx FRx
[证 ] 力 F
A
力系 F , F1 , F1'
F
A B
力F1 力偶（F , F1' ）
A
F F1
d B
F1
B
M=MO ( F )
M Fd MO (F )
4.3 平面任意力系向一点的简化
y F1 O A2 An F A1 F Fn F y F2
F2
M2 O F Mn
F1
M1 F x O
M O (F ) 2 OAB面积
（1）当力F通过矩心O时，力对该矩心的力矩为零。 （2）当力F沿作用线移动时，不改变该力对任一点的矩。 力对点之矩的解析式： MO (F ) Fd Fr sin( ) Fr sin cos Fr cos sin
y
Fr cos Fx
Fr sin Fy
r sin y
y r O d
Fy A
F
r cos x

Fx
MO (F ) xFy yFx
（4-4）

x

x
4.2 力线平移定理 力线平移定理： 作用在刚体上A点的力F可以平行 移到任一点B，但必须同时附加一个力偶，此附加力 偶的矩等于原来的力F对B点的矩。
FR
MO F x
Fn
O—简化中心
M1 MO (F1 ) M 2
F1 F1 F2 F2
… Fn Fn M (F ) … M n MO (Fn )
Байду номын сангаасO 2
(1) 主矢：指原平面一般力系各力的矢量和 。
F1 F2 Fn F1 F2 Fn F FR
(2) FR 0 MO 0 合力偶 简化结果与简化中心O无关 (3) FR 0 MO 0
合力
简化结果与简化中心有关
(4) FR 0 MO 0 为最一般的情况。此种情况 还可以继续化为一个合力。
MO F O
FR
FR FR
O d O1
FR
O d O1
FR
O1
合力矢 等于原力系的主矢。
(1) 均布线载荷。 均布线载荷的合力大小
4 平面任意力 系
4.1 力对点之矩 力对刚体的作用使刚体产生两种运动效应，即移 动效应和转动效应。力对刚体的转动效应则用力对点 A 的矩来度量。 F对O点之矩，记为， MO (F )
O
F
B
（a）
MO (F ) Fd
d
O——力矩中心（Center of moment），简称矩心。 d——力臂 力矩是一个代数量，规定：逆时针取正号。 单位 ——牛· 米（N· m）或千牛· 米（kN· m）。
式中的i、j分别为沿x、y轴正向的单位矢量。
例4-1 如图所示刚体上作用平面力系F，F1，F2，F3，且F = F1 = F2 = F3。试求该力系向O点；A点；B点简化的主矢和主矩。 F 解：(1) 向O点简化：先计 算主矢。
A h F3 F1 a
y
F B （ F2 a ）
F3 F FRx