投影法和三视图基础
- 格式:pptx
- 大小:2.32 MB
- 文档页数:13

幻灯片1第二章投影基础第一节正投影及三视图一、正投影法(一)投影的概念在日常生活中,人们可以看到,当太阳或灯光照射物体时,墙壁上或地面上会出现物体的影子,这就是投影现象。
投影法是将这一现象加以科学总结而产生的。
投射线通过空间物体,向选定的面投射,并在该面上得到图形的方法称为投影法。
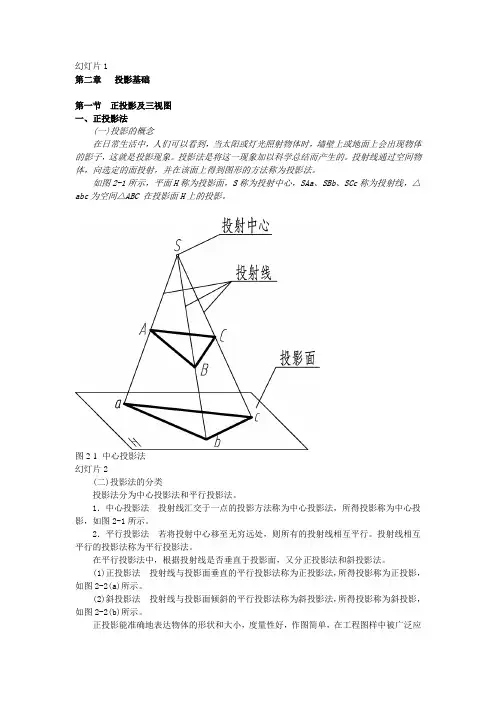
如图2-1所示,平面H称为投影面,S称为投射中心,SAa、SBb、SCc称为投射线,△abc为空间△ABC 在投影面H上的投影。
图2-1 中心投影法幻灯片2(二)投影法的分类投影法分为中心投影法和平行投影法。
1.中心投影法投射线汇交于一点的投影方法称为中心投影法,所得投影称为中心投影,如图2-1所示。
2.平行投影法若将投射中心移至无穷远处,则所有的投射线相互平行。
投射线相互平行的投影法称为平行投影法。
在平行投影法中,根据投射线是否垂直于投影面,又分正投影法和斜投影法。
(1)正投影法投射线与投影面垂直的平行投影法称为正投影法,所得投影称为正投影,如图2-2(a)所示。
(2)斜投影法投射线与投影面倾斜的平行投影法称为斜投影法,所得投影称为斜投影,如图2-2(b)所示。
正投影能准确地表达物体的形状和大小,度量性好,作图简单,在工程图样中被广泛应用。
本课程的后续章节中,除有特别说明外,提到的“投影”均指“正投影”。
幻灯片3图2-2 平行投影法幻灯片4(三)正投影的基本特性分析直线段和平面图形的正投影,如图2-3,可得出如下性质。
1.真实性当直线段或平面图形平行于投影面时,其投影反映实长或实形。
2. 积聚性当直线段或平面图形垂直于投影面时,其投影积聚成为一点或一直线。
3.类似性当直线段或平面图形倾斜于投影面时,直线段的投影比实长缩短,平面的投影面积缩小,形状与原平面图形类似。
图2-3 正投影的基本特性幻灯片5二、形体的三视图空间形体具有长、宽、高三个方向的形状,而形体相对投影面正放时得到的单面正投影图只能反映形体两个方向的形状。


初中数学知识归纳三视的法与投影关系数学中,三视图是指通过不同的视角观察一个物体所得到的三幅图像,分别展示了物体的正视图、侧视图和俯视图。
这种绘制方法可以帮助我们更好地理解物体的形状和结构。
在三视图的基础上,还有一个重要的概念,那就是投影关系。
在本文中,我们将对初中数学中的三视图法与投影关系进行归纳和总结。
一、三视图法的基本原理三视图法是通过使用直角投影的原理将一个物体从不同方向投影到不同的平面上,再将这些投影图形展示出来,从而形成一个全面的物体图形信息。
具体来说,三视图法包括以下几个基本原理:1. 正视图:以物体正面为观察面,将物体投影在水平面上得到的视图称为正视图。
正视图一般用物体的封闭轮廓线表示,如长方体的正视图是一个矩形。
2. 侧视图:以物体左侧或右侧为观察面,将物体投影在垂直平面上得到的视图称为侧视图。
侧视图能够展示物体的高度和深度,如长方体的侧视图是一个矩形。
3. 俯视图:以物体顶部为观察面,将物体投影在水平平面上得到的视图称为俯视图。
俯视图能够展示物体的长宽比例关系,如长方体的俯视图是一个矩形。
通过正视图、侧视图和俯视图的综合运用,我们可以绘制出一个物体的全貌,并且能够对物体的形状、尺寸和比例关系进行准确描述。
二、三视图法的实际应用三视图法在日常生活中有着广泛的应用,尤其是在工程设计、建筑设计和制造过程中起到了重要的作用。
下面通过一些例子来说明三视图法的实际应用。
1. 建筑设计:在建筑设计中,三视图法可以帮助建筑师将设计图纸清楚地呈现给施工方。
以一栋房子为例,正视图展示建筑的正面轮廓、门窗的位置等信息,侧视图展示建筑的高度和深度,俯视图展示建筑的布局和屋顶形状。
2. 机械制造:在机械制造中,三视图法可以帮助工程师将设计的零件准确传达给加工人员。
通过正视图、侧视图和俯视图,可以清晰地展示零件的各个面以及它们之间的相对位置关系,从而提高生产效率和准确性。
3. 衣物设计:在衣物设计中,三视图法可以帮助设计师将设计的服装展示给制作厂家。

2-1 投影法与三视图物体在光线照射下,在地面或墙壁上产生影子。
人们对这种自然现象加以抽象研究,总结其中规律,创造了投影法。
所谓投影法,就是投射线通过物体,向选定的平面(投影面)投影,并在该平面上得到图形(投影图)的方法。
投影法分为两大类:中心投影法和平行投影法。
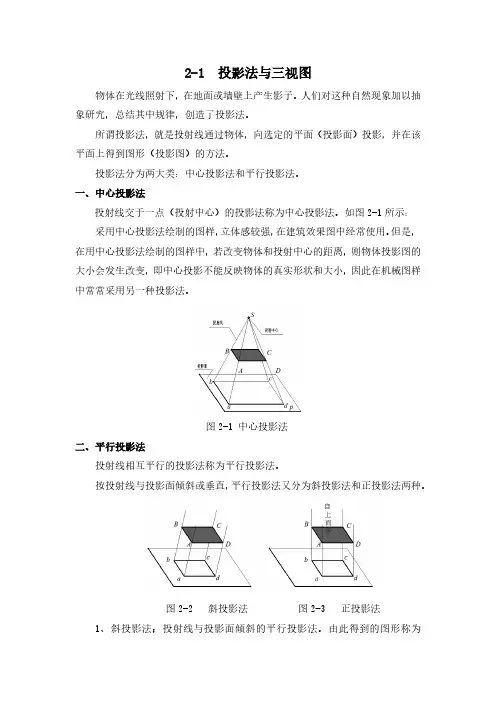
一、中心投影法投射线交于一点(投射中心)的投影法称为中心投影法。
如图2-1所示:采用中心投影法绘制的图样,立体感较强,在建筑效果图中经常使用。
但是,在用中心投影法绘制的图样中,若改变物体和投射中心的距离,则物体投影图的大小会发生改变,即中心投影不能反映物体的真实形状和大小,因此在机械图样中常常采用另一种投影法。
图2-1 中心投影法二、平行投影法投射线相互平行的投影法称为平行投影法。
按投射线与投影面倾斜或垂直,平行投影法又分为斜投影法和正投影法两种。
图2-2 斜投影法图2-3 正投影法1、斜投影法:投射线与投影面倾斜的平行投影法。
由此得到的图形称为斜投影图(简称斜投影)。
如图2-2所示。
2、正投影法:投射线与投影面垂直的平行投影法。
由此得到的图形称为正投影图(简称正投影)。
如图2-3所示。
正投影图度量性好,作图简单,机械图样常常采用正投影法绘制。
三、正投影的基本特性(单投影面)1、真实性:当物体上的平面(或直线)与投影面平行时,其投影反映实形(或实长)。
如图2-4(a)。
2、积聚性:当物体上的平面(或直线)与投影面垂直时,其投影积聚成直线(或点)。
如图2-4(b)。
3、类似性(亦称收缩性):当物体上的平面(或直线)与投影面倾斜时,其投影收缩成原来形状的类似形。
如图2-4(c)。
图2-4 正投影的特性四、三视图的形成及投影规律1、三投影面体系一般情况下,物体的一个投影图(二维)不能准确地反映物体(三维)的完整形状,如图2-5所示。
要想准确表达物体的结构形状,就必须增加投影图。
工程上常采用在三投影面体系中得到的三面投影图来表达物体的形状,如图2-6所示。


三视与投影的基本概念知识点总结三维视图和投影是工程制图中非常重要的概念,它们可以帮助我们更准确地理解和表达三维物体。
本文将对三视与投影的基本概念进行总结,并介绍相关的知识点。
1. 三视图三视图是用于展示物体在三个不同平面上的投影的图形,包括主视图、俯视图和侧视图。
主视图是物体在正交投影下的正面视图,俯视图是物体在正交投影下的俯视图,侧视图是物体在正交投影下的侧面视图。
通过同时观察三个视图,我们可以全面了解物体的形状和尺寸。
2. 投影投影是将三维物体映射到二维平面上的过程。
常见的投影方法有平行投影和透视投影。
平行投影是物体上各点到投影平面的投影线都是平行的,透视投影则根据透视规律进行投影,使得离观察者较近的物体较大,离观察者较远的物体较小。
在绘制三视图时,我们通常使用平行投影。
3. 正投影和斜投影根据投影线与投影平面的关系,投影可以分为正投影和斜投影。
正投影是指投影线与投影平面垂直的投影方式,投影的长度和形状与实物相同;斜投影是指投影线与投影平面倾斜的投影方式,投影的长度和形状与实物可能不同。
在三视图制图中,我们通常使用正投影。
4. 投影视图关系三视图之间存在着特定的相互关系,可以根据某两个视图得出第三个视图。
在主视图和俯视图中,物体的高度和长度的投影是相同的,在主视图中,物体的宽度和高度的投影是相同的;在主视图和侧视图中,物体的宽度和长度的投影是相同的。
5. 欧几里得投影与齐次坐标投影欧几里得投影是一种基于几何学原理的投影方法,直接映射物体的三维坐标到二维平面上;齐次坐标投影是一种基于齐次坐标的投影方法,通过引入齐次坐标,可以将投影转化为矩阵乘法运算,更加方便计算和处理。
6. 投影的投影法线与情况判断在三视图制图中,我们需要根据物体的形状和投影的情况判断物体相对于投影平面的投影法线。
当物体与投影平面平行时,投影法线与投影面平行;当物体边缘垂直于投影平面时,投影法线即为与边缘垂直的线。
7. 投影的可见性在三维物体的投影过程中,由于物体的形状和位置,有些部分的投影可能会被其他部分所遮挡,不能被观察到。
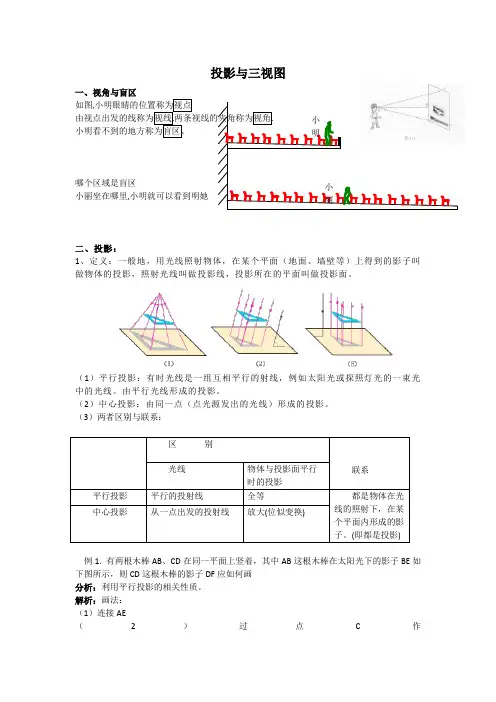
投影与三视图一、视角与盲区如图,小明眼睛的位置称为视点由视点出发的线称为视线,两条视线的夹角称为视角. 小明看不到的地方称为盲区。
哪个区域是盲区 小丽坐在哪里,小明就可以看到明她二、投影:1、定义:一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影,照射光线叫做投影线,投影所在的平面叫做投影面。
(1)平行投影:有时光线是一组互相平行的射线,例如太阳光或探照灯光的一束光中的光线。
由平行光线形成的投影。
(2)中心投影:由同一点(点光源发出的光线)形成的投影。
(3)两者区别与联系:区 别联系 光线物体与投影面平行时的投影 平行投影 平行的投射线 全等都是物体在光线的照射下,在某个平面内形成的影子。
(即都是投影)中心投影从一点出发的投射线放大(位似变换)例1. 有两根木棒AB 、CD 在同一平面上竖着,其中AB 这根木棒在太阳光下的影子BE 如下图所示,则CD 这根木棒的影子DF 应如何画 分析:利用平行投影的相关性质。
解析:画法: (1)连接AE (2)过点C 作小明 小丽CF三视图-画法:根据各形体的投影规律,逐个画出形体的三视图。
画形体的顺序:一般先实(实形体)后空(挖去的形体);先大(大形体)后小(小形体);先画轮廓,后画细节。
画每个形体时,要三个视图联系起来画,并从反映形体特征的视图画起,再按投影规律画出其他两个视图。
对称图形、半圆和大于半圆的圆弧要画出对称中心线,回转体一定要画出轴线。
对称中心线和轴线用细点划线画出。
例2:如下图所示的组合体是由圆柱体和长方体两个基本几何体组成,可分别作出三视图再依情况组合。
三视图例3. 如图所示四棱台ABCD-A1B1C1D1中,上底是边长为2cm的正方形,下底是边长为3cm 的正方形,上、下底面间的距离为2cm ,作出它的三视图。
解析:依题意,可以画出它的三视图如下:主视图左视图俯视图2 cm 3cm 2cm 3cm 2 cm2 cm2 cm2 cm3cm 3cm。

