梯形螺纹连接计算

梯形螺纹计算公式实例讲解梯形螺纹是一种常见的螺纹结构，广泛应用于机械设备和工程领域。

在实际工程中，我们经常需要计算梯形螺纹的尺寸和参数，以便进行加工和安装。

本文将以梯形螺纹的计算公式为例，对梯形螺纹的计算方法进行详细讲解。

梯形螺纹的基本参数包括螺距、螺纹角、螺纹高度、螺纹深度等。

其中，螺距是指螺纹上相邻两条螺旋线之间的距离，通常用P表示；螺纹角是指螺旋线与轴线的夹角，通常用α表示；螺纹高度是指螺纹的顶部到底部的距离，通常用h表示；螺纹深度是指螺纹的凹槽深度，通常用d表示。

梯形螺纹的计算公式如下：1. 螺距P的计算公式：P = π / tan(α)。

2. 螺纹高度h的计算公式：h = P / 2。

3. 螺纹深度d的计算公式：d = h / (tan(α / 2))。

以上三个公式是梯形螺纹计算中最常用的公式，下面我们将通过实例来详细讲解这些公式的应用。

假设我们需要计算一个梯形螺纹的螺距、螺纹高度和螺纹深度，已知螺纹角α为30°，我们可以按照以下步骤进行计算：1. 计算螺距P：根据上面的公式，我们可以得到：P = π / tan(30°) ≈ 3.632P。

2. 计算螺纹高度h：根据上面的公式，我们可以得到：h = P / 2 ≈ 1.816P。

3. 计算螺纹深度d：根据上面的公式，我们可以得到：d = h / (tan(30° / 2)) ≈ 1.048P。

通过以上计算，我们得到了这个梯形螺纹的螺距、螺纹高度和螺纹深度的数值。

这些数值可以帮助我们进行加工和安装，确保螺纹的质量和精度。

除了上面的基本参数计算外，梯形螺纹的计算还涉及到一些其他参数，比如螺纹公差、螺纹长度、螺纹直径等。

这些参数的计算公式和方法也是非常重要的，但由于篇幅限制，我们无法一一进行详细讲解。

感兴趣的读者可以参考相关的专业书籍和资料，深入了解梯形螺纹的计算方法。

总之，梯形螺纹的计算是机械设计和加工中的重要内容，掌握好梯形螺纹的计算方法可以帮助我们更好地进行工程设计和制造。

梯形螺纹参数计算梯形螺纹是一种常见的螺纹结构，它具有特殊的参数计算方法。

本文将介绍梯形螺纹的参数计算方法，并探讨其在工程中的应用。

梯形螺纹的参数计算主要包括螺纹高度、螺距、进给量和螺纹角等。

其中，螺纹高度是指两个相邻螺纹峰值之间的距离，螺距是指螺纹沿轴向前进一个周期所需的长度，进给量是指螺纹沿轴向前进一个周期所需的长度，螺纹角是指螺纹峰值与轴线的夹角。

计算螺距和进给量。

螺距和进给量的计算公式如下：螺距= π × 螺纹直径 / 螺纹分度数进给量 = 螺距× 所有螺纹的螺纹数其中，螺纹直径是指螺纹的最大直径，螺纹分度数是指螺纹的每英寸螺纹数。

接下来，计算螺纹高度。

螺纹高度的计算公式如下：螺纹高度= 0.625 × 螺距计算螺纹角。

螺纹角的计算公式如下：螺纹角 = arctan(螺纹高度/ (π × 螺纹直径))以上就是梯形螺纹的参数计算方法。

在实际工程中，梯形螺纹常用于传递力矩和控制运动，具有较高的传动效率和稳定性。

例如，梯形螺纹可以用于螺杆传动装置，将旋转运动转化为直线运动，广泛应用于工具机、自动化设备和机械传动系统中。

梯形螺纹还可以用于连接和固定零件。

螺纹连接具有可拆卸、紧固可靠的特点，常用于汽车、船舶、飞机等交通工具的组装和维修中。

梯形螺纹的参数计算可以确保螺纹连接的可靠性和稳定性，提高工作效率和安全性。

梯形螺纹是一种常见的螺纹结构，具有特殊的参数计算方法。

通过合理计算螺距、进给量、螺纹高度和螺纹角等参数，可以确保梯形螺纹的性能和可靠性。

在工程中，梯形螺纹广泛应用于传递力矩、控制运动、连接和固定零件等领域，发挥着重要的作用。

希望本文能对读者理解和应用梯形螺纹的参数计算方法有所帮助。

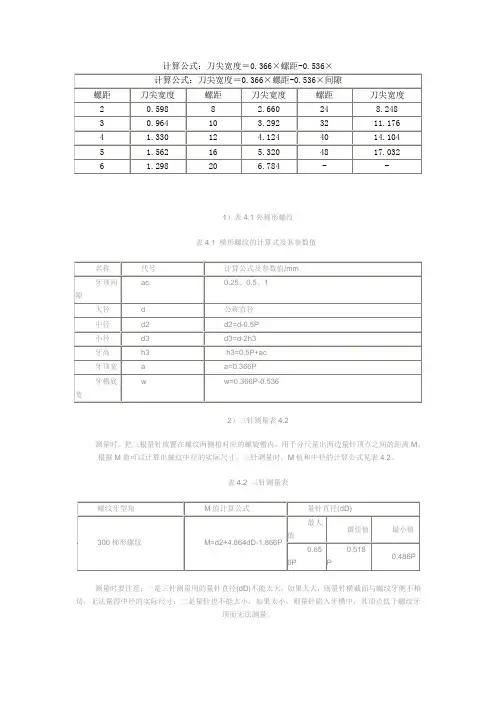
计算公式：刀尖宽度＝0.366×螺距-0.536×
1）表4.1外梯形螺纹
表4.1 梯形螺纹的计算式及其参数值
2）三针测量表4.2
测量时，把三根量针放置在螺纹两侧相对应的螺旋槽内，用千分尺量出两边量针顶点之间的距离M。

根据M值可以计算出螺纹中径的实际尺寸。

三针测量时，M值和中径的计算公式见表4.2。

表4.2 三针测量表
测量时要注意：一是三针测量用的量针直径(dD)不能太大，如果太大，则量针横截面与螺纹牙侧不相切，无法量得中径的实际尺寸；二是量针也不能太小，如果太小，则量针陷入牙槽中，其顶点低于螺纹牙
顶而无法测量。

b）数值计算：
1）梯形螺纹的相关尺寸计算见表4.4：
表4.4梯形螺纹的相关尺寸计算
2）三针测量值
dD最大值=0.656P=0.656×6=3.936mm
dD最佳值=0.518P=0.518×6=3.108mm
dD最小值=0.486P=0.486×6=2.916mm
M=d2+4.864dD-1.866P
=31+4.864×0.518×6-1.866×6
刀具Z向偏置量
设M实测- M理论=2AO1=δ，则A O1=δ/2，且四边形O1O2CE为平行四边形，则ΔAO1O2≌ΔBCE，AO2=EB。

ΔCEF为等腰三角形，则EF=2EB =2AO2。

AO2=AO1×tan(∠AO1O2)=tan15°×δ/2
刀具Z向偏置量EF=2AO2=δ×tan15°=0.268δ。

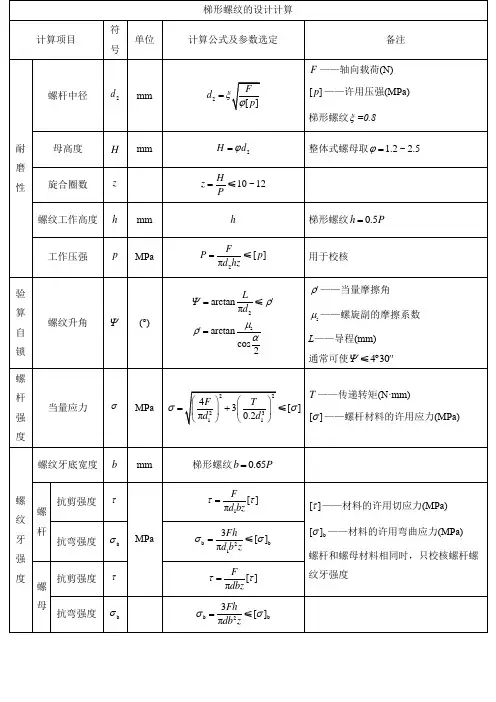
内梯型螺纹计算公式内梯型螺纹是一种常见的螺纹结构，广泛应用于机械设备和工程结构中。

其计算公式是内梯型螺纹设计和制造的重要基础，对于确保螺纹连接的质量和可靠性具有重要意义。

本文将介绍内梯型螺纹的计算公式及其应用。

内梯型螺纹的基本参数包括螺距P、螺纹高度H、螺纹直径d、螺纹角α等。

根据这些参数，可以通过一系列公式来计算内梯型螺纹的各项尺寸。

其中，最常用的计算公式包括螺距P的计算公式、螺纹高度H的计算公式、螺纹直径d的计算公式和螺纹角α的计算公式。

首先是螺距P的计算公式。

螺距P是指相邻两条螺纹之间的距离，通常用毫米（mm）作为单位。

内梯型螺纹的螺距P可以通过以下公式计算得出：P = 1/n。

其中，n为螺纹的线数。

这个公式简单直观，通过线数n的变化可以得到不同螺距P的内梯型螺纹。

其次是螺纹高度H的计算公式。

螺纹高度H是指螺纹的顶部到底部的距离，也是内梯型螺纹的重要尺寸之一。

螺纹高度H可以通过以下公式计算得出：H = P/2 tan(α/2)。

其中，P为螺距，α为螺纹角。

通过这个公式可以直观地看出螺距P和螺纹角α对螺纹高度H的影响。

接下来是螺纹直径d的计算公式。

螺纹直径d是指螺纹的直径，通常也是内梯型螺纹的最大直径。

螺纹直径d可以通过以下公式计算得出：d = D 0.6495P。

其中，D为螺纹的基本直径。

这个公式可以直观地看出螺距P和基本直径D对螺纹直径d的影响。

最后是螺纹角α的计算公式。

螺纹角α是指螺纹的斜面与轴线的夹角，也是内梯型螺纹的重要参数之一。

螺纹角α可以通过以下公式计算得出：tan(α/2) = (P/π) (1/(D/2))。

其中，P为螺距，D为螺纹的基本直径。

通过这个公式可以直观地看出螺距P 和基本直径D对螺纹角α的影响。

除了以上介绍的基本计算公式外，内梯型螺纹的计算还涉及到一些其他参数，如螺纹的公称直径、螺纹的公称长度、螺纹的公称螺距等。

这些参数的计算公式可以根据具体的设计要求和标准来确定。

梯形螺纹三针计算公式梯形螺纹是一种常见的机械连接元件，常用于螺纹连接和传递力矩。

计算梯形螺纹三针的公式可以帮助我们确定适当的尺寸和参数，以确保其安全运行和性能。

首先，我们需要了解梯形螺纹的基本几何特征。

梯形螺纹由一个螺纹轮廓和一条螺纹直径较小的轴向直槽（即三针）组成。

梯形螺纹的关键参数包括螺纹高度h、螺纹角度α、螺纹外径D、螺距P等。

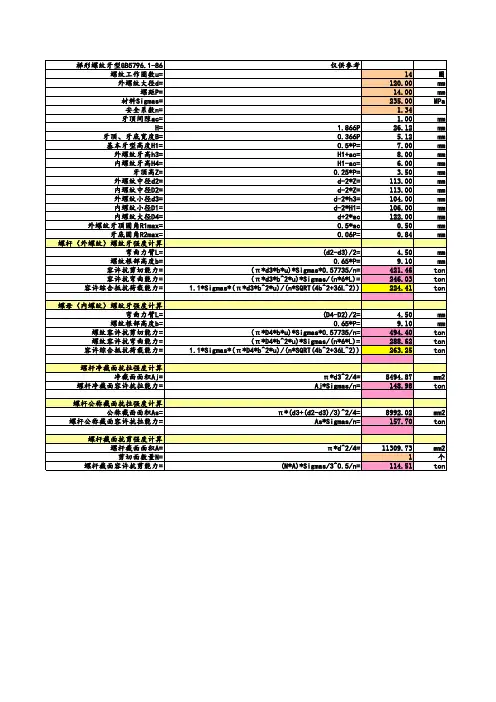
计算梯形螺纹三针的公式可以分为两个方面：扭矩计算和切断计算。

以下是相关参考内容：扭矩计算：1. 安全扭矩计算公式：T = 0.2 * （P * D * h）* μf其中，T表示扭矩，P表示螺距，D表示螺纹外径，h表示螺纹高度，μf表示摩擦系数。

2. 摩擦系数μf的确定：μf = f / (h * P)其中，f表示螺纹公称径向力。

切断计算：1. 切螺纹扭矩的计算公式：Tc = F * D / 2 * sin (α / 2)其中，Tc表示切螺纹扭矩，F表示螺纹公称径向力，D表示螺纹外径，α表示螺纹角度。

2. 轴向力的计算公式：Fa = F * tan (α / 2)其中，Fa表示轴向力，F表示螺纹公称径向力，α表示螺纹角度。

需要注意的是，以上公式仅适用于标准的梯形螺纹，实际应用中还需根据具体情况进行修正。

另外，公式中的参数也需要根据具体设计要求和使用条件进行选择和确定。

除了公式计算，还有一些其他的内容需要注意：1. 材料强度：梯形螺纹的选择还需要考虑材料的强度和耐磨性。

通常情况下，选取材料强度适中且耐磨性好的材料。

2. 表面质量：梯形螺纹表面质量直接影响其摩擦系数和扭矩传递性能。

表面粗糙度要求较高，可以选择研磨或经过特殊的表面处理。

3. 安装和拆卸力矩：在实际使用过程中，还需要考虑拧紧和拆卸时所需的力矩。

根据实际经验，可以合理选择扭矩系数。

综上所述，梯形螺纹三针的计算公式可以帮助我们确定适当的尺寸和参数，但在实际应用中需要综合考虑材料强度、表面质量以及安装和拆卸力矩等因素，确保其安全运行和性能。

梯形螺纹螺棱设计公式
梯形螺纹螺栓是一种常用的连接元件，其设计公式是很重要的。

下面就梯形螺纹螺栓设计公式进行详细介绍。

1. 螺纹参数的表示方法
在设计梯形螺纹螺栓时，需要了解螺栓的参数表示方式：
- P：螺距
- d：螺纹直径
- H：螺纹高度
- h：螺纹顶部高度
- r：圆角半径
- α：螺纹锥角度
2. 基本公式
(1) 螺距P的计算公式：
P = π * d / n
其中n为螺纹数量，通常为1。

(2) 螺纹高度H的计算公式：
H = P / (2 * tan(α / 2))
3. 梯形螺纹螺栓公式的设计原理
梯形螺纹螺栓的设计原理是为了保证螺栓能够正确地连接零件，并且承受特定的拉伸力和扭矩。

通过合理设计螺纹参数和几何尺寸，可以保证螺栓的性能满足设计要求。

4. 螺纹长度的计算
螺纹长度的计算通常需要考虑螺纹的使用情况和紧固要求。

一般来说，螺纹长度等于螺纹直径的2-3倍，以确保螺栓可以正确地连接两个零件，并且在受力时不会出现过度伸长或者过度压缩的情况。

5. 锁紧力的计算
在梯形螺纹螺栓的设计中，锁紧力是一个重要的参数。

一般来说，锁紧力的计算需要考虑螺栓的拉伸量和螺母的阻力。

通过合理的设计螺栓和螺母的参数，可以确保螺栓在受力时不会松动或者过紧，从而保证连接的可靠性。

总结：
梯形螺纹螺栓的设计公式包括螺距、螺纹高度、螺纹长度和锁紧力的计算。

通过合理设计这些参数，可以保证螺栓的性能满足设计要求，从而确保连接的可靠性和安全性。

梯形螺纹尺寸计算公式
梯形螺纹作为一种常见的机械连接件，其尺寸的计算对于设计师和机械工程师来说都非常重要。

下面，我们将为大家介绍梯形螺纹尺寸计算的公式和注意事项。

梯形螺纹一般由一个螺旋体和一个平面组成，其形状类似于一个梯形。

它的尺寸包括螺纹直径、螺纹高度、螺距和齿厚等。

其中，螺距是螺纹在同一方向上重复的间距，齿厚则是梯形螺纹的一条齿的宽度。

梯形螺纹尺寸计算的公式如下：
螺纹高度 H = （D2 - D1）/ 2tanP
螺距P = π cosα /（2H + D1 + D2）
齿厚 t = （D2 - D1）cosα /（2（H + cosα / 2 tanα））其中，D1和D2分别为螺纹外径和内径的直径，α为螺纹斜角，π为圆周率。

计算时需要注意以下几点：
1.在计算时一定要按照标准的公式进行，如果有特殊要求，需要根据实际情况进行计算。

2.在选择螺纹时需要根据实际情况进行选择，以保证产品的安全性和可靠性，不可随意更改。

3.由于梯形螺纹的尺寸较为复杂，建议在计算之前要仔细阅读相关的技术规范和标准，以免发生错误。

4.在进行螺纹加工时一定要严格按照计算结果进行加工，以确保产品符合设计要求。

综上所述，梯形螺纹尺寸计算是机械设计与加工中非常重要的一环，需要严格按照标准规范进行计算和加工，以确保产品的质量和可靠性。

梯形螺纹计算公式梯形螺纹是一种常见的螺纹形状，常用于机械零件的连接和固定。

它的特点是两侧螺纹高度不一致，使得其更容易装拆，且具有良好的抗震性能。

对于梯形螺纹的计算公式，主要包括螺距、螺纹高度、承载力等方面。

首先，梯形螺纹的螺距计算公式如下：S=π*d/P其中，S表示螺距，d表示螺纹直径，P表示螺纹的导程。

螺纹高度的计算公式如下：h=D-d其中，h表示螺纹高度，D表示螺纹大径，d表示螺纹小径。

需要注意的是，梯形螺纹的两侧高度不一致，一侧的高度为h，另一侧的高度为H。

因此，在实际计算时，需要区分两侧的高度。

承载力是一个重要的指标，表示螺纹连接的强度和可靠性。

梯形螺纹的承载力计算公式如下：F=Fr+Fa其中，F表示承载力，Fr表示本体强度，Fa表示接触强度。

本体强度（Fr）的计算公式如下：Fr=As*σs*ηp其中，As表示螺纹轴向截面面积，σs表示材料的抗拉强度，ηp表示载荷系数。

接触强度（Fa）的计算公式如下：Fa=Ac*σr*ηc其中，Ac表示螺纹径向接触面积，σr表示材料的抗剪强度，ηc表示接触系数。

需要注意的是，载荷系数和接触系数会根据实际应用情况进行调整。

载荷系数主要与使用环境和载荷方向有关，接触系数主要与摩擦系数、嵌入系数等因素有关。

此外，还需要根据具体螺纹参数和材料性能来选择合适的材料进行计算。

常用的材料包括碳素钢、合金钢等。

在实际计算中，需要根据材料的力学性能参数来确定材料的抗拉强度、抗剪强度等参数。

总之，梯形螺纹的计算涉及到螺距、螺纹高度、承载力等多个方面。

在实际应用中，需要根据具体情况选择合适的计算公式，并结合材料性能参数进行计算。

这些计算公式可以帮助工程师进行梯形螺纹的设计和评估，以保证其连接和固定的强度和可靠性。

梯形螺纹尺寸计算知乎梯形螺纹是一种常见的螺纹结构，它具有较大的承载能力和良好的自锁性能，广泛应用于机械设备、汽车、航空航天等领域。

梯形螺纹的尺寸计算是设计和制造过程中必不可少的环节，对于确保螺纹的质量和功能起着至关重要的作用。

一、梯形螺纹尺寸的基本要素梯形螺纹的尺寸计算主要包括以下基本要素：1. 螺纹直径（D）：即螺纹的外径，是螺纹连接的基础尺寸。

2. 螺纹节距（P）：即螺纹的螺距，是指相邻两螺纹峰之间的距离。

3. 螺纹高度（H）：即螺纹的高度，是指螺纹的峰到谷的距离。

二、梯形螺纹尺寸计算公式梯形螺纹的尺寸计算涉及到多个参数，需要根据具体的需求和标准来确定。

根据ISO标准，我们可以使用如下的计算公式：1. 螺纹直径（D）的计算公式：D = d - (0.6495 × P)其中，d为螺纹孔直径，P为螺纹节距。

2. 螺纹高度（H）的计算公式：H = 0.6134 × P其中，P为螺纹节距。

三、梯形螺纹尺寸计算的步骤梯形螺纹尺寸的计算步骤如下：1. 确定螺纹直径（D）和螺纹节距（P）的要求。

2. 根据计算公式计算出螺纹直径（D）和螺纹高度（H）。

3. 检查计算结果是否符合要求，如不符合，可以适当调整螺纹直径（D）和螺纹节距（P）的数值，重新计算。

4. 根据计算结果进行螺纹的加工和制造。

四、梯形螺纹尺寸计算的重要性梯形螺纹的尺寸计算对于螺纹连接的质量和可靠性起着至关重要的作用。

如果螺纹尺寸计算不准确，可能导致螺纹连接松动、脱落甚至失效，给设备和人身安全带来严重的风险。

梯形螺纹尺寸计算还涉及到材料的选择和加工工艺的确定。

不同的材料和加工工艺对于螺纹的尺寸要求也有所不同，因此在进行螺纹尺寸计算时，需要考虑这些因素，确保螺纹的质量和可靠性。

梯形螺纹的尺寸计算是设计和制造过程中必不可少的环节，它直接影响螺纹连接的质量和可靠性。

通过正确的计算方法和准确的尺寸参数，可以保证螺纹连接的紧固性和自锁性能，提高设备的使用寿命和安全性。

梯形螺纹中径计算公式
梯形螺纹是一种常用的机械连接螺纹，用于连接螺母和螺杆。

梯形螺
纹有一个特点，即螺距和螺纹中直径有关系。

在计算梯形螺纹中径时，可
以使用以下公式。

公式1：中径（D）=外径（d）-螺距（P）
其中，外径是指螺母螺纹内径，螺距是指螺纹螺距。

这个公式可以用
于计算一般情况下的梯形螺纹中径。

但是，在使用公式1计算梯形螺纹中径时，通常需要经过一系列的迭
代计算才能得到准确的结果。

这是因为螺距和螺纹中径之间的关系并不是
线性的，而是呈现出一种非线性的关系。

为了更准确地计算梯形螺纹中径，可以使用以下公式。

公式2：中径（D）=外径（d）-αt
其中，α是梯形螺纹的切向系数，t是螺距的张角。

切向系数α是一个比例系数，用于描述螺纹螺距和中径之间的关系。

不同的梯形螺纹具有不同的切向系数。

可以通过查表的方式获得不同梯形
螺纹的切向系数。

螺距的张角t是螺距的一种度量方式，表示每个螺纹的张角。

张角的
计算公式为：
公式3：张角（t）= arctan（P / πd）
其中，P是螺距，d是外径。

通过公式2和公式3的迭代计算，可以得到准确的梯形螺纹中径。

总结起来，梯形螺纹中径的计算公式为：
公式2：中径（D）=外径（d）-αt
公式3：张角（t）= arctan（P / πd）
以上是关于梯形螺纹中径计算的公式和方法的介绍。

希望能对您有所帮助。

梯形螺纹计算公式
梯形螺纹是一种双线螺纹形式，其特点是外螺纹面具有梯形斜面，梯形螺纹的特点是可以减少摩擦，减少拧紧力矩，从而改善拧紧效率和拧紧质量。

梯形螺纹计算公式是用来计算梯形螺纹尺寸的精确方法，以确保螺纹的正确尺寸和正确的拧紧力矩。

梯形螺纹计算公式的正确使用有助于减少螺纹的损失和拧紧的失败。

它的计算公式为：
h = 0.6 * π * P * t
其中，h是梯形螺纹斜面的高度，π是圆周率，P是螺纹的模数，t 是螺纹的螺距。

梯形螺纹的计算公式可以帮助用户正确测量螺纹的尺寸，有效地改善拧紧效率和拧紧质量。

它还可以帮助用户确定螺纹的合适拧紧力矩，以避免螺纹损坏和拧紧失败。

此外，梯形螺纹计算公式还可以帮助用户计算梯形螺纹的最大拧紧力矩和螺纹的最小拧紧力矩，确保螺纹的安全拧紧。

总之，梯形螺纹计算公式可以帮助用户计算准确的螺纹尺寸，改善拧紧效率和拧紧质量，确定合适的拧紧力矩，以避免螺纹损坏和拧紧失败，确保梯形螺纹的安全拧紧。

梯形螺纹强度梯形螺纹强度是螺纹连接件的一项重要性能指标，是指连接件在受到一定载荷时不发生失效或破坏的能力。

由于梯形螺纹连接具有优良的耐疲劳、耐腐蚀、承载能力强等特点，因此广泛应用于各种机械、设备、建筑等领域中。

本文将从梯形螺纹连接的特点、强度计算方法和提升梯形螺纹强度的措施等方面进行分析。

一、梯形螺纹连接的特点梯形螺纹连接与普通的机械连接相比，具有以下优点：1. 承载能力强梯形螺纹连接的承载能力强，能够承受大的拉伸或剪切力，具有优异的机械性能。

2. 重复使用性好梯形螺纹连接在正常使用情况下，能够进行多次拆卸和安装，具有良好的重复使用性。

3. 圆度误差小梯形螺纹连接采用梯形剖面设计，具有较小的圆度误差，使得连接紧密，不易松动。

4. 适用性广梯形螺纹连接适用于不同工作环境和不同工作条件下的场合，具有广泛的适用性。

梯形螺纹连接的强度计算主要包括以下几个方面：1. 拉伸强度拉伸强度指连接件在受到拉伸载荷时，不发生破坏的能力。

梯形螺纹连接的拉伸强度计算公式为：σt = Fi / (π * d * p)其中，σt为梯形螺纹连接的拉伸强度，Fi为连接件承载的拉伸载荷，d为螺杆直径，p为梯形螺纹的节距。

2. 剪切强度3. 接触强度为了提高梯形螺纹连接的强度，可以采取以下的措施：1. 优化设计在梯形螺纹连接的设计中，应该尽可能减少下方浅槽的高度，使得剖面的半角更加尖锐，以提升连接的承载能力。

2. 采用高强度材料3. 热处理加工采用热处理工艺，可以对梯形螺纹连接进行强度加固，使得连接的承载能力得到提升。

4. 加装防松垫片在一些高振动、高压力的场合中，可以在梯形螺纹连接中加装防松垫片，从而增强连接的紧固性和抗松动性。

总之，梯形螺纹连接作为机械连接中的一种重要形式，其强度是保证连接可靠性的重要指标，采取适当的措施提升梯形螺纹连接的强度，将大大提高连接的安全性和可靠性。

梯形螺纹计算公式实例分析梯形螺纹是一种常见的机械连接元件，它具有良好的承载能力和自锁性能，广泛应用于机械设备和工程结构中。

在设计和制造梯形螺纹时，需要对其进行计算，以确保其符合工程要求。

本文将以梯形螺纹的计算公式为例，对其进行详细分析和实例演示。

梯形螺纹的计算公式主要涉及到以下几个方面，螺距的计算、螺纹剖面的计算、螺纹强度的计算等。

下面将分别对这些方面进行详细介绍。

首先是螺距的计算。

梯形螺纹的螺距是指螺纹线上相邻两点之间的距离，通常用P表示。

梯形螺纹的螺距可以通过以下公式进行计算：P = π d / n。

其中，P为螺距，π为圆周率，d为螺纹直径，n为螺纹的导程。

通过这个公式，可以方便地计算出梯形螺纹的螺距，为后续的设计和制造提供基础数据。

其次是螺纹剖面的计算。

梯形螺纹的剖面通常为三角形，其内外径随着螺距的增大而增大。

螺纹的内外径可以通过以下公式进行计算：d2 = d 0.6495 P。

d1 = d 1.2268 P。

其中，d1为螺纹的内径，d2为螺纹的外径，P为螺距。

通过这个公式，可以方便地计算出梯形螺纹的内外径，为螺纹的加工提供参考。

最后是螺纹强度的计算。

梯形螺纹在实际工作中需要承受一定的载荷，因此其强度是设计和制造中需要重点考虑的问题。

梯形螺纹的强度可以通过以下公式进行计算：σ = 2 F / (π d P)。

其中，σ为螺纹的强度，F为螺纹所承受的载荷，d为螺纹直径，P为螺距。

通过这个公式，可以方便地计算出梯形螺纹的强度，为工程设计提供参考。

以上就是梯形螺纹的计算公式的简要介绍，下面将通过一个实例来演示这些计算公式的应用。

假设有一台机械设备，需要使用梯形螺纹来实现传动和定位。

根据设备的工作要求，需要计算出梯形螺纹的螺距、螺纹剖面和强度。

设备的工作载荷为1000N，螺纹直径为20mm。

首先计算螺距。

根据上面的公式，可以得出：P = π 20 / 4 = 15.71mm。

接下来计算螺纹剖面。

根据上面的公式，可以得出：d2 = 20 0.6495 15.71 = 9.62mm。

梯形螺纹三针测量计算公式梯形螺纹三针测量计算公式是用来测量梯形螺纹的一种方法。

梯形螺纹是一种常见的机械连接件，广泛应用于各种机械设备中。

梯形螺纹的测量对于保证设备的质量和准确性非常重要。

本文将介绍梯形螺纹三针测量计算公式的原理和应用，以及如何进行测量。

梯形螺纹的主要参数有螺纹高度h，螺距p，螺纹深度d，螺纹角α等。

在进行梯形螺纹的测量时，需要使用三根测量针分别测量螺纹的上顶径D1，下顶径D2和螺纹的最小径d3。

根据这些测量值可以计算出梯形螺纹的各个参数。

首先，我们来介绍一下梯形螺纹的基本几何关系。

梯形螺纹的螺距p等于上顶径D1和下顶径D2的差值。

螺纹深度d等于上顶径D1与最小径d3的差值。

螺纹角α可以通过螺纹高度h 和螺距p的比值来计算。

根据上述几何关系，我们可以得到以下的计算公式：螺距p = D1 - D2螺纹深度d = D1 - d3螺纹角α = arctan(h/p)其中，arctan是反正切函数，可以通过计算器或数学软件来求得。

在进行梯形螺纹的测量时，需要注意以下几点：使用合适的测量工具，如测微计、千分尺等，保证测量的精度和准确性。

在测量前，需要先清洁螺纹的表面，确保没有杂质和污垢的影响。

测量针的选择要适合螺纹的尺寸，太粗或太细都会影响测量的准确性。

测量时要保持针与螺纹的接触紧密，避免产生误差。

在实际应用中，梯形螺纹的测量通常是通过机械测量仪器来完成的。

这些测量仪器可以自动计算出梯形螺纹的各个参数，并显示在仪器的屏幕上。

这样不仅提高了测量的速度和准确性，还可以减少人为操作的误差。

总结起来，梯形螺纹三针测量计算公式是一种常用的测量方法，可以用来测量梯形螺纹的各个参数。

通过测量针的测量值，可以计算出螺距、螺纹深度和螺纹角等参数。

在进行测量时，需要注意选择合适的测量工具和测量针，保持测量的精度和准确性。

同时，机械测量仪器的应用可以提高测量的效率和准确性。

这些方法和技巧在实际生产中都有广泛的应用，对于保证产品的质量和准确性起到了重要的作用。

梯形螺纹计算公式实例梯形螺纹是一种常见的机械连接元件，广泛应用于机械设备和工程结构中。

在工程设计和制造过程中，对梯形螺纹的计算和设计是非常重要的。

本文将介绍梯形螺纹的计算公式，并通过实例进行详细说明。

梯形螺纹的基本参数包括螺距、螺纹角、螺纹高度等。

在进行梯形螺纹的计算时，需要根据这些参数来确定螺纹的尺寸和性能。

下面将分别介绍梯形螺纹的计算公式及其实例。

1. 螺距的计算公式。

梯形螺纹的螺距是指相邻两螺纹峰顶之间的距离，通常用P表示。

螺距的计算公式如下：P = π d / tan(α)。

其中，d为螺纹直径，α为螺纹角。

例如，当螺纹直径d=20mm，螺纹角α=30°时，可通过上述公式计算得到螺距P=36.63mm。

2. 螺纹高度的计算公式。

梯形螺纹的螺纹高度是指螺纹的顶部到底部的距离，通常用H表示。

螺纹高度的计算公式如下：H = P / (2 tan(α))。

例如，当螺距P=36.63mm，螺纹角α=30°时，可通过上述公式计算得到螺纹高度H=31.80mm。

3. 螺纹公称直径的计算公式。

梯形螺纹的公称直径是指螺纹的基本直径，通常用d表示。

螺纹公称直径的计算公式如下：d = D 0.64952 P。

其中，D为公称直径。

例如，当公称直径D=20mm，螺距P=36.63mm时，可通过上述公式计算得到螺纹公称直径d=17.57mm。

4. 螺纹的剖面尺寸的计算公式。

梯形螺纹的剖面尺寸包括螺纹峰高、螺纹谷深等参数。

这些参数的计算公式较为复杂，一般需要借助专业的螺纹标准或软件来进行计算。

通过上述计算公式的实例，我们可以清晰地了解梯形螺纹的计算方法。

在实际工程中，对梯形螺纹的计算和设计需要综合考虑材料、载荷、工作环境等多方面因素，以确保螺纹连接的可靠性和稳定性。

除了上述基本参数的计算外，还需要对螺纹的强度、密封性、耐磨性等性能进行评估和计算。

这些计算公式和方法需要结合具体的工程要求和实际情况进行综合分析和计算。