常用几何作图方法

常见几何图形的作图方法正多边形的画法斜度和锥度椭圆的画法圆弧连接正多边形的画法1.正六边形画法利用外接圆半径作图正多边形的画法1.正六边形画法已知外接圆直径，利用圆规、三角板作图。

正多边形的画法1.正六边形画法已知外接圆直径，利用丁字尺、三角板作图。

正多边形的画法1.正六边形画法已知外接圆直径，利用丁字尺、三角板作图。

正多边形的画法1.正六边形画法已知对边距离作图正多边形的画法1.正六边形画法已知对边距离作图正多边形的画法2.正五边形画法已知外接圆直径作图正多边形的画法2.正五边形画法已知外接圆直径作图正多边形的画法3.正n边形画法已知外接圆直径作图正七边形为例正多边形的画法3.正n边形画法已知外接圆直径作图正七边形为例斜度和锥度1.斜度斜度的画法举例画出作图基准线 作斜度1:5辅助线BA 求出AB 两点线 BA作辅助线的平行线 加深、标注尺寸斜度和锥度1.斜度斜度的画法举例画出作图基准线作斜度1:5辅助线求出AB两点线作辅助线的平行线加深、标注尺寸斜度和锥度2.锥度锥度的画法举例画出作图基准线 作锥度1:5辅助线 BA求出AB 两点线 作辅助线的平行线 加深、标注尺寸BA斜度和锥度2.锥度锥度的画法举例画出作图基准线 作锥度1:5辅助线 求出AB 两点线 作辅助线的平行线 加深、标注尺寸BA1:5椭圆的画法已知椭圆长轴AB、短轴CD。

四心圆弧法椭圆的画法已知椭圆长轴AB、短轴CD 。

四心圆弧法圆弧连接绘制机器零件轮廓时，常遇到一条线段（直线或曲线）光滑地过渡到另一条线段的情况。

如图中的R8把圆弧和直线光滑连接起来，R10把两段直线光滑的连接起来。

这种用圆弧光滑地连接相邻两线段的方法称为圆弧连接。

圆弧连接１．圆弧连接的基本作图原理圆弧与直线相切圆弧与圆弧外切圆弧与圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧连接两直线圆弧连接２．圆弧连接的基本作图方法圆弧连接两直线圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧外切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧外切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧连接一直线一圆弧圆弧连接２．圆弧连接的基本作图方法圆弧连接一直线一圆弧小结正多边形的画法斜度和锥度椭圆的画法圆弧连接。

数学方法：初中几何五种作图的基本概念及技巧梳理汇总一、基本概念1.尺规作图：在几何里，用没有刻度的直尺和圆规来画图，叫做尺规作图。

2.基本作图：最基本、最常用的尺规作图，通常称基本作图。

3.五种常用的基本作图：(1)作一条线段等于已知线段；(2)作一个角等于已知角；(3)平分已知角；(4)作线段的垂直平分线．(5)经过一点作已知直线的垂线4.掌握以下几何作图语句：(1)过点×、点×作直线××；或作直线××，或作射线××；(2)连结两点×、×；或连结××；(3)在××上截取××=××；(4)以点×为圆心，××为半径作圆（或弧）；(5)以点×为圆心，××为半径作弧，交××于点×；(6)分别以点×、点×为圆心，以××、××为半径作弧，两弧相交于点××；(7)延长××到点×，或延长××到点×，使××=××．5.学过基本作图后，在以后的作图中，遇到属于基本作图的地方，只须用一句话概括叙述就可以了，如：(1)作线段××=××；(2)作∠×××=∠×××；(3)作××（射线）平分∠×××；(4)过点×作××⊥××，垂足为×；(5)作线段××的垂直平分线××．二、五种基本作图方法演示：尺规作图的基本步骤和作图语言一、作线段等于已知线段：已知：线段a求作：线段AB，使AB＝a作法：。

初二数学 五种基本作图（一）基本概念1.尺规作图：在几何里，用没有刻度的直尺和圆规来画图，叫做尺规作图。

2.基本作图：最基本、最常用的尺规作图，通常称基本作图。

3.五种常用的基本作图：(1)作一条线段等于已知线段；(2)作一个角等于已知角；(3)平分已知角；(4)作线段的垂直平分线。

(5)经过一点作已知直线的垂线4.掌握以下几何作图语句：(1)过点×、点×作直线××；或作直线××，或作射线××；(2)连结两点×、×；或连结××；(3) 在××上截取××=××；(4)以点×为圆心，××为半径作圆（或弧）；(5)以点×为圆心，××为半径作弧，交××于点×；(6)分别以点×、点×为圆心，以××、××为半径作弧，两弧相交于点××；(7)延长××到点×，或延长××到点×，使××=××。

5.学过基本作图后，在以后的作图中，遇到属于基本作图的地方，只须用一句话概括叙述就可以了，如：(1)作线段××=××；(2)作∠×××=∠×××；(3)作××（射线）平分∠×××；(4)过点×作××⊥××，垂足为×；(5)作线段××的垂直平分线××。

第三节 几何作图[Geometrical Construction]一、等分直线段 [Dividing a Line into Equal Parts]将AB 直线段n 等份，作图方法如图1-21所示。

二、等分两平行线间的距离 [Dividing the Distance Between Two ParallelLines into Equal Parts]等分两平行线AB 、CD 之间的距离的作图方法如图1-22所示。

(以五等分为例)(a ) 已知直线段AB (b ) 过A 点做辅助线AM ，以适当长为单位，在AM 上量取n 等份，得1，2，…，K 点 (c ) 连接KB ，过1，2，…作KB 的平行线与AB 相交，即可将AB 分为n 等份图1-21 等分线段为n等份(a ) 已知平行线AB 、CD(b) 置直尺0点于CD 上，转动尺身，使刻度5落在AB 上，截得1、2、3、4各等分点(c ) 过各分等点分别作已知直线AB 的平行线，即得所求图1-22 等分两平行线之间的距离(a ) 按踏步级等分梯段的总高度，并确定梯段的总宽度EF(b ) 作E 1F 1，E 1F 1与各水平线的交点作垂线，即得各踏步级(c ) 清理图面，加深图线图1-23利用等分两平行线之间的距离的方法作踏步等分两平行线之间的距离的作图方法，常用于画台级或楼梯。

画图时先按台级或楼梯的级数等分该梯段的总高度，画出每级高度，若踏面总宽度为EF ，则可作E 1F 1，E 1F 1与各水平线的交点作垂线，即得各踏步级，如图1-23所示。

三、坡度的画法 [Drawing a Slope]坡度是指一直线或平面对另一直线或平面的倾斜程度，其大小用直线或平面间夹角的正切来表示。

在图样中以1∶n 的形式标注。

图1-24为坡度1∶n 的作图方法及标注。

标注坡度是，应加注坡度“” 1-6“坡度”。

四、正多边形的画法 [Drawing Regular Polygons]由于正多边形的边数不同，其画法各异。

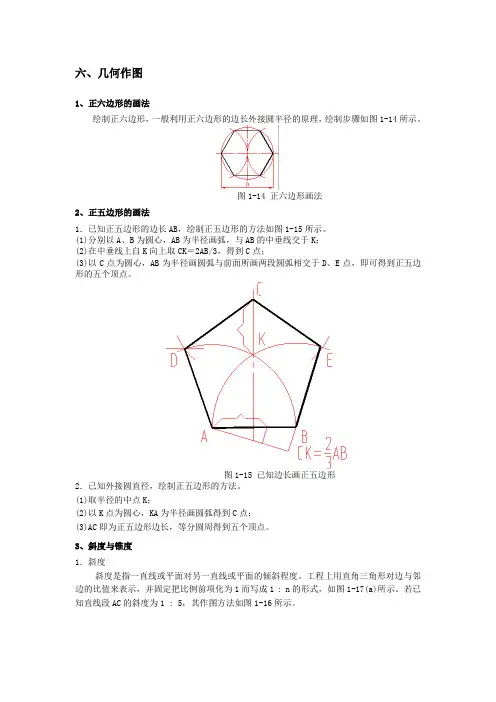
六、几何作图1、正六边形的画法绘制正六边形，一般利用正六边形的边长外接圆半径的原理，绘制步骤如图1-14所示。

图1-14 正六边形画法2、正五边形的画法1．已知正五边形的边长AB，绘制正五边形的方法如图1-15所示。

(1)分别以A、B为圆心，AB为半径画弧，与AB的中垂线交于K；(2)在中垂线上自K向上取CK＝2AB/3，得到C点；(3)以C点为圆心，AB为半径画圆弧与前面所画两段圆弧相交于D、E点，即可得到正五边形的五个顶点。

图1-15 已知边长画正五边形2．已知外接圆直径，绘制正五边形的方法。

(1)取半径的中点K；(2)以K点为圆心，KA为半径画圆弧得到C点；(3)AC即为正五边形边长，等分圆周得到五个顶点。

3、斜度与锥度1．斜度斜度是指一直线或平面对另一直线或平面的倾斜程度。

工程上用直角三角形对边与邻边的比值来表示，并固定把比例前项化为1而写成1 : n的形式，如图1-17(a)所示。

若已知直线段AC的斜度为1 : 5，其作图方法如图1-16所示。

图1-16斜度的画法2．锥度锥度是指圆锥的底圆直径D与高度H之比，通常，锥度也要写成1 : n的形式。

锥度的作图方法如图1-17所示。

图1-17 锥度的画法4、圆弧连接圆弧与圆弧的光滑连接，关键在于正确找出连接圆弧的圆心以及切点的位置。

由初等几何知识可知：当两圆弧以内切方式相连接时，连接弧的圆心要用R－R0来确定；当两圆弧以外切方式相连接时，连接弧的圆心要用R＋R0来确定。

用仪器绘图时，各种圆弧连接的画法如图1-18所示。

这些作图方法在计算机绘图中实现起来既准确又快捷，充分体现了计算机高速和精确的特点。

(a)用圆弧连接两已知直线 (b) 用圆弧连接直线和圆弧(c)与两圆弧外切的画法 (d)与两圆弧内切的画法图1-18 圆弧连接5、椭圆和渐开线的画法1．椭圆的近似画法常用的椭圆近似画法为四圆弧法，即用四段圆弧连接起来的图形近似代替椭圆。

如果已知椭圆的长、短轴AB、CD，则其近似画法的步骤如下：(1)连AC，以O为圆心，OA为半径画弧交CD延长线于E，再以C为圆心，CE为半径画弧交AC于F；(2)作AF线段的中垂线分别交长、短轴于O1、O2，并作O1、O2的对称点O3、O4，即求出四段圆弧的圆心，如图1-19所示。

初二尺规作图五个方法
尺规作图，是一种利用尺规来绘制图形的一种方法。

它包括五种方法：
一、直线图法：用尺规将两个点之间的直线绘制出来，即可构成图形。

可以用来绘制简单的几何图形，如矩形、梯形、三角形等。

二、折线图法：用尺规将多个点之间的折线绘制出来，即可构成图形。

可以用来绘制复杂的曲线图形，如抛物线、椭圆等。

三、圆弧图法：用尺规将一个圆或一些圆弧绘制出来，即可构成图形。

可以用来绘制圆形的几何图形，如圆、圆环等。

四、线环图法：用尺规将一个线环绘制出来，即可构成图形。

可以用来绘制复杂的几何图形，如圆环、环形等。

五、投影法：用尺规将投影绘制出来，即可构成图形。

可以用来绘制立体图形，如体积图、投影图等。

以上就是尺规作图的五种方法。

尺规作图是一种简单实用的绘图方法，可以用来绘制各种几何图形和立体图形。

它的最大优势在于可以准确控制作图的尺寸和准确性，从而获得精确的图形。

由于尺规作图的优点，在日常工作中，它被广泛应用于设计图纸、绘制图形等方面。

尺规作图的五种方法都是绘图中必不可少的工具，因此，在绘制图形时，应该根据自身的需求充分考虑这五种方法，以求最佳的作图效果。

初中尺规作图基本方法
尺规作图是绘制平面几何图形的一种重要方法，初中阶段主要涉及到以下四种基本作图：
1. 线段作图：给出一条直线段AB，要求在这个线段上取一点P，使AP：PB=2:3。

（具体方法：先作出线段AB，然后以A 为圆心，以AB 为半径画一个圆，再以B 为圆心，以BA 为半径画一个圆，两圆交点记为P，连接AP、PB即可）
2. 直角三角形作图：给定一个直角三角形，要求在某一边上取一点，使该点到此边的距离为另一条直角边的一半。

（具体方法：先作出直角三角形ABC，然后以AB 为直径画一个半圆，半圆上一点记为D，连接BD，把BD 延长至E，使BE=BD，连接CE，设置长为BE 的尺子，从点C 开始，把尺子逐步向E 滑动，途中记录一点F，使CF=BE，连接AF，即为所求点）
3. 等边三角形作图：给定一条直线段AB，要求在这个线段上取一点P，使三角形PAB 为等边三角形。

（具体方法：先作出线段AB，然后以A 为圆心，以AB 为半径画一个圆，再以B 为圆心，以BA 为半径画一个圆，两圆交点分别记为P、Q，连接PQ，以PQ 为边取一等边三角形PQR，PQ 与AB 的交点即为所求点）
4. 正方形作图：给定一条直线段AB，要求在这个线段上取一点P，使PABQ 为
正方形。

（具体方法：先作出线段AB，然后以A 为圆心，以AB 为半径画一个圆，再以B 为圆心，以BA 为半径画一个圆，两圆交点分别记为P、Q，连接PQ，将PQ 延长至R，使PR=AB，连接AR、BR，即可得到正方形PABQ）。