1.3常用的几何作图方法解析

高中数学几何作图解析几何的绘图技巧在高中数学的学习中，解析几何无疑是一个重点和难点。

而熟练掌握绘图技巧对于解决解析几何问题往往能起到事半功倍的效果。

接下来，就让我们一起深入探讨一下这其中的绘图技巧。

首先，我们要明确绘图的基本工具。

通常情况下，我们会用到直尺、圆规、铅笔等。

在作图之前，一定要确保工具准备齐全并且完好无损，以免影响作图的准确性。

对于直线的绘制，我们要先确定直线上的两个点。

一般可以通过给定的直线方程，求出两个特定的点的坐标，然后用直尺将这两点连接起来。

比如，对于直线方程 y ＝ 2x ＋ 1，我们可以令 x ＝ 0，求出 y＝ 1，得到点(0, 1)；再令 x ＝ 1，求出 y ＝ 3，得到点(1, 3)。

通过连接这两个点，就能画出这条直线。

在绘制圆的时候，圆规就派上用场了。

如果已知圆的圆心坐标和半径长度，那么将圆规的一只脚放在圆心处，调整圆规两脚的距离为半径长度，然后绕着圆心旋转一周，就能画出一个完整的圆。

比如，圆心为(2, －1)，半径为 3 的圆，我们就可以按照这个方法准确地画出。

椭圆的绘制相对复杂一些。

我们可以根据椭圆的标准方程来确定椭圆的长半轴 a 和短半轴 b。

然后，以椭圆的中心为原点，分别在 x 轴和y 轴上截取长度为 2a 和 2b 的线段。

通过这四个点，可以大致勾勒出一个矩形，这个矩形被称为椭圆的“外接矩形”。

接着，使用平滑的曲线将矩形的四个顶点连接起来，尽量使曲线靠近矩形的边缘，就可以画出一个椭圆。

双曲线的绘制方法与椭圆有相似之处，但也有不同。

同样根据双曲线的标准方程确定实半轴 a 和虚半轴 b。

先画出两条分别经过中心，且与 x 轴和 y 轴夹角分别为渐近线斜率的直线，这两条直线就是双曲线的渐近线。

然后以中心为对称点，在渐近线的两侧分别画出双曲线的两支。

在绘图过程中，准确标记坐标和关键的数值是非常重要的。

这不仅有助于我们清晰地理解图形，还能方便后续的计算和分析。

比如在绘制直线时，要标记出所取点的坐标；在绘制圆、椭圆和双曲线时，要标记出圆心、半轴的长度等。

初三数学几何作图步骤与技巧数学几何作图是初三数学中的重要内容，它在培养学生的空间想象力和逻辑思维能力方面起着重要作用。

下面将结合几何作图的基本步骤和技巧，为大家介绍初三数学几何作图的方法。

一、几何作图的基本步骤几何作图有一定的规范和步骤，下面将给出几何作图的基本步骤：1. 题目分析：仔细阅读题目，理解图形特征和要求。

2. 绘制基础线段：根据给定的条件，画出基础线段，如已知的直线段、线段比例、等分线段等。

3. 作出必要角度：根据题目要求和给定条件，画出必要的角度，如已知的垂直角、等角等。

4. 确定图形位置：根据条件和图形特征，确定图形的位置与大小。

5. 作出其他线段和角度：根据已知的条件，分析图形特征，作出其他线段和角度。

6. 检查与判断：检查所绘制的图形是否满足条件和要求，根据需要进行修正。

7. 写明过程：在纸上清晰地写出作图的步骤和关键点。

8. 作图尺规化：对于需要使用尺规作图的题目，还需要用尺规器进行作图。

二、几何作图的技巧除了基本的作图步骤外，还有一些技巧可以帮助我们更好地完成几何作图。

1. 合理利用已知条件：在作图之前，仔细分析已知条件和题目要求，合理利用已知条件来确定作图的重点和方向。

2. 尺子的运用：在使用尺子时要注意尺子与纸张之间的垂直关系，尽量保持尺子平稳，尽量用尺子上的较短刻度进行量度。

3. 判断线段和角度：对于长度或角度不明确的题目，可通过观察图形特征来判断线段的长度和角度的大小。

4. 作图过程中的检查：在作图过程中，不断检查所画的线段和角度是否满足条件和要求，发现错误及时修正。

5. 慎用尺规作图：对于不需要使用尺规作图的题目，尽量避免使用尺规器，以免增加复杂度和出错的可能性。

三、几何作图的注意事项在几何作图过程中，还需要注意以下几点：1. 作图清晰美观：在作图时，要保持图形线条的清晰和整洁，字迹工整，以便读者或老师能够清晰地看出作图步骤和关键点。

2. 作图比例合理：在绘制图形时，要注意线段和角度的比例关系，根据题目要求和已知条件，合理安排图形的大小。

初中数学几何作图基本作图技巧与方法在初中数学的学习中，几何作图是一项重要的技能。

它不仅能够帮助我们更好地理解几何概念和定理，还能培养我们的空间想象力和逻辑思维能力。

接下来，让我们一起深入探讨初中数学几何作图的基本作图技巧与方法。

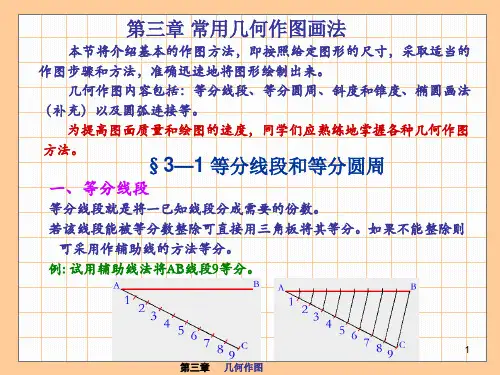
一、线段的作图1、作一条等于已知线段长度的线段首先，我们需要准备好直尺和铅笔。

假设已知线段为 AB，我们要作一条与 AB 长度相等的线段 CD。

步骤如下：（1）用直尺将已知线段 AB 量出长度。

（2）在纸上确定一个起点 C。

（3）将直尺的零刻度线与点 C 对齐，沿着直尺的边缘，从点 C 开始，根据量出的 AB 长度，在直尺相应刻度处标记出点 D。

（4）连接点C 和点D，线段CD 就是与线段AB 长度相等的线段。

2、作线段的平分线作线段的平分线，需要用到圆规。

假设要平分线段 AB。

（1）以点 A 为圆心，大于线段 AB 一半的长度为半径画弧。

（2）再以点 B 为圆心，同样长度为半径画弧，两弧分别交于点 M和点 N。

（3）连接点 M 和点 N，与线段 AB 相交于点 O，点 O 就是线段AB 的中点，直线 MO 就是线段 AB 的平分线。

二、角的作图1、作一个等于已知角大小的角已知角为∠AOB，要作一个与之相等的角∠MON。

步骤如下：（1）先作一条射线 OM。

（2）以点 O 为圆心，任意长为半径画弧，交∠AOB 的两边于点 P和点 Q。

（3）以点 M 为圆心，以 OP 的长为半径画弧，交射线 OM 于点 A'。

（4）以点 A'为圆心，以 PQ 的长为半径画弧，交前弧于点 B'。

（5）过点 B'作射线 ON，则∠MON 就是与∠AOB 相等的角。

2、作角的平分线对于一个角，比如∠AOB，要作其平分线。

（1）以点 O 为圆心，适当长度为半径画弧，分别交 OA、OB 于点C、D。

（2）分别以点 C、D 为圆心，大于二分之一 CD 长为半径画弧，两弧在∠AOB 内部交于点 E。

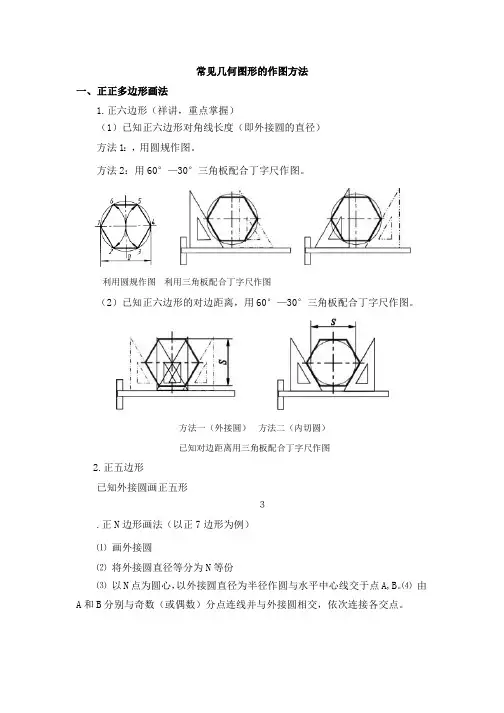
常见几何图形的作图方法正多边形的画法斜度和锥度椭圆的画法圆弧连接正多边形的画法1.正六边形画法利用外接圆半径作图正多边形的画法1.正六边形画法已知外接圆直径，利用圆规、三角板作图。

正多边形的画法1.正六边形画法已知外接圆直径，利用丁字尺、三角板作图。

正多边形的画法1.正六边形画法已知外接圆直径，利用丁字尺、三角板作图。

正多边形的画法1.正六边形画法已知对边距离作图正多边形的画法1.正六边形画法已知对边距离作图正多边形的画法2.正五边形画法已知外接圆直径作图正多边形的画法2.正五边形画法已知外接圆直径作图正多边形的画法3.正n边形画法已知外接圆直径作图正七边形为例正多边形的画法3.正n边形画法已知外接圆直径作图正七边形为例斜度和锥度1.斜度斜度的画法举例画出作图基准线 作斜度1:5辅助线BA 求出AB 两点线 BA作辅助线的平行线 加深、标注尺寸斜度和锥度1.斜度斜度的画法举例画出作图基准线作斜度1:5辅助线求出AB两点线作辅助线的平行线加深、标注尺寸斜度和锥度2.锥度锥度的画法举例画出作图基准线 作锥度1:5辅助线 BA求出AB 两点线 作辅助线的平行线 加深、标注尺寸BA斜度和锥度2.锥度锥度的画法举例画出作图基准线 作锥度1:5辅助线 求出AB 两点线 作辅助线的平行线 加深、标注尺寸BA1:5椭圆的画法已知椭圆长轴AB、短轴CD。

四心圆弧法椭圆的画法已知椭圆长轴AB、短轴CD 。

四心圆弧法圆弧连接绘制机器零件轮廓时，常遇到一条线段（直线或曲线）光滑地过渡到另一条线段的情况。

如图中的R8把圆弧和直线光滑连接起来，R10把两段直线光滑的连接起来。

这种用圆弧光滑地连接相邻两线段的方法称为圆弧连接。

圆弧连接１．圆弧连接的基本作图原理圆弧与直线相切圆弧与圆弧外切圆弧与圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧连接两直线圆弧连接２．圆弧连接的基本作图方法圆弧连接两直线圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧外切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧外切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧连接一直线一圆弧圆弧连接２．圆弧连接的基本作图方法圆弧连接一直线一圆弧小结正多边形的画法斜度和锥度椭圆的画法圆弧连接。

初二数学几何作图基本作图方法与技巧在初二数学的学习中，几何作图是一项非常重要的内容。

它不仅能够帮助我们更直观地理解几何概念和定理，还能培养我们的动手能力和空间想象力。

接下来，就让我们一起来了解一下初二数学几何作图中常见的基本作图方法与技巧。

一、作一条线段等于已知线段这是几何作图中最基础的操作之一。

首先，我们需要准备好直尺和圆规。

步骤如下：1、用直尺画出一条射线。

2、以射线的端点为圆心，以已知线段的长度为半径，用圆规在射线上截取一段，所得到的线段就等于已知线段。

这个作图方法的关键在于圆规半径的调整要准确，以确保作出的线段长度与已知线段相等。

二、作一个角等于已知角这个作图稍微复杂一些，但按照以下步骤来做，也能轻松完成。

1、先作一条射线，作为新角的一边。

2、以已知角的顶点为圆心，任意长为半径画弧，交已知角的两边于两点。

3、以新角一边的端点为圆心，以刚才同样的长度为半径画弧，交新角的这边于一点。

4、以这点为圆心，量取已知角弧上两点之间的距离为半径画弧，与前弧相交。

5、连接新角一边的端点和这个交点，就得到了与已知角相等的角。

在这个作图过程中，要注意每一步的操作都要准确，特别是弧的半径和弧上两点之间距离的量取。

三、作已知线段的垂直平分线垂直平分线的作图在解决很多几何问题时都非常有用。

步骤如下：1、分别以线段的两个端点为圆心，以大于线段一半长度为半径画弧，两弧分别在线段两侧相交。

2、连接这两个交点，所得到的直线就是线段的垂直平分线。

这里要注意圆规半径的选择，一定要大于线段长度的一半，否则两弧可能无法相交。

四、作已知角的平分线角平分线的作图可以帮助我们更好地理解角的性质。

具体步骤：1、以角的顶点为圆心，任意长度为半径画弧，交角的两边于两点。

2、分别以这两个交点为圆心，以大于两点之间距离一半的长度为半径画弧，两弧在角内相交。

3、连接角的顶点和这个交点，这条射线就是角的平分线。

同样，圆规半径的选择要恰当，以保证作图的准确性。

初三数学几何作图技巧分析在初三数学学科中，几何作图是一个非常重要的部分。

几何作图既能够帮助我们更好地理解和掌握几何知识，又能够锻炼我们的思维能力和空间想象力。

本文将对初三数学几何作图的技巧进行详细的分析和探讨。

一、绘制线段在几何作图中，绘制线段是最基本也是最常见的操作。

线段由两个端点确定，我们可以通过以下几种方式进行作图：1. 通过给定的长度绘制线段：当我们知道线段的长度时，可以使用尺规作图或者使用直尺和图钉来绘制线段。

首先，将图纸上的一点作为线段的一个端点，然后按照给定的长度用尺子或者直尺绘制另一个端点，连接两个端点即可得到所求线段。

2. 通过已知线段的平分点绘制线段：当我们知道线段上某个点将线段平分时，可以使用尺规作图或者使用直尺和图钉来绘制线段。

首先，将图纸上的一点作为线段的一个端点，然后在线段上将其平分，连接两个端点即可得到所求线段。

二、作图中的垂直和平行关系在几何作图中，垂直和平行关系是经常出现的。

下面将分别介绍如何作图：1. 绘制垂直线：当我们知道一条直线上某点垂直于另一条直线时，可以使用尺规作图或者使用直尺和图钉来绘制垂直线。

首先，在图纸上画出已知直线，然后以已知直线上某点为顶点，使用直尺或者尺规画出一个90度的角，该角的另一条边与已知直线相交的点即为所求垂直线。

2. 绘制平行线：当我们知道一条直线上某点平行于另一条直线时，可以使用尺规作图或者使用直尺和图钉来绘制平行线。

首先，在图纸上画出已知直线，然后以已知直线上某点为顶点，使用直尺或者尺规画出一个平行于已知直线的线段，该线段的端点即为所求平行线的两个交点。

三、作图中的角的构造角是几何作图中常见的图形，下面将介绍一些常见角的构造方法：1. 绘制等腰三角形：当我们知道一个角是等腰三角形的角时，可以使用尺规作图或者使用直尺和图钉来绘制等腰三角形。

首先，在图纸上画出已知角的两条边，然后以已知角的顶点为圆心，以任意边的长度为半径画一个弧线，在该弧线上再取两个点，这两个点与已知角的两条边等长，连接这两个点与已知角的顶点即可得到所求等腰三角形。

初三数学几何作图技巧分析详解几何作图是初中数学中的重要内容之一，它不仅有助于学生对几何图形的认识和理解，还培养了学生的观察力和逻辑思维能力。

在初三阶段，学生需要掌握一些基本的几何作图技巧，以便能够解决更加复杂的几何问题。

本文将分析并详细解释一些初三数学几何作图的技巧。

一、画三角形三角形是几何学中常见的图形，学生需要学会根据给定条件画出与之相应的三角形。

首先，当我们知道一个三角形的边长时，只需在纸上用直尺依次连接这些点即可画出这个三角形。

其次，如果我们知道一个三角形的底边和底边两边的夹角，可以先画出底边，然后以底边为边用量角器测出夹角，再连接其他两个顶点。

最后，如果我们知道一个三角形的底边和两个底边的对角线，可以先画出底边，然后作出两个对角线，最后连接顶点即可。

二、画正方形和长方形正方形和长方形是几何中的特殊四边形，它们有各自的画法。

首先，当我们知道一个正方形的边长时，只需在纸上用直尺画出四条边相等的线段，然后连接这些线段的端点即可。

其次，如果我们只知道正方形的对角线长度，可以先画出对角线，然后找到对角线中点，以此为圆心作出一个半径为对角线一半长度的圆，最后连接圆上的两个点和对角线的两个端点即可。

对于长方形的画法类似，只需注意各边长度即可。

三、画圆画圆是初三数学中的一个重要环节，同时也是一个相对较难的部分。

学生需要学会根据给定条件画出与之相应的圆。

首先，如果我们知道一个圆的半径或直径，可以以这个半径或直径为边用圆规或者直尺和量角器画出。

其次，如果我们知道一个圆的弦长和弦对应的圆心角，可以先画出弦，然后根据圆心角的大小找到该角平分线，用这条平分线和弦的中点来画出圆。

最后，如果我们知道一个圆的切线和切点，可以先画出切线，然后以切点为圆心，切线长度为半径画出圆。

通过对初三数学几何作图的技巧分析可以发现，几何作图并不是一项难以掌握的技能。

只要我们掌握了画三角形、正方形、长方形和圆的基本画法，再加上一些基本的测量和度量工具，就可以轻松应对各类几何问题。

常见几何图形的作图方法正多边形的画法斜度和锥度椭圆的画法圆弧连接正多边形的画法1.正六边形画法利用外接圆半径作图正多边形的画法1.正六边形画法已知外接圆直径，利用圆规、三角板作图。

正多边形的画法1.正六边形画法已知外接圆直径，利用丁字尺、三角板作图。

正多边形的画法1.正六边形画法已知外接圆直径，利用丁字尺、三角板作图。

正多边形的画法1.正六边形画法已知对边距离作图正多边形的画法1.正六边形画法已知对边距离作图正多边形的画法2.正五边形画法已知外接圆直径作图正多边形的画法2.正五边形画法已知外接圆直径作图正多边形的画法3.正n边形画法已知外接圆直径作图正七边形为例正多边形的画法3.正n边形画法已知外接圆直径作图正七边形为例斜度和锥度1.斜度斜度的画法举例画出作图基准线 作斜度1:5辅助线BA 求出AB 两点线 BA作辅助线的平行线 加深、标注尺寸斜度和锥度1.斜度斜度的画法举例画出作图基准线作斜度1:5辅助线求出AB两点线作辅助线的平行线加深、标注尺寸斜度和锥度2.锥度锥度的画法举例画出作图基准线 作锥度1:5辅助线 BA求出AB 两点线 作辅助线的平行线 加深、标注尺寸BA斜度和锥度2.锥度锥度的画法举例画出作图基准线 作锥度1:5辅助线 求出AB 两点线 作辅助线的平行线 加深、标注尺寸BA1:5椭圆的画法已知椭圆长轴AB、短轴CD。

四心圆弧法椭圆的画法已知椭圆长轴AB、短轴CD 。

四心圆弧法圆弧连接绘制机器零件轮廓时，常遇到一条线段（直线或曲线）光滑地过渡到另一条线段的情况。

如图中的R8把圆弧和直线光滑连接起来，R10把两段直线光滑的连接起来。

这种用圆弧光滑地连接相邻两线段的方法称为圆弧连接。

圆弧连接１．圆弧连接的基本作图原理圆弧与直线相切圆弧与圆弧外切圆弧与圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧连接两直线圆弧连接２．圆弧连接的基本作图方法圆弧连接两直线圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧外切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧外切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧连接一直线一圆弧圆弧连接２．圆弧连接的基本作图方法圆弧连接一直线一圆弧小结正多边形的画法斜度和锥度椭圆的画法圆弧连接。

几何图形画法几何图形是由线段、直线、角度等基本几何元素组成的图形。

通过对这些基本元素的组合使用，可以创造出各种形状的几何图形，如矩形、三角形、圆形等。

在绘制几何图形时，需要掌握一些基本的画法，具体如下：1. 直线的画法直线是几何图形中最基本的元素之一。

在画直线时，需要确定直线的起点和终点，在这两点之间，通过尺子或者其他工具画出一条直线。

如果要使直线更加精细，可以用剪刀剪一张纸片，将其对准直线，然后用铅笔沿着纸片边缘画出一条直线。

2. 角度的画法角度是由两条射线组成的几何图形。

在画角度时，需要确定两条射线的起点和终点，然后用尺子或者其他工具连接这些点，形成两条射线。

接着，需要用圆规和直尺画出一个圆弧，使其与两条射线相切，这样就可以得到所需的角度。

3. 三角形的画法三角形是由三条边和三个角组成的几何图形。

在画三角形时，首先需要确定三个顶点的位置，然后通过连接这些点画出三条边。

在这个过程中，需要确保三条边之间的角度符合要求，以保证所画出的是一个合法的三角形。

4. 矩形的画法矩形是由四条边和四个角组成的几何图形。

在画矩形时，需要确定矩形的长和宽，然后画出两条长边和两条短边。

在画长边和短边的过程中，需要确保它们之间的角度是直角。

5. 圆形的画法圆形是由一个圆心和一组等距离的点组成的几何图形。

在画圆形时，需要确定圆心的位置和圆的半径，然后用圆规画出一个圆弧，使其与圆心相切。

通过不断重复这个过程，可以得到一个完整的圆形。

绘制几何图形时，还需要注意以下几点：1. 确定尺寸：在绘制几何图形时，需要明确每个元素的长度、角度等尺寸参数，以确保所画出的图形符合要求。

2. 使用合适的工具：在画直线、角度、圆弧等元素时，需要选择合适的工具，以确保画出的图形精细、清晰。

3. 练习基本技能：几何图形的绘制需要掌握一些基本的技能，如使用尺子、圆规等工具，画直线、角度等元素，需要不断加强练习。

总之，准确、精细绘制几何图形需要掌握基本的绘图技能和细心认真的态度。