(word完整版)平行与垂直的知识点总结,推荐文档

空间中的平行与垂直例题和知识点总结在立体几何的学习中，空间中的平行与垂直关系是非常重要的内容。

理解和掌握这些关系，对于解决相关的几何问题具有关键作用。

下面我们通过一些例题来深入探讨，并对相关知识点进行总结。

一、平行关系（一）线线平行1、定义：如果两条直线在同一平面内没有公共点，则这两条直线平行。

2、判定定理：如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行。

例 1：在正方体 ABCD A₁B₁C₁D₁中，E，F 分别是 AB，BC 的中点，求证：EF∥A₁C₁。

证明：连接 AC，因为 E，F 分别是 AB，BC 的中点，所以 EF∥AC。

又因为正方体中，AC∥A₁C₁，所以 EF∥A₁C₁。

（二）线面平行1、定义：如果一条直线与一个平面没有公共点，则称这条直线与这个平面平行。

2、判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

例 2：已知四棱锥 P ABCD 的底面是平行四边形，M 是 PC 的中点，求证：PA∥平面 MBD。

证明：连接 AC 交 BD 于 O，连接 MO。

因为四边形 ABCD 是平行四边形，所以 O 是 AC 的中点。

又因为 M 是 PC 的中点，所以MO∥PA。

因为 MO⊂平面 MBD，PA⊄平面 MBD，所以 PA∥平面MBD。

（三）面面平行1、定义：如果两个平面没有公共点，则称这两个平面平行。

2、判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

例 3：在正方体 ABCD A₁B₁C₁D₁中，求证：平面 A₁BD∥平面 B₁D₁C。

证明：因为 A₁B∥D₁C，A₁D∥B₁C，且 A₁B 和 A₁D 是平面A₁BD 内的两条相交直线，D₁C 和 B₁C 是平面 B₁D₁C 内的两条相交直线，所以平面 A₁BD∥平面 B₁D₁C。

二、垂直关系（一）线线垂直1、定义：如果两条直线所成的角为 90°，则这两条直线垂直。

平行线与垂直线的知识点总结与归纳
平行线的定义和性质
- 平行线是指在同一个平面内永远不会相交的两条直线。

- 平行线具有以下性质：
1. 平行线之间的距离始终相等。

2. 平行线与同一条横线相交所得的对应角相等。

3. 平行线与同一条截线相交所得的内错角互为补角。

平行线的证明方法
- 直线平行的证明方法包括：
1. 给定两条平行线，通过构造同位角相等的两组对应角来证明。

2. 利用平行线与截线相交所得的内错角互为补角来证明。

3. 利用平行线与横线相交所得的对应角相等来证明。

垂直线的定义和性质
- 垂直线是指在同一个平面内正交相交的两条直线。

- 垂直线具有以下性质：
1. 垂直线之间的夹角为直角（90度）。

2. 垂直线与同一条横线相交所得的对应角互为补角。

平行线与垂直线的关系
- 如果两条直线相互垂直，则它们不能同时是平行线。

- 如果两条直线同时是平行线，则它们不能相互垂直。

平行线和垂直线在几何图形中的应用
- 平行线和垂直线在几何图形中广泛应用，例如：
1. 矩形的四条边两两相互垂直。

2. 平行四边形的对边平行且相等。

3. 平行线切割三角形所得的各部分面积之和等于整个三角形的面积。

以上是关于平行线和垂直线的知识点总结与归纳，希望对您有所帮助。

平行线与垂直线知识点总结平行线和垂直线是几何中重要的概念。

它们之间存在一些关键性的属性和定理，了解这些知识点对于理解几何学的基础原理和解题技巧至关重要。

本文将对平行线和垂直线的定义、性质以及相关定理进行总结。

一、平行线1. 定义：平行线是在同一个平面中，永远不相交的两条直线。

用符号“//”表示两条平行线。

2. 性质：- 平行线之间存在等距离：两条平行线的任意两点之间的距离相等。

- 平行线的斜率相等：两条平行线的斜率是相等的。

- 平行线具有传递性：若直线a//b，b//c，则a//c。

3. 平行线的判定：- 垂直平分线判定法：如果两条线段的中垂线重合，则这两条线段平行。

- 角平分线判定法：如果两条角的角平分线平行，则两条角所在的直线平行。

- 逆否命题判定法：如果两条直线的对应角都不相等，则这两条直线平行。

- 同位角定理：两条平行线被一条横切线所交，所形成的同位角相等。

- 内错角定理：两条平行线被一条横切线所交，所形成的内错角互补。

- 外错角定理：两条平行线被一条横切线所交，所形成的外错角相等。

二、垂直线1. 定义：垂直线是在同一个平面中，相交时所成的角度为90度的两条直线。

2. 性质：- 垂直线之间的角度为90度。

- 垂直线的斜率乘积为-1。

- 垂直线上的任意线段之间距离相等。

3. 垂直线的判定：- 垂直平分线判定法：如果两条线段的中垂线垂直，则这两条线段垂直。

- 互相垂直的直线判定法：如果两条直线斜率的乘积为-1，则这两条直线垂直。

- 同位角定理：两条垂直线被一条直线所交，所形成的同位角相等。

- 内错角定理：两条垂直线被一条直线所交，所形成的内错角互补。

- 外错角定理：两条垂直线被一条直线所交，所形成的外错角相等。

总结：平行线和垂直线是几何学中十分重要的概念。

平行线具有等距离和相等斜率的特点，垂直线具有90度的角度和斜率乘积为-1的特点。

我们可以利用垂直线和平行线的性质来判断线段和直线的关系，以及解决各类几何题目。

平面平行和垂直知识点总结1.定义平面平行: 平面上的两条直线，如果它们的方向相同或重合，则这两条直线是平行的。

平面垂直: 平面上的两条直线，如果它们的方向互相垂直，则这两条直线是垂直的。

2.平行线的性质(1) 两条平行线平行于同一平面；(2) 两条平行线的斜率相同；(3) 平行线上任意一组对应角，必有相等的对应角；(4) 平行线被斜线切割，相交角互补，即对应角相等；(5) 平行线被一条直线所切，对应角相等；(6) 平行线横跨两条直线，内错角、内外角互补；(7) 平行线横跨三条直线，内错角、内外角互补。

3.垂直线的性质(1) 垂直线的斜率乘积为-1；(2) 垂直线必然相交于一点；(3) 垂直线上的任意两组对应角相等；(4) 垂直线被斜线切割，相交角互补，即对应角相等。

4.平面中的垂直线和平行线(1) 垂直线和平行线的关系：平面内一直线和另一直线相互垂直，则这两直线必然平行；(2) 平行线的垂直平分线：若平面上一直线同时是两条平行线的垂直平分线，则这两条平行线必定对称。

5.平行线和垂直线的判定平行线：两条直线斜率相等则平行；或平面内一直线与另一直线相交角相等，则这两直线平行。

垂直线：两条直线相互垂直的条件是它们的斜率乘积为-1；或两条直线的相交角为90度。

6.平面中的平行线和垂直线关系(1) 平面中一条直线被另一直线切割为等角，则这两条直线必然平行；(2) 平面中一条直线被另一直线垂直平分，则这两条直线必然平行。

7.平行线和垂直线的性质应用(1) 平行线性质的应用：在平面上两直线平行，则它们的任意一组对应角相等；或两直线被一直线斜切，则对应角相等。

(2) 垂直线性质的应用：在平面上两直线相互垂直，则它们的任意一组对应角相等。

8.解题技巧(1) 利用斜率判断平行、垂直关系；(2) 利用对应角、内错角、内外角关系判断平行线；(3) 利用斜线的垂直平分性质判断平行关系；(4) 利用斜线的垂直平分性质判断垂直关系。

c c ∥∥b a ba ∥⇒本文档系统总结归纳了立体几何中平行与垂直证明方法，特别适合于高三总复习时对学生构建知识网络、探求解题思路、归纳梳理解题方法。

是一份不可多得的好资料。

一、“平行关系”常见证明方法（一）直线与直线平行的证明1) 利用某些平面图形的特性：如平行四边形的对边互相平行 2) 利用三角形中位线性质3) 利用空间平行线的传递性（即公理4）：平行于同一条直线的两条直线互相平行。

4)利用直线与平面平行的性质定理：如果一条直线与一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

5) 利用平面与平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．6) 利用直线与平面垂直的性质定理：垂直于同一个平面的两条直线互相平行。

abαβba a =⋂⊂βαβα∥ba ∥⇒b a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα βα⊥⊥b a ba ∥⇒αab7) 利用平面内直线与直线垂直的性质：在同一个平面内，垂直于同一条直线的两条直线互相平行。

8) 利用定义：在同一个平面内且两条直线没有公共点（二）直线与平面平行的证明1) 利用直线与平面平行的判定定理：平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行。

2) 利用平面与平面平行的性质推论：两个平面互相平行，则其中一个平面内的任一直线平行于另一个平面。

3) 利用定义：直线在平面外，且直线与平面没有公共点（三）平面与平面平行的证明常见证明方法：1) 利用平面与平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

αbaβαaβαα∥⊂a β∥a ⇒ααββ////∩⊂⊂b a P b a b a =αβ//⇒αβbaPb∥a b a αα⊂⊄α∥a ⇒2)利用某些空间几何体的特性：如正方体的上下底面互相平行等3)利用定义：两个平面没有公共点二、“垂直关系”常见证明方法（一）直线与直线垂直的证明1)利用某些平面图形的特性：如直角三角形的两条直角边互相垂直等。

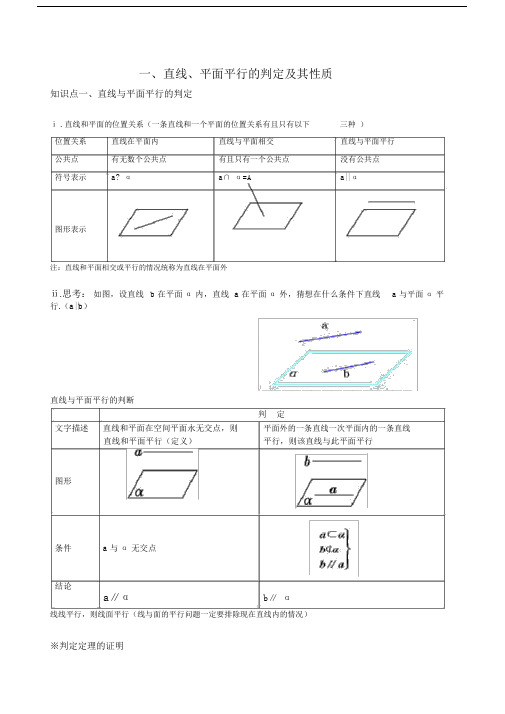
一、直线、平面平行的判定及其性质知识点一、直线与平面平行的判定ⅰ . 直线和平面的位置关系（一条直线和一个平面的位置关系有且只有以下三种）位置关系直线在平面内直线与平面相交直线与平面平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示a? αa∩ α=A a||α图形表示注：直线和平面相交或平行的情况统称为直线在平面外ⅱ.思考：如图，设直线 b 在平面α内，直线 a 在平面α外，猜想在什么条件下直线 a 与平面α平行.（a||b）直线与平面平行的判断判定文字描述直线和平面在空间平面永无交点，则平面外的一条直线一次平面内的一条直线直线和平面平行（定义）平行，则该直线与此平面平行图形条件 a 与α无交点结论a∥αb∥ α线线平行，则线面平行（线与面的平行问题一定要排除现在直线内的情况）※判定定理的证明知识点二、直线与平面平行的性质性质一条直线与一个平面平行，一条直线和一个平面平行，则则这条直线与该平面无交点过这条直线的任一平面与此平面相交，这条直线和交线平行．图形条件a∥ αa∥ αa? βα∩β＝b结论a∩α＝?a∥ b线面平行，则线线平行特别提示证明直线和平面的平行通常采用如下两种方法：①利用直线和平面平行的判定定理，通过“线线”平行，证得“线面”平行；②利用两平面平行的性质定理，通过“面面”平行，证得“线面”平行.知识点三、平面与平面平行的判定判定文字描述如果两个平面无公共一个平面内有两条相如果两个平面同时垂直于点，责成这两个平面平交直线与另一个平面一条直线，那么这两个平行平行，那么这两个平面面垂直。

平行．图形条件，b? βl ⊥αα∩β＝ ? a a∩ b＝ P l ⊥β结论a∥ αb∥αα∥βα∥βα∥β知识点四、平面与平面平行的性质文字描述如果两个平行平面同时和第三平面相交，那么他们的交线平行图形条件α∥ββ∩γ＝ bα∩γ＝ a结论a∥b 性质如果两个平面平行，那么其中一个平面内的直线平行于另一个平面α∥βa? βa∥α二、直线、平面垂直的判定及其性质知识点一、直线和平面垂直的定义与判定定义判定语言描述如果直线l 和平面α内的任意一条直线都垂直，我们就说直线l 与平面互相垂直，记作 l ⊥α一条直线与一个平面内的两条相交直线都垂直，则这条直线与该平面垂直.图形条件 b 为平面α内的任一直线，而 l 对这l ⊥m， l ⊥n，m∩n＝B，m ，一直线总有 l ⊥αn结论l ⊥l ⊥要点诠释：定义中“平面内的任意一条直线” 就是指“平面数条直线”不同（线线垂直线面垂直）内的所有直线”，这与“无知识点二、直线和平面垂直的性质性质语言描述一条直线垂直于一个平面，那么这条直线垂直于同一个平面的两条直线平行.垂直于这个平面内的所有直线图形条件结论知识点三、二面角Ⅰ .二面角：：从一条直线出发的两个半平面所组成的图形叫二面角（dihedral angle） . 这条直线叫做二面角的棱，这两个半平面叫做二面角的面二面角的平面角的三个特征: ⅰ .ⅱ .ⅲ .. 记作二面角点在棱上线在面内与棱垂直－AB－. （简记P－AB －Q ）Ⅱ .二面角的平面角：在二面角－ l －的棱 l 上任取一点O ，以点 O 为垂足，在半平面, 内分别作垂直于棱 l 的射线 OA 和 OB ，则射线 OA 和 OB 构成的AOB 叫做二面角的平面角.作用：衡量二面角的大小；范围：00 1800 .知识点四、平面和平面垂直的定义和判定定义判定文字描述两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面垂直. 一个平面过另一个平面的垂线，则这两个平面垂直图形结果α∩β =lα-l-β=90oα⊥β（垂直问题中要注意题目中的文字表述，特别是“任何”“ 随意”“无数”等字眼）知识点五、平面和平面垂直的性质面面垂直线面垂直（如果两个平面垂直，那么一个平面内垂直于它们交线的直线与一个面平垂直）例题1.如图，若是长方体 ABCD-A1B1C1D1被平面 EFGH截去几何体 EFGHB1C1后得到的几何体，其中 E 为线段 A1B1上异于 B1的点， F 为线段BB1上异于则下列结论中不正确的是A. EH ∥ FGB.四边形EFGH是矩形C.是棱柱B1的点，且EH∥ A1 D 1，D.是棱台2 能保证直线 a 与平面α平行的条件是（A）A.a α ,bα ,a∥b B .bα ,a∥ bC. bα ,c∥α ,a∥ b,a∥cD. bα ,A∈ a,B∈ a,C∈ b ,D∈ b且AC＝BD3 下列命题正确的是（ D F）A. 平行于同一平面的两条直线平行B. 若直线 a∥α , 则平面α内有且仅有一条直线与 a 平行C. 若直线 a∥α , 则平面α内任一条直线都与 a 平行D. 若直线 a∥α , 则平面α内有无数条直线与 a 平行E.如果 a、 b 是两条直线，且 a∥b，那么 a 平行于经过 b 的任何平面F.如果直线a、 b 和平面α满足 a∥ b， a∥α ,bα，那么b∥α4在空间，下列命题正确的是（A ）平行直线的平行投影重合（B ）平行于同一直线的两个平面平行（C ）垂直于同一平面的两个平面平行（ D ）垂直于同一平面的两条直线平行5 已知 m、 n 为两条不同的直线，a、β为两个不同的平面，则下列命题中正确的是A ．m , n , m∥β，n∥βa∥βB ． a∥β，m , n m∥ nC． m⊥ a,m⊥ n n∥ aD ．n∥ m,n⊥ a m⊥ a6.下列命题中错误的是（ A）如果平面⊥平面，那么平面内一定直线平行于平面（ B）如果平面垂直于平面，那么平面内一定不存在直线垂直于平面（ C）如果平面⊥平面，平面⊥平面，l ，那么l⊥平面（ D）如果平面⊥平面，那么平面内所有直线都垂直于平面8.求证：空间四边形相邻两边中点的连线，平行于经过另外两边的平面．已知：空间四边形ABCD 中， E、 F 分别是 AB 、AD 的中点求证： EF‖平面 BCD8题图9题图9.如图，在椎体 P-ABCD 中， ABCD 是边长为 1 的棱形，且∠ DAB=60 ， ,PB=2,E,F 分别是 BC,PC 的中点 .(1)证明： AD ⊥平面 DEF;(2)求二面角 P-AD-B 的余弦值 .课堂练习A组3.m、n 是空间两条不同的直线，α、β是两个不同的平面，下面四个命题中，真命题的序号是________．①m⊥ α， n∥β，α∥ β? m⊥ n；②m⊥n，α∥β，m⊥ α? n∥ β；③m⊥n，α∥β，m∥ α? n⊥ β；④ m⊥ α， m∥ n，α∥ β? n⊥ β.4.如图，在直四棱柱ABCD-A 1 B 1 C 1 D 1中，底面 ABCD 为等腰梯形， AB//CD ，AB=4, BC=CD=2,AA 1 =2,E、E1、F 分别是棱AD、AA 1、AB 的中点。

平行线与垂直线的性质知识点总结平行线与垂直线是几何学中重要的基本概念。

它们在空间中的特性及应用广泛存在于各个领域，包括建筑、工程、地理测量等。

本文将对平行线与垂直线的性质进行总结，并介绍它们的定义、判定方法以及一些常见的应用。

一、平行线的性质1. 定义：在平面上，如果两条直线不相交且在同一个平面内，那么这两条直线被称为平行线。

符号表示为"//"。

2. 判定方法：a. 同位角判定法：当一条直线与两条平行线相交时，对应的同位角相等。

b. 内错角判定法：当一条直线与两条平行线相交时，内错角互补（和为180°）。

3. 平行线的性质：a. 平行线之间没有交点。

b. 平行线与同位角、内错角的关系（根据判定方法）。

c. 平行线与平行线之间的夹角相等。

4. 常见应用：a. 利用平行线的性质进行几何证明。

b. 在地理测量中用于绘制平行线的基准。

二、垂直线的性质1. 定义：在平面上，如果两条直线相交且相交的角度为90°，那么这两条直线被称为垂直线。

符号表示为"⊥"。

2. 判定方法：a. 直角判定法：当两条直线的斜率乘积为-1时，这两条直线互相垂直。

b. 垂直角判定法：当一条直线与两条垂直线相交时，所得的垂直角是相等的。

3. 垂直线的性质：a. 垂直线与同位角、垂直角的关系。

b. 垂直线与平行线之间的夹角为90°。

4. 常见应用：a. 建筑工程中垂直线用于确定垂直方向。

b. 在图形绘制中用于绘制垂直线的基准。

三、平行线与垂直线的关系1. 平行线与垂直线之间的关系：a. 平行线与垂直线是两种互补的关系。

b. 两条直线同时与第三条直线平行，则这两条直线之间也是垂直的。

2. 平行线与垂直线在日常生活中的应用：a. 建筑中，平行线和垂直线的运用可以保证建筑物的稳定和平衡。

b. 导航中，平行线与垂直线的使用可以确定航线和方位。

综上所述，平行线与垂直线是几何学中的重要概念，具有各自的定义、判定方法和性质。

平行线与垂直线的认识知识点总结平行线和垂直线是几何学中常见的两种线性关系，它们在我们的日常生活和数学研究中都起到重要的作用。

本文将对平行线和垂直线的概念、性质和应用进行总结，以帮助读者更好地理解和运用这两种线性关系。

一、平行线的概念和性质1. 平行线的定义：两条直线在平面内不相交，并且它们的所有点到另一直线的距离相等，则称这两条直线为平行线。

2. 平行线的判定：有以下几种方法可以判定两条直线是否平行：- 通过观察直线的方程是否满足平行线的定义；- 通过观察直线的斜率是否相等；- 通过观察直线的平行关系是否可以推导出等比例关系。

3. 平行线的性质：- 平行线之间不存在交点；- 平行线的斜率相等；- 平行线的夹角为180度；- 平行线之间的距离在平面上保持不变。

二、垂直线的概念和性质1. 垂直线的定义：两条直线相交，且相交的角度为90度，则称这两条直线为垂直线。

2. 垂直线的判定：有以下几种方法可以判定两条直线是否垂直：- 通过观察直线的方程是否满足垂直线的定义；- 通过观察直线的斜率之积是否为-1；- 通过观察直线之间的角度是否为90度。

3. 垂直线的性质：- 垂直线之间存在交点；- 垂直线的斜率之积为-1；- 垂直线之间的角度为90度；- 垂直线的斜率为正无穷和负无穷。

三、平行线和垂直线的应用1. 平行线的应用：- 在建筑设计中，平行线的概念被广泛运用于保持建筑物的平衡和稳定性；- 在地理测量中，通过观察地平线和水平线的关系，可以判断两条线是否平行；- 在艺术创作中，平行线的运用可以帮助构建透视效果。

2. 垂直线的应用：- 在建筑施工中，垂直线的运用可以保证建筑物的结构稳定；- 在地理测量中，通过使用测量仪器可以确定地表的垂直线；- 在数学和物理实验中，垂直线的概念被广泛运用于实验数据的分析和计算。

总结起来，平行线和垂直线是几何学中重要的概念，它们在日常生活和学术研究中都起到了至关重要的作用。

通过对平行线和垂直线的概念、性质和应用的总结，希望读者能够更好地理解和运用这两种线性关系，进一步提升数学和几何学方面的知识和能力。

平行线和垂直线的关系知识点总结平行线和垂直线是几何学中最基本的概念之一，它们之间存在着重要的关系。

本文将对平行线和垂直线的定义、性质及相关定理进行总结。

一、平行线的定义与性质1. 定义：如果两条直线在同一个平面上，且它们没有任何交点，那么它们被称为平行线。

2. 性质：a. 平行线的斜率相等：对于两条平行线l₁和l₂，如果l₁的斜率等于k，则l₂的斜率也等于k。

b. 平行线的法向量相等：对于两条平行线l₁和l₂，如果l₁的法向量为n₁，则l₂的法向量也等于n₁。

二、垂直线的定义与性质1. 定义：如果两条直线在同一个平面上，且它们相交成直角（90度），那么它们被称为垂直线。

2. 性质：a. 垂直线的斜率互为相反数：对于两条垂直线l₁和l₂，如果l₁的斜率为k₁，则l₂的斜率为-k₁。

b. 垂直线的法向量互为相反数：对于两条垂直线l₁和l₂，如果l₁的法向量为n₁，则l₂的法向量为-n₁。

三、平行线与垂直线的相关定理1. 垂直线的判定定理：如果两条直线的斜率互为相反数，那么它们是垂直线。

证明：设直线l₁的斜率为k₁，直线l₂的斜率为k₂。

根据性质2a，如果k₁=-k₂，那么l₁和l₂是垂直线。

2. 平行线的判定定理：如果两条直线的斜率相等且不相交，那么它们是平行线。

证明：设直线l₁的斜率为k₁，直线l₂的斜率为k₂。

根据性质2a，如果k₁=k₂且l₁和l₂没有交点，那么l₁和l₂是平行线。

3. 平行线之间的性质定理：如果有一条直线与两条平行线相交，那么它与另一条平行线也相交，并且这两条相交的线段互相平行。

证明：设直线l与平行线l₁和l₂相交于点A和B。

根据性质1，线段AB与l₁平行，线段AB与l₂平行。

这表明l与l₁和l₂的交点在同一直线上，且l与l₁和l₂平行。

四、应用案例1. 平行线和垂直线的应用广泛，例如在建筑设计中，可以利用平行线和垂直线的性质制定合理的结构方案，确保建筑物的稳定性和美观性。

2. 在平面几何中，利用平行线和垂直线的性质可以解决许多几何问题，如求解直线的交点、证明直线与圆的关系等。

平行线与垂直线的认识与判断知识点总结一、平行线的定义与性质平行线是在同一个平面上且不相交的两条直线。

根据平行线的定义和性质，可以总结出以下知识点：1. 定理1：如果一条直线与两条平行线相交，那么这两条平行线之间的对应角相等。

2. 定理2：如果两条直线与一条平行线相交，那么与这两条直线对应的的两组内错角互补。

3. 定理3：如果两条平行线分别与一条直线相交，那么对应角相等，内错角互补。

4. 定理4：如果两条直线被一条平行线截断，那么截断线上的对应线段成比例。

二、垂直线的定义与性质垂直线是与另一条线段、线、平面或者其中一个副角成直角的线。

根据垂直线的定义和性质，可以总结出以下知识点：1. 定理1：如果两条直线相交且互相垂直，那么它们之间的角是直角。

2. 定理2：如果一条直线与另一条与之垂直的线交于一点，那么对于这两条直线上的任意两组内错角和对应角，它们的和都是直角。

三、平行线与垂直线的判断方法判断两条直线是否平行或垂直，可以根据以下方法进行：1. 判断平行线的方法：a) 观察是否有两条直线上的对应角相等或内错角互补，如果成立，则两条直线平行。

b) 如果两条直线的斜率相等，但不相交，则这两条直线平行。

c) 如果两条直线的法向量相等，则这两条直线平行。

2. 判断垂直线的方法：a) 观察是否有两条直线上的对应角和内错角的和为直角，如果成立，则两条直线垂直。

b) 如果两条直线的斜率互为相反数，且不相交，则这两条直线垂直。

c) 如果两条直线的斜率的乘积为-1，则这两条直线垂直。

四、应用举例下面以几个实例来应用平行线与垂直线的知识：例1：已知直线L1：y = 2x + 3，直线L2：y = -0.5x + 5。

判断L1和L2的关系。

解：通过观察可以发现，L1和L2的斜率互为相反数，且它们的直线方程不同，不相交。

所以根据判断垂直线的方法，可以判断L1和L2垂直。

例2：已知直线L1：y = 3x + 2，直线L2：y = 3x + 5。